

大模型系列:Flash Attention V2整体运作流程
描述
大家好,这就为您献上不知鸽了多久的Flash Attention V2原理解读。
在V1的讲解中,我们通过详细的图解和公式推导,一起学习了Flash Attention的整体运作流程。如果大家理解了V1的这块内容,就会发现V2的原理其实非常简单:无非是将V1计算逻辑中的内外循环相互交换,以此减少在shared memory上的读写次数,实现进一步提速。那当你交换了循环位置之后,在cuda层面就可以配套做一些并行计算优化。这就是V2的整体内容。
总结起来一句话:“交换了循环位置“,虽是短短一句话,却蕴含着深深的人生哲理:只要基座选得好,回回都有迭代点,年年勇破okr!
回归正题,本文也分两个部分进行讲解:原理与cuda层面的并行计算。
在阅读本文前,需要先阅读V1的讲解,本文会沿用V1的表达符号及推演思路。
一、Flash Attention V2整体运作流程
1.1 V1的运作流程
我们先快速回顾一下V1的运作流程:以K,V为外循环,Q为内循环。
,遍历:
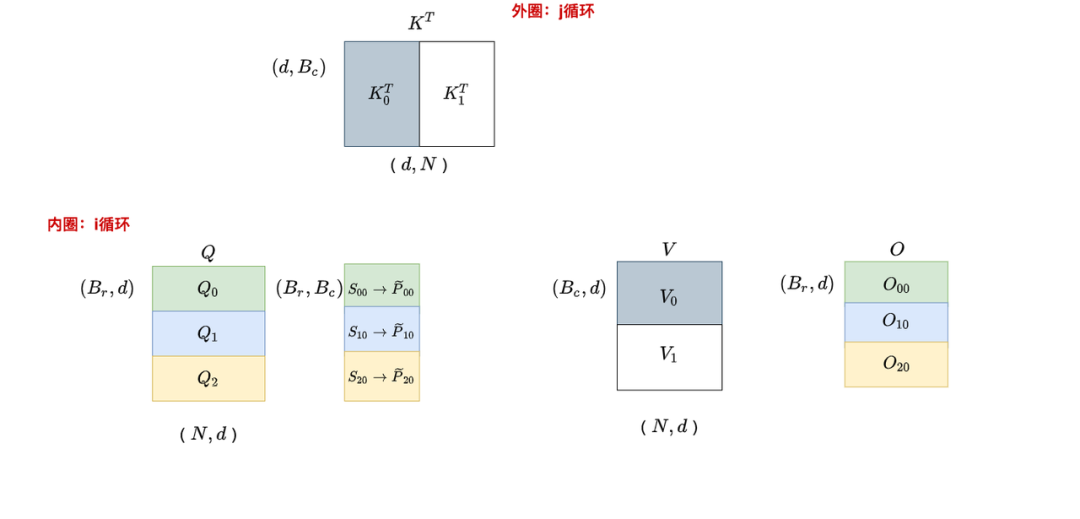
,遍历:
为了帮助大家更好理解v1中数据块的流转过程,在图中我们画了6块O。但实际上最终只有三块O:。
以为例,它可理解成是由经过某些处理后汇总而来的。进一步说,
我们在外循环j = 0时,先遍历一次所有的i,在这个阶段中我们产出,并将它和一些别的重要数据写回HBM中
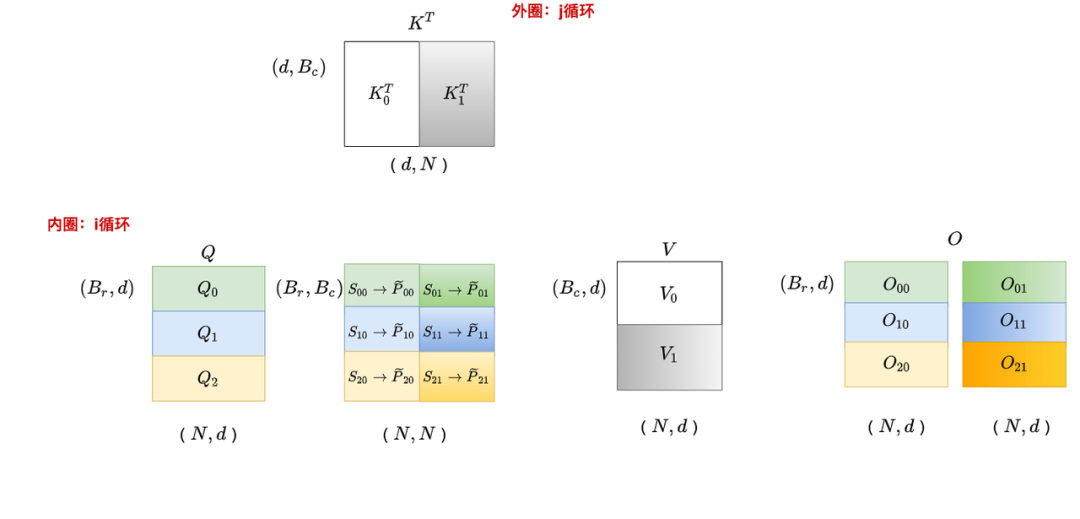
接下来我们进行第二次外循环,即j=1,在这个阶段中我们产出。同时我们把和那些重要的数据从HBM传入shared memory中,然后从shared memory中读取它们,以配合产出最终的
(关于如何得到的细节我们在V1讲解中详细推导过,这里不再赘述)
在这个过程中,你是不是隐隐觉得有些别扭:
其实都和有关系,那我为什么不以Q为外循环,以KV为内循环做遍历呢?这样我不就能避免往shared memory上读写中间结果,从而一次性把乃至最终的给算出来?
同时,softmax这个操作也是在row维度上的,所以我固定Q循环KV的方式,更天然符合softmax的特性。
1.2 V2的运作流程
基于1.1中的思想,我们在V2中将原本的内外循环置换了位置(示意图就不画了,基本可以对比V1示意图想象出来)。我们直接来看V2的伪代码(如果对以下伪代码符号表示或解读有疑惑的朋友,最好先看一下V1的讲解)。
(1)V2 FWD

现在,想象自己固定住了一块Q(i),依此循环K和V的分块(j),在这个想象下我们来解读这份FWD为代码。
第8行,计算分块
第9行:
表示截止到当前分块(包含当前分块)为止的rowmax
表示使用当前每行最大值计算归一化前的(我们在V1中说过,不带波浪号的P表示(s-rowmax)/rowsum的结果,带波浪号表示(s-rowmax))
表示截止到当前分块(包含当前分块为止)的rowsum
第10行:表示截止到当前分块(包含当前分块)为止计算出的O值。由第9和第10行知,当我们固定Q循环KV时,我们每个分块都是用当前最新的rowmax和rowsum计算的,同理对应的也是用当前最新的rowmax和rowsum计算的。这样当我们遍历完所有的KV时,得到的就等于最终全局的结果。相关的证明我们在V1讲解中给过,这里不再赘述,只额外提两点:
可能在有些朋友下载的V2论文中,第十行这里O前面的因子项是,这个公式应该是错误的(大家动手推一下就可知,初次看到时让我困扰了很久)。在作者个人主页的论文链接中,这个typo已经被修正。
你可能已发现这个O的计算中缺少归一化的一项,这一项其实放到了第12行做统一计算。这也是V2优化的一个点:尽量减少非矩阵的计算,因为在GPU中,非矩阵计算比矩阵计算慢16倍。
比起V1,V2中不用再存每一Q分块对应的和了。但是在BWD的过程中,我们仍需要来做和的重计算,这样才能用链式求导法则把dQ,dK,dV正常算出来。V2在这里用了一个很巧妙的方法,它只存一个东西(代码13行,这样又能进一步减少shared memory的读写):,这个等式中小写的m和l可以理解成是全局的rowmax和rowsum。在接下来BWD的讲解中,我们会来看到这一项的妙用。
(2)V2 BWD
一个建议:如果你在阅读本节中觉得很困惑,一定记得先去看V1的BWD部分,有非常详细的推导介绍。看完再来看本节就很顺畅了。

我们观察到,在V2 BWD中,内外循环的位置又换回来了,即还是KV外循环,Q内循环,这是为什么呢?
我们知道在BWD的过程中,我们主要是求(为了求它们还需要求中间结果,我们来总结一下这些梯度都需要沿着哪些方向AllReduce:
:沿着i方向做AllReduce,也就是需要每行的结果加总
:沿着i方向做AllReduce,也就是需要每行的结果加总
:沿着j方向做AllReduce,也就是需要每列的结果加总
:只与当前i,j相关
基于此,如果你还是保持Q外循环,KV外循环不变的话,这种操作其实是固定行,遍历列的,那么在这些梯度中,只有从中受益了,K和V的梯度则进入了别扭的循环(也意味着要往shared memory上写更多的中间结果);但如果你采用KV外循环,Q内循环,这样K和V都受益,只有Q独自别扭,因此是一种更好的选择。(S和P的计算不受循环变动影响)。
前面说过,在BWD过程中读写我们要用全局的重新计算,计算公式如下:
但如此一来,我们就要从shared memory上同时读取,似乎有点消耗读写。所以在V2中,我们只存储,然后计算:
很容易发现这两个计算是等价的,但V2的做法节省了读写量
好,现在我们就把V2相对于V1在计算原理上的改进介绍完了。接下来我们总结一下V2相对于V1所有的改进点。
二、V2相对V1的改进点
之所以把这块内容放到“V2整体流程介绍”之后,是想让大家在先理解V2是怎么做的基础上,更好体会V2的优点。
总体来说,V2从以下三个方面做了改进:
置换内外循环位置,同时减少非矩阵的计算量。(这两点我们在第一部分中已给出详细说明)
优化Attention部分thread blocks的并行化计算,新增seq_len维度的并行,使SM的利用率尽量打满。这其实也是内外循环置换这个总体思想配套的改进措施
优化thread blocks内部warp级别的工作模式,尽量减少warp间的通讯和读取shared memory的次数。
第二和第三点都可以归结为是cuda gemm层面的优化,我们马上来细看这两点。
三、V2中的thread blocks排布
// gridDim in V1 // params.b = batch_size, params.h = num_heads dim3 grid(params.b, params.h); // gridDim in V2 const int num_m_block = (params.seqlen_q + Kernel_traits::kBlockM - 1) / Kernel_traits::kBlockM; dim3 grid(num_m_block, params.b, params.h);
这段代码整合自flash attention github下的cutlass实现,为了方便讲解做了一点改写。
这段代码告诉我们:
在V1中,我们是按batch_size和num_heads来划分block的,也就是说一共有batch_size * num_heads个block,每个block负责计算O矩阵的一部分
在V2中,我们是按batch_size,num_heads和num_m_block来划分block的,其中num_m_block可理解成是沿着Q矩阵行方向做的切分。例如Q矩阵行方向长度为seqlen_q(其实就是我们熟悉的输入序列长度seq_len,也就是图例中的N),我们将其划分成num_m_block份,每份长度为kBlockM(也就是每份维护kBlockM个token)。这样就一共有batch_size * num_heads * num_m_block个block,每个block负责计算矩阵O的一部分。
为什么相比于V1,V2在划分thread block时,要新增Q的seq_len维度上的划分呢?
先说结论,这样做的目的是尽量让SM打满。我们知道block是会被发去SM上执行的。以1块A100 GPU为例,它有108个SM,如果此时我们的block数量比较大(例如论文中所说>=80时),我们就认为GPU的计算资源得到了很好的利用。现在回到我们的输入数据上来,当batch_size和num_heads都比较大时,block也比较多,此时SM利用率比较高。但是如果我们的数据seq_len比较长,此时往往对应着较小的batch_size和num_heads,这是就会有SM在空转了。而为了解决这个问题,我们就可以引入在Q的seq_len上的划分。
看到这里你可能还是有点懵,没关系,我们通过图解的方式,来一起看看V1和V2上的thread block到底长什么样。
3.1 V1 thread block
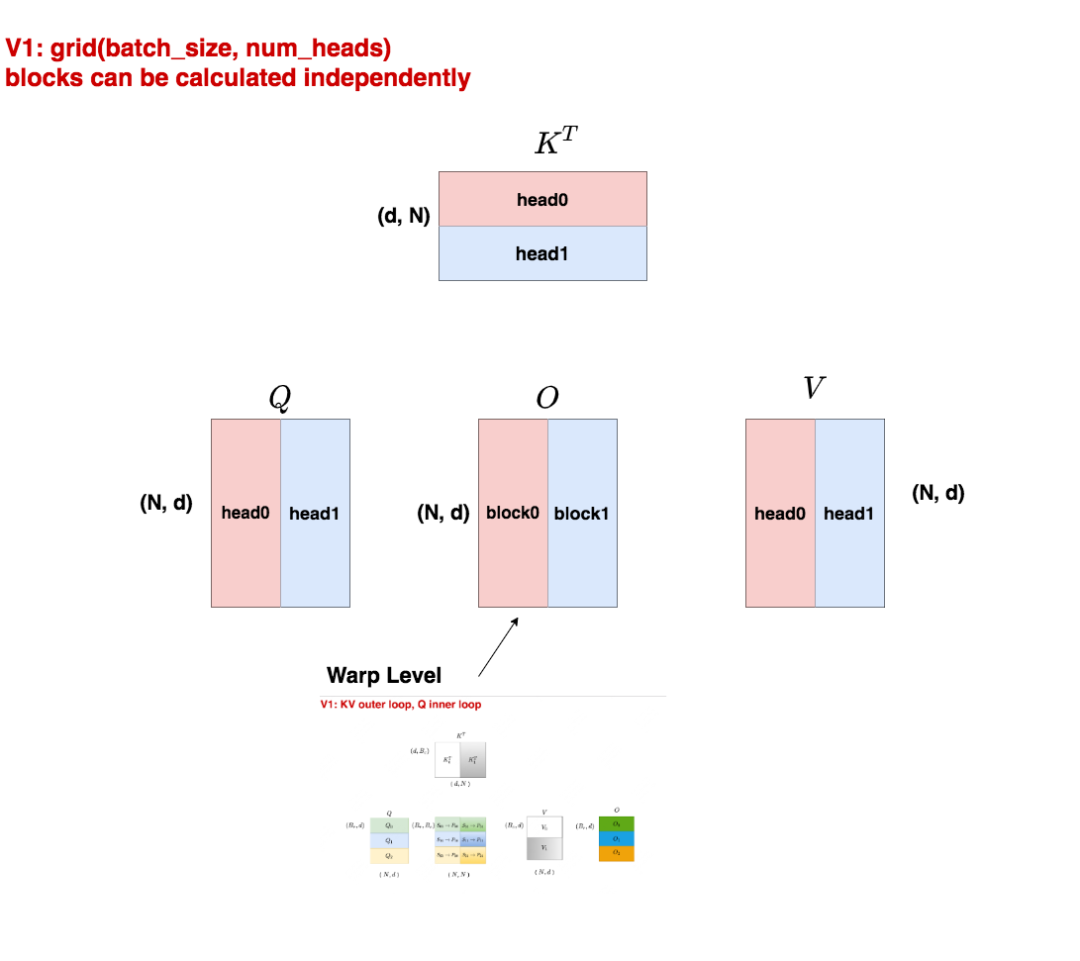
假设batch_size = 1,num_heads = 2,我们用不同的颜色来表示不同的head。
我们知道在Multihead Attention中,各个head是可以独立进行计算的,在计算完毕后将结果拼接起来即可。所以我们将1个head划分给1个block,这样就能实现block间的并行计算,如此每个block只要在计算完毕后把结果写入自己所维护的O的对应位置即可。
而每个block内,就能执行V1中的"KV外循环,Q内循环”的过程了,这个过程是由block的再下级warp level层面进行组织,thread实行计算的。这块我们放在第四部分中讲解。
3.2 V2 thread block
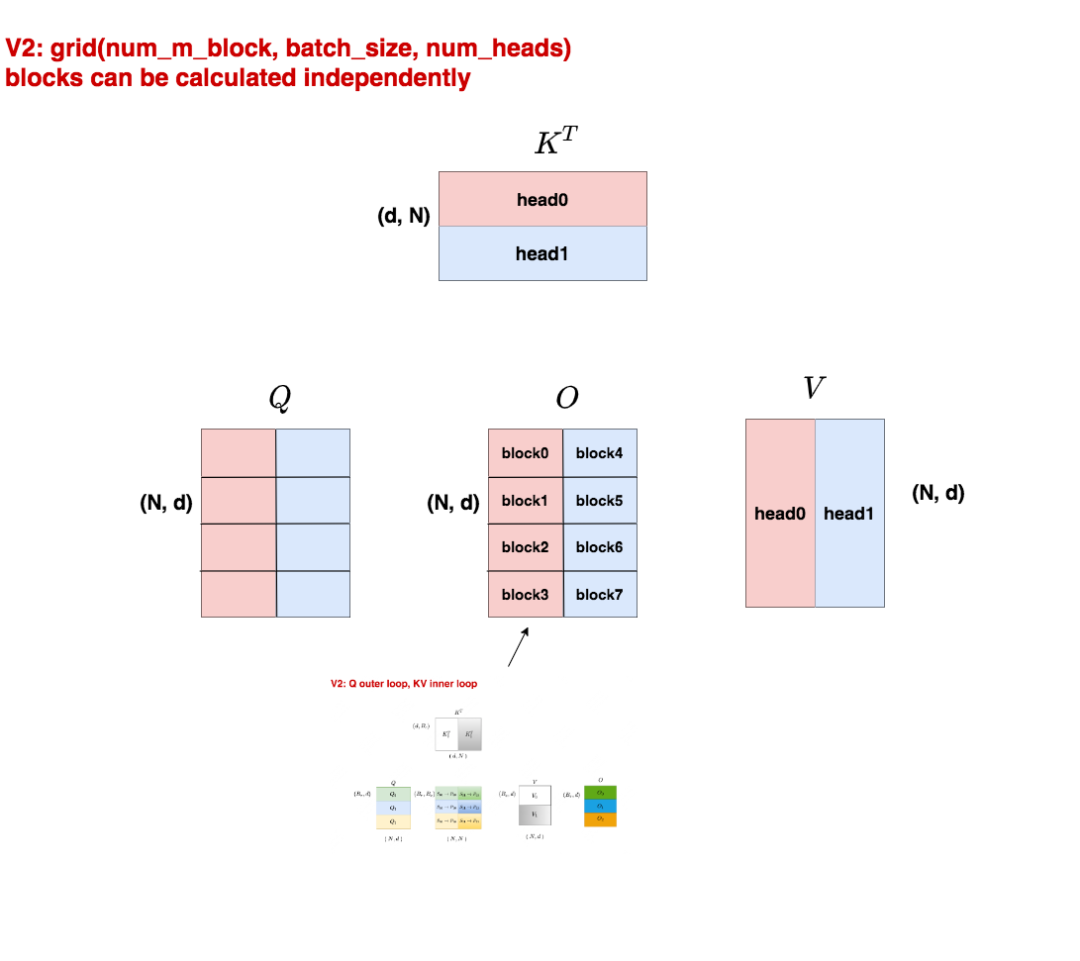
现在我们继续假设batch_size = 1,num_heads = 2。
与V1不同的是,我们在Q的seq_len维度上也做了切分,将其分成四份,即num_m_block = 4。所以现在我们共有124 = 8个block在跑。这些block之间的运算也是独立的,因为:
head的计算是独立的,所以红色block和蓝色block互不干扰
采用Q做外循环,KV做内循环时,行与行之间的block是独立的,因此不同行的block互相不干扰。
每个block从Q上加载对应位置的切块,同时从KV上加载head0的切块,计算出自己所维护的那部分O,然后写入O的对应位置。
在这里你可能想问,为什么只对Q的seq_len做了切分,而不对KV的seq_len做切分呢?
在V2的cutlass实现中,确实也提供了对KV的seq_len做切分的方法。但除非你认为SM真得打不满,否则尽量不要在KV维度上做切分,因为如此一来,不同的block之间是没法独立计算的(比如对于O的某一行,它的各个部分来自不同的block,为了得到全局的softmax结果,这些block的结果还需要汇总做一次计算)。
3.3 seq parallel不是V2特有
如果你看过V1的代码,你会发现,其实在V1后期的版本中,也出现了seq维度的并行:
// V1 seq parallel: csrc/flash_attn/src/fmha_fwd_launch_template.h
dim3 grid(launch_params.params.b, launch_params.params.h, launch_params.params.num_splits);
// nums_splits计算方法
// Find the number of splits that maximizes the occupancy. For example, if we have
// batch * n_heads = 48 and we have 108 SMs, having 2 splits (efficiency = 0.89) is
// better than having 3 splits (efficiency = 0.67). However, we also don't want too many
// splits as that would incur more HBM reads/writes.
// So we find the best efficiency, then find the smallest number of splits that gets 95%
// of the best efficiency.
// [2022-11-25] TD: Mark this as "inline" otherwise we get "multiple definition" error.
inline int num_splits_heuristic_fwd(int batch_nheads, int num_SMs, int ctas_per_sm, int max_splits) {
float max_efficiency = 0.f;
std::vector efficiency;
efficiency.reserve(max_splits);
for (int num_splits = 1; num_splits <= max_splits; num_splits++) {
float n_waves = float(batch_nheads * num_splits) / (num_SMs * ctas_per_sm);
float eff = n_waves / ceil(n_waves);
// printf("num_splits = %d, eff = %f
", num_splits, eff);
if (eff > max_efficiency) { max_efficiency = eff; }
efficiency.push_back(eff);
}
for (int num_splits = 1; num_splits <= max_splits; num_splits++) {
if (efficiency[num_splits - 1] > 0.95 * max_efficiency) {
// printf("num_splits chosen = %d
", num_splits);
return num_splits;
}
}
return 1;
}
....
// 可以发现num_splits也是由Q的seq_len维度切分来的
launch_params.params.num_splits = num_splits_heuristic_fwd(
launch_params.params.b * launch_params.params.h, dprops->multiProcessorCount,
ctas_per_sm,
/*max_splits=*/std::min(30, (launch_params.params.seqlen_q + M - 1 / M))
);
上图代码中的num_splits也是在由Q的seq_len维度切分来的。通过这段代码,我猜想作者在V1后期引入seq_len维度切分的原因是:V1也需要解决seq_len过长时,batch_size和num_heads较小而造成SM打不满的问题。
num_splits_heuristic_fwd这个函数的作用概括起来就是,我先提供一连串num_splits值的备选,然后由这个函数计算出每个备选值下SM的利用率。计算完之后,我先找到最高的利用率,然后再找出满足利用率>=0.95 * max(利用率)的那个最小的num_split值,作为最终的选择。
细心的你此时可能已经观察到了,虽然V1也引进过seq parallel,但是它的grid组织形式时(batch_size, num_heads, num_m_blocks),但V2的组织形式是(num_m_blocks, batch_size, num_heads),这种顺序调换的意义是什么呢?
直接说结论,这样的调换是为了提升L2 cache hit rate。大家可以看下3.2中的图(虽然block实际执行时不一定按照图中的序号),对于同一列的block,它们读的是KV的相同部分,因此同一列block在读取数据时,有很大概率可以直接从L2 cache上读到自己要的数据(别的block之前取过的)。
3.4 FWD和BWD过程中的thread block划分
在3.1~3.3中,我们其实给出的是FWD过程中thread block的划分方式,我们知道V2中FWD和BWD的内外循环不一致,所以对应来说,thread block的划分也会有所不同,我们详细来看:

在图中:
worker表示thread block,不同的thread block用不同颜色表示
整个大方框表示输出矩阵O
我们先看左图,它表示FWD下thread block的结构。每一行都有一个worker,它表示O矩阵的每一行都是由一个thread block计算出来的(假设num_heads = 1),这就对应到我们3.1~3.3中说的划分方式。那么白色的部分表示什么呢?我们知道如果采用的是casual attention,那么有一部分是会被mask掉的,所以这里用白色来表示。但这不意味着thread block不需要加载白色部分数据对应的KV块,只是说在计算的过程中它们会因被mask掉而免于计算(论文中的casual mask一节有提过)。
我们再看右图,它表示BWD下thread block的结构,每一列对应一个worker,这是因为BWD中我们是KV做外循环,Q做内循环,这种情况下dK, dV都是按行累加的,而dQ是按列累加的,少数服从多数,因此这里thread_block是按的列划分的。
四、Warp级别并行
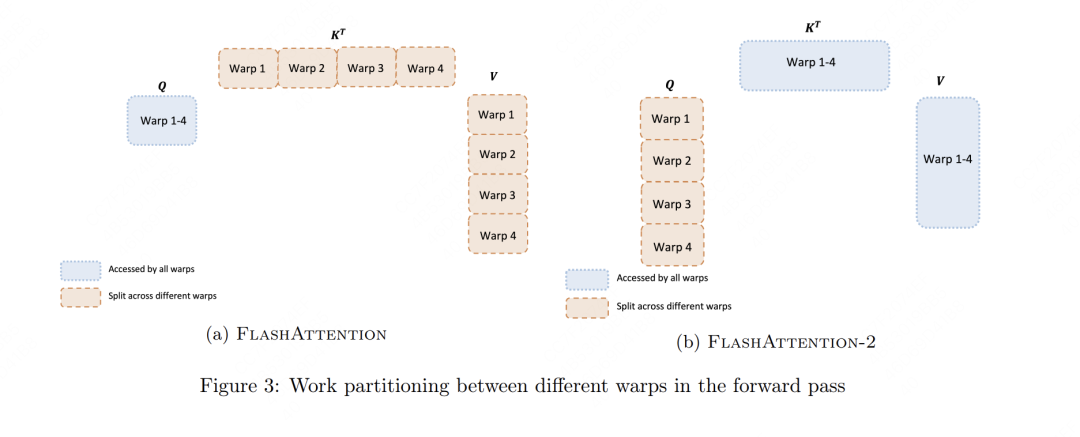
讲完了thread block,我们就可以再下一级,看到warp level级别的并行了。左图表示V1,右图表示V2。不管是V1还是V2,在Ampere架构下,每个block内进一步被划分为4个warp,在Hopper架构下则是8个warp。
在左图(V1)中,每个warp都从shared memory上读取相同的Q块以及自己所负责计算的KV块。在V1中,每个warp只是计算出了列方向上的结果,这些列方向上的结果必须汇总起来,才能得到最终O矩阵行方向上的对应结果。所以每个warp需要把自己算出来的中间结果写到shared memory上,再由一个warp(例如warp1)进行统一的整合。所以各个warp间需要通讯、需要写中间结果,这就影响了计算效率。
在左图(V2)中,每个warp都从shared memory上读取相同的KV块以及自己所负责计算的Q块。在V2中,行方向上的计算是完全独立的,即每个warp把自己计算出的结果写到O的对应位置即可,warp间不需要再做通讯,通过这种方式提升了计算效率。不过这种warp并行方式在V2的BWD过程中就有缺陷了:由于bwd中dK和dV是在行方向上的AllReduce,所以这种切分方式会导致warp间需要通讯。
针对V2 warp切分影响BWD这点,作者在论文中依然给出了“BWD过程相比V1也有提升”的结论,针对这点,我在github issue上找到了一条作者的回复(在“安装报错”组成的issue海洋里捞出的宝贵一条):
最关键的可能是第1和第2点,关于第1点,我想作者应该是说,之前需要反复读取KV的数据,现在只用反复读取Q的数据,因此从一定程度上节省了shared memory的读写次数。第2点理解起来有点复杂,个人觉得是将warp处理的tile划分得更像方形。这样做的好处是在做casual mask的时候可以方便写代码大块丢掉被mask掉的tile(见论文casual masking部分),进一步加速计算。第3点是关于一些底层的优化,就不提了。
好!关于V2我们就介绍到这了,写这篇文章的时候,我刚粗过了一遍triton的flash attention实现,以及扫了一下cutlass实现的入口。如果后续有时间,我会出一些源码解读的文章(从cuda gemm -> triton gemm -> triton flash attention,看,又给自己挖了一个坑)。如果出不了,那一定不是我鸽人,那肯定是我不会(没错,就是这样)。
审核编辑:黄飞
-
RDMA over RoCE V2设计2:ip 整体设计考虑2025-07-16 564
-
微软OmniParser V2:大模型转化为计算机智能体2025-02-18 2720
-
产品简介 | RZ/V2系列MPU2024-05-08 1383
-
Cadence 与 Arm 合作,成功利用 Cadence AI 驱动流程加速 Neoverse V2 数据中心设计2023-09-05 4411
-
智能电源模块,Motion SPM® 55 V2 系列用户指南2022-11-15 577
-
V2 控制器的操作原理2022-11-14 621
-
国民技术DS_N32WB452系列数据手册V22022-10-18 555
-
NodeMCU V2 Amica V3 Lolin的盾牌2022-08-24 732
-
智能BMS V2开源设计2022-08-08 1878
-
LED面板V2开源分享2022-08-02 585
-
学习V2更新板开源分享2022-07-26 511
-
Kinect v2(Microsoft Kinect for Windows v2 )配置移动电源解决方案2022-01-05 789
-
ST-LINK/V2 ST-LINK/V2ST-LINK / V2在调试器/编程器STM8和STM322020-05-21 1921
-
我可以使用ST-LINK/V2为STM8S系列编程闪存吗?2018-09-17 4395
全部0条评论

快来发表一下你的评论吧 !

