

量子世界能否被经典计算机所模拟?
描述
原文作者:张天蓉
经典计算机无法模拟量子力学,那就建造一个按照量子力学规律运行的计算机来直接模拟和计算量子世界。
你肯定见过上面这张著名的照片,在29人中有17位诺奖得主,包括爱因斯坦、玻尔、居里夫人等,被称为是科学史上最牛的合照,照片中的大多数人物对量子力学做出了重要贡献。
灵魂人物费曼
那是在1981年,历经了80年风雨的量子理论已经是一门成熟又成功的物理理论。尽管玻尔和爱因斯坦世纪之争的余波犹存,量子学者们仍旧在孜孜不倦地探究更好的理论诠释,但是,1964年贝尔不等式的提出,以及之后多次实验验证贝尔不等式不成立的事实,已经足以证实量子论的正确,叠加态的存在,量子纠缠的存在。量子物理的实际应用更是无处不在,它曾经直接奠定了原子弹、核技术、光学、半导体等的理论基础,让人类赢得了战争,给社会带来了伟大的技术革命。特别是以量子力学为基础的半导体物理及其应用,促成了晶体管和集成电路两项伟大的发明,使计算机技术在1970年代急速发展,如日中天。
那年的五月,美国波士顿MIT的校园里,鲜花盛开,绿草如茵。历史悠久的恩迪科特大厦,正在进行为期三天的热烈讨论。大约 50 位科学家聚集在一起,召开了物理学中的“量子”,和计算机技术的第一次“联姻”会议,从此揭开了研究发展量子计算机的新篇章[1]。
量子和计算,两者听起来似乎风马牛不相及,为何要“联姻”呢?
当然,其实两者本来就有关,如前所述,没有量子力学作为理论基础,不可能有半导体工业,也就没有晶体管,没有集成电路,没有如此发达的计算机产业。不过,这一次科学家们所提及的,是实质上的联姻,是要让计算机按照量子力学不同寻常的奇妙规律和方式来工作,来进行计算!
这次会议并不是由费曼召集或主持的,但费曼(在照片中标号为38)无疑地成为了那几天讨论的主角,会议的灵魂人物。这是由费曼无限的个人魅力形成的。费曼何许人也!他既是家喻户晓的伟大科学家,又是极棒的演员和超群的教师。是他眉飞色舞的演讲,将物理和计算机专家们的眼光汇聚到一起;是他精彩的辩论,让与会人士深入理解了大会的主题:计算科学还有瑕疵,但也许能“吸取量子现象的运作方式”而从中受益。
费曼1918年生于纽约一个犹太人家庭。不同于一般理论物理学家在人们心目中的严谨刻板形象,费曼被人誉为“一个智慧超凡的科学鬼才”,其传奇故事脍炙人口。他从小就是个科学顽童,后来不仅是著名的物理学家,也是一位开保险箱专家和经常演出的邦戈鼓手。此外,他还曾经像一位真正的画家一样卖掉过自己的好几幅绘画作品。他在MIT读完大学本科后,到普林斯顿大学读Ph.D.,师从约翰·惠勒。他参加了著名的曼哈顿计划,开创量子物理中路径积分的想法,建立了量子电动力学,被授予1965年的诺贝尔物理学奖。
除了量子之外,数学和计算,一直是费曼的乐趣所在。费曼曾经得过普特南数学竞赛第一名,在曼哈顿计划中,费曼负责了多项繁琐的计算任务,还曾将年轻人组织成“人肉计算机”,流水线般地完成编程式的计算步骤。
现代电子计算机的计算能力,引起了费曼的注意。他与同行们一起钻研用计算机模拟物理世界的方法,发现这个计算方法只适用于模拟经典的物理世界,对量子世界并不完全适用。
因此,费曼在会议上提出一个新颖的设问:经典计算机可以被用来模拟量子世界吗?答案是否定的 。因为在模拟量子现象时,经典计算机的计算量,将随着系统(粒子数N)的增大而指数增加。费曼认为微观世界的本质是量子的,N非常大,是传统计算机在有效时间内解决不了的问题。他紧接着就提出一个独特的设想:能不能发明出一个更新式的计算机,一个按照量子力学规律运行的计算机,以此直接模拟和计算量子世界?
“量子计算机”的概念,从此出现在人们的视野。
第一张“明星照”
我们再回头看看这张汇聚如此多的精英在同一张相框内的会议明星照。
这时候,距离第一张照片的1927年,已经过去了整整54年。不用仔细对照名字就能知道,两张照片中不太可能有重叠的人物。大半个世纪过去了,照片1中的量子力学第一代创始人,大都已经驾鹤西去,少数仅存者也到了耄耋之年:德布罗意将近90岁,狄拉克也在准备过80大寿。他们都不在MIT的照片里!
我们能找到的,对量子理论发展作出过重要贡献的知名人物,是弗里曼·戴森和约翰·惠勒,分别在照片中标号为1和12。这两位都可以算作是诺贝尔物理奖的“漏网之鱼”!戴森是生活在美国的英国人,著名的数学物理学家,戴森为量子电动力学的建立做出了决定性的贡献,以他命名的物理术语很多,如:戴森球、戴森树、戴森变换等。他后来一直是普林斯顿高等研究院的教授,直到2020年96岁高龄去世。惠勒是费曼(#38)的老师,现代物理学中有许多他创造的术语:量子泡沫、黑洞、虫洞等。1980年,惠勒刚从普林斯顿到奥斯丁大学,正值他提出“延迟选择双缝思想实验” 之时,该实验巧妙地体现了量子力学与传统实在观之间的巨大分歧,他后来有一句名言:“万物皆比特”!
照片中居然有一位大名鼎鼎的早期德国机械计算机发明家:康拉德·楚泽(#15)。但他生不逢时,在创造力最旺盛的年纪,碰到了第二次世界大战。他制造出了Z-1、Z-2、Z-3、Z-4等一系列计算机,他1941年研制的Z-3,使用二进制和继电器,是世界上第一个有图灵完全功能的,可编程的通用图灵机。战争时代的科学家难免悲剧命运,楚泽辛苦的研究和设计工作,被埋没于战火硝烟中。楚泽生于1910年,时年71岁,估计是照片中最年长者。
此外还有诸多量子界的、计算机领域的专家和后起之秀:列昂尼德·莱文(43)、诺曼·帕卡德(4)、 阿瑟·伯克斯(35)、大卫·莱因韦伯(14)、 卡尔·亚当·佩特里(17)、爱德华·弗雷德金(9)、汤姆·托弗里(10)、罗尔夫·兰道尔(11)、保罗·贝尼奥夫(30)、丹尼·希利斯(34) ……还有查尔斯·贝内特,是拍照片的人,所以不在框内。
如今又是43年过去了,一代又一代的精英不断涌现,众多分支的物理学家、计算机科学家,都在量子计算的发展中,留下了他们的身影!虽然尚未迎来量子计算的春天,但黑暗渐消曙光微现。况且,科学之精神重在过程,科学家群星们的努力探索,值得记载和传承。
因为:前人之经验,后人可为鉴。
费曼提出的问题
那么,费曼到底提出了什么问题呢?
也许你会感到奇怪,计算机的能力已经如此强大,为什么还要研发量子计算机呢?是科学家们别出心裁多此一举吧?其实是因为经典计算技术中,有一个难以解决的“复杂度”问题。
我们经常说到保密通讯的密码,什么样的密码才是最安全的?当然应该是计算机破译不了的,或者是说得更准确一些:是计算机在有效的时间内破译不了的。所谓有效的时间,也就是足够短的时间。你想想,在战争中,总不能花上几年的时间来破解一条敌军传递的信息吧。不要说几年,几天也太慢了啊。这就是说,这类问题的时间“复杂度”太大了。
“复杂度”表征的是所需计算量与问题涉及系统变量数N之间的关系。复杂度分时间和空间,时间复杂度指的是所需计算时间T与系统变量数N之间的关系;空间复杂度指所需比特数B与N之间的关系。两者实际上互相关联,我们以时间复杂度为例。
一般来说,计算时间将随着系统增大而增加。但T的增大因问题而异,T与N可以成线性关系,也可能成平方关系,也有可能是随着N指数增长。可以用函数 O(1)、O(N)等等来表示复杂度,即表示T随N增加的快慢。
时间复杂度包括:线性关系O(N)、平方关系O(N2)、立方关系O(N3)等等,最困难的是指数关系:例如O(2N)[2],见图4。
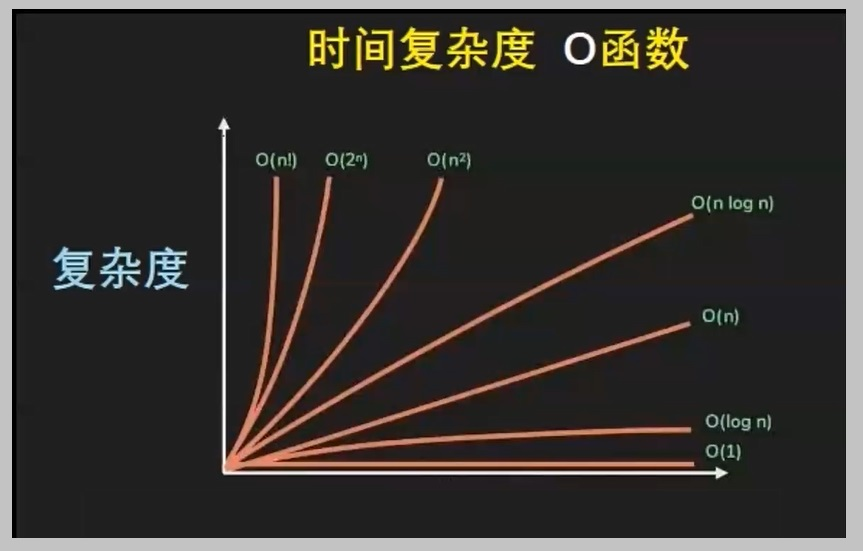
图4 不同问题的不同复杂度
需要注意的是,复杂度指的是,计算时间随着参数大小变化的规律,并不是具体计算的实际时间。所以复杂度对应于计算机的“计算方式”,即计算机的类型,而非“速度快慢”。举例来说吧,要破解某条指数关系密码,1944年的机器计算时间是30年,1980年的机器只需10年,2020年需9年,但它们都是经典计算机,复杂度是一样的,有限的方式提高速度,改变不了复杂度。
这也就是费曼说的,经典计算机无法模拟量子力学的原因。那么,既然经典的计算机不行,是否有其他的计算模式可以模拟量子世界呢?费曼的想法别出一格,却又合情合理:他认为微观世界的本质是量子的,想要模拟它,就得用和自然界的工作原理一样的方式,也就是量子的方式才行。对此,费曼风趣地表示,既然这个该死的大自然不是经典的,你最好是“模拟它的方法来模拟它”,以其人之道,还治其人之身嘛!我们得做到和大自然做的一模一样。那就是说,我们要想模拟这个量子行为的世界,就得研究微观世界的量子是如何工作的,然后,建造一个按照量子力学的规律来运行的计算机,最后才能模拟它。不过,费曼最后又感叹地说:“天哪,这是一个非常精彩的问题,但却不是那么容易解决的!”
量子比特vs经典比特
量子计算的方法与经典计算是完全不同的,两类计算机速度差异的原因是来自于量子现象和经典现象物理规律的不同。量子计算基于量子规律。量子规律的精髓是什么?其实可以用一句话来概括:种种奇怪的量子现象都是来自于量子“叠加态”[3]。
你也许听过最奇怪的量子现象是“纠缠态”和双缝实验,不过实际上,纠缠态也是一种叠加态,是多粒子体系状态叠加产生的效应,而各类“诡异”的双缝实验均可用叠加态解释。
什么是叠加态呢?根据我们的日常经验,一个物体在某一时刻总会处于某个固定的状态。状态可以用位置、速度、相位、能量等物理参数表示。比如我说,我现在在客厅里,或者说,我现在在房间里。要么在客厅要么在房间,这两种位置状态必居其一。然而,在微观的量子世界中,情况却有所不同!微观粒子可以处于一种不确定的状态中。例如电子可以同时位于两个(甚至多个)不同的地点。也就是说,电子既在A又在B,电子的状态是“A”和“B”两种状态按一定概率的叠加,物理学家们把电子的这种混合状态叫做叠加态。
经典世界中的“波”可以是叠加态,但经典“粒子”(宏观物体)不存在叠加态。比如说,我此时此刻不可能既在客厅又在房间;一只猫要么是死猫要么是活猫,不存在“既死又活”的猫!
微观量子世界的粒子一般都处于“叠加态”,但是我们却观测不到叠加态!原因是因为“观察测量”的宏观行为将引起所谓“波函数塌缩”或者被诠释为“退相干效应”,即观测之前是叠加态,观测之后叠加态不复存在,“坍缩” 成了一个确定的状态!因此,我们只能“以某种概率“观测到叠加的多个本征态之一。例如,如果盒子中的”薛定谔猫“化身微观粒子,它的状态可以被表示成“死猫”与“活猫”的叠加态(如图5)。
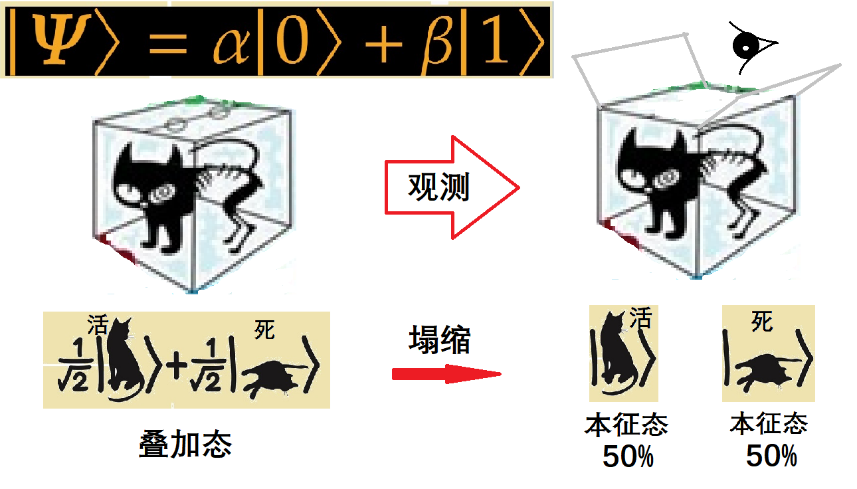
图5 叠加态和坍缩
然而,只要你打开盒子观测,叠加态就塌缩了!你有50%的可能性看到“活猫”,50%的可能性看到“死猫”,但你看不到“既死又活”的猫,换言之,你观测不到它们的叠加态!
有时稍微加点数学抽象,更能理解叠加态。因为事实上经典的宏观物体(比如猫)是没有叠加态的,完全不用数学便只想到宏观的直观经验,总是试图用经典概念来理解“叠加态”,这种经典现象又是不可能的。因此可以说,不放弃经典,永远不可能真懂叠加态!所以,我们最好记住图5左上角那个叠加态波函数的公式,也就是:|y> = a|0> + b|1>。
叠加态通常用2分量量子系统来表示,上面公式中的|0>和|1>是系统的两个本征态。
费曼正是因为对量子理论,对叠加态的深入理解,才能提出量子计算技术的设想。
审核编辑:黄飞
-
【《计算》阅读体验】量子计算2024-07-13 873
-
【量子计算机重构未来 | 阅读体验】+ 了解量子叠加原理2024-03-13 4962
-
【量子计算机重构未来 | 阅读体验】+量子计算机的原理究竟是什么以及有哪些应用2024-03-11 4769
-
【量子计算机重构未来 | 阅读体验】+ 初识量子计算机2024-03-05 753
-
量子计算机的作用有哪些2023-12-30 3531
-
什么是后量子密码学?量子计算机vs经典计算机2023-12-19 2982
-
量子是个啥?量子计算机有啥用?2021-07-27 2260
-
微软进军量子计算机,即将发布量子计算机模拟器2019-12-05 3274
-
量子计算机原理_量子计算机有多强大2017-11-28 16410
-
什么是量子计算机?量子计算机的诞生,人类是否有望被模拟出来?2017-05-19 2660
-
中科院宣布已成功研制世界首台“超越经典”量子计算机2017-05-05 1146
-
量子计算机是什么?世界上第一台超越早期经典计算机,中国量子计算机诞生2017-05-04 3244
-
量子计算机或将提前实现2016-06-13 3347
全部0条评论

快来发表一下你的评论吧 !

