

单边低噪声放大器设计方案
描述
在接收器应用中,信号链中的第一个放大器对整个系统的噪声性能起着主导作用。该放大器应表现出尽可能低的噪声系数,同时提供可接受的高功率增益。因此,该低噪声放大器(LNA)的设计过程中应同时考虑增益和噪声性能。
在本文中,我们将了解如何根据这些要求设计单边 LNA。首先,我们将探讨如何在RF应用中指定双端口网络的噪声参数,然后设计一个同时实现特定增益和特定噪声水平的单边放大器。
双端口网络噪声参数
正如我在关于噪声系数指标的文章中详细讨论的那样,电路的输出噪声在很大程度上取决于其源阻抗。同时,连接到源导纳YS = GS + jBS的晶体管的噪声系数(F)由以下方程给出:
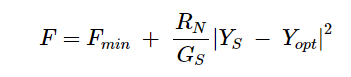
(1)
其中:
Fmin 是器件的最小噪声系数
RN 是器件的等效噪声电阻
Yopt 是最佳源导纳
GS 是源导纳YS的实部
从这个方程可以看出噪声因数(F)如何随着源导纳(YS)的变化而变化。观察到当YS = Yopt时,噪声系数减小到其最小值Fmin。
晶体管的量 Fmin、RN 和 Yopt 称为其噪声参数。我们不计算这些参数,而是由制造商提供或通过测量获得。Fmin 有时以 dB 形式表示为 NFmin,它随着晶体管的偏置点、温度和工作频率而变化。参数 RN 是一个敏感性因子,显示了当源导纳偏离 Yopt 时噪声系数增加的速度。
在低频时,Yopt是实数,但对于大多数有源器件,在50到100 MHz以上,它变为复数值。对于任何给定的双端口网络,我们可以找到一个Yopt值,使噪声因数最小化。请注意,方程式中没有S参数。事实上,器件的S参数并不提供有关其噪声性能的任何信息。
如前所述,F是噪声因数,以线性形式表示。噪声指数,简称NF,是将噪声系数转换为分贝表示的值。因此,F和NF之间的关系可以表示为:
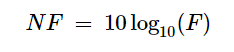
(2)
在实践中,确定噪声系数与源阻抗的依赖关系需要专门的噪声测量设备。这种设备使用支路调谐器向器件施加一系列复杂阻抗,并对这些测量结果进行分析,以在ΓS平面上生成等NF圆。
图1显示了一个假设设备的等NF圆。我们很快将更详细地讨论,这些圆。
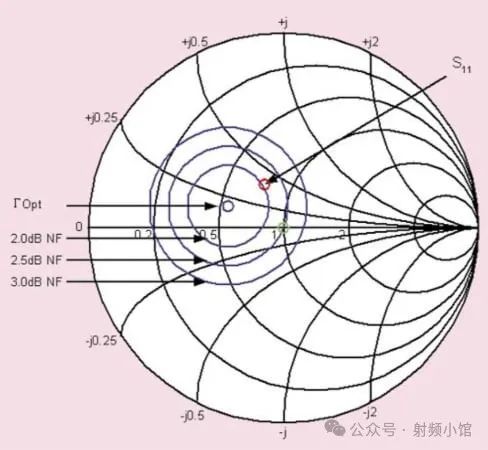
图1
请注意,常见的噪声系数分析仪和网络分析仪无法生成这些等噪声系数圆。
噪声系数另一种表达方式
上面介绍的参数RN也可以指定为导纳项, GN=1/RN 。此外,可以通过指定等效最佳源阻抗(Zopt=1/Yopt)或其相关的最佳源反射系数(Γopt)来解决公式,而不是指定最佳导纳。参数Yopt和Γopt之间有以下关系式:
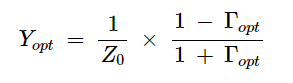
(3)
利用Γopt参数,方程1也可以表示为:
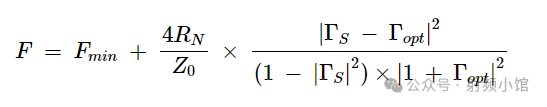
(4)
请注意,放大器的负载反射系数(ΓL)在公式4中并不出现。从这可以看出,输出匹配对噪声系数没有任何影响。然而,匹配的输出可以提供更多增益并减少后续级别的噪声影响。
一般来说,放大器的增益和噪声性能之间存在权衡——在最大增益处无法实现最小噪声。
绘制等 NF 圆
为了绘制给定的噪声系数(F)的NF圆,我们首先找到噪声系数参数(N)。这由以下公式给出:
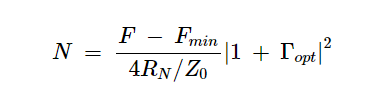
(5)
NF圆的中心(cF)由以下公式给出:
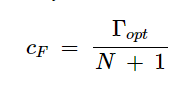
(6)
半径(rF):
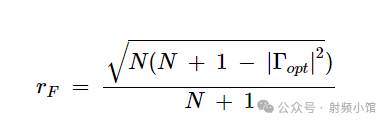
(7)
为了巩固这些概念,让我们通过一个例子来加深理解。
例子1:绘制噪声系数圆
假设对于具有以下S参数的晶体管,Z0 = 50 Ω,f = 1.4 GHz:
| f(GHz) | S11 | S21 | S12 | S22 |
| 1.4 | 0.533 ∠ 176.6° | 2.8 ∠ 64.5 ° | 0.02 ∠ 58.4 ° | 0.604 ∠ –58.3 ° |
该器件的噪声参数如下:
最小噪声系数(NFmin)= 1.6 dB
最佳源反射系数(Γopt)= 0.5 ∠ 130 度
等效噪声电阻(RN)= 20 Ω
让我们为这个晶体管在NF = 2 dB、2.5 dB 和 3 dB处绘制常数NF圆。表2总结了所需的计算。请注意,我们的方程使用F而不是NF,所以我们不能直接将噪声指数值插入方程中。相反,我们必须将它们从分贝测量转换为噪声系数所表示的线性项。
| NF | F | N | cF | rF |
| 2.0dB | 1.58 | 0.05 | 0.47 ∠ 130° | 0.20 |
| 2.5dB | 1.78 | 0.13 | 0.44 ∠ 130 ° | 0.30 |
| 3.0dB | 2.00 | 0.21 | 0.41 ∠ 130° | 0.37 |
噪声系数圆:
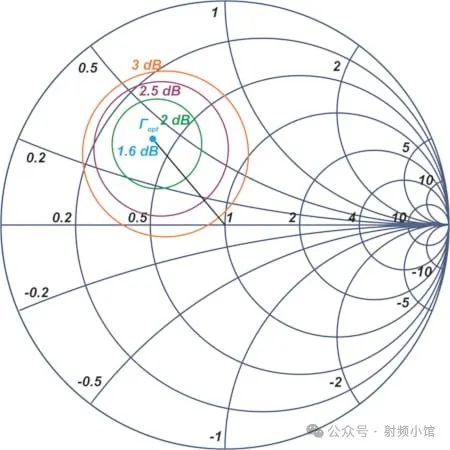
图2
请注意,噪声圆的中心位于从Smith图的中心到点Γopt的直线上(参见公式6)。在Γopt处,我们获得NFmin = 1.6 dB,噪声圆会变成一个单点。随着噪声指数的增加,圆的中心会向原点移动,其半径变大。
设计单边射频放大器以实现增益和噪声的平衡
NF圆被绘制在ΓS平面上,可用于找到给定噪声系数的适当源终端。为了同时考虑噪声和增益,我们还需要在ΓS平面上绘制等增益圆。对于单边设备来说,这是直接的,因为输入和输出匹配部分的增益是相互独立的。
根据先前示例中使用的晶体管,让我们设计一个具有最大可能增益的放大器,其噪声系数为2.5 dB。晶体管的S12很小,这表明它可能被视为单边的。应用单边特性的优良指标(U),我们可以得到:
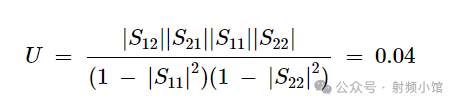
(8)
由于U小于0.1,我们立即知道单边方法的误差小于±1 dB。因此,可以应用单边方法。我们还可以计算单边近似的误差界限的确切值。这个计算结果是:
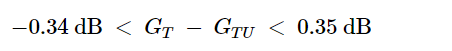
(9)
这意味着我们应该期望在最终设计中实际增益的误差小于约±0.35 dB。
接下来,我们确定GS,max,即单边器件输入匹配部分的最大可能增益:
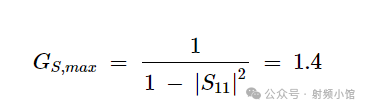
(10)
这相当于1.46 dB。
这使我们能够选择适当的增益圆的数值。在这个例子中,我随意选择了绘制GS = 0.5、1、1.28 和 1.4 dB圆。这些常数增益圆的中心和半径如下表所示。
| Gain | Normalized Gain | Center | Radius |
| GS = 0.50 dB | gS = 0.80 | cS1 = 0.45 ∠ –176.6 ° | rS1 = 0.34 |
| GS = 1.00 dB | gS = 0.90 | cS2 = 0.49 ∠ –176.6 ° | rS2 = 0.23 |
| GS = 1.28 dB | gS = 0.96 | cS3 = 0.52 ∠ –176.6 ° | rS3 = 0.15 |
| GS = 1.40 dB | gS = 0.99 | cS4 = 0.53 ∠ –176.6 ° | rS4 = 0.07 |
图3绘制了这些圆和NF = 2.5 dB圆在ΓS平面上的示意图。
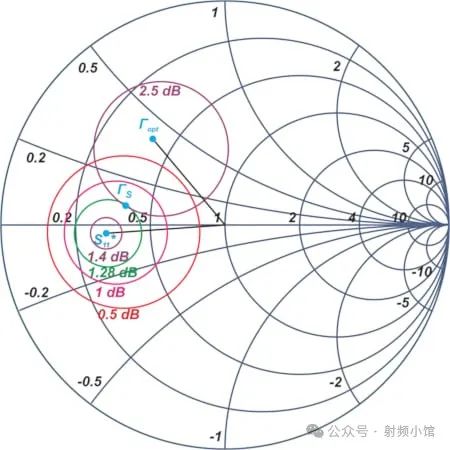
图3
GS = 1.28 dB的增益圆只在ΓS = 0.45 ∠ 169.17 度处与NF = 2.5 dB圆相交。任何更高的GS值都会将我们远离Γopt,导致更大的噪声系数。
对于输出部分,我们选择共轭匹配以最大化增益。这导致:
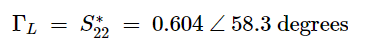
(11)
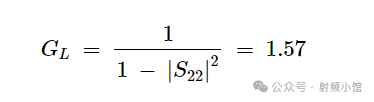
(12)
这相当于1.96 dB。
总增益计算如下:
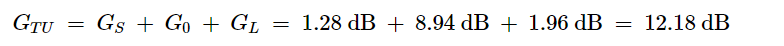 (13)
(13)
在上述公式中,G0 = |S21|2。这是晶体管的基本基于Z0的转换器功率增益。
接下来,我们使用阻抗 Smith图来设计输入和输出匹配网络。对于输入匹配部分,我们在图4的Smith图中定位ΓS,并通过沿着恒定|ΓS|圆的180度旋转找到其关联的归一化导纳(yS)
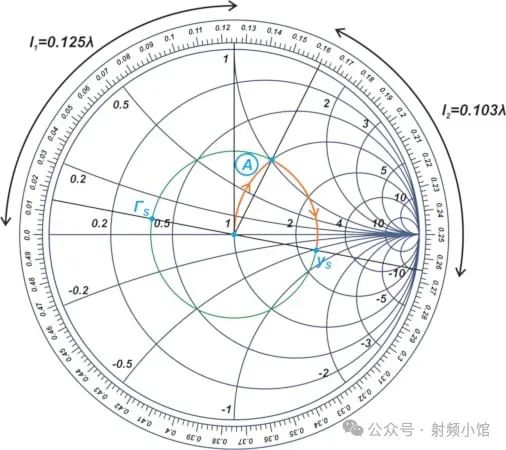
图4
从现在开始,我们用导纳 Smith图。我们希望设计一个电路,将我们从位于50Ω终端的图表中心带到yS。恒定|ΓS|圆与1 + jb圆的交点被标记为点A,其感抗大约为j1。
在设计两端口网络的输入匹配部分时,我们在50Ω终端上添加了一个长度为l1 = 0.125λ的并联开路支路,以得到一个感抗为j1。然后,我们添加一个长度为l2 = 0.103λ的串联线,沿着恒定|ΓS|圆移动到yS。
输出匹配部分可以用类似的方式设计。如图5所示,输出匹配网络需要一个长度为l3 = 0.157λ的开路支路和一个长度为l4 = 0.243λ的串联线。
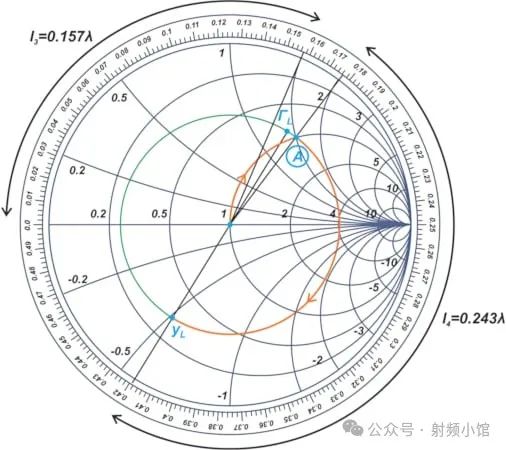
图5
最终的LNA的设计原理图如图6所示
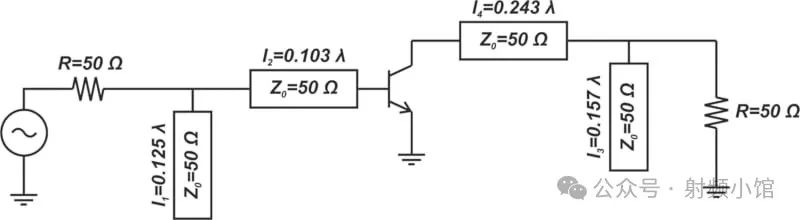
图6
向 Touchstone 文件添加噪声参数
正如我们在最近关于射频放大器稳定技术的文章中学到的那样,Touchstone(.s2p)文件格式通常用于射频设计软件中指定两端口网络的S参数。下图显示了图6中放大器的S参数的.s2p文件。尽管这是可选的,但噪声参数也包含在文件的末尾。

回想一下,以#符号开头的选项行包含头部信息。这个头部信息指定了频率单位和S参数的数据格式。选项行中的“R 50”一词表示S参数的负载终端电阻为50Ω。以!符号开头的行是注释行。
正如你所见,噪声参数没有单独的选项行。为了使模拟器能够区分S参数数据的结束位置和噪声数据的开始位置,噪声参数的第一个频率必须小于或等于S参数的最高频率。
噪声信息的数据格式如下:
第一列指定频率(1400 MHz)。第二列给出最小噪声系数(1.6 dB)。接下来的两列给出最佳反射系数的幅度和相位(Γopt = 0.5 ∠ 130度)。最后一列是有效噪声电阻(RN = 20Ω),将其归一化到我们在选项行中定义的系统阻抗。
将上述.s2p文件链接到Pathwave ADS中的s2p组件,我们可以分析系统的增益和噪声性能。我们生成的Pathwave ADS原理图如图7所示。
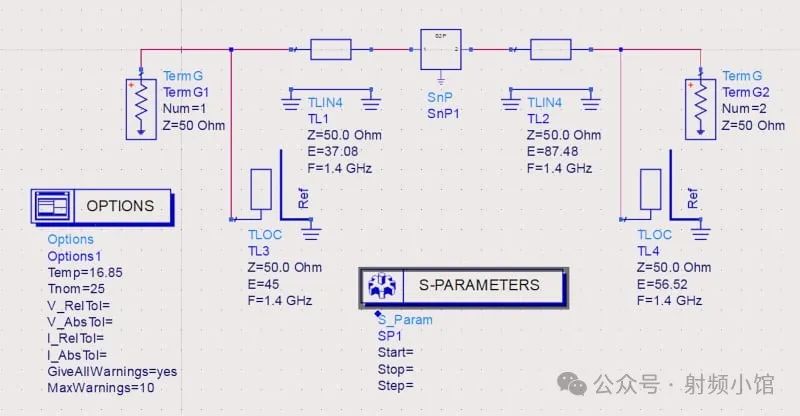
图7
请注意,仿真温度设置为16.85°C,确保噪声系数测量与IEEE噪声系数定义保持一致。计算分析显示,我们设计的电路增益为12.466 dB,噪声系数为2.522 dB。这些数字与我们的设计规格非常接近,可以接受。
来源: 本文转载自射频小馆 公众号
审核编辑:汤梓红
-
 pc16211
2024-04-26
0 回复 举报PC6100_5V精密CMOS带宽放大器,具有轨对轨输入输出功能,替代AD8655 收起回复
pc16211
2024-04-26
0 回复 举报PC6100_5V精密CMOS带宽放大器,具有轨对轨输入输出功能,替代AD8655 收起回复
-
低噪声放大器设计资料2022-11-22 1287
-
宽带低噪声放大器噪声分析2010-05-13 3164
-
低噪声放大器,低噪声放大器型号参数2017-09-11 6137
-
CDMA低噪声放大器设计方案2019-07-09 1888
-
怎样设计和仿真低噪声放大器?有什么流程?2021-04-07 2448
-
关于CMOS多频段低噪声放大器设计方案你想知道的都在这2021-04-14 1089
-
求一种2.4 G的低噪声放大器的设计方案2021-04-21 1670
-
求一种高线性低噪声放大器的设计方案2021-04-22 2046
-
低噪声放大器介绍2021-07-27 3540
-
低噪声放大器设计的理论基础2009-10-20 6404
-
低噪声放大器,低噪声放大器是什么意思2010-03-05 4023
-
Skyworks低噪声放大器从复杂变简单设计方案2010-03-17 1436
-
低噪声放大器简介2023-01-07 2747
-
低噪声放大器的设计原则2023-07-25 2755
-
低噪声放大器工作原理详解2023-09-05 6179
全部0条评论

快来发表一下你的评论吧 !

