

NVIDIA首席科学家Bill Dally:深度学习硬件趋势
电子说
描述
算法(“燃料”):大多数深度学习算法在基本形式上自20世纪80年代以来就已存在,如深度神经网络、卷积网络和使用随机梯度下降和反向传播进行训练的方法。
数据(“空气”):大型标记数据集一直存在,特别是对于无监督学习所需的数据。对于监督学习,像Pascal和ImageNet这样的大型标记数据集自2000年代初就已存在。
计算(“火花”):点燃算法和数据需要足够的计算能力,即在合理的时间内,使用足够多的数据来训练一个足够大的模型。
当前人工智能的复兴,包括生成式AI如ChatGPT在内,可归因于深度学习的进步。基于深度学习的系统如今在语音识别、物体分类以及诸如象棋等游戏中的表现已经超越了人类能力。
深度学习的成功得益于强大且高效的计算硬件。尽管深度学习的算法自上世纪80年代就存在,但直到最近十年,随着强大GPU的问世,这项技术才变得实用。深度学习的进展现在受到硬件性能的限制。在过去的十年中,GPU上深度学习推理的效率提高了1000倍。其中很大一部分增益归功于数据表示的改进,从Kepler一代GPU的FP32开始,并在Hopper一代中扩展到Int8和FP8。
本次演讲将回顾这一历史,并讨论数字表示的进一步改进,包括对数表示、最佳剪裁和每向量量化。
简介:
Bill Dally于2009年1月加入NVIDIA担任首席科学家,此前在斯坦福大学任职12年,担任计算机科学系主任。Dally及其斯坦福团队开发了系统架构、网络架构、信号传输、路由和同步技术,在今天的大多数大型并行计算机中都可以找到。Dally此前曾在麻省理工学院从事研究,从1986年到1997年,在那里他和他的团队建造了J-Machine和M-Machine,这是实验性的并行计算机系统,开创了机制与编程模型的分离,并展示了非常低的开销同步和通信机制。
从1983年到1986年,他在加州理工学院(CalTech)设计了MOSSIM模拟引擎和Torus路由芯片,开创了“虫洞”路由和虚拟通道流控制。他是美国国家工程院的院士,美国艺术与科学学院的院士,IEEE和ACM的会士,并获得了ACM Eckert-Mauchly奖,IEEE Seymour Cray奖和ACM Maurice Wilkes奖。他发表了250多篇论文,拥有120多项授予的专利,并是四本教科书的作者。Dally获得了弗吉尼亚理工大学电气工程学士学位,斯坦福大学电气工程硕士学位和加州理工学院计算机科学博士学位。他曾是Velio Communications和Stream Processors的联合创始人。
-----

现在,身为一名计算机架构师,致力于深度学习,这确实是一个令人心潮澎湃的时刻。

我将尝试与大家分享一些事情。就像现在的大多数人一样,当我准备这场演讲时,我首先让ChatGPT为我草拟了一份讲稿。因此,这就是演讲的初稿。
那么,如何构建一个关于深度学习硬件的演讲呢?这让我相当困惑。于是我说,好吧,这不行。一切都得依靠工程指导。我不得不思考,Bill Dally可能会对深度学习硬件有何见解。这或许是一个合理的演讲主题,但并非我所要探讨的内容。然而,我觉得这个想法很有趣。
如果你想更深入地了解——我总是喜欢在演讲中穿插一些最新的资料——这是昨天《华尔街日报》上的一篇文章,是我与该报记者进行的一次访谈,内容关于我们如何继续推动深度学习的发展。这确实是本次演讲的核心议题。但我会比记者更深入地探讨一些技术细节。
顺便一提,这是我们的Grace Hopper超级芯片的照片。左边是H100 GPU,右边是Hopper多核CPU。实际上,它们的结合非常出色,尽管我作为一名并行计算的信徒,这款CPU的主要目的是为GPU提供更多的高带宽内存。它是一个出色的内存控制器。
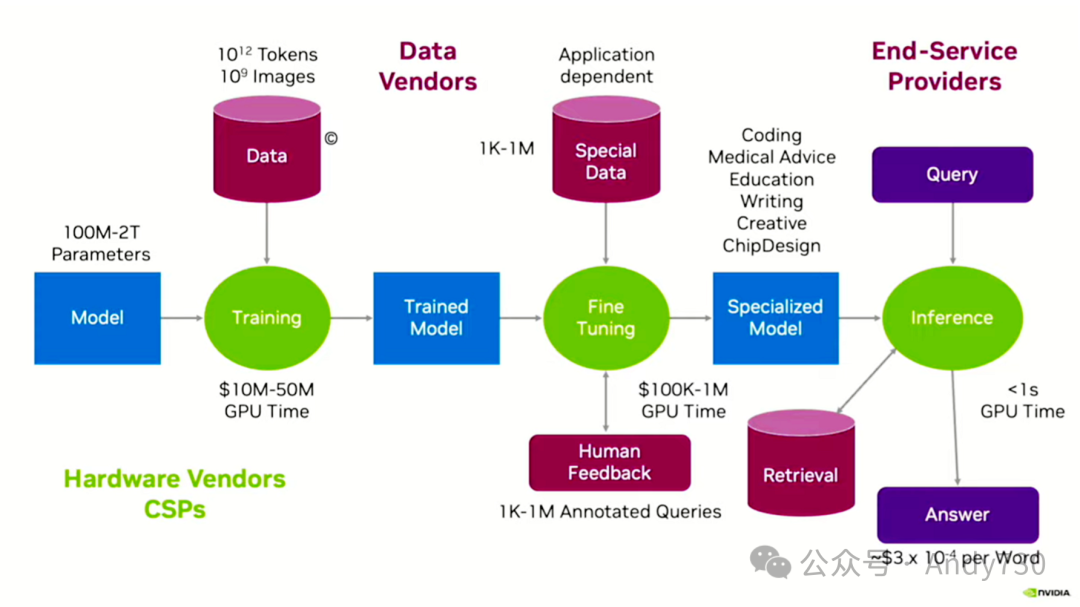
当我们研究像现在每个人都在使用的大型语言模型这样的技术时,我认为,他们真正在做的是将数据提炼成价值,这确实是——计算机科学的主要目标之一。
我们通常从大量数据出发。人们往往会利用他们可以从互联网上搜集到的所有信息来训练这些模型。这些数据集包含高达10的12次方个token——一个token大致相当于一个单词——当通过分词器处理它时,通常会得到1.5到2个token对应一个单词的比例——以及可能达到十亿级别的图像数量。这就是数据集规模。我们希望从中提取价值。这种价值体现在能够回答问题、提升工作效率,比如通过拥有教学助手来帮助老师给予学生更多个性化关注,或者辅助医生做出更准确的诊断。大型语言模型正广泛应用于这些领域。
思考这个问题的方式就像是在考虑如何将学生送入大学。这就是你拥有万亿级别token数据集的意义所在。实际上,我之前做过类似的幻灯片。现在,大型模型的训练已经涉及10万亿甚至更多的token。对于万亿token数据集,需要在AWS上投入相当可观的资金来购买计算时间。
顺便提一下,购买GPU也是一笔不小的开销。在AWS上,这些费用是资本化的,即使只租用三个月并付清了费用,他们也不会将GPU转让给你。然后运行一个训练作业。现在,拥有了一个训练有素的模型。
这是一个在本科教育阶段接受过广泛训练的大型语言模型,相当于对互联网上的所有标记都有了一个基础的文科教育背景。但在实际应用中,你可能希望模型更加专业化,比如专门用于医学或教学领域。这时,就需要将模型送入研究生院进行深造。在研究生院,你可以进行一系列的组合操作,其中之一就是所谓的预训练(pretuning),即在特定数据集上继续训练模型。
在NVIDIA内部,我们使用的模型名为ChipNeMo,它旨在提高我们的硬件设计师的工作效率。NeMo是我们的通用大型语言模型,而ChipNeMo则是在240亿个标记上进行了预训练,这些标记主要来源于自1990年代中期以来我们设计GPU的架构文档、Verilog代码、脚本等。ChipNeMo最显著的应用是帮助高级设计师节省时间,因为高级设计师通常需要花费大量时间回答初级设计师的问题,例如“纹理单元是如何工作的?”等。通过向ChipNeMo提问,高级设计师可以得到准确且有力的答案,因为ChipNeMo已经阅读了所有相关的架构文档。
在预训练之后,你还需要进行微调,使模型更加符合人们的喜好。这通常是通过让模型生成多个查询回复,并让人类对这些回复进行评分来实现的。通过收集人类的反馈,你可以不断优化模型,使其生成的回复更符合人们的口味。在这个过程中,人类的参与至关重要,因为他们的反馈是提升模型质量的关键。
有意思的是,尽管开始时对模型进行文科教育的成本很高,但人们可以通过微调来降低这一成本。据我估算,微调的费用大约在10万到100万美元之间。尽管这个数字可能很高,但人们已经通过利用仅花费几千美元的GPU时间,完成了非常有效的微调工作。因此,一旦拥有了专业模型,就可以开始实际应用了。
从长远来看,深度学习的大部分计算都集中在推理阶段。在深度学习探索的早期阶段,训练工作确实非常繁重,因为人们需要进行大量的实验。然而,一旦他们找到了合适的模型,他们就可以定期重新训练这些模型,并在模型上进行推理。这个过程可能会持续几个月甚至更长时间,然后再重新进行整个训练过程。因此,大量的工作实际上是在推理阶段完成的。即使每个查询可能只需要一秒钟的GPU时间,但当进行足够多的查询时,这实际上会占据训练阶段花费的几个月的时间。
这张幻灯片的最新补充部分,我稍微插入了关于检索增强生成的内容。这是近四五个月来非常流行的一种做法。在运行大型语言模型和进行推理之前,我们会使用查询来查询数据库,提取所有相关文档。对于ChipNeMo模型,我们回到了最初的240亿个标记文档数据库,提取了所有相关的架构文档,然后将它们与原始查询一起输入到模型的输入窗口中,然后运行推理代码。这种做法可以防止大型语言模型使用虚构的信息,因为它主要基于实际文档进行操作。它可以为我们提供真实文档的引用,并大大提高准确性。
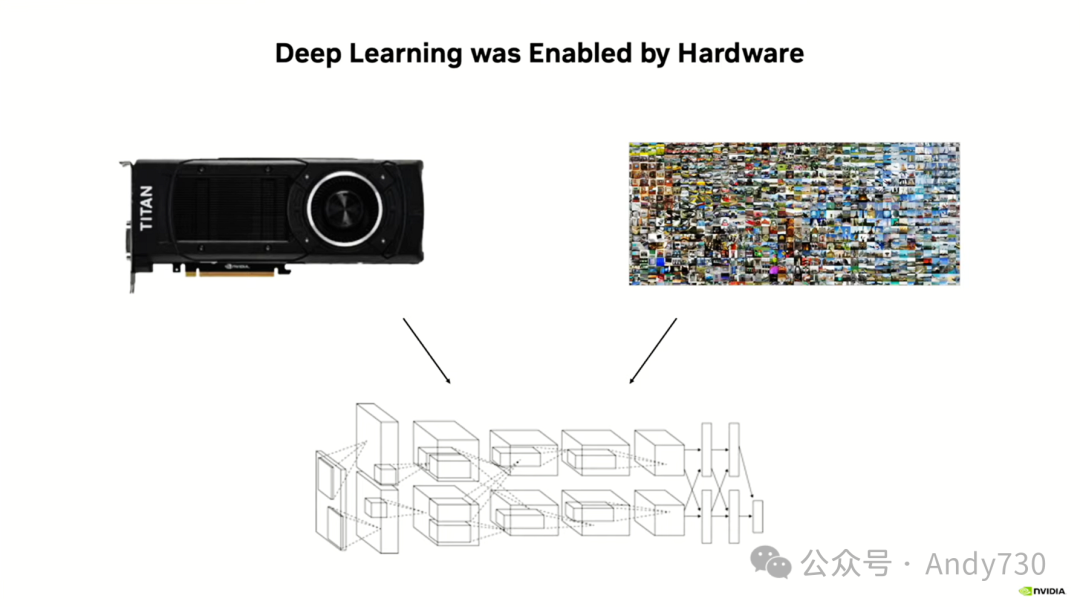
接下来,我将先介绍一些动机,然后我们将讨论我们是如何走到这一步的。而讲座中最令人兴奋的部分将是我们接下来将走向何方。
让我们从一些动机和历史背景开始探讨。当前的深度学习革命是由硬件推动的。我喜欢将深度学习视为由三个要素构成的。它们分别是算法、数据和计算能力,这可以类比为燃料、空气和火花。
首先,算法是这里的“燃料”。大多数这些算法,至少在它们的基本形式上,自20世纪80年代以来就已经存在了。深度神经网络、卷积网络,以及使用随机梯度下降和反向传播进行训练的方法,这些都在80年代就已经出现——在某些情况下,甚至更早。
接下来是“空气”,即数据。大型标记数据集一直存在,特别是对于无监督学习所需的数据。而对于监督学习,像Pascal和ImageNet这样的大型标记数据集自2000年代初就已经存在了,所以在真正的“火花”点燃之前至少有10年的时间。
然而,点燃这种燃料和空气混合物的“火花”是足够的计算能力。这指的是在合理的时间内,使用足够多的数据来训练一个足够大的模型。以最初的ImageNet数据集为例,它大约包含1000万张图像。而足够大的模型则是AlexNet。我稍后会展示这个训练对下一张幻灯片的要求。当时,训练这样一个模型需要花费两周的时间,实际上是在一对采用Fermi架构的GPU上完成的。
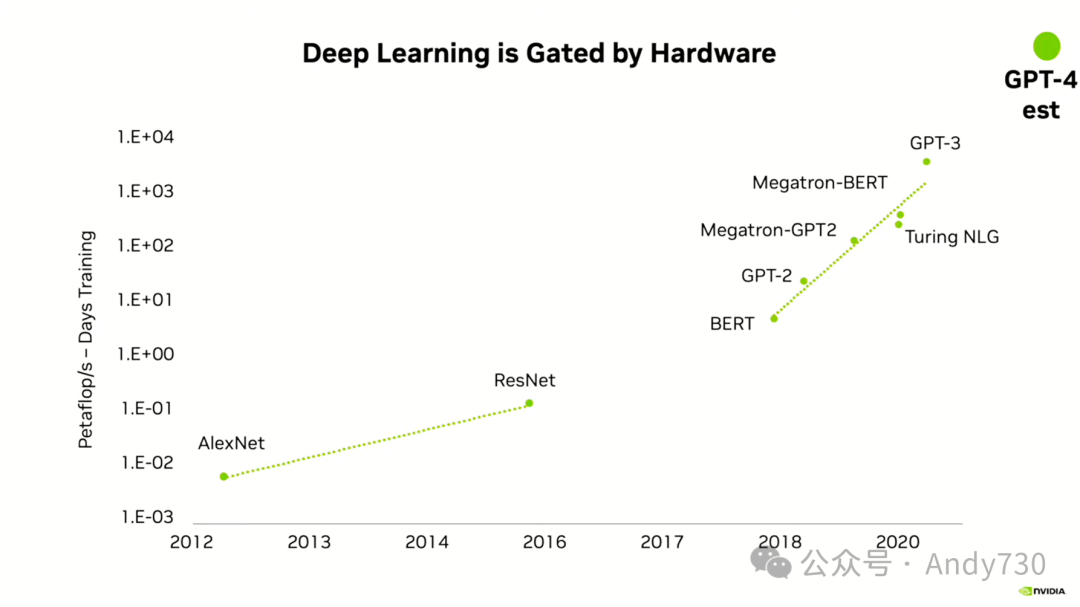
自那时起,深度学习的进展受限于我们能够应用的计算力。考虑到AlexNet的训练时间,它基本上是每秒千亿次浮点运算的百分之一——也就是说,如果我们有一台每秒千亿次的机器,你会花费百分之一的时间在上面。我估算这大约是一个小时的四分之一,即15分钟,在每秒千亿次的机器上。在2012年至2016年的ConvNet时期,我们提高了大约两个数量级的计算力。因此,当我们达到ResNet时,我们大约拥有了每秒千亿次的计算能力。
自2018年开始使用BERT进行大型语言模型的训练以来,我们每年大约提高了一个数量级的计算力。对于GPT-4,虽然OpenAI没有发布该模型的详细信息,但根据网络上的各种传言,我估算在2023年训练GPT-4大约需要100万台每秒千亿次的机器。在大约十年的时间里,最先进的深度学习模型的计算需求增加了10的8次方倍。我们付出了巨大的努力,个体GPU的性能提高了约1000倍,另外的10的6次方倍增加来自于GPU数量的扩展和训练时间的增加。
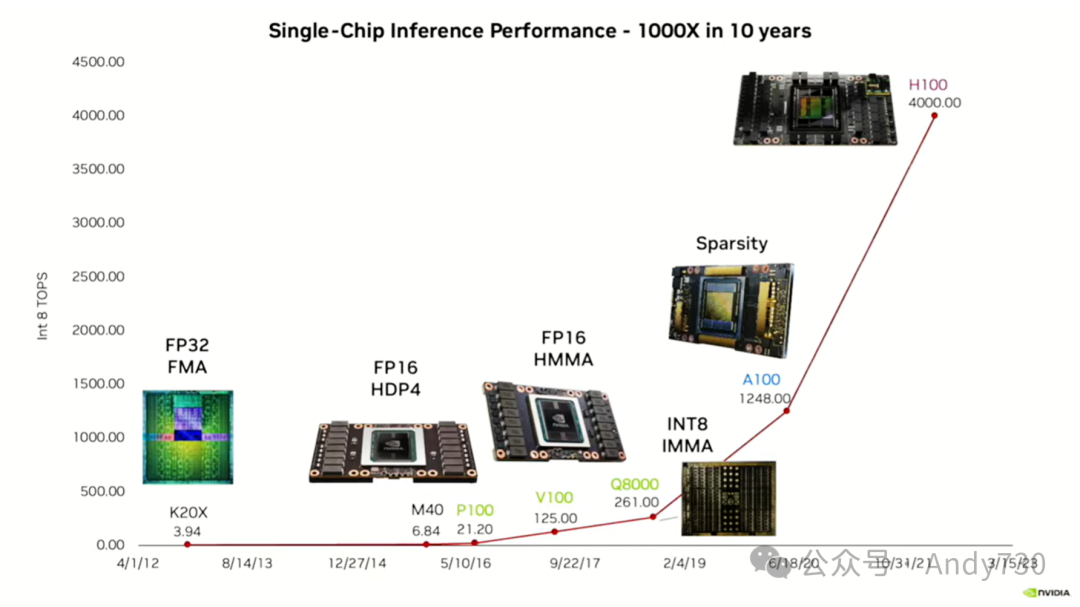
接下来,让我稍微谈谈历史。这是我想称之为“黄氏定律”的曲线,以我们的创始人、NVIDIA的Jensen Huang命名。在深度学习领域,我们的推理性能在过去十年基本上每年翻一番,从大约四开始。这是Kepler世代单芯片推理中的INT8 TOPS,而在Hopper世代中则达到了4000。在10年内,性能增加了1000倍。如果每年翻一番,那么应该是1024倍。那么我们是如何实现这一壮举的呢?实际上,我将在下一张幻灯片中为你揭晓。
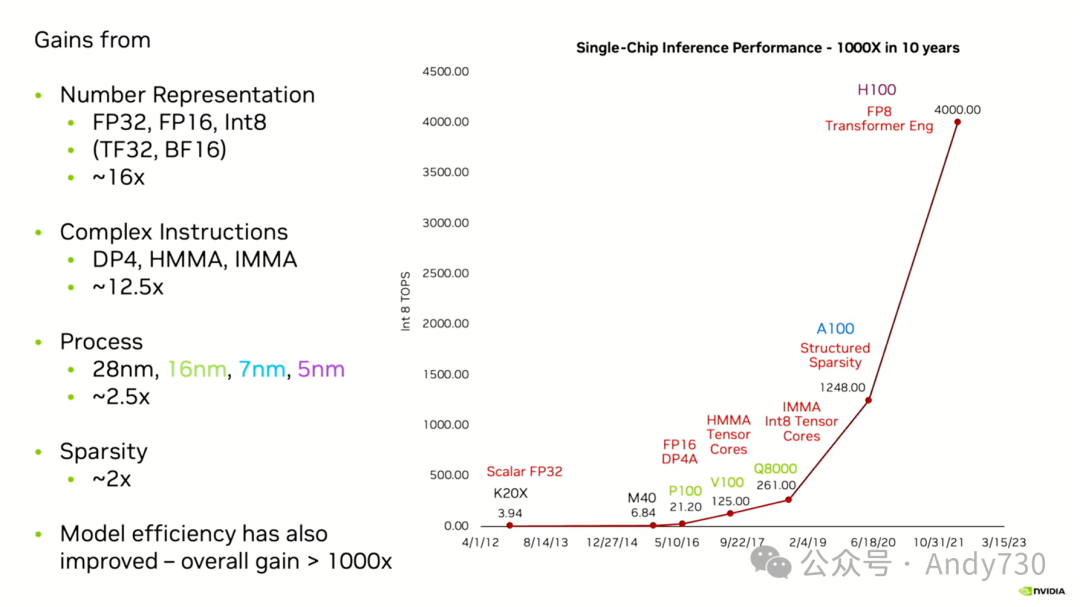
主要的收益按照其贡献程度列在这里。其中最大的收益来自于使用更小的数字。以Kepler为例,它原本并非专为深度学习设计,而是为科学计算打造,支持FP64和FP32图形处理。因此,在推理过程中,人们使用INT8在FP32环境中完成操作,导致数字需要放大四倍。然而,昂贵的算术运算是乘法,其成本与比特数的平方成正比,因此成本实际上增加了16倍,而非4倍。
在2017年的ISCA会议上,Dave Patterson发表了关于Google TPU V1的演讲,声称其比NVIDIA GPU更高效。然而,TPU V1的整体性能优势——更确切地说是能源效率优势——主要归功于其执行INT8操作的能力。Patterson将TPU V1与Kepler进行比较,尽管当时他本可以将其与更先进的Volta甚至Turing进行比较。Kepler是五年前的产品,主要支持FP32。因此,这一切都与这16倍的成本增加有关。
接下来的主要收益来自于执行复杂指令。我将为此展示一张幻灯片,并详细介绍相关内容。即使在GPU的简化管道中,不进行分支预测和乱序执行,执行一条指令的成本仍然比该指令中的算术运算的成本高出约20倍。在更低的精度下,情况更糟,尤其是针对FP16。为了分摊这一成本,需要用一条指令完成更多的工作。因此,添加复杂指令成为了一个重要的优化方向。我们从Kepler世代的最大指令FMA转变为Pascal世代的四元素点积DP4,再到我们的矩阵乘法指令,如HMMA用于半精度矩阵乘积累加和IMMA用于8位整数矩阵乘积累加。这些指令的引入分摊了一些开销,为我们带来了额外的12.5倍性能提升。
这里展示了四代工艺技术,它们以颜色进行区分——黑色、绿色、蓝色等。Kepler和Maxwell采用了28纳米工艺,而Pascal、Volta和Turing则采用了16纳米工艺。Ampere是7纳米工艺,而Hopper更是达到了5纳米工艺。然而,从28纳米到5纳米的巨大跃迁只为我们带来了大约2.5倍的性能提升。我内部有一个电子表格,一直在跟踪这些数据。因此,我们并没有从传统的工艺技术提升中获得太多好处,主要的提升来自于更先进的架构。另一个重要的架构贡献是稀疏性。当我展望未来时,我相信稀疏性将为我们带来更多的性能收益。目前,我们仅在权重上利用了2比1的稀疏性,但我们可以实现更高级别的稀疏性,并将其应用于激活上。
此外,我还想提到,算法领域的进步也非常显著。我认为,仅通过多年来模型效率的提升,我们就已经实现了另外1000倍的性能增长。以ConvNet时代为例,当大家都在ImageNet竞赛上竞争时,从VGGNet到GoogleNet的转变就是一个很好的例子。GoogleNet是一个更高效的网络,它去掉了完全连接的后端,采用了可分离卷积和旁路等技术,使网络效率提高了数个数量级。因此,他们能够在不增加太多操作的情况下,实现性能上的巨大提升。这样的模型还有很多。
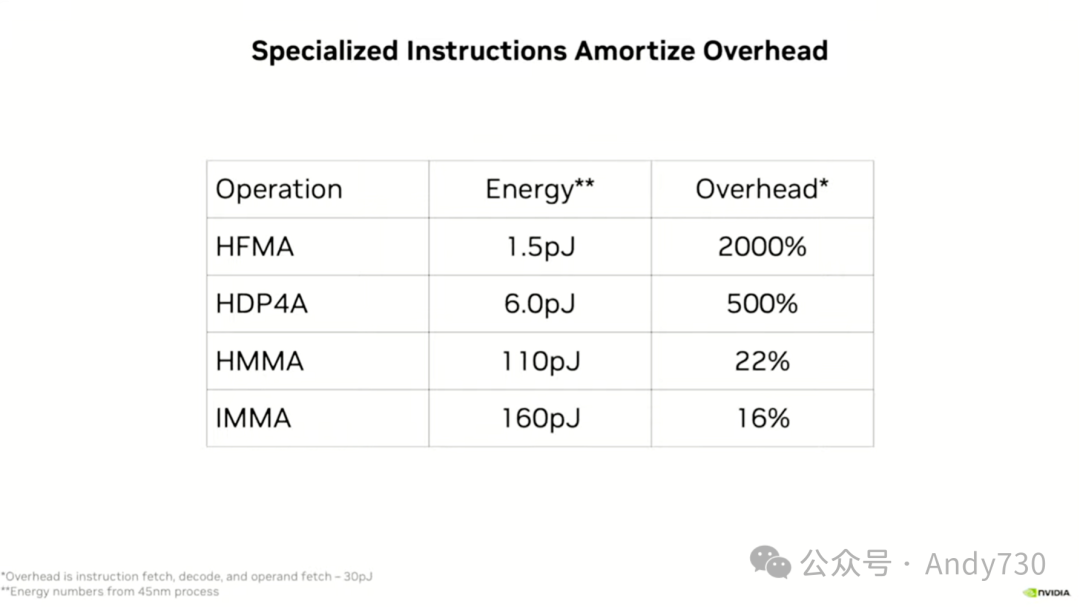
让我们来谈谈复杂指令及其重要性。正如我之前提到的,即使对于具有非常简化管道的GPU,执行指令的开销因子也约为20。而对于执行复杂、乱序CPU操作的CPU,比如执行FP16操作,这个开销因子更接近1000。这也是为什么我们不希望在CPU上进行深度学习的原因之一,除非我们全部使用MMX指令进行。
如果我们的工作仅限于融合乘加运算,那么我们实际上在执行两个算术运算。这意味着,我们的大部分能量都消耗在了开销上,就像一个大公司运营的成本。但如果我们能够至少执行八个操作——比如,一个点积运算就需要四次乘法和四次加法,总共八个操作——那么有效负载的能量就会增加到六。尽管开销能量保持不变,但开销相对于有效负载的比例会下降到五倍。尽管如此,我们仍然在开销上花费的能量比在实际操作上花费的要多。
在Volta世代,我们引入了一个被市场人员称为张量核心的功能,它实际上是一个专门用于执行矩阵乘法的指令。HMMA,即半精度矩阵乘积累加,能够接收两个FP16的4x4矩阵,并执行矩阵乘法。这意味着你需要将每个元素与另一个矩阵的每个元素相乘,这是一个n的三次方操作,即4x4x4,总共64次乘法。然后,你需要将这些结果全部加起来,并存储到一个FP32的4x4矩阵中。这样,总共进行了128次操作。尽管操作的总能量是110,但现在的开销比例已经降低到了22%。
到了Turing世代,我们又引入了整数版本的该操作,即IMMA。它接收两个8x8的INT8矩阵,进行乘法运算并求和。而在Hopper世代,我们更进一步,引入了四分之一精度矩阵乘加法,使用FP8进行运算。需要强调的是,一旦我们拥有了这些大型指令,我们的完全可编程GPU在深度学习方面的效率就可以与硬连线的加速器,如TPU或其它专用芯片相媲美。因为这些专用芯片也并非毫无开销。它们同样需要移动数字,而不仅仅是进行矩阵乘法运算。它们的开销可能也在15%到20%左右。因此,在这个时间点上,我们的效率与专用加速器相当,同时我们还拥有可编程引擎的所有优势,背后是一个成熟的编程系统和几十年来积累的库支持。
听众:这是能源开销方面的讨论,对吧?还有其它的吗?
Bill Dally:没错,能源确实是一个很好的衡量标准。

那么,我们目前进展到了什么阶段呢?如今,我们有了Hopper。它具备一千万亿次的TensorFloat-32运算能力。根据数据的稠密程度或稀疏程度,它的FP16或BF16运算能力为1到2千万亿次,而FP8或INT8的运算能力为2到4千万亿次。它的内存带宽超过3TB/s,高达94TB,这里的94是准确的,配备了96GB的HBM3内存。此外,它还拥有18个NVLink端口,为我们提供了900GB/s的带宽,而整个芯片的功耗为700瓦。不过,有一点需要指出的是,将这个部件运往中国是违法的,这种做法其实并不明智,因为对这种部件的出口限制只会促使中国的程序员为华为部件编写代码,这对美国并无益处。
这个部件拥有一些令人印象深刻的功能。事实上,我亲自为这个部件中的动态规划指令撰写了建议书,以加速生物信息学代码的运行。因此,如果你需要进行动态规划来进行基因序列匹配,这个部件将会表现出极高的运算速度。
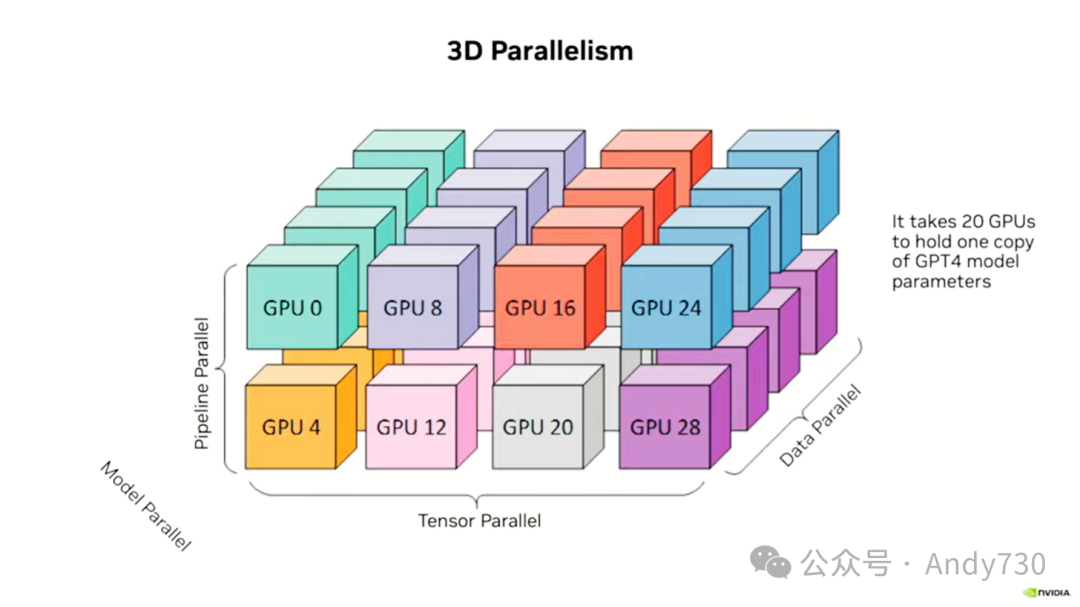
关于比值——当我分享我们在加速器上所做的一些实验时,我会详细解释这一点——它达到了每瓦9兆次的运算性能。这是基于INT8或FP8数学运算的结果。这也是我们评估不同深度学习解决方案效率的一种方式。尽管我们已经实现了1000倍的性能提升,但我们还需要达到10的8次方倍的目标。那么,剩下的性能提升从哪里来呢?答案在于使用多个GPU。事实上,你必须使用多个GPU,因为单一的GPU无法容纳像GPT-4这样规模高达1.2万亿参数的模型。在进行训练时,每个参数大约需要20字节的存储空间,这不仅包括了参数本身,还包括了动量系数、训练算法以及其它一些开销。因此,要保存一个GPT-4的完整副本,我们需要大约20个GPU。
因此,我们将工作划分为两个维度的并行化。
首先是张量并行,这涉及多个GPU协同工作在一个模型副本上。具体来说,我们将单个矩阵进行切片处理,通常只在一个维度上进行切片,例如将矩阵切分成列条。然后,我们进行相应操作,并将结果汇总。
另一个维度是管道并行,我们将网络的不同层分别部署在不同的GPU上,并将结果逐层传递。值得注意的是,早期的层并不会闲置,而是在处理后续数据批次的同时,开始处理下一批训练数据。随着规模的进一步扩大,我们还会采用数据并行策略。这意味着我们将运行模型的不同副本,并将一个训练数据批次分割到这些副本中,使它们各自进行训练。之后,它们会交换权重更新,以确保在下一次迭代中每个副本都拥有相同的权重集。

为了实现这些并行化策略,我们设计了一系列硬件。首先是DGX服务器,它配备了8个H100 GPU和四个我们的NV交换机。这些交换机负责连接从H100 GPU引出的NVLink互连。尽管我不能详细介绍每个细节,但这款服务器具备32 petaFLOPS的计算能力,功耗为11千瓦,背板输出达到900GB/s。

除了上述的四个NV交换机外,为了连接更多这样的服务器,我们还设计了一个类似披萨盒的装置。这个盒子里装有两个NV交换机,通过它和使用主动光缆,可以构建更大规模的系统。

因此,通常向客户提供的解决方案看起来像这样:一个DGX超级机架。在这个机架中,每个小金色前面板板子上都装有一个HGX100,它集成了8个GPU。可以使用NVLink将多个这样的机架连接起来,或者在某些情况下,采用InfiniBand网络——中间那些是InfiniBand量子交换机——并将所有这些设备整合在一起。
这样做的好处有很多。首先,软件是预配置的。因此,当从NVIDIA购买这样的机器,并在你的数据中心中将其连接好,插入所有主动光缆后,只需简单地开机,便可以在一小时内开始训练深度学习模型。相反,如果尝试从头开始配置所有网络设置并进行调整,那可能需要耗费一个月的时间。我过去曾与Cray和其它公司合作构建了许多超级计算机。但通常情况下,从我们在洛斯阿拉莫斯或橡树岭等地将这些机器完全组装并放置在地板上,到它们能够运行一个有用的问题,往往需要六个月的时间。这是因为启动和调整过程需要花费大量时间。而通过使用预配置的系统,我们已经解决了这些问题。可以简单地开机,它就能立即投入工作。这并不是因为硬件存在故障,而是需要花费大量时间来准备和调整软件。
观众:那么这台机器是否更侧重于训练任务呢?
Bill Dally:其实它同样适用于推理任务。此外,还可以根据自己的需求配置所需的带宽。机器内部的带宽是预配置的,有八个GPU通过NV交换机连接在一起。但在背板上,可以选择是否将所有GPU都连接起来。同时,我们还提供了PCIe插槽,用于安装InfiniBand网卡。因此,可以根据实际需要决定连接多少网卡。这样,可以为每个盒子提供所需的带宽。
对于训练任务来说,另一个突出的优点是,无论是NVLink网络还是InfiniBand网络都支持网络集合功能。这意味着在进行数据并行训练时,每个GPU都需要交换权重。通过网络集合功能,你只需发送你的权重并接收总和,而无需进行逐个交换和相加的操作。这极大地提高了数据并行训练的有效网络带宽。
接下来,让我们来谈谈软件方面的一些内容。
有时我想说,关于深度学习的一点是,虽然任何人都可以构建一个矩阵乘法器,但真正让它变得有用的是软件。在NVIDIA,我们从2010年开始致力于深度学习软件的研发。当时,在早餐时我遇到了我的斯坦福同事Andrew Ng,他正在跟我分享关于在互联网上找猫的事情。我一听就觉得,天哪,GPU在这方面比CPU更擅长。于是我指派了一位NV研究部的同事——实际上是一个名叫Bryan Catanzaro的编程语言研究员——与Andrew一起工作,去寻找互联网上的猫。他编写的软件后来演变成了cuDNN。当然,后来Andrew挖走了Bryan,让他在百度工作了一段时间。不过Bryan最终又回到了NVIDIA。从那时起,我们就一直在构建大量的软件。
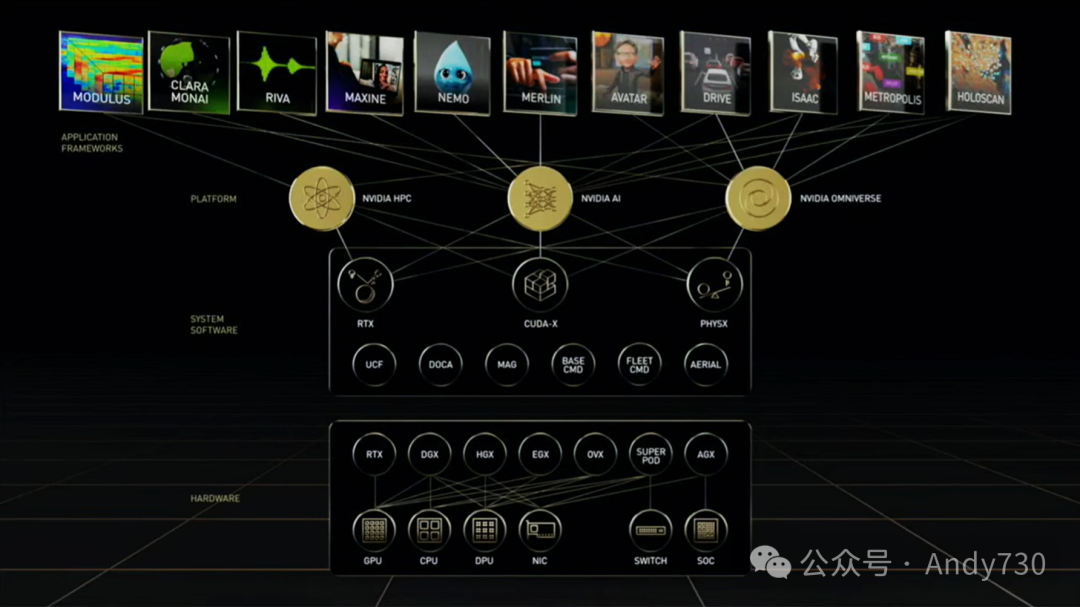
这是我们的软件堆栈的不同层次。我们拥有三个主要的软件堆栈——AI堆栈、HPC堆栈,以及我们称之为Omniverse的图形堆栈。在此基础上,我们还建立了许多垂直领域,涵盖了从Clara的医疗诊断到Modulus的物理模拟,再到Drive的自动驾驶汽车技术等各种领域。这里涉及到的软件工作量可能高达成千上万人年。这种努力在MLPerf基准测试中得到了真正的体现。
我认为MLPerf是一个非常好的衡量标准——我喜欢查看它以了解竞争对手的情况,也了解整个深度学习社区的发展状况。这真的很棒。
我的意思是,在CPU领域,当我在80年代和90年代从事CPU架构工作时,有SPECmark基准测试,大家都会在这个基准上进行竞争。但随着时间的推移,它们变得有些不自然了。我认为MLPerf基准测试真正出色的地方在于,它们定期推出新的基准测试。现在他们有一个LLM基准测试,还有一个很好的推荐基准测试。他们紧跟行业发展的步伐,几乎没有延迟。
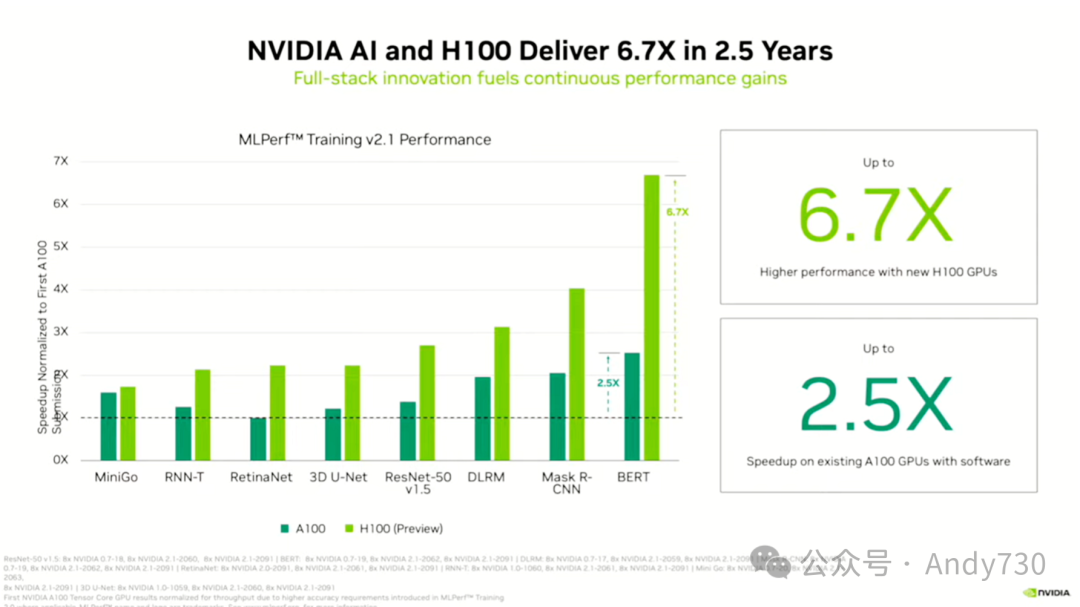
我想通过这张幻灯片传达的观点并不是Hopper比H100刚推出时快6.7倍。事实上,当H100首次推出时,与首次推出的Ampere相比,它的性能提高了2.5倍。这是硬件的进步,更是Ampere软件的改进以及庞大的软件基础所带来的优势。人们可以构建出非常出色的矩阵乘法器,但除非他们在深度学习软件上投入了成千上万人年的努力,否则很难在竞争中脱颖而出。这一点在MLPerf的结果中得到了体现。
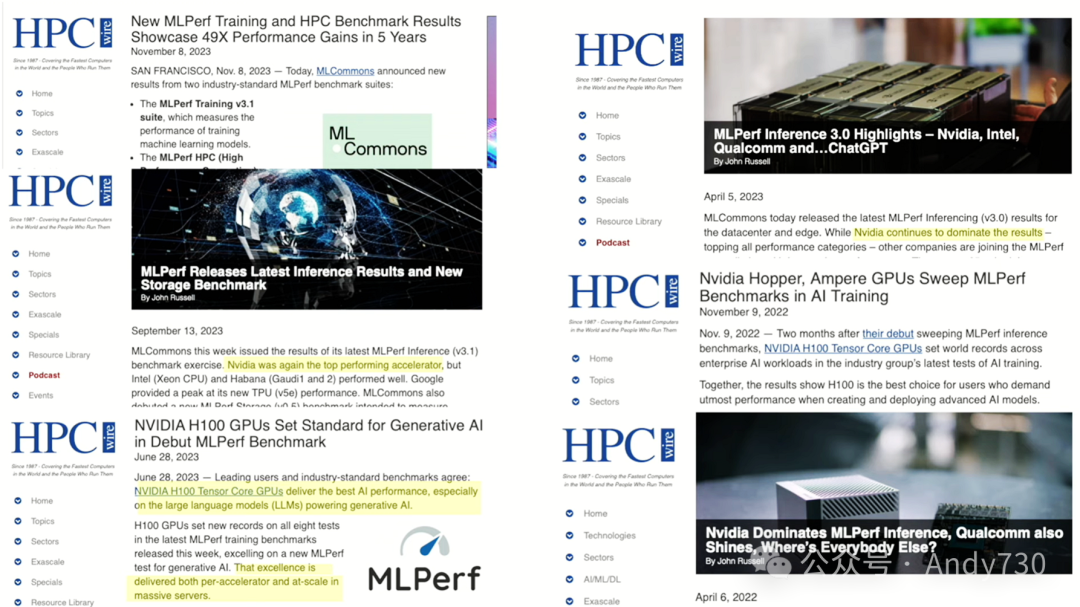
这里只是我剪辑的一些文章标题。最近的一篇是昨天——11月8日。虽然你可能需要仔细阅读文章,才能找到称赞NVIDIA的部分,但在其它文章中,我都强调了NVIDIA在这些方面的优势。
现在的情况就像是电影中的场景,主角们在跑步,后面紧跟着蒙古军队和一大群野兽。他们必须拼命地跑才能保持领先。这就像是现在的NVIDIA,因为每个人和他们的狗都在尝试构建AI硬件,因为他们认为这是下一个淘金热的机会。我们试图保卫我们的领先地位,不是通过阻碍他们的方式,而是试图比他们跑得更快。然而,尴尬的是,他们中的大多数人都会绊倒摔倒,但只需要一个人继续奔跑。如果我们绊倒了,结果就不会好。
那么我们该如何保持领先,就像在古代战争中超越蒙古军队一样,确保我们在AI硬件领域的领先地位呢?
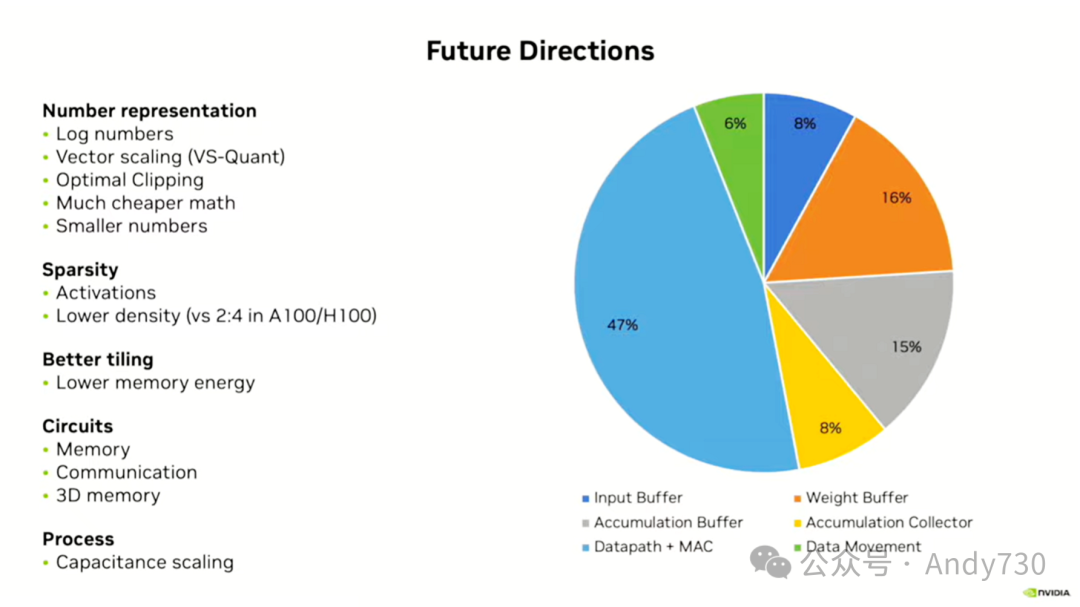
一个很好的方法是绘制一张图表,展示推理过程中能量的流向。在这张图表中,我们可以看到数学、数据路径和数学占据了47%的比例,这意味着我们有一半的能量用于进行数学计算。为了改进这一点,我们需要进行更高效的数学计算,这可以通过采用更好的数字表示或利用稀疏性来减少计算量来实现。
接下来,我们看到图表中的另一个大块是内存,包括累积缓冲区、输入缓冲区、权重缓冲区和累积收集器,还有6%的能量用于数据传输。这主要涉及到将数据从片外存储器传输到片上存储器,以及从大的片上存储器传输到较小的片上存储器。
那么,我们应该如何改进呢?在数字表示方面,我们可以采取多种策略。这里,我将讨论其中几种。我们学到的一个重要经验是,我们应该使用我们能够应对的最经济的数字表示。为了实现这一点,我们需要将数字精确地缩放到该数字表示的动态范围内。接下来,我会分享一些我们发现的有效方法。
此外,我对长数字特别感兴趣,并会介绍一些使长数字加法变得更容易的技巧,因为通常来说,乘法相对容易,因为它们可以转化为加法,但加法却更复杂,因为它们需要转换回整数。
目前,我们主要在权重上使用稀疏性。然而,我们还可以考虑在激活上使用稀疏性,并利用其它低密度特性来利用稀疏性。为了减少那6%的数据移动,我们可以优化平铺策略——基本上是一种更好的循环调度方式,以最大限度地减少移动并提高重用率。
在电路方面,我们也做了很多工作。考虑到内存消耗了大约一半的能量,我们可以通过一些简单的方法来提高内存效率。例如,我们发现这些内存通常是“一次写入,多次读取”的。因此,在写入时使它们在能源上相对昂贵是可以接受的。一种利用这一点的方法是使用每个单元格具有一个位线的设计。这样,你可以写入单元格,然后激活该位线,内存的输出就会输出。这种方法使得写入操作变得非常节能。这只是我们正在考虑的一项改进。我们还有许多其它的改进方案,我会在接下来的部分继续介绍。
针对我们接下来的计划,我们将持续聚焦于优化数学计算和内存使用,以确保我们的硬件在处理深度学习任务时达到更高的效率。此外,我们还将不断探索新的数字表示技术和稀疏性利用方法,以进一步降低能量消耗并提升性能。总而言之,我们的目标是维持在AI硬件领域的领先地位,持续创新和改进,以满足不断增长的深度学习需求。
没错吧?那么,当你在进行读取操作时,你所做的就是从位于乘法器前面的一大堆位线中选择一个,这个读取过程几乎不消耗能量。相反,写入操作是能量消耗的主要环节。因此,你就不需要在每次读取时都切换位线。你只需要进行一次写入操作。情况会有所不同。但在读取时,你只需要切换乘法器的输入即可。
优化通信电路可以带来诸多好处。如果让我指导一个电路专业的学生来设计一种从芯片一端到另一端传递位的信号方式,并鼓励他们尽可能多地消耗能量,他们很可能会采用我们现今的常规做法——利用逻辑电平,其中电源代表1,地线代表0。但实际上,只需稍微增加一些晶体管面积,你就不再需要1伏特的电压来表示1或0了。那么高的电压简直是浪费,且可能对设备造成损害。实际上,你只需要确保足够的能量使Eb/N0达到大约20分贝,就足以保证数据传输的准确性了——可能仅需50毫伏的电压就足够了。因此,通过改进通信电路,我们可以实现很多优化。
我想分享一件令我非常兴奋的事情,我们正在为此付出巨大的努力,那就是通过直接在GPU上方堆叠DRAM来扩大我们的内存带宽,并同时降低内存的能量消耗。但我们必须承认,这个过程中存在许多技术难题需要我们去解决,可能需要几代人的努力才能最终实现。

让我们从数字表示开始讨论。
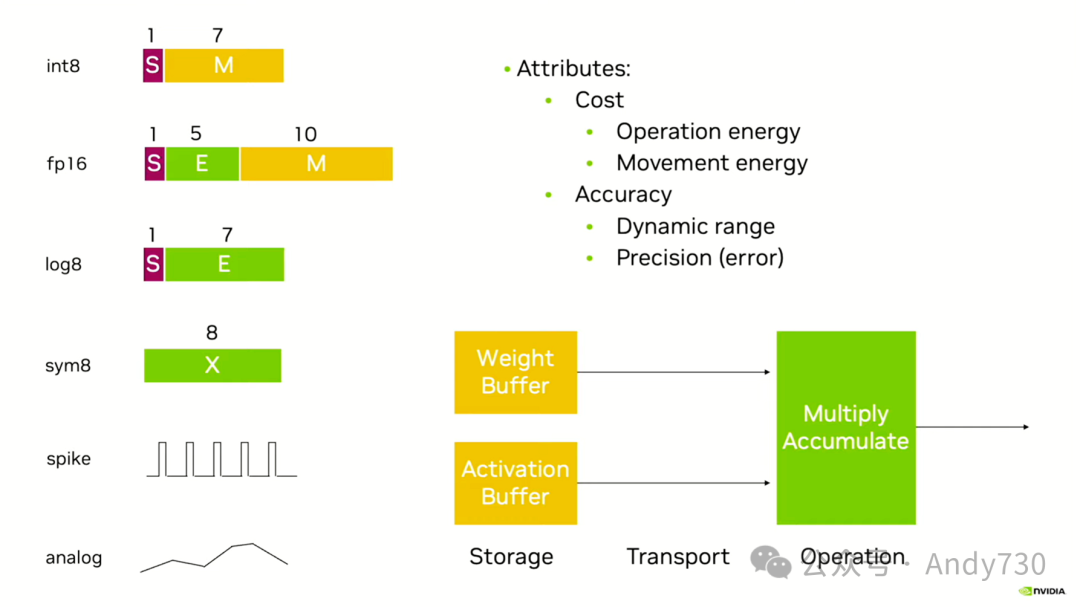
当你问一个数字系统有多好时,实际上你关心的有两个方面。首先是准确性,即实际数字与理论数字之间的差距。在数字系统中,数字必须覆盖整个数字线,因此准确性主要关注的是在将任意数字转换为数字系统时可能产生的最大误差,因为我们通常需要对数字进行四舍五入以匹配可表示的值。另一方面是动态范围,即数字系统可以表示的数字范围有多大。这既涉及到准确性,也涉及到成本。数字位数是一个关键因素。在存储和传输数据时,存储器和线路并不关心这些位的具体值,而是关心你引用了多少位。因此,理论上使用的位数越少越好。但同时,我们还要考虑执行操作的成本,比如进行乘积累加时所需的资源消耗。
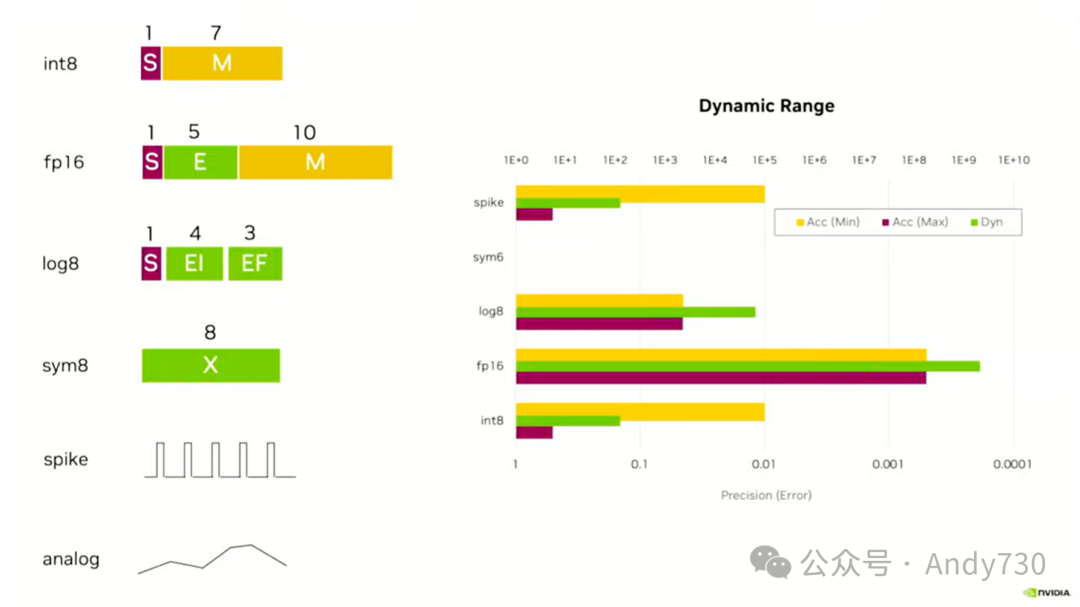
接下来,我会简要介绍一些代表性的数字。使用整数,事实上,其准确性并不理想。原因在于其误差与数值大小无关。不论处理的是小数还是大数,误差都是一个半最低有效位。稍后我会在下一张幻灯片上通过图表来展示这一点。因此,它们在最坏情况下的误差达到了33%。这是1.5和1之间的差异,因为我们必须将1.5四舍五入到2或1。这相当于从1中取走了一半,显然并不理想。相比之下,浮点数的表现要好得多,对数的表现也更好。我应该选择使用对数8和FP8,但我稍后会通过图表来展示这一点。
关于符号,它的表现相当不错。那么,符号具体是什么呢?事实证明,你可以使用反向传播和随机梯度下降来训练各种模型。例如,我和宋曾在ICLR上发表了一篇论文,大约是在2015年,我们训练了一个16条目的码本,以获取代表我们所拥有的权重分布的最佳16个权重。这是一个很好的方法,因为如果你只限于使用16个值,或者64个、256个值,这取决于你使用的位数,这就是你能找到的最佳方式来代表那些权重。这将有助于最小化存储和移动的能量消耗。然而,在实际执行数学运算时,你必须表示你选择的那些点。这意味着你需要在表中进行高精度的查找,而这本身就是一个相当耗时的过程。接下来,我们进行了16位数学运算。最终,我们用这些4位符号进行了16位数学运算,这完全抵消了我们在能量消耗方面的任何优势。这个想法虽然巧妙,但并不实用。
接着,我们来看尖峰表示。我之所以要提到它,是因为如果要从所有能源效率极低的表示方法中挑选一个,尖峰表示无疑是首选。在CMOS技术中,什么会消耗能量呢?答案是线路切换。假设我需要表示一个介于1和128之间的整数。在尖峰表示中,如果平均表示,比如在64这个数值上,我必须切换这条线路64次。然而,如果我选择使用7位整数来表示0到128,我拥有7个位,其中大约一半会发生翻转,而不是切换。这样一来,就只需要翻转3.5次。比较一下,这就是1.75次切换与64次切换的差距。因此,尖峰表示与整数表示相比,能量开销高达32倍,这显然不是一个理想的选择。
再来看模拟表示。关于模拟表示,我有一整套的论述来解释为什么它在执行单个操作时表现良好,但在系统级别上却不尽如人意。不过,为了简洁起见,我就不深入探讨了。简而言之,无论是存储还是移动模拟信号,通常都需要将其转换为数字信号。然而,这种转换会消除你从模拟操作中获得的任何优势,因为并没有简单直接的方法来存储或移动模拟信号。
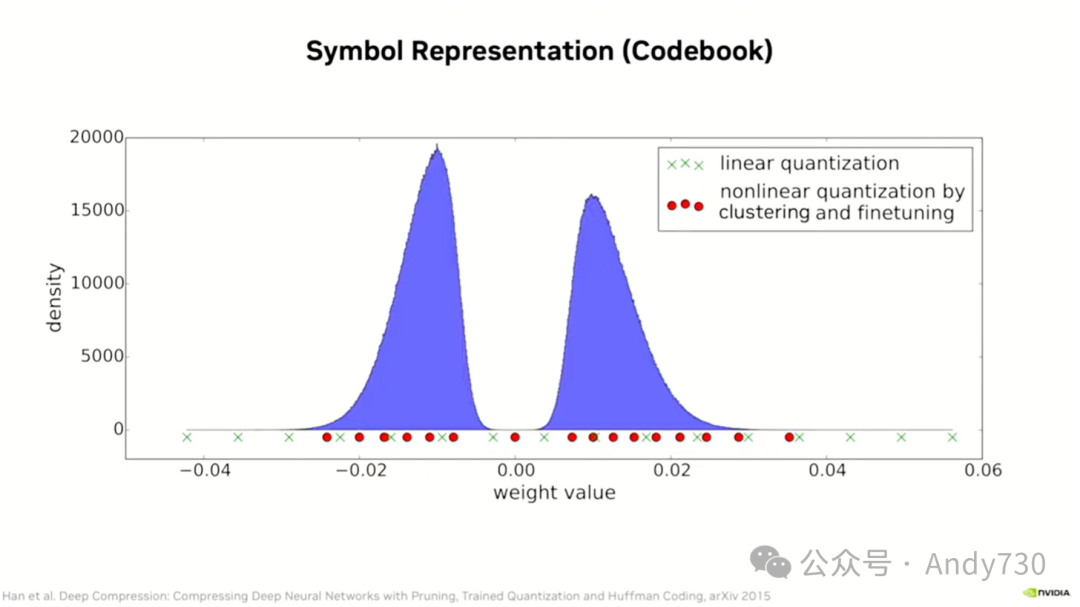
现在,让我们来谈谈表示和分布。如果你对网络进行剪枝,或者利用稀疏性,你可能会得到一个双峰分布。这实际上是我2015年那篇ICLR论文中的权重分布图。如果你选择线性量化,也就是基本上只使用整数表示,并且你有16个值,它们将会出现在X所在的位置。你可以看到我在这里有很多取样点,而那里几乎没有什么。在整个分布的叶下,我只有像三个X这样的点。因此,我将会得到非常高的误差。然而,如果我训练码本,我得到的小红点将会更加集中,我基本上会把所有的点都放在它们表现良好的地方。事实上,这样做是最优的。你训练码本就是为了达到这样的效果。虽然有一个k均值聚类步骤,但除此之外,你基本上是在使用随机梯度下降来将这些码本条目移动到最佳位置。这就是你想要达到的目标。
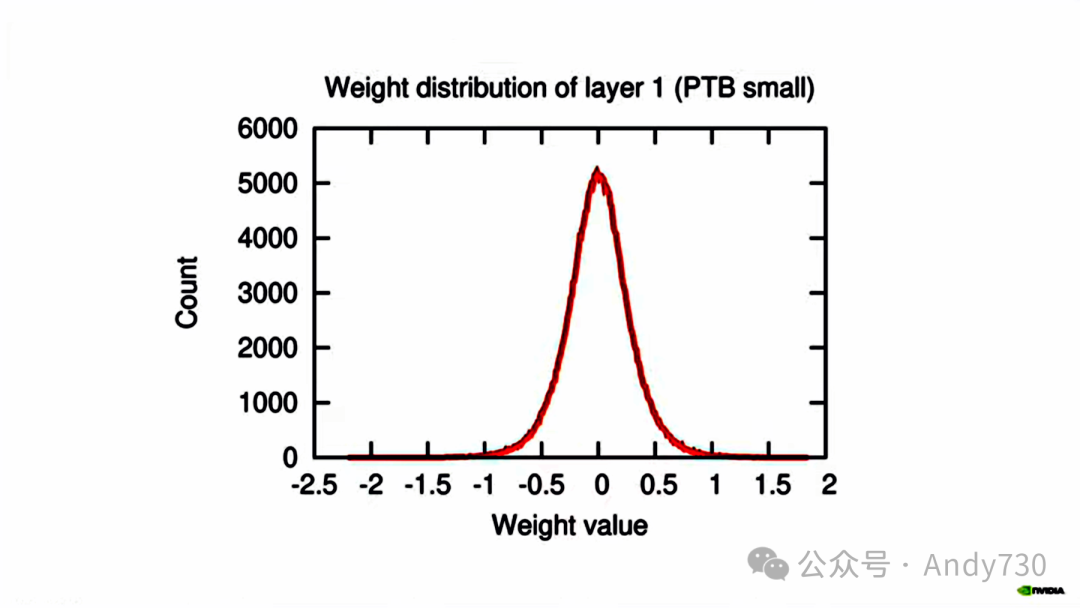
如果你不进行剪枝,你往往会得到这样的分布。这里要理解的重要事情是,你大部分的值都接近零。因此,非常重要的是要很好地表示小值。因为小值的误差往往比大值的误差权重更大,因为小值的数量并不多。

接下来,我们谈谈对数表示法。

对于我们这一代人来说,上大学时,我们可能是在这样的工具上进行数学计算的。这就是计算尺,它主要进行对数运算。上面刻的小线代表了对数间隔。例如,我要计算1.12乘以1.2,只需将1.12放在这里,移动到1.2的位置,然后读出答案。实际上,我将乘法运算转化为了加法运算。我计算的是线性距离,同时利用刻度线上编码的对数表进行数学计算。与整数或浮点数表示法相比,对数表示法具有出色的特性。

如果我选择对数表示法——这里,我正在使用我所说的8位对数4.3表示法。其中包含一个符号位,7个指数位,其中4位在二进制点的左侧,3位在右侧。这意味着,如果你将这些位串联起来,你实际上是在计算2的某个幂次除以8。在二进制点的右侧需要有一些数值,因为如果只考虑2的幂次,它们之间的间隔会过大。你的数字系统需要更细致的分级。通过移动二进制点,你可以在精度和动态范围之间找到平衡。
与FP8相比,我选择了E4M3,即4位指数,然后取相同的3位,但不是扩展的指数,而是尾数值。在这里,我们拥有相同的动态范围,因为我基本上选择了相同的指数。但我的最差情况准确性提高了50%。稍后我会给你一个图表来展示这一点。基本上,我是按块值来缩放误差的。每个具有相同指数的块具有相同的误差,然后跳到一个更大的误差,而对数表示法则是对每个值都进行了缩放。因此,最小数字的误差非常小。
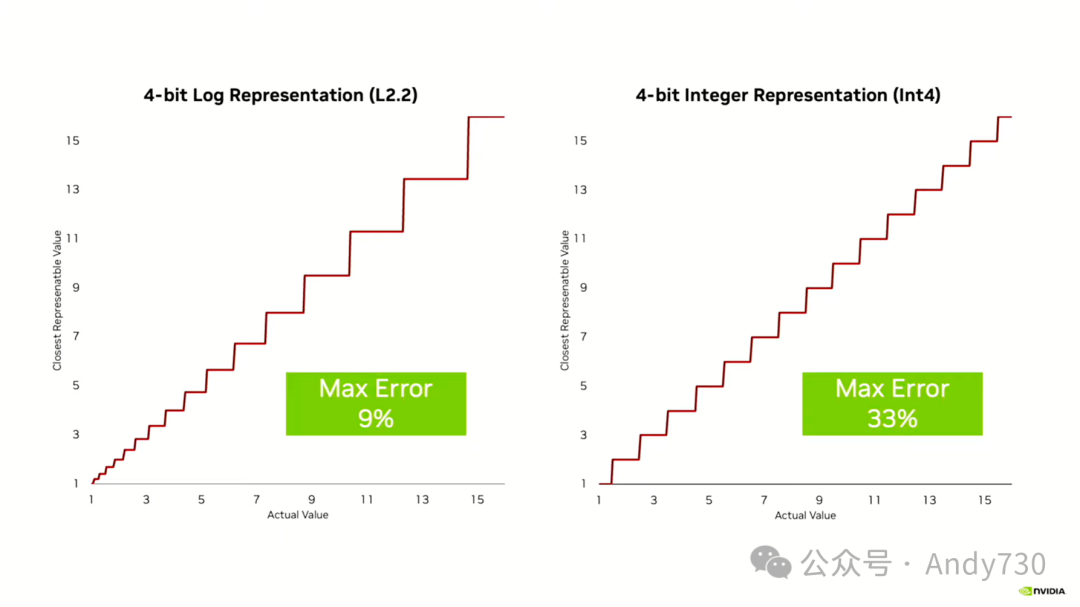
这里是对数表示与整数表示的比较。你可以清晰地看到,对数表示法的优势在于表示较小的数字,而这恰恰是我们最为关心的部分,因为大多数权重都集中在这个范围内,其误差非常小。在1.5左右的最大误差,无论是向上还是向下调整,都大约是9%。这是使用4位对数2.2(无符号位)时的情况。而使用4位整数表示时,这里的最大误差高达33%,因为误差的绝对值是一样的。在任何位置,误差都是0.5。所以,在1.5或15.5这样的数值上,误差同样是0.5。这意味着,在我们真正关心的区域,整数表示法会带来非常大的误差,而且这种误差是不成比例的。
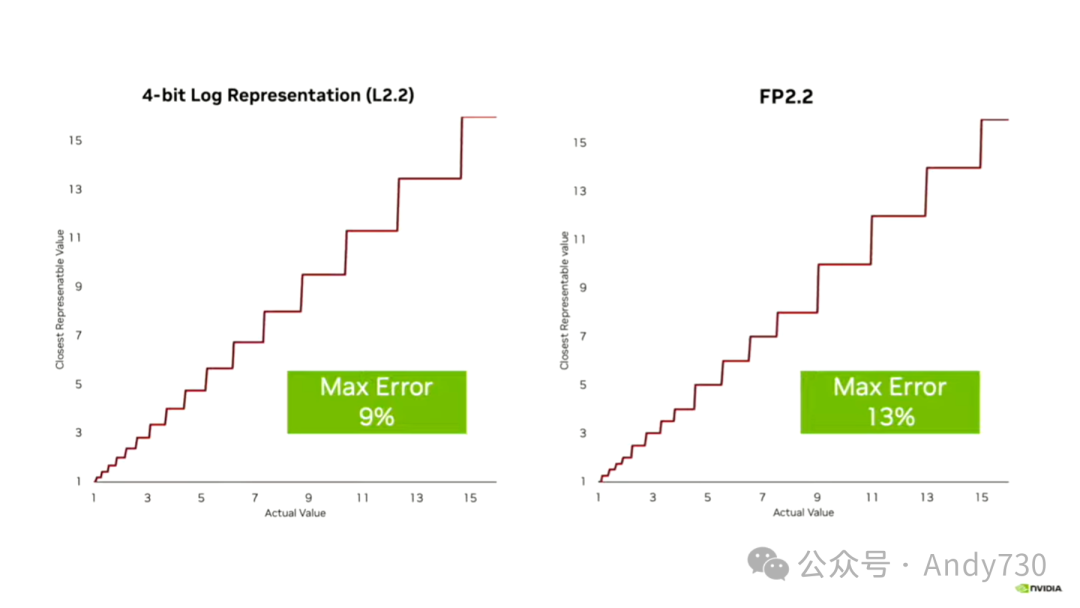
浮点数在某种程度上可以被视为一种不那么理想的对数表示。这里我们比较了浮点数2.2与对数2.2的误差。你可以看到,误差增加了一半,从9增加到了13。这是因为,在使用浮点数时,你对前四个步骤使用了相同的步长,接着对接下来的四个步骤也是如此。而在使用对数表示时,你在每个元素中都增加了步长。因此,你最终得到的误差更小,这在表示最小值时尤为重要。

对数数字系统有哪些特性呢?首先,乘法运算变得非常高效,因为只需进行加法运算。实际上,与在整数或浮点数系统中进行乘法相比,加法运算的成本要低得多。在整数或浮点数系统中,乘法是一种二次成本的操作,而加法则是一种线性成本的操作——与位数成比例。然而,加法在对数数字系统中并不容易实现,因为通常需要进行查找操作。所以,具体性能还取决于绿色区域(EI和EF)的转换效率。
EI只是一个简单的移位操作。你取得那个指数,它告诉你需要移位多远。然而,EF则需要一个查找操作。你必须在八个值中查找一个,这些值都是2的幂——2的0次方很简单,就是1。但接下来是2的1/8次方、2的1/4次方、2的3/8次方、2的1/2次方等等。你需要查找这些值的二进制表示,并用足够的位数来表示它们以保持准确性。然后,根据EI的数量进行移位操作,再进行加法。如果每次加法都这样做,那将是一个非常耗时的操作。但想象一下你在深度学习系统中做的事情。你通常在进行大量的乘法运算,并将所有结果相加来计算新的激活值——实际上,通常是成千上万次的乘法,然后将它们全部相加。
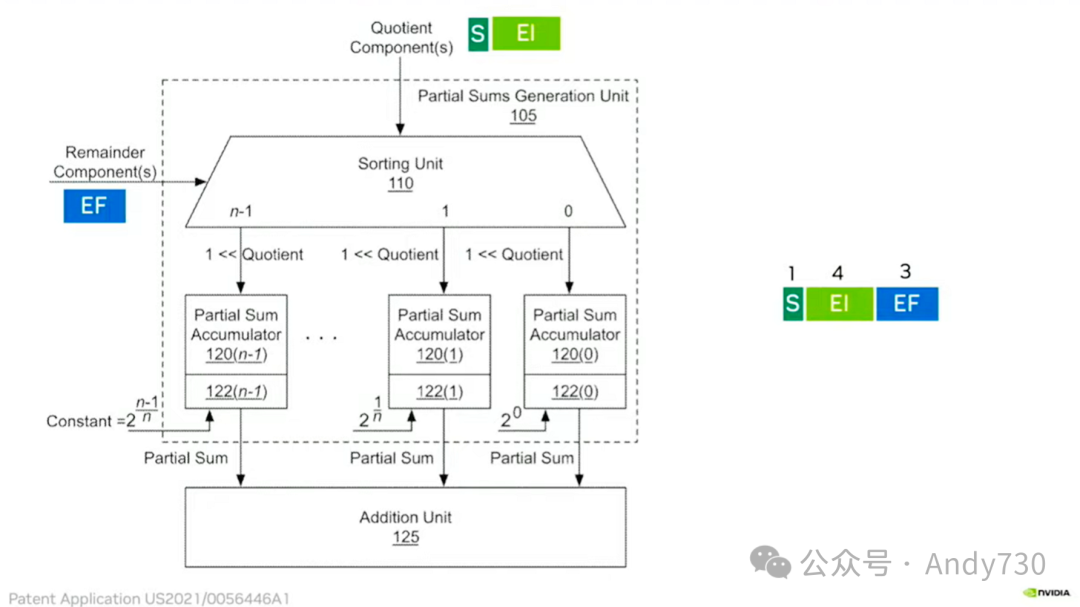
这里有一个来自某个美国专利申请的图。数字在下方,展示了如何以低成本进行这种操作。你需要做的是将这个表查找操作移到这10,000个元素的外部。假设我有10,000个元素要相加,每个元素都有EI和EF。我根据EF对它们进行排序,EF可能是2的1/8、2/8、3/8或1/4。我需要在最后乘以它们吗?我取所有这些元素,并将它们的整数部分相加在一起,这很简单。然后,如果我取余数部分,也就是EF部分,并在排序单元中选择——假设它是三位——我将指向由商部分确定的八个输出之一。在典型的应用中,不是每个周期处理一个元素,通常是每个周期处理8或16个元素。然后,我传递符号和EI,我取得符号位,并将其移位到商。接着,我将这些累加器相加。这是一个热和求和的过程,你可以利用它,因为你只翻转了一个位。如果你足够聪明,你可以利用这一点来提高能效。我将所有这些元素相加,直到我完成整个张量的计算。
完成了10,000次加法运算——平均每个区间大约1,000次。然后,我进行一次查找操作。实际上,这不是真正的查找操作。它是硬连线的。我将那个常数硬连线到这里。我用这个硬连线的数字进行最后的乘法运算,取出部分总和,然后将它们相加。现在,我得到了整数形式的值。而且,有一种非常简单的方法可以将其转换回对数形式。这就是对数数字系统的运作原理。

接下来,我们将讨论如何最优地裁剪你的数字。

这实际上是一个关于如何选择适当的动态范围的问题。不论你采用哪种表示方式,无论是整数、对数还是浮点数,关键的操作是如何确定一组数字的可表示范围的居中位置。简单来说,你必须表示分布。
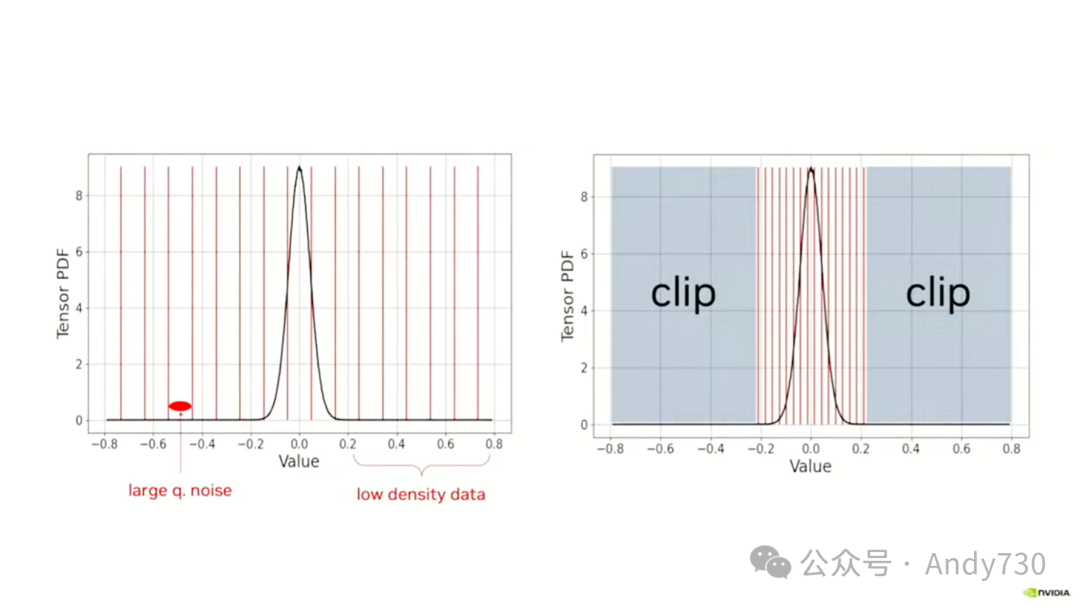
让我介绍两种可能的做法。
首先是大多数人目前采用的方法。你基本上会扫描——假设我有一堆权重或激活值。我扫描我的权重或激活值,并且可以在不同的粒度上执行此操作。稍后我会谈到这一点,通常是对每一层进行一次操作。所以,我会选择网络的一层,扫描所有权重,比如找到最小权重-0.8和最大权重0.8。然后,我会调整我可表示范围的数字——在这种情况下,它是一个整数表示,因为它是均匀分布的——以便我可以精确地表示最大值和最小值。这样,你就不会遇到任何剪辑噪声。通过限制较大的数字,我不会产生任何噪声。但我的量化噪声会非常大。这些红色条之间的间隔非常大。
另一方面,我可以选择进行裁剪。我可以选择说,与其表示0.8,我将我的最大可表示数字设为0.2。这意味着我必须将这里的任何数字都限制在0.2以下。这将引入剪辑噪声,降低这些数字的值。但我的量化噪声会小得多。
在某次会议上,我提出了一个有趣的问题,我认为这个问题很难回答,那就是是否存在一种方法可以找到设置这个剪辑因子的最佳位置,以便获得最小的均方误差。虽然这并不是你真正想要的,但它是一个很好的代理,也是一个可以明确表述的问题。你真正想要的是神经网络中的最小误差,但那是一项更具挑战性的任务。
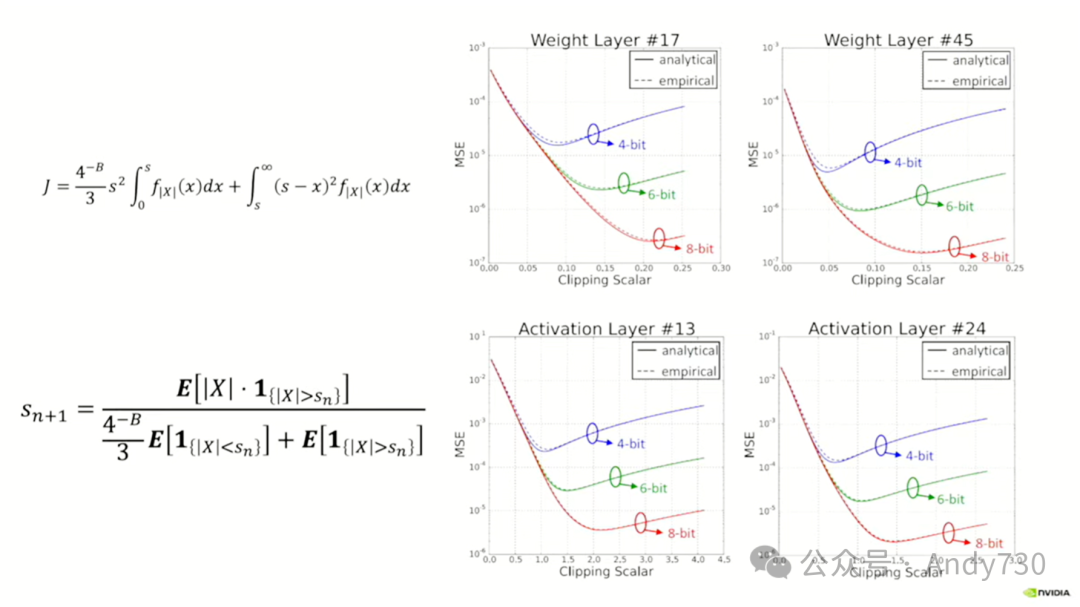
然而,我们团队中最近加入的一位员工在一个小时内就解决了这个积分问题。他告诉我:“是的,你只需要解决这个积分。”我对此感到相当震惊。
听众问:GPT-4或? Bill Dally:不,这是在GPT-4之前。他实际上亲手解决了这个数学问题。我必须说,这真的令人印象深刻。解决那个积分是相当困难的,你可能不会希望每次针对变化的激活函数都这样做。
然而,有了这个迭代方程,我们可以近似这个积分,而他在大约一天后就给出了结果。如果你进行2或3次迭代,它可以为你提供一个非常接近真实积分的值。这个方程还给出了上下裁剪点。直观地来说,让我们看看这个例子。这是一个特定的层,我们正在查看的网络的第13层。假设我使用四位数字来表示。如果我的裁剪比例尺在这里,那就意味着我没有进行任何裁剪。我可以表示直到4.2或其它最大可表示的值。因此,当我开始裁剪时,我的噪声会减少,因为我大大降低了量化噪声。而且,我实际上没有引入太多的裁剪噪声,因为在这个范围内几乎没有权重,直到我移动到大约这里的这一点。在这一点上,我达到了一个最小值。如果我再降低裁剪比例,裁剪噪声开始变得足够大,以至于实际上使整体的均方误差增加。但这就是我想要的位置。如果我查看误差的点,我这里没有5位数线的具体数据,但实际上我最终得到的误差远低于5位数线的顶部。事实上,如果我没有进行任何裁剪,我的误差几乎达到了6位数线。因此,在减少均方误差方面,这样做是非常值得的。所以,最重要的不是按照你认为的方式进行缩放,而是找到最优的缩放方式来最小化均方误差。
听众:这个假设是基于一个预先训练好的网络,你进行裁剪。如果在训练循环中,你实际上假设在训练期间有一定数量的表示形式,那么这个答案会不会有很大的变化?
Bill Dally:这是一个很有深度的问题。实际上,我并不确定它是否会有很大的变化。如果能够训练裁剪因子,那将会是非常理想的情况。
听众:好吧,为了得到可能最简单的结果,这里确实有很多需要权衡的地方。
Bill Dally:我很高兴你这么认为,因为我自己之前也没有深入考虑过这个问题。但我认为,理论上讲,我们是可以训练裁剪因子的,只需要将反向传播应用到裁剪因子上。然后,其它的权重将会根据裁剪因子进行调整。目前,我们是在训练完成后再进行这个操作的。实际上,我们并没有用剪辑重新训练网络,尽管这样做也是可能的,而且可能会得到更好的效果。
听众:我想更广泛地探讨一下,是否可以选择最简单的数字表示形式,以便在可能的任何合理动态范围内,以及你所描述的分布中的任何极端特性下,都能得到理想的效果?我假设这是你目前唯一可用的数学方法,所以—— Bill Dally:我们仍然需要选择一个scale factor。关键在于,你不仅仅是使用表示形式本身,而是结合一个scale factor来使用它。这个scale factor的选择变得尤为关键。

因此,让我再深入谈谈向量缩放。实际上,向量缩放可能是这次演讲的核心信息。在通常的实践中,我们都会进行缩放。当我们开始缩放时,需要两个缩放因子,一个用于前向传播,另一个用于反向传播。这是因为两者最终使用的值可能会有很大的差异,特别是在反向传播中,你需要乘以一个学习率,这会使返回的数字变得更小。然后,我们会逐层进行缩放。如果你发现某种方法有效并改善了结果,你可能会想是否可以进一步优化?
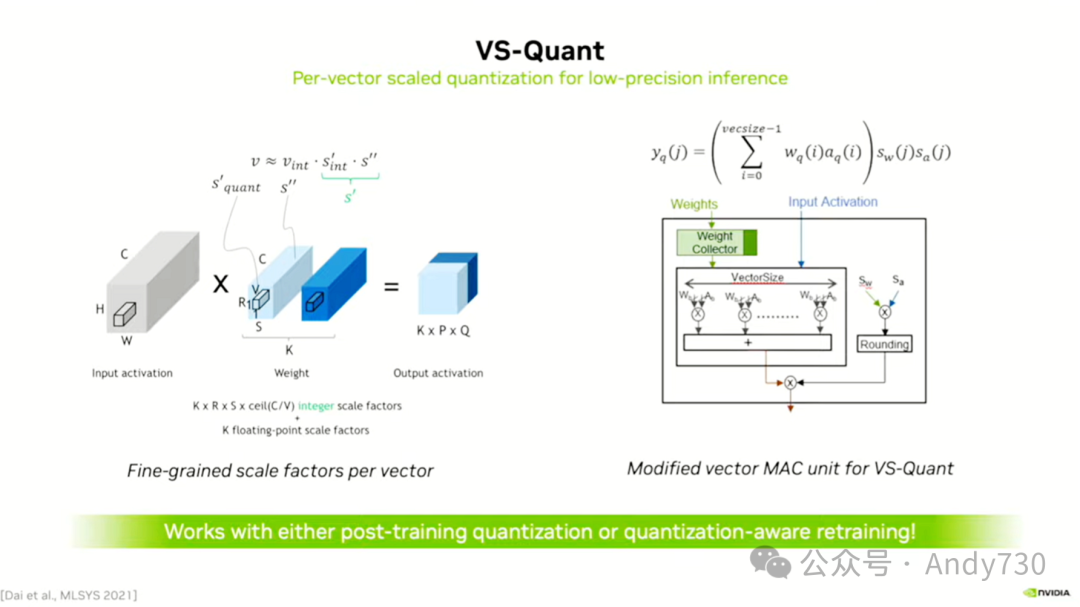
于是,我们转向了更细粒度的缩放。这进一步提升了效果。于是,我们提出了一个问题:如果我们不是按层进行缩放,而是按矢量进行缩放,效果会如何呢?这里的‘矢量’指的是包含16、32或64个元素的集合。由于每个矢量都有一个非常紧凑的分布,我们可以对其进行缩放,从而获得非常出色的结果。这实际上相当于增加了额外的精度位数。
因此,我们的思考方式是,在常规操作中,你会按照这里展示的方式处理ConvNet。我们有一个维度为高度乘以宽度乘以通道数的张量,即 H、W 和 C。接着,我们通过 R 乘以 S 进行卷积,这里的 R 和 S 是卷积核的大小。但在通道维度上,我们会使用对应通道的权重进行点乘操作。
假设我选取一个在通道维度上长度为32的矢量元素,并与该元素进行点乘,我可以独立地对这个32元素矢量进行缩放,而不影响张量的其它部分。为了实现这一点,我最终在我的 MAC 单元中添加了一个小单元。在输出端,完成所有权重与激活函数的乘法运算以将其转换回预缩放数字之后,我必须乘以两个缩放因子——一个用于权重,一个用于激活函数,即 sw 和 sa。
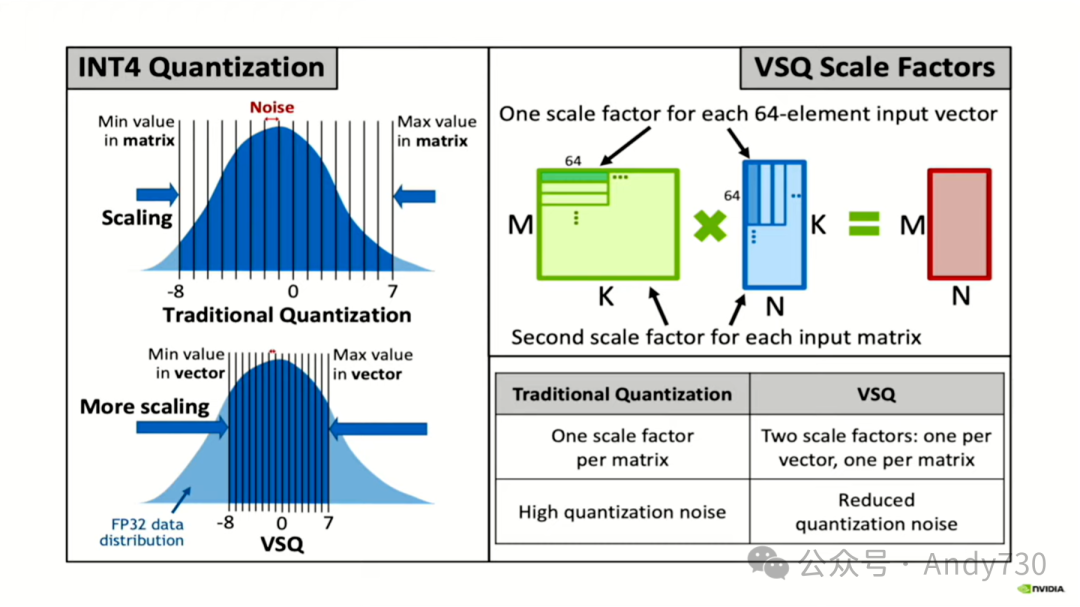
从图形化的角度来看,我们可以这样想象:这个大蓝色块代表整个层的分布,而这条线的小范围则代表我的矢量的范围。因此,现在基本上我在对一个更小的矢量进行缩放。
如果我对这个更小的矢量进行最优裁剪,我可以获得更好的效果。因此,这个方法在实际应用中表现非常出色。接下来,我将展示我们构建的一款加速器的一些实验结果。

让我先谈谈稀疏性。
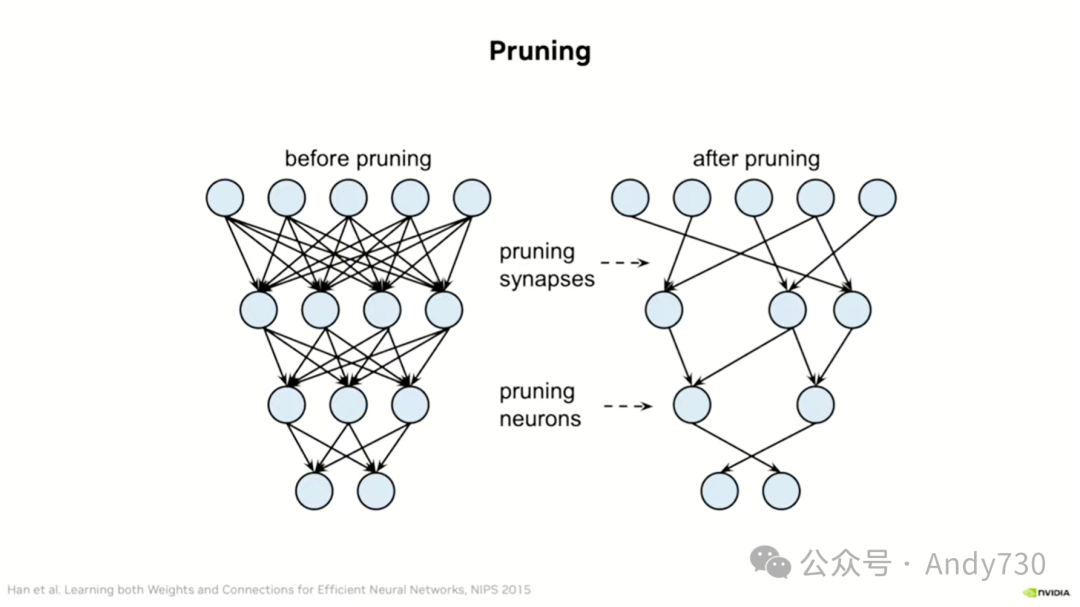
这张图来自我和宋于2015年在NeurIPS(当时称为NIPS)上发表的一篇论文。在这篇论文中,我们展示了一个实验:取一个神经网络——这里展示的是一个多层感知器——删除其中一部分权重,然后使用掩码重新训练它。这个掩码的作用是保持被删除的权重不变。最终,我们几乎得到了与原始网络相同的准确性。
实际上,对于多层感知器,我们可以删除高达90%的权重而仍能保持相同的准确性。而对于卷积神经网络(ConvNets),这个数字通常更接近30%。也就是说,你可以删除60%到70%的权重,使网络的密度保持在30%到40%,同时仍然保持相同的准确性。我们觉得这一发现非常有趣。
为了进一步验证这一发现,我们实际上设计了一个小型测试条带,名为“高效推断引擎”。这个引擎的目的是展示我们如何在实际应用中实现稀疏计算,并且这种计算方式是高效的。与标量引擎相比,我们的高效推断引擎具有更高的效率。为了实现这一点,我们使用了专用硬件来遍历CSR结构,从而能够在50%的密度下有效地进行稀疏计算。
我记得原始论文的一个审稿人曾经评论说,这只是学术上的好奇,因为大家都知道,如果使用稀疏矩阵包,那么矩阵的密集度必须非常低,比如不超过0.1%,否则直接运行它会更快。确实,如果全部在软件中进行稀疏计算,那么审稿人的观点是正确的。但我们的方法有所不同。我们基本上为CSR指针分配了单独的内存数组。我们还设计了特殊的硬件来遍历这些内存数组。因此,我们的稀疏计算几乎没有额外的开销。
问题是,实际上没有多少人愿意去做标量计算。为了进行比较,我们构建了一些最先进的加速器,它们配备了并行向量单元。这些加速器基本上可以同时执行16个长向量的运算,每个周期可以完成256次乘法。现在,我们面临的挑战是如何在稀疏情况下使它们高效工作。
自2015年以来,我一直在努力解决这个问题。我不断尝试提出新的想法,看起来都非常不错,直到我们实际去合成逻辑。然后,我发现了一个问题:如果我想对两个稀疏向量进行点积运算,并在最后一刻筛选出非零元素并将它们送入MAC单元,这会产生大量的闪烁。这是因为多路复用器在实时尝试判断哪些数字是0。它会不断选择这个数字,然后说:“不,这个数字在这里是非零的,但在另一边它是0,所以让我们把向量移到下一个位置。”最后,为了每个计算,它们会切换数学单元5次,这极大地消耗了我们的能源。
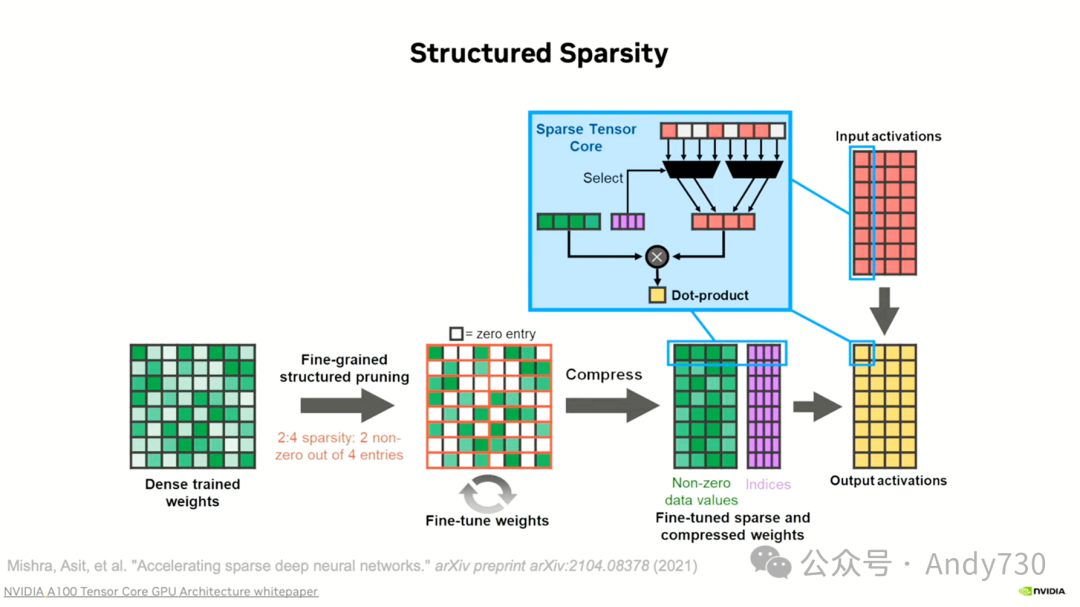
因此,我们一直在寻找消除闪烁的方法,因为这成为了许多稀疏运算的瓶颈。在Ampere和Hopper中,我们都找到了一个有效的方法,我们称之为“结构化稀疏性”。原来,稀疏性之所以难以处理,是因为它是不规则的。当数据不规则时,我们需要花费大量精力去整理它们,使它们到达正确的位置。
我们的解决方案是避免不规则性。我们强制使稀疏性具有某种规律模式。具体的方法是,和所有与稀疏性相关的工作一样,我们密集地训练网络。即使对于所有的稀疏性,大部分的训练也是在稠密的情况下进行的推理。但是,在训练完网络之后,我们会找到最低的权重并将它们删除。但在这里,我们会以结构化的方式进行删除,即我们坚持要求每四个中最多只有两个是非零的。如果你做不到这一点,那么你可能只能进行密集计算。但是,如果你能剔除四分之二的权重,这通常是可以做到的,特别是当处理MLP时,你可以剔除10个中的9个。那么,剔除四分之二应该就很容易了。
我们将这些权重删除,然后使用掩码重新训练网络,使其它部分在某种程度上补偿消失的部分。接着,我们通过仅存储非零权重和一些元数据来压缩模型,这些元数据告诉我们哪些权重被保留了。由于元数据是静态的,不会频繁变动,我们将其输入多路复用器,用于选择输入激活。具体来说,如果我们有八个输入激活,而元数据告诉我们其中四个是非零的,我们就选择这四个并将其馈送到乘法器中。这样,我们得到了一种规则性很强的计算方式,效率几乎翻倍。目前,我们正在研究如何将这种方法扩展到激活函数上,以及如何结合两种稀疏模式,同时保持计算的可预测性。

接下来,我简要谈谈加速器和加速器与GPU之间的关系。
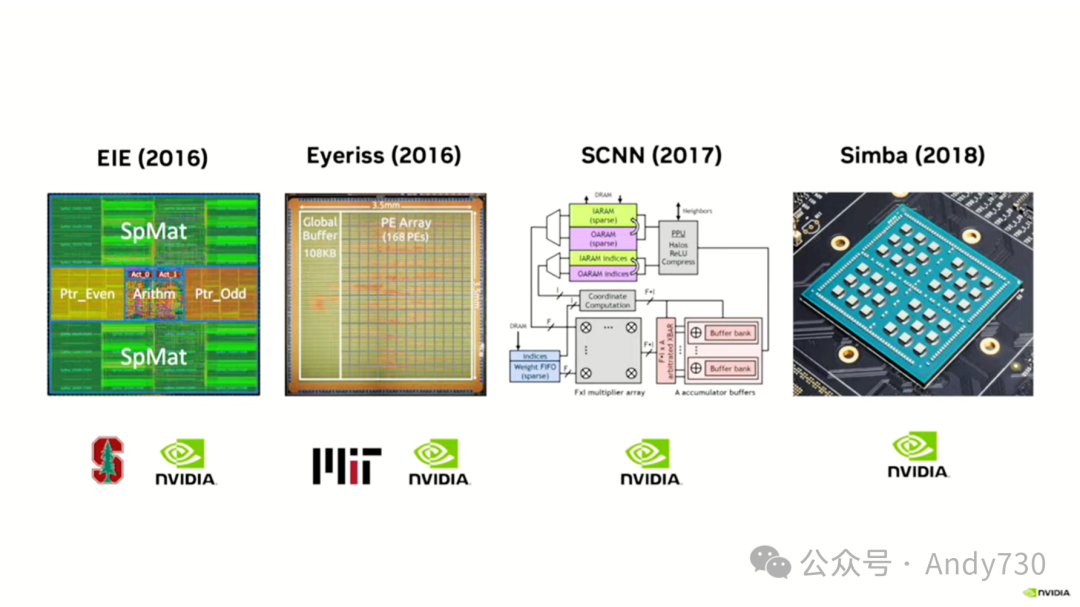
我们在NVIDIA开发了一系列加速器,其中EIE是与斯坦福大学合作完成的,而Joe Lemar则在NVIDIA与麻省理工学院合作完成了另一项工作。我们还开发了用于稀疏卷积神经网络的SCNN加速器,以及多芯片模块等。

这些加速器之所以能获得出色的性能,主要有五种原因。
首先,它们采用了特殊的数据类型和操作符。这与我们从GPU中借鉴的经验有关。我们针对数据类型进行了专门化设计。以Hopper为例,它采用了FP8数据类型,并使用QMMA专门处理FP8的8x8矩阵乘法。通过这种方式,我们基本上用一个周期完成了原本需要数十或数百个周期才能完成的工作。因此,QMMA和IMMA都能在单个指令周期内完成1024次操作。
其次,这些加速器具备大规模的并行性。我们追求的是1000倍的性能提升,因此希望大量的计算单元能够并行工作。在构建加速器时,优化存储器是非常重要的。主存储器访问成本高昂,如果频繁地从主存储器中读取数据,性能将会受到限制。由于深度学习涉及多个层次的读取,我们可以通过使用小的暂存区来实现良好的数据重用。
当我们为生物信息学设计了一个加速器,并在Hopper中实现了动态规划指令时,我们首先考虑了生物信息学算法——Minimap,这是广泛使用的算法。我们提出了一个问题:如果只为这个算法设计专用硬件,我们能获得多少加速效果?答案大约是4倍。就在我们准备放弃并转向其它项目时,我们想到,如果重新设计算法呢?这引出了算法、架构和代码协同设计的挑战。
事实证明,生物信息学家认为动态规划计算成本高昂,因此他们花费大量时间在种子阶段,试图找到好的候选项以进行对准。而我们采取了不同的策略:我们使对准阶段变得非常高效,因为我们的对准引擎比CPU上的对准操作快150,000倍。而种子阶段相对昂贵,因为它需要主存储器访问。因此,我们颠倒了这一策略,设计了一个非常经济的种子阶段,其中可能产生大量误报输入到对准阶段。但由于对准速度极快,它能够自我过滤,最终我们实现了大约4000倍的总体加速。
然而,关键在于优化内存访问。你不能一直依赖主存储器进行引用并期望获得良好的性能。此外,减少操作的平均开销也很重要。对于简单的操作,与CPU相比,我们的加速器可以实现10000倍的加速。

我一直在从事这方面的研究,从1985年开始的快速加速器设计。我最初是从事仿真加速器的设计,之后涉及信号处理,最近则是神经网络和SAT求解器。

我想强调操作开销的重要性。这是一篇关于简单ARM乱序核的论文中的数据,尽管它是相对简单的核之一。我忘记了具体是哪个型号——可能是某种A型号,我以为我在这里写下来了。然而,与我们今天拥有的更先进的核心相比,例如Grace芯片中的Neoverse核心,这是一个非常高效的CPU。但即使如此,执行一个CPU指令的成本仍然很高。即使那个指令是一个空操作,获取指令、解码、进行分支表查找以及在寄存器文件中进行乱序操作的成本是250皮秒焦耳。而执行一个16位整数加法的成本是32飞秒焦耳。所以,大部分开销都来自于指令执行的辅助操作。因此,我认为在设计和优化硬件时,需要密切关注这些开销,并努力减少它们。
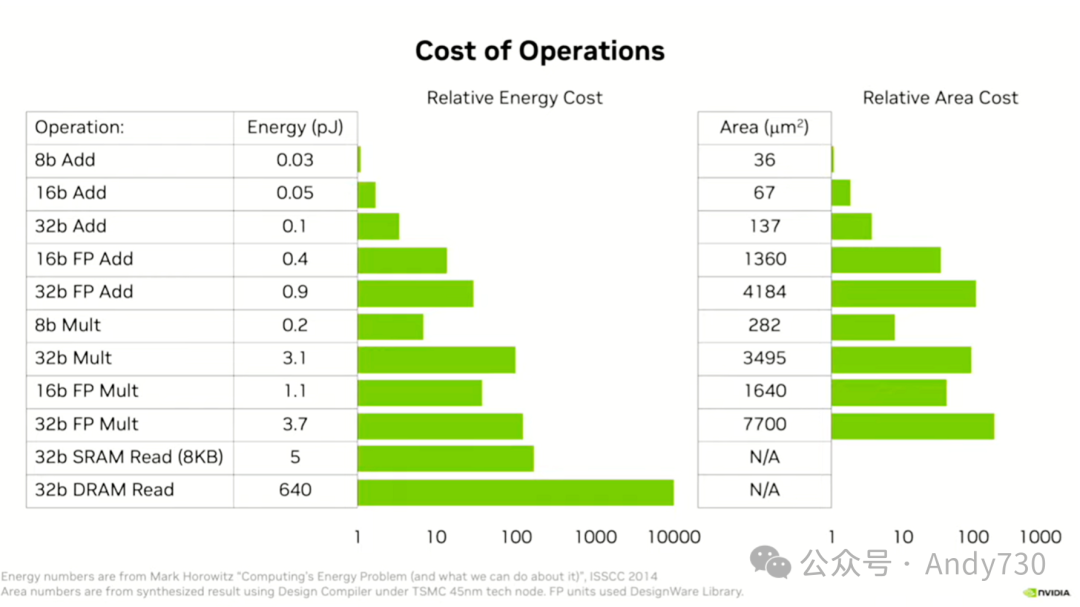
在乘法运算方面,存在二次扩展现象。一个32位乘法的成本并不仅仅是8位乘法的4倍,而是比8倍还要贵,实际上是贵了16倍。浮点数的情况稍微复杂一些,但大致相同。其中还涉及到一个特殊的归一化阶段。你会发现,从内存中读取数据的成本比所有这些操作都要昂贵,甚至比32位乘法还要贵。读取一个相对较小的8k字节内存的成本更高。读取内存的距离越远,情况就会变得更糟。
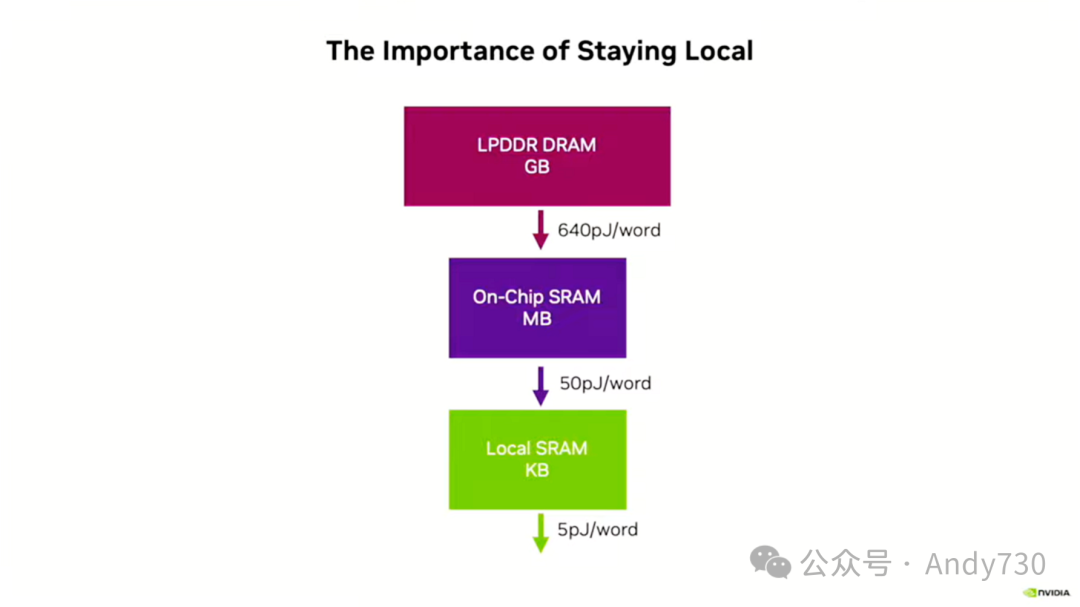
我喜欢使用这种数量级的方式来描述,例如,如果我读取一个本地的8k字节内存,每个字的成本是5皮焦耳。如果我必须穿过芯片并读取,基本上是数百兆字节的内存,每个字的成本是50皮焦耳,但其中的内存部分仍然是5。你使用小内存阵列来构建大内存。因此,我们基本上有一个内存阵列大小,我们倾向于用于所有东西,因为在一个位线上,你只能有那么多位单元,在一个字线上,你只能有那么多单元。所以这是你的基本阵列大小。超过这个大小的任何东西都要使用多个阵列。所以另外的45皮焦耳是通信能量。这是将地址传送到内存阵列并将数据传送回来的成本。然后,如果你离开芯片,情况就会糟糕得多。LPR,这是你能得到的最节能的DRAM——实际上与HBM相当。现在,它大约是——我在试着回忆——大约是每比特5皮焦耳。读取32位字,这就是为什么这样,是640皮焦耳。
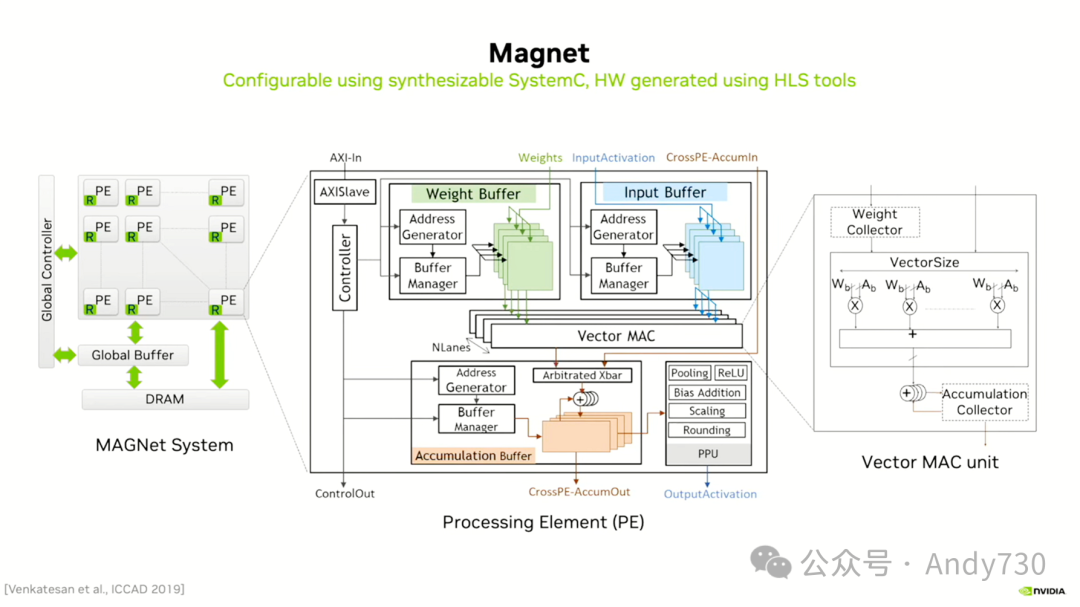
接下来,让我来谈谈我们最近的一个最新加速器项目。我们从一个程序开始,实际上,它搜索加速器的设计空间。我们基本上给它我们的目标神经网络,然后我们说,对于加速这个神经网络,最好的加速器是什么?它搜索一堆参数——有多少处理单元。我们有这个向量MAC。我们有一堆向量MAC的通道。所以这是一个二维的东西,有很多向量和很多向量元素和很多通道——不同缓冲区的大小将会是多少。因此,它在搜索有限的设计空间。我们有一个有点风格化的东西,但它在变化所有的参数。它实际上可以将多个级别放入我们通过的scratchpad层次结构中。
在ICCAD的论文中,我们实现了大约每瓦特20万亿次的8位操作,你会意识到——这在技术上比Hopper落后一代。我认为是在12纳米工艺,而Hopper是在5纳米工艺——实际上,所以它是两代技术之后。但我们仍然做得比较好,因为我们优化了很多东西,并且我们可以将这些应用到Hopper上。

更进一步的是,我们今年在JSSC上发表了一篇论文,而去年则是在VLSI电路研讨会上发表了关于Magnetic BERT的研究成果。因此,我们完成了两项工作。我们计划将其应用于LLM,因为它正成为当下的热门话题,而非ConvNets,MAGNe真正优化了这一点。另一方面,我们也想应用我们所有关于最佳裁剪和向量级别缩放的学习成果。因此,它支持向量级别的缩放。我们增加了额外的两组乘法器,用于乘以激活和权重,以及缩放因子,使其能够在基于32个元素的向量上运行。这使得我们能够运行一种特殊的量化方法,我们称之为VS-Quant INT4,而且可以在不损失精度的情况下运行BERT和BERT Large。因此,我们能够通过最佳缩放实现4位量化的推理。
在这个图表中,真正重要的数字——虽然我不会详细解释——是每特拉操作95.6瓦的能耗。因此,我们几乎每瓦能够达到100万亿次操作,比Hopper的效率提高了约10倍。而且这是在相同的工艺下实现的。顺便提一下,我们在NVIDIA进行原型制作的方式是,等待有人发送这些大型800平方毫米芯片之一,然后我们会说:“好吧,你有800平方毫米的空间。显然,我们可以从你那里借用一个毫米的角落。”这有点像坐在那里向别人借你的杯子用一下。我们会问:“我可以要一个毫米的空间吗?”他们通常都会同意。因此,我们最终在一个大型GPU上启动了这种实验之一,我相信这是Hopper交换芯片,并回来——这些是实验室的数据——效果非常好。我们能够在上面运行BERT并取得出色的结果。因此,我认为这是我们希望在未来一些GPU中投入的原型,并显示出我们有另一个比Hopper高10倍的因素要追求。

好的,让我总结一下,并回答一些问题。
深度学习是通过硬件实现的,并且受到硬件的制约。算法和数据在之前的几年里已经存在,它们就像是GPU的火花所需的燃料-空气混合物。它拥有足够的能量和马力,在足够大的数据集上以合理的时间训练出足够大的模型。
从那时起,我们的训练需求增长了10的8次方倍,在petaFLOP天数方面,从AlexNet的10的负2次方增长到了GPT-4的10的6次方。为了应对这一挑战,我们不得不提高GPU的性能。在过去的10年里,GPU性能提升了1000倍,而剩下的10的6次方倍的增长则来自于时间和GPU数量的增加。现在,人们使用近10万个GPU的集群来训练这些大型模型,并花费了几个月的时间。这确实是一个巨大的投资,但人们正在获得证明其价值的结果。
那么,我们将从哪里继续前进呢?我之前已经提到了一些内容,尽管我没有过多地讨论稀疏性,因为我们对稀疏性还没有一个明确的答案。然而,我仍然认为,未来最大的收益将来自于找到如何比我们现在从稀疏性中获得的2比1更好的方法。当然,在数字方面还有很多工作要做。我谈到了对数数字,它们在本质上比整数或浮点数更具优势。虽然浮点数很接近,但对数数字通常具有最坏情况误差,这种误差比FP的最坏情况误差要小约33%,因为每一步都经过了缩放。
最佳剪裁是一个巨大的收益。在选择scale factor时,需要非常谨慎。我不知道最小均方误差是否真的是最佳的度量标准,但它是一种容易量化和应用的度量标准,并且我们在此基础上取得了良好的结果。当进行缩放时,需要选择缩放的粒度。为每32或64个元素分配一个scale factor并不会带来太大的成本。然后,可以缩放更小的数字组,使范围更加紧凑,从而减少误差。
接下来,我们构建了一系列加速器来验证这些想法。我分享了其中的两个:MAGNe和Magnetic BERT。Magnetic BERT的表现非常出色。它在BERT和BERT Large上实现了每瓦近100万亿次的操作,而且准确度几乎可以忽略不计。这对我们来说实际上是一个验证场,充分展示了向量缩放和最佳剪裁技术的优势。在进行这种算法硬件协同设计时,这种验证过程非常有益。我们正在努力探索如何——这总是需要一些时间和努力的。你设计了一个加速器,它只能完成一项任务。现在,我面临的问题是,如何将这个设计转化为未来一代GPU的指令?
----- 听众:你提到了稀疏性,我对目前正在使用哪些技术来优化网络大小很感兴趣。
Bill Dally:对,这实际上是一个不同的问题。对于网络大小的优化,我们有一个团队专门负责进行神经架构搜索。他们会在各种参数上进行搜索,例如层数、每层的通道数、层的大小以及它们之间的连接等。他们试图找到一个在某种优化定义下最优的模型。当然,模型越大,通常准确性就越高。但如果受到执行时间或功耗的限制,他们通常会尝试找到最小的模型以达到一定的准确度。这就是他们进行神经架构搜索的目的。
与此同时,他们还会进行网络修剪,这是另一个软件部分。我们实际上使用了几种不同的技术。最简单且被广泛使用的方法是扫描一层中的权重,并根据权重的大小进行修剪。如果你希望达到某个层的密度,它会进行直方图统计,找到那个点,并将所有低于该点的权重设为0。
我们还尝试了一种更复杂但效果更好的方法,尽管它更昂贵。这种方法试图计算每个权重的敏感度。它不仅关注权重的值,还关注与该权重连接的其它值对输出的影响。通过查看敏感度,它能够找到最不敏感的权重进行修剪。
这就是目前我们广泛使用的两种技术。
听众:我对于复杂的指令很感兴趣。你提到了节省了很多能量,这包括了提取和解码能量的节省,以及操作数加载的节省。我想知道你对这两者之间的能量分配有什么看法,以及。..
Bill Dally:我目前没有具体的分配数字。但我认为,在大多数情况下,提取和解码的能量节省可能会占据主导地位。不过,我需要进一步查找和确认这些数字。
听众:关于纵横交错的体系结构,Google的TPU与NVIDIA之间在这方面的设计确实存在许多人工差异。
听众:NVIDIA没有采用系统阵列来进行矩阵运算,是吗?
Bill Dally: 我们进行的是规模较小的矩阵乘法。当我们使用FP16或BF16时,我们的核心元素是一个4乘4的矩阵,而Google的TPU则倾向于进行规模较大的矩阵乘法。我不记得具体的尺寸了,但其中一个尺寸是128乘128。我们没有选择这种做法的原因之一是,它会导致碎片化问题。如果你选择了一个非常大的矩阵乘法作为基本元素,那么自然大小的矩阵可能并不是一个2的幂的整数倍。这可能会导致一些奇怪的情况。例如,如果你有一个4乘4的矩阵,你可能需要在某个地方四舍五入到3来适应它。但如果你有一个128乘128的矩阵,你可能会最终四舍五入到127,这将会非常耗费资源。然而,就矩阵乘法操作的效率而言,我认为我们做得更好一些。尽管我们没有使用系统阵列,但这并不重要。因为我们在进行矩阵乘法时,几乎所有的能量都消耗在数学单元中。实际上,只有一小部分,大约几个百分点,不在数学单元中。所以,采用系统阵列的方式并不会带来任何好处。问题在于,向矩阵乘法输入数据的能量成本是多少?我们可能会因为进行较小的矩阵乘法而有一些额外的成本。我们从寄存器文件中为矩阵乘法器提供输入。每次进行4乘4的运算时,我们都会进行一个264的寄存器提取——两个4乘4的矩阵。然后得到结果,再进行下一个4乘4的运算,依此类推。我们在进行更大的矩阵运算时,可能会有一些额外的洗牌开销,因为我们是以较小的颗粒度进行的。但即使这样,我认为这只是噪声,对总体性能的影响在10%左右。而Google仍然需要——他们仍然需要移动数据。他们必须将数据从任何地方移动到系统阵列的输入端。如果他们的成本低于10%,我会感到非常惊讶。他们还有控制开销。他们有一些小微控制器来告诉它,现在进行矩阵乘法运算,这也不是零成本。
听众:我想快速回到你之前提到的训练模型部分,你提到了查看数字和权重的分布,并对这些数字进行剪裁。我可能错过了一些细节,但我不太确定是因为硬件的改进使你能进行剪裁,还是因为软件或者像FPGA这样的可编程硬件。所以,在整个技术堆栈中。..
Bill Dally: 不,这几乎完全是软件实现的。我们已经有了可以使用的scale factor。这些scale factor让我们能够将数字缩放到适应我们数字系统表示的动态范围。传统的方法是选择一个scale factor,以便能够表示最大和最小的数字。通过剪裁,你只需要选择一个更大的scale factor。基本上,你将每个数字乘以一个较大的量。然后,当你将其转换为较低精度时,一些数字会被剪裁。我们使用饱和算术,所以这些数字会被限制在最大可表示的值。这主要是一种软件技术。唯一涉及到硬件的部分——而我们无论如何都需要它,因为我们在进行——如果你进行缩放,你必须要有——在右上角的那个小乘法器,表示sw乘以sa,将两个scale factor相乘,四舍五入,然后第二个乘法器——所以这两个乘法器必须被添加进去,每当你进行缩放时。但一旦你进行了缩放,你可以选择是否进行剪裁,以及任何你想要的粒度。你只需要为额外的scale factor的表示付费,如果你以更小的粒度进行缩放的话。
-
前OpenAI首席科学家创办新的AI公司2024-06-21 1220
-
聚焦黄氏定律:NVIDIA 首席科学家 Bill Dally 介绍推动 GPU 性能提升的关键因素2023-10-12 1332
-
NVIDIA 首席科学家 Bill Dally 将在 Hot Chips 大会发表主题演讲2023-08-22 1161
-
NVIDIA 首席科学家 Bill Dally 入选硅谷工程协会名人堂2023-02-11 1284
-
始于硬件却也被硬件所限的深度学习2022-12-05 974
-
NVIDIA将在中国多地设立研发实验室2020-12-16 2328
-
NVIDIA预测:GPU将推动AI性能逐步增长2020-12-15 2512
-
NVIDIA首席科学家Bill Dally将于GTC 中国线上大会首日发表主题演讲2020-12-11 1969
-
NVIDIA首席科学家Bill Dally公布了一个开源呼吸机设计2020-06-02 4198
-
百度徐伟宣布入职地平线 担任通用AI首席科学家2018-07-27 3420
-
NVIDIA深度学习平台2016-08-06 2301
-
NVIDIA首席科学家谈3D芯片、中国崛起2012-05-21 1045
全部0条评论

快来发表一下你的评论吧 !

