硅碳化物和氮化镓的晶体结构

晶体结构是通过原子（或离子/分子）群的周期性分布实现的。理想情况下，考虑一个在空间坐标中无限延伸的晶体，周期性转化为平移不变性（或平移对称性）。因此，整个晶体是通过一个基本单元的周期性重复生成的，这个基本单元称为单位格子，它可以包含原子/离子/分子/电子的群组，并且是电中性的。
 

 

平移对称性意味着属于基本单元的一般点与通过从第一个适当平移获得的基本单元的点一一对应。从数学上讲，整个结构可以由三个线性无关（因此不共面）的矢量（a1，a2，a3）生成。更准确地说，晶格的节点通过以下方式定位（相对于给定的笛卡尔参考Oxyz）

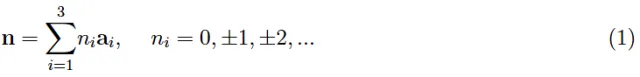
定义1：向量a1，a2，a3称为基本平移向量，而n类型的向量称为晶格向量。这个几何位置称为布拉维晶格或空间晶格。

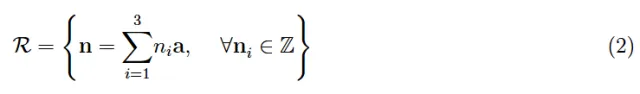
定义2：基本平移向量确定了一个平行六面体，称为原始胞。

 

分配一个晶格并不意味着唯一确定基本平移向量。除了平移对称性外，还可以有关于某些轴的旋转对称性。更准确地说，晶格的一个普通向量n被转化为由相同节点标记的向量n'。对于旋转，相应的对称性被表示为，例如，C6，C9，关于60˚和90˚及其整数倍的旋转。然后我们有反演n → n' = −n，以及关于指定平面的镜像反射。通过添加相同的变换n → n' = n，这样的变换集合具有代数群结构，称为布拉维晶格的对称群。有14个对称群，因此有14个布拉维晶格，进而产生230种晶体结构。

 

维格纳-赛兹单元

 

原始胞可以以几种不同的方式选择。一般来说，这不保留晶格在单个胞级别的对称性。图2展示了一个具有明显六角对称性的二维晶格的例子。通过指定的原始胞选择，我们看到这种对称性在局部没有保留，意味着单位格本身不展示这种对称性。

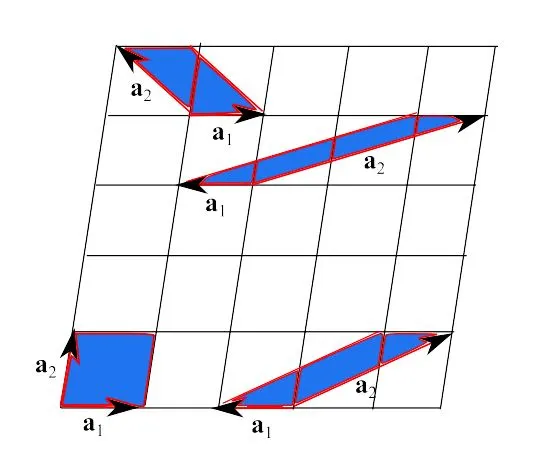
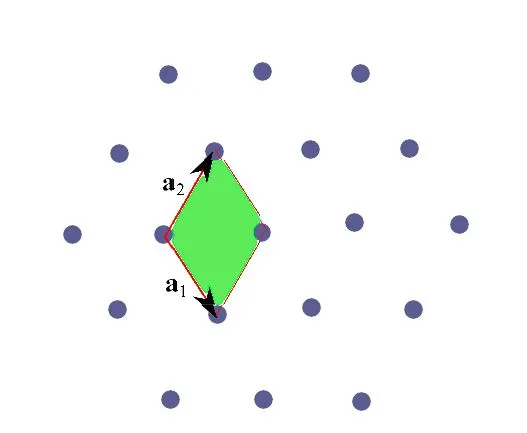
然而，有一种构造与晶格具有相同对称性的原始胞的方法：

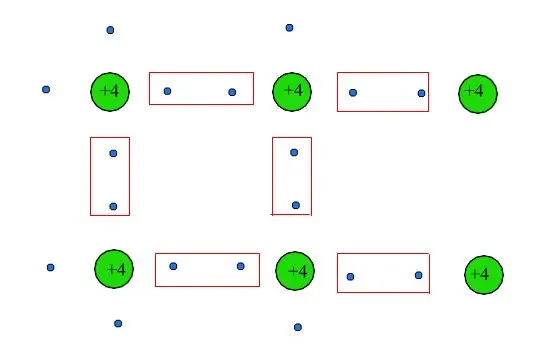
1.从一个指定的节点开始，绘制连接该节点及其邻居的线段。

2.在每个线段上，从中点绘制垂直线。获得的原始胞具有六角对称性。

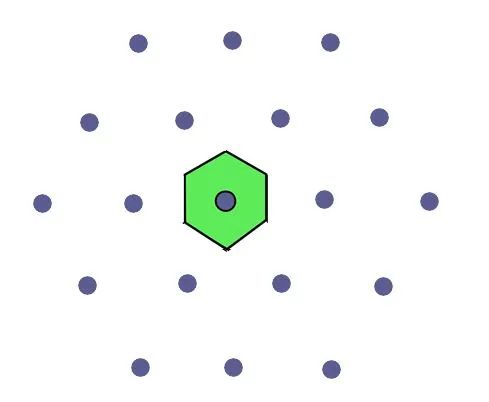
上述程序具有普遍有效性，因此，它在局部级别，即单个原始胞级别，再现了晶格对称性，这称为维格纳-赛兹单元。

 

硅碳化物和氮化镓

 

一般来说，有由基本单元如原子组成的分子或晶体类型的复合系统。以钠原子（Na）和氯原子（Cl）为例。前者的原子序数为Z = 11，而后者为Z = 17。如果我们“靠近”两个原子，钠失去一个电子，变成正离子Na+，丢失的电子被氯获得，氯变成负离子Cl^-。这些离子通过静电性质的力（离子键）相连。结果是形成了一个分子。这种键合没有饱和性，意味着它可以（静电地）传播到其他离子，产生一种特定的凝聚结构，称为离子晶体。

然而，在分子晶体中，凝聚力是由范德瓦耳斯力引起的，这种力作用于诸如H2、O2、CO以及各种碳化合物之间的分子。

共价晶体，硅和锗就是这样的情况：得益于价电子，与邻近原子建立了键。

Si (Z = 14)；Ge (Z = 32)

两者都有四个价电子，与邻近的电子形成键，每对电子都处于自旋单态（即，反平行自旋）。

类似的配置，即共价键的三维映射，也表现在硅碳化物和氮化镓上。硅碳化物在自然中以矿物形式（莫桑石）很少存在，因此通过从碳和硅出发按等比例合成产生，以获得两种化学元素的原子浓度相同。

 

硅碳化物的晶体形态：α-SiC具有六角结构，而β-SiC具有面心立方结构。在文献中，常用H-SiC和C-SiC的符号来区分阿尔法和贝塔状态，即六角和立方对称性。

 

硅碳化物具有有趣的热性能，例如低热膨胀系数和高升华温度。这些特性应用在功率电子器件中可以提供显著可靠性，也是目前汽车电子领域高压电控系统中SiC高采用率的原因。

 

相比之下，氮化镓在自然中以闪锌矿（一种锌和铁的硫化物）的形式存在，在这种分布稀少的情况下，提纯生产极其困难。与SiC相比，氮化镓在射频电子学中表现最佳，因为它具有更高的电子迁移率。我们从GaN和SiC的晶体结构中分析出平，GaN由于其热特性，包括高热导率，使其在环境中更好地散热，而SiC硅碳化物更适用于功率电子学。