定积分-黎曼和的极限解析

定积分如果存在就是一个具体的数值，这个精确的定义是黎曼给出的，所以也叫黎曼积分。

定积分的概念起源于求平面图形的面积和其他的一些实际问题。主要用的思想是微元法（元素法）。

主要的思想就是 分割，取近似值，求和，取极限

定积分的几何意义：其绝对值表示曲线梯形的面积

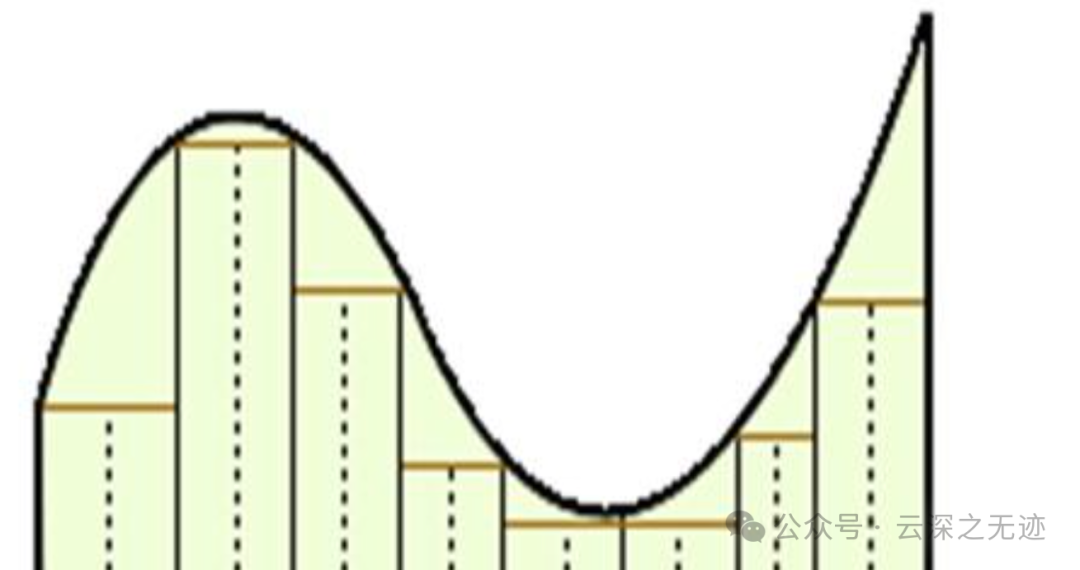
大概就是这样，真丑

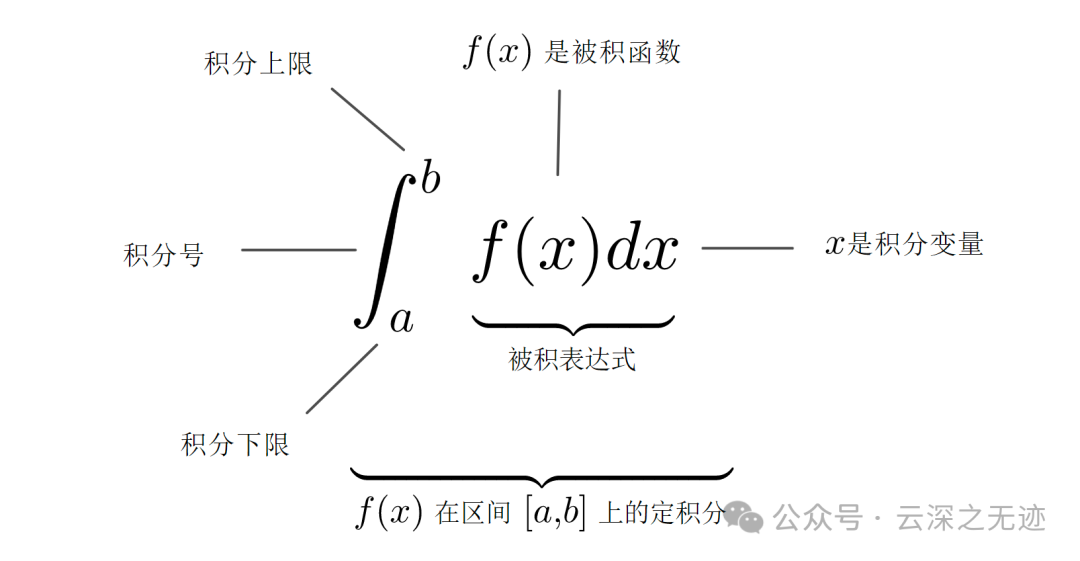
公式是这样的

定积分（外文名：definite integral）是分的一种，是函数f(x)在区间[a,b]上积分和的极限。 

这里应注意定积分与不定积分之间的关系：若定积分存在，则它是一个具体的数值，而不定积分是一个函数表达式，它们仅仅在数学上有一个计算关系（牛顿-莱布尼茨公式）。

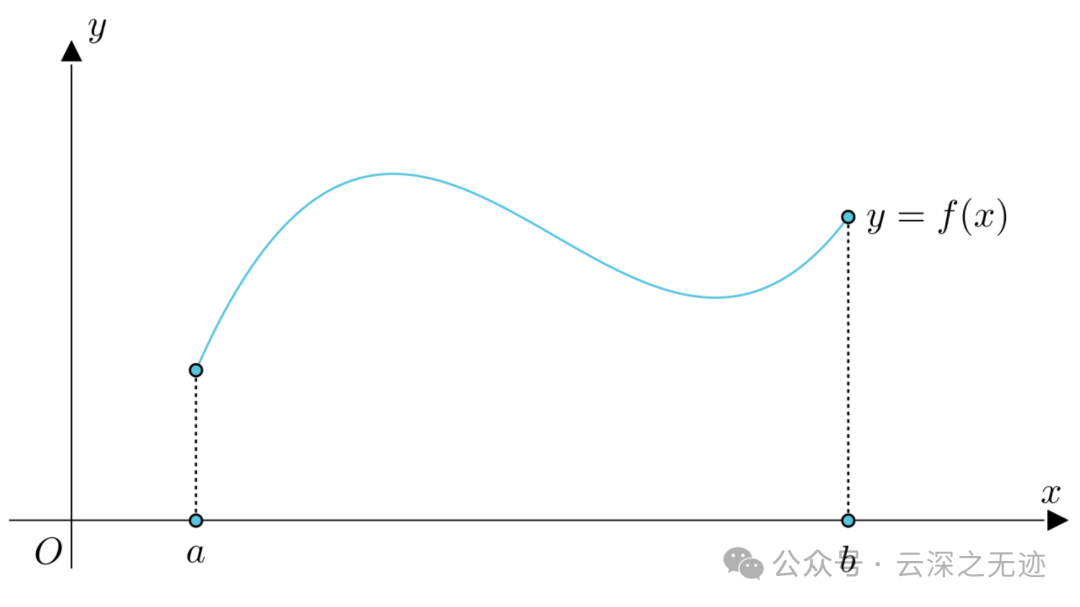
首先是一个有界的函数

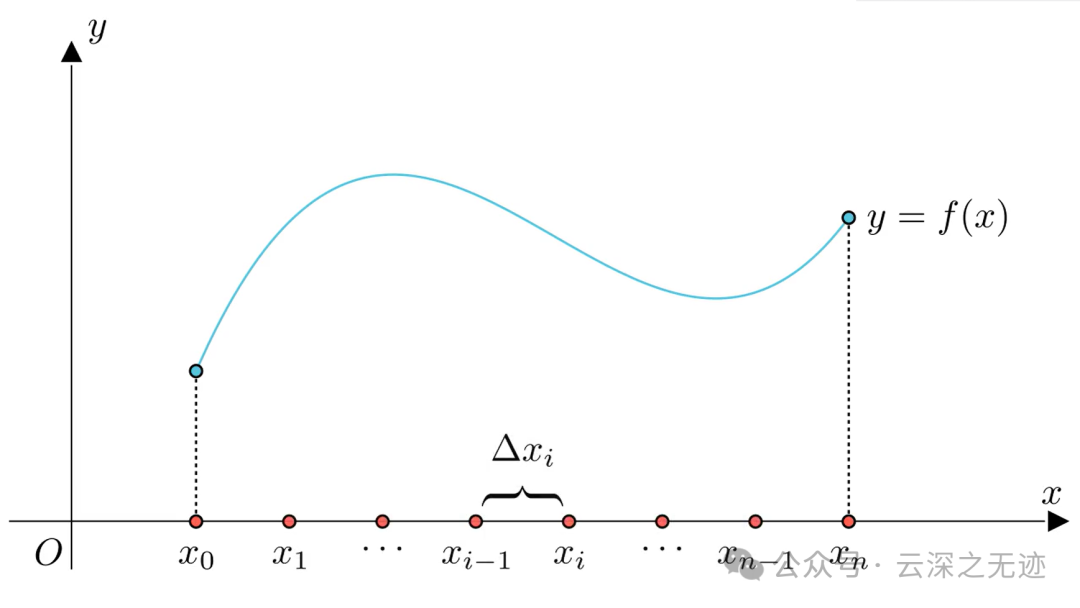
接着在下面切片，一条一条的

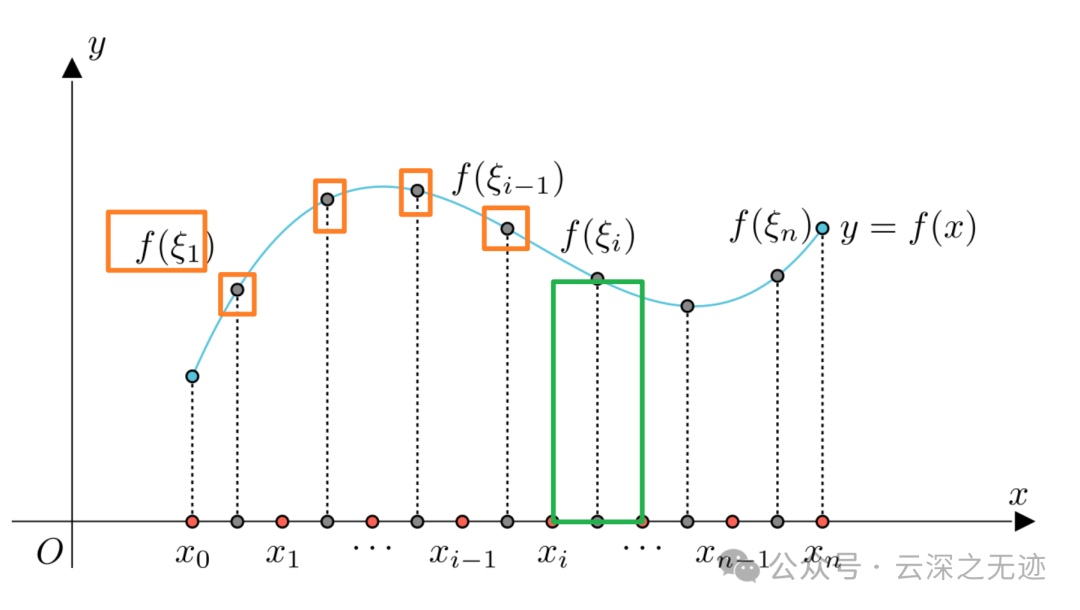
在区间里面任意的找一点，不是中点

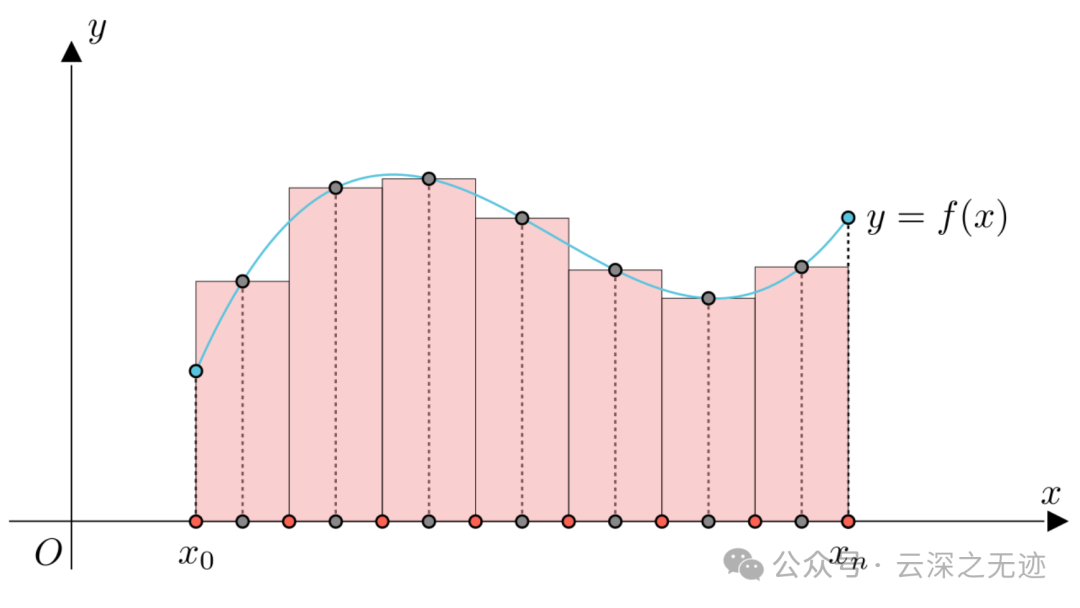
然后就求和呗，一块一块的

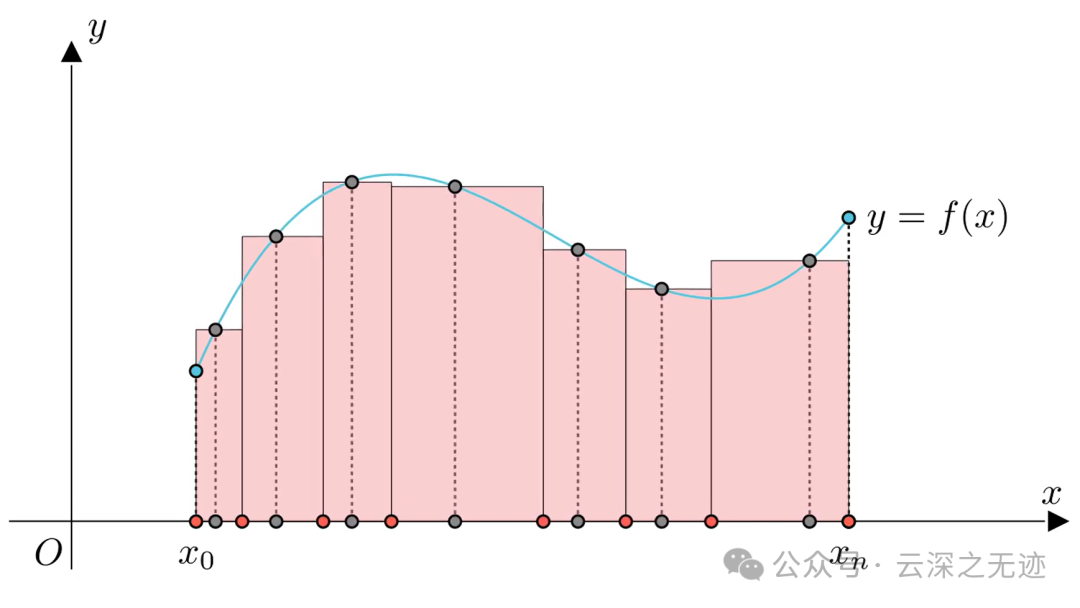
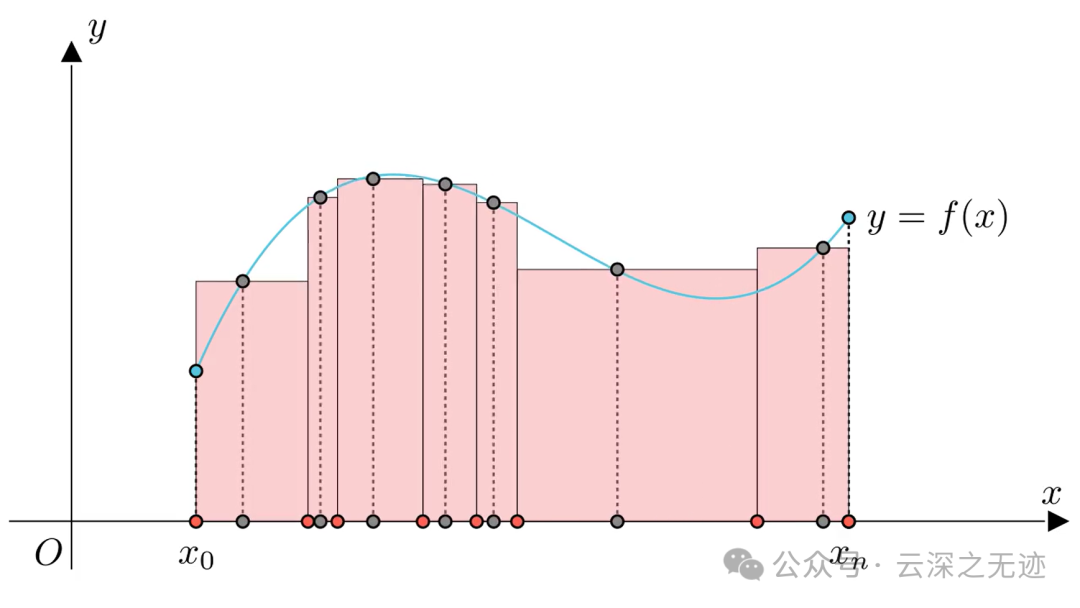
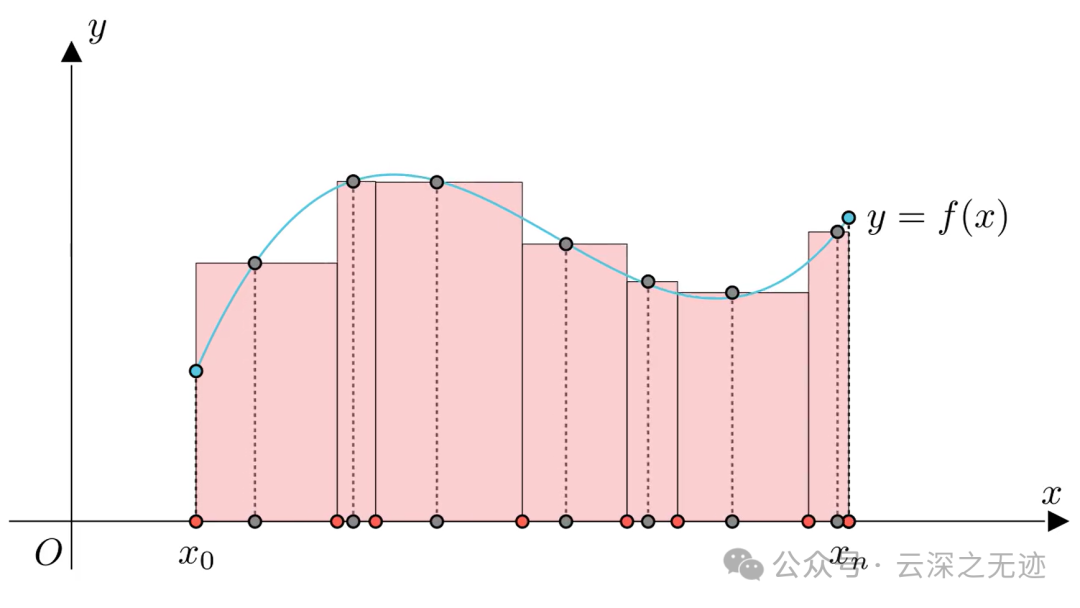
以上三张图非常精彩

说明了小区间的点是任意取的，所以导致这个矩形的面积不是固定的。

这个就是最后一步了，分割完怎么办？

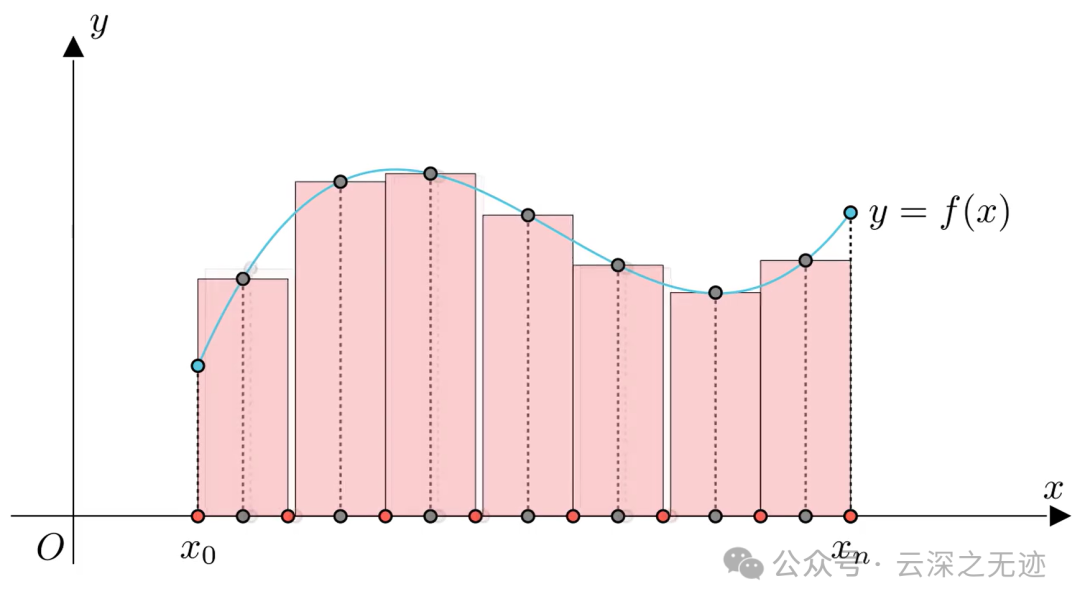
一开始很粗

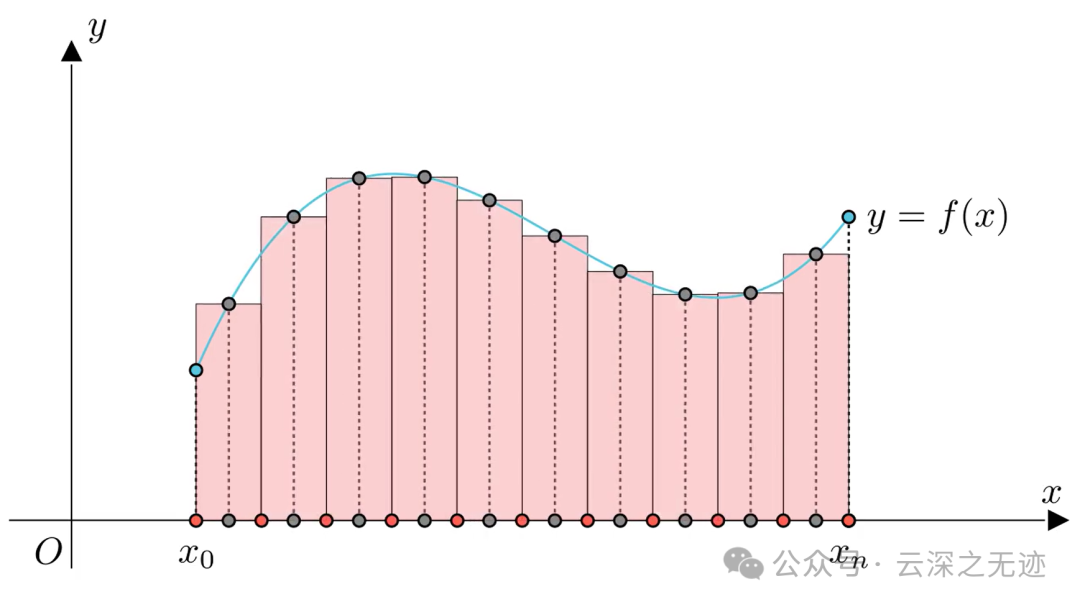
进一步变小

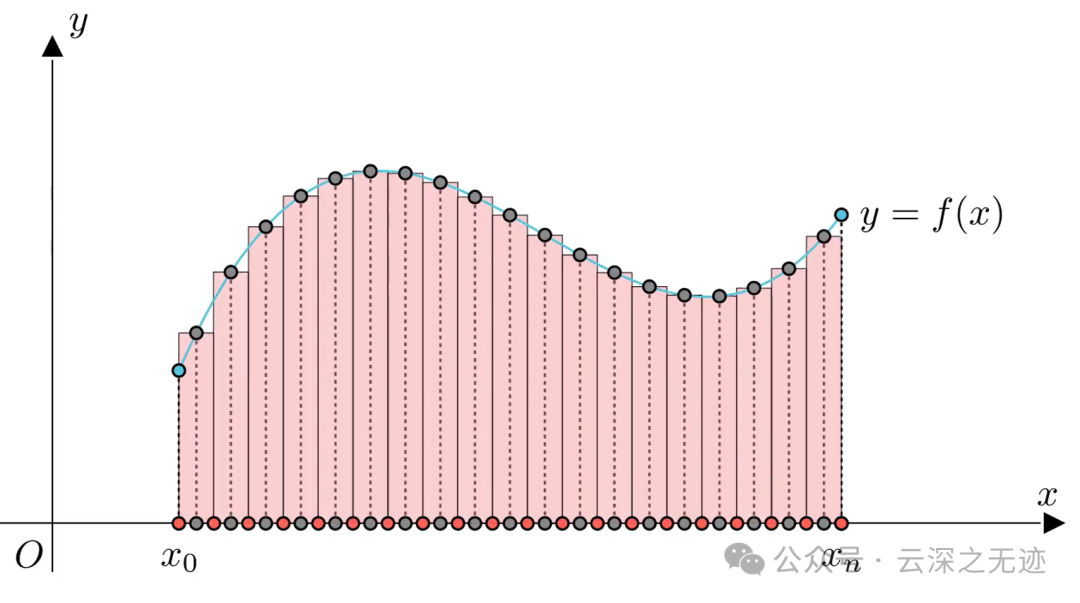
很密集

定积分的求解其实和不定积分的求解方法差不多，只是最后要利用牛顿莱布尼茨公式将上下限代入原函数求差值。

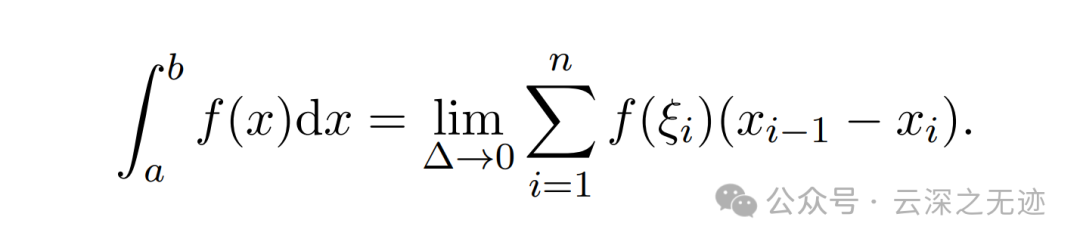
最后再看一眼这个公式

黎曼和的极限是定积分，但是一般只需要Newton-Leibniz公式就可以计算定积分的值而不需要黎曼和。

因此，对于求和式的极限，如果能把它写成黎曼和的形式，那么其极限就是定积分的值。

并不是所有函数都可积，但是连续函数是可积的，记住三类：

1.连续函数

2.单调函数

3.在[a,b]上有界但是有且仅有有限个间断的点或无定义的点函数。

可积函数必须有界，无界函数都不可积。

 

 

审核编辑：刘清