快速掌握运算的4个经典电路分析

运放电路

由运算放大器组成的电路，简称为运放电路。

这些电路可以说是五花八门，是我们学习模拟电子技术的一个重要内容，更是一个电子工程师必须掌握的电路之一。运放电路有多种类型，是不是我们把它们牢牢记住就行了呢?

不是!毕竟电路是会变的，换个套路你如果就不会，这样就没有意义了。正确的打开方式还是应该理解它，消化它。

在分析运放电路工作原理时，首先请忘掉什么同向放大、反向放大，什么加法器、减法器，什么差动输入……暂时忘掉那些输入输出关系的公式……这些只会干扰你，让你更糊涂﹔也请各位暂时不要理会输入偏置电流、共模抑制比、失调电压等电路参数，这是设计者要考虑的事情。我们理解的就是理想放大器，因为理解了理想放大器，多数情况是够用的

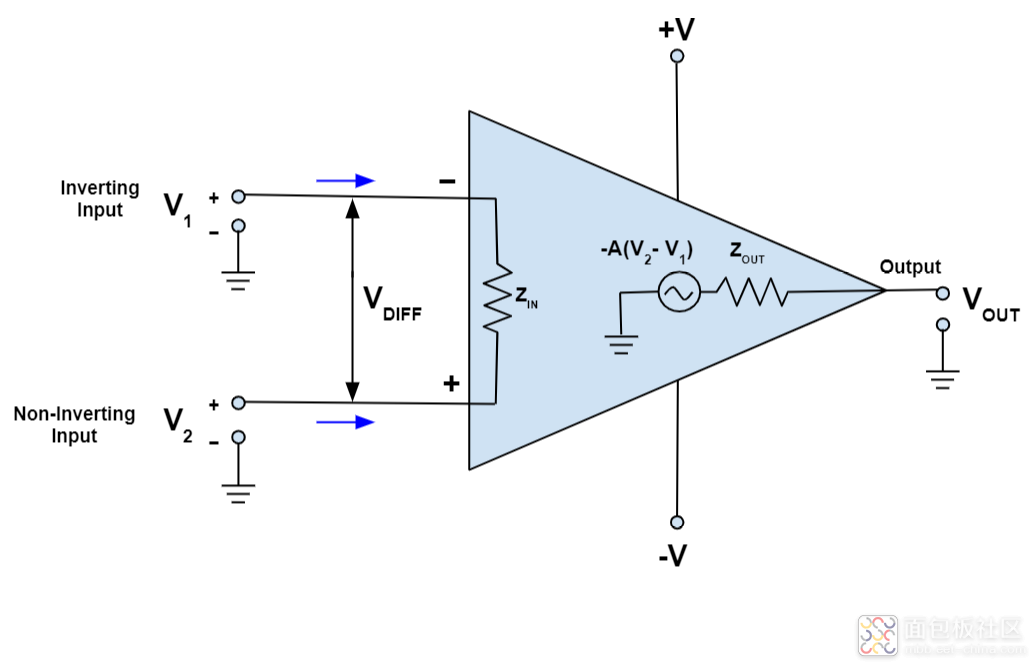
现在，通过两招就能解决大部分运放问题，并且，这两招在所有运放电路的教材里都写得明白，就是“虚短”和“虚断”，不过要把它运用得出神入化，就要有较深厚的功底了。

基于这一理论，我们通过4个经典电路，来快速掌握运算的分析方法!

关于虚短和虚断

由于运放的电压放大倍数很大，一般通用型运算放大器的开环电压放大倍数都在 80dB 以上。而运放的输出电压是有限的，一般在 10 V～14 V。因此运放的差模输入电压不足 1 mV，两输入端近似等电位，相当于 “短路”。开环电压放大倍数越大，两输入端的电位越接近相等。我们用这样的反推来理解虚短的概念。

“虚短”是指在分析运算放大器处于线性状态时，可把两输入端视为等电位，这一特性称为虚假短路，简称虚短。显然不能将两输入端真正短路。(输入差模电压不大于1mv)

如何理解“虚断”呢?由于运放的差模输入电阻很大，一般通用型运算放大器的输入电阻都在 1MΩ以上。因此流入运放输入端的电流往往不足 1uA，远小于输入端外电路的电流。故通常可把运放的两输入端视为开路，且输入电阻越大，两输入端越接近开路。

“虚断”是指在分析运放处于线性状态时，可以把两输入端视为等效开路，这一特性 称为虚假开路，简称虚断。显然不能将两输入端真正断路。(差模输入电阻无穷大)

好了，概念就介绍到这里，我们来用以上的理论，来分析几个案例，看是否好使?

第一个案例：

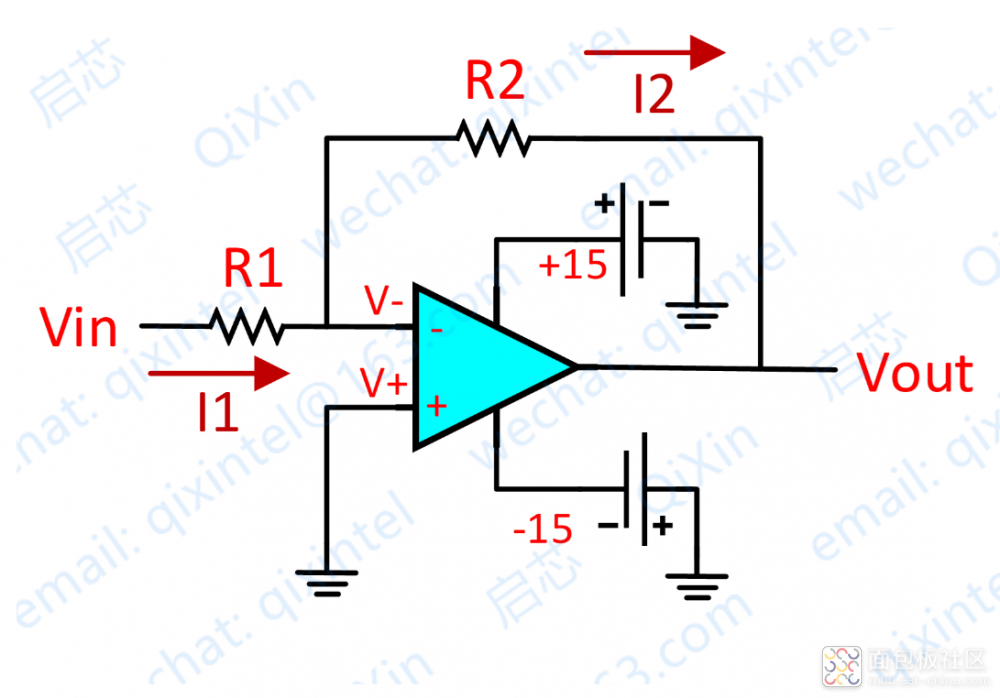
由上图，分析如下：

首先，根据虚短，图一运放的同向端接地=0V，反向端和同向端 虚短，所以也是 0V

其次，根据虚断，反向输入端输入电阻很高，虚断，几乎没有电流注入和流出

那么R1和R2相当于是串联的，流过一个串联电路中的每一只组件的电流是相同的，即流过 R1 的电流和流过 R2 的电流是相同的。

流过 R1 的电流 I1 = (Vi - V-)/R1

流过 R2 的电流 I2 = (V- - Vout)/R2

V- = V+ = 0

I1 = I2

求解上面的代数方程

Vout = (-R2/R1)*Vi

这样，我们就设计了一个最经典的反向比例放大器

第二个案例：

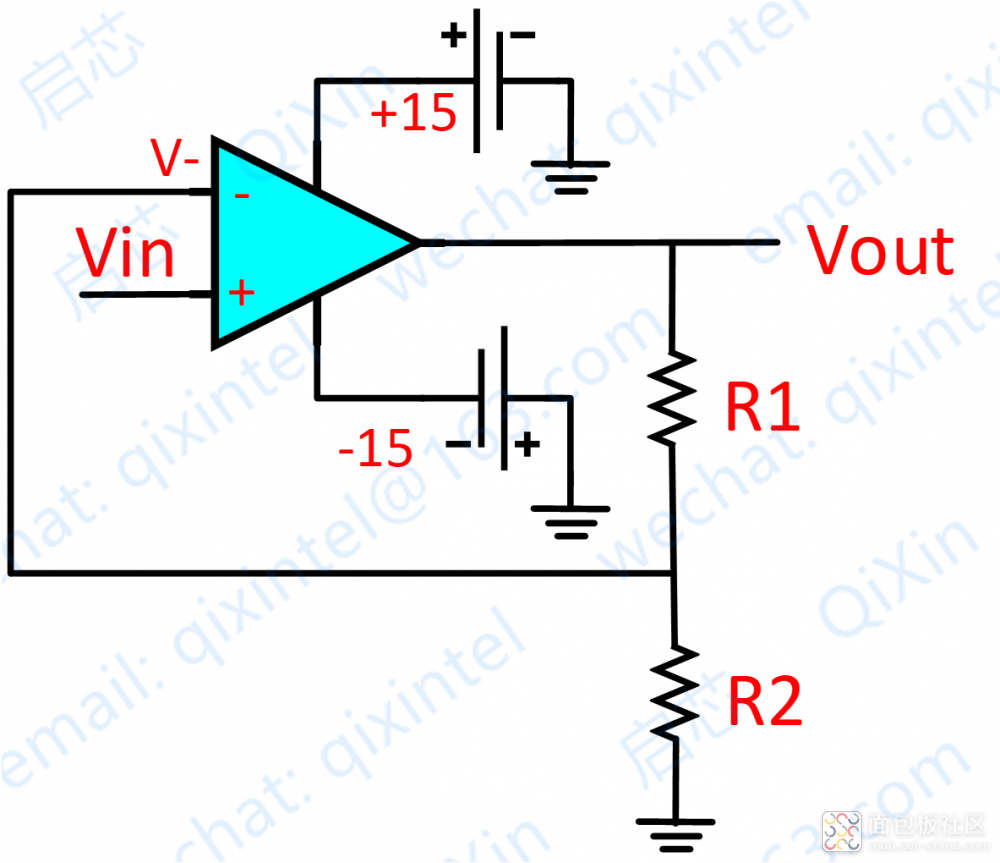
再看上图，分析如下：

Vi 与 V- 虚短，则 Vi = V-

因为虚断，反向输入端没有电流输入输出，通过 R1 和 R2 的电流相等，设此电流为 I

由欧姆定律得：I = Vout/(R1+R2)

Vi 等于 R2 上的分压， 即：Vi = I*R2

由上面式子得

Vout=Vi*(R1+R2)/R2

这样，我们就设计了一个同向放大器。

第三个案例：

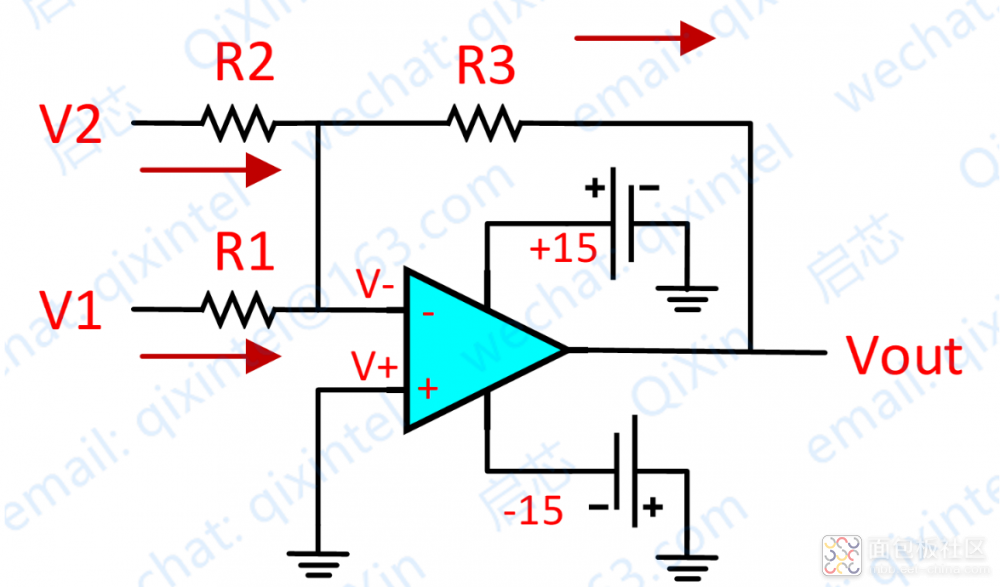
再看上图，分析如下：

由虚短知：V- = V+ = 0

由虚断及基尔霍夫定律知，通过 R2 与 R1 的电流之和等于通过 R3 的电流，故 (V1 – V-)/R1 + (V2 – V-)/R2 = (Vout – V-)/R3

联立上面两个式子很容易得到 V1/R1 + V2/R2 = Vout/R3

如果存在 R1=R2=R3，则上式变为 Vout=-(V1+V2)，

这样，我们就设计了一个加法器啦。

我一直都认为，实践是学习的硬件电路知识最好的方法。但是，动手搭建电路很费时间，而设计原理图打PCB板不仅花时间而且费钱，因此，折衷最好的方法就是仿真了。平心而论，只要模型准确，实际上，仿真的结果是无限接近实际情况的。

况且，通常我们只是工程上设计，判断趋势，知道大体方向与数值即可。并不需要太严谨的结果，因此，从这个方面来说，仿真大多数情况下，用来分析问题，是完全够用的。

对于上面这个案例，我们仿真看看，先看简单的，这个电路和上面的电路唯一不同的是加了平衡电阻

下面是R1=R2=R4的情况，可以看到结果是符合我们预期的，即VO=V1+V2，仿真图例如下

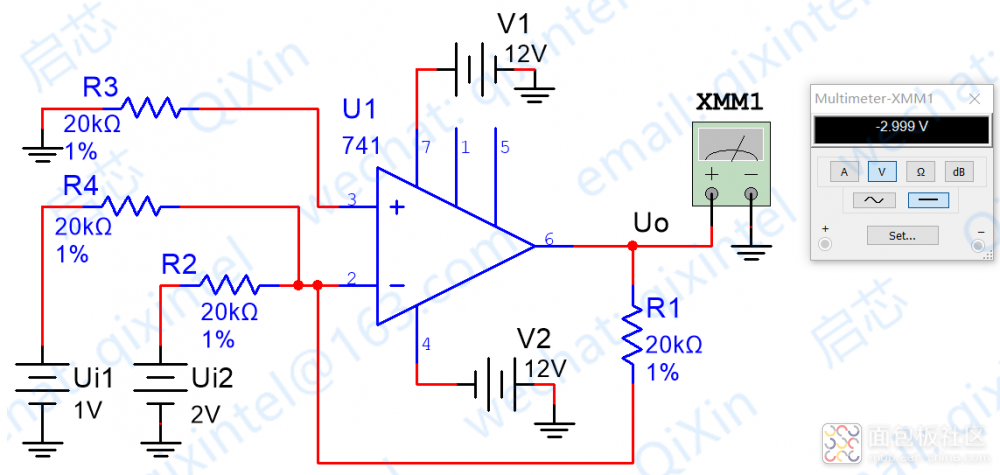
下面是R2=R4 R1=3*R2的情况，可以看到结果也是符合我们预期的，即VO=3*(V1+V2)，仿真图例如下

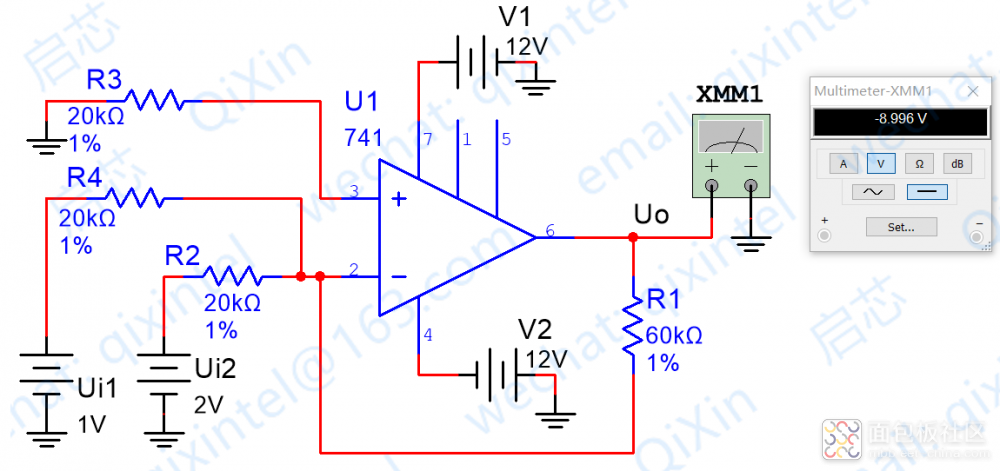
这个电路实际的应用电路，比如用OP07C搭建的低频噪声放大电路，如下图

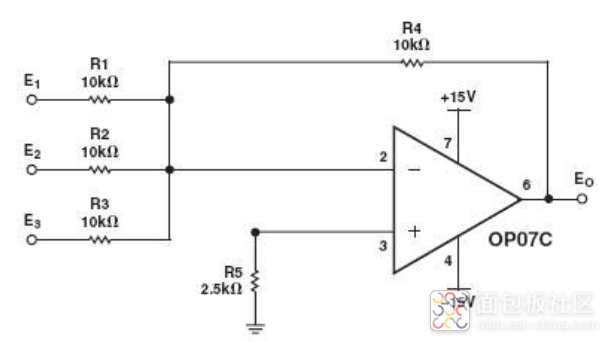
这个电路，比上面讲过的电路稍微复杂，但基本的分析原理是一样的。大家，可以试着计算一下输出公式。

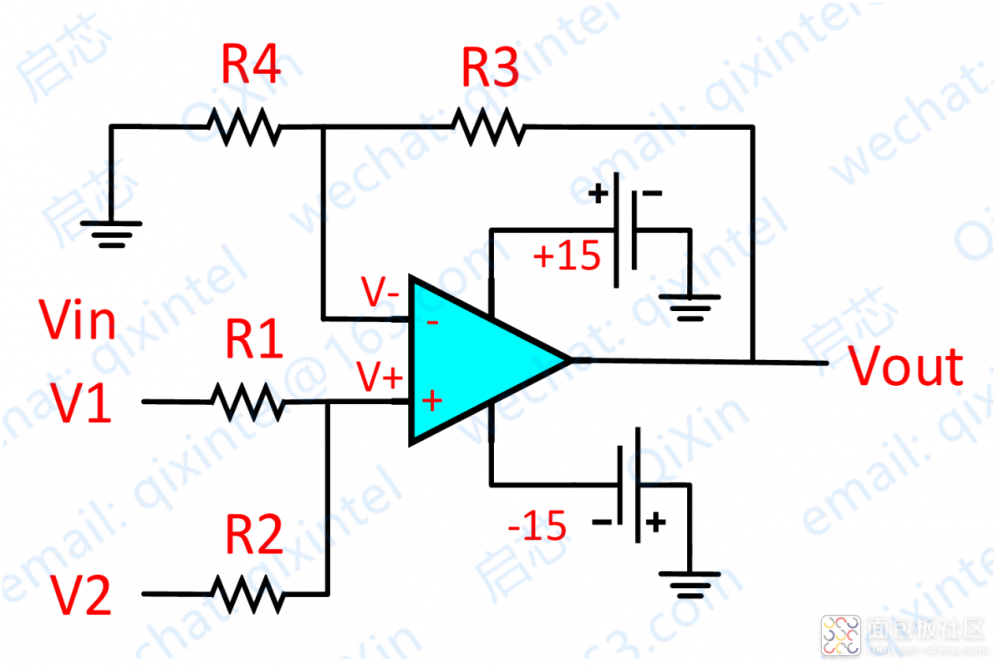
再看上图，分析如下：

因为虚断，运放同向端没有电流流过，则流过 R1 和 R2 的电流相等，同理流过R4和R3的电流也相等。

所以，很容易推出，(V1–V+)/R1 = (V+ - V2)/R2

(Vout – V-)/R3 = V-/R4 ……b

然后，再由虚短知：V+ = V-

如果 存在条件R1=R2，R3=R4，

则由以上式子可以推导出 V+ = (V1 + V2)/2

V- = Vout/2

故 Vout = V1 + V2

这样，我们就设计了一个新的加法器。

由上面四个例子，我们可以看到基本的运算放大器电路，无论电路的形式、连接如何变化，但只要掌握了基本的原理，虚短和虚断，运放的电路基本都可以迎刃而解!

 

 

 

 

审核编辑：黄飞