为什么格雷码可以辅助解决多bit跨时钟域的问题​？求解

为什么格雷码可以辅助解决多bit跨时钟域的问题？读完这篇文章，你就会进一步了解事情的本质。

        重要的事情讲三遍，由前文可知：

        单bit通过两级同步打拍可以有效的解决亚稳态问题。

        单bit通过两级同步打拍可以有效的解决亚稳态问题。

        单bit通过两级同步打拍可以有效的解决亚稳态问题。

        格雷码是一种反射二进制码编码方式，它两个连续的值只相差一位(二进制数字)。它属于一种被称为最小变化码的代码，在这种代码中，相邻的两个码字中只有一个比特发生变化。这是一个未加权的代码，这意味着没有为位置分配特定的权重。

        生成方式如下图所示

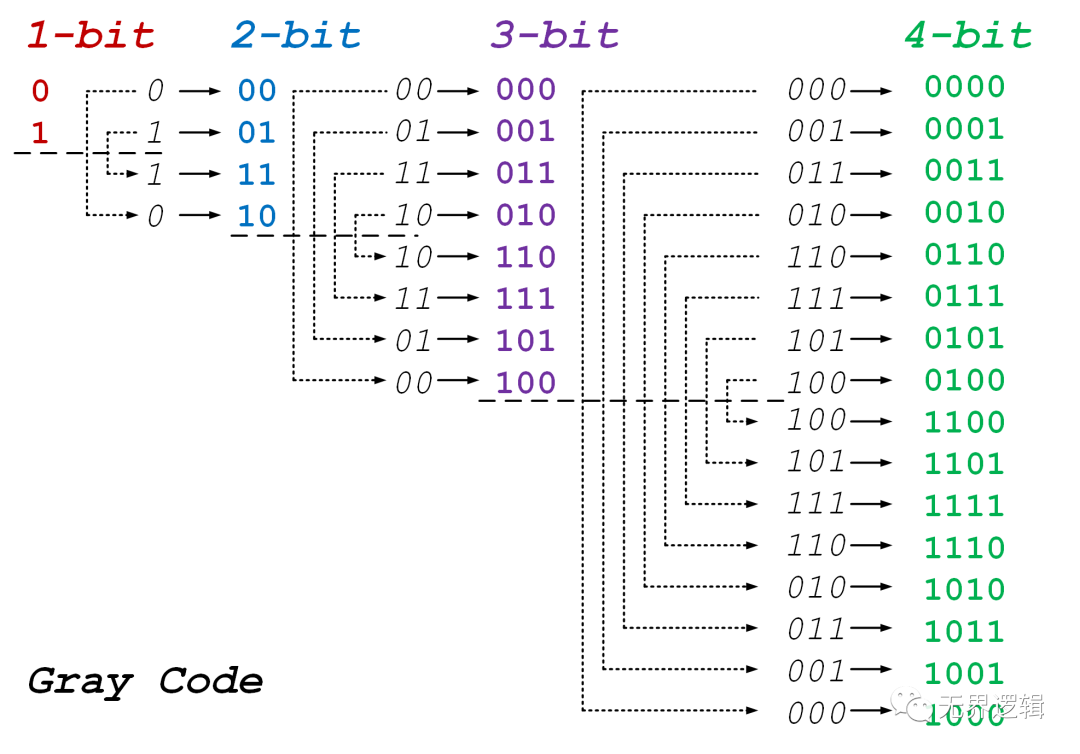
        4位宽格雷码与十进制二进制的对应关系如下：

Decimal	Binary	Gray
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

        如4bit的格雷码一头一尾也是两个相邻码，一个是0000，一个是1000，它们的变换也是只有1bit。是不是很熟悉。对头，“如果是单bit变化的话，可以采用两级打拍的方式进行时钟域同步”。

        按照这个思路，我们是不是可以将多bit数据转换为格雷码？然后采用两级打拍的方式同步呢？如果源数据是递增的方式，可以考虑这种处理方式的可能性。如果源数据也是变化无常的，则这种思路就只能嘎然而止了。

二进制转格雷码的方法：

        Gray Code最高位G[N]等于二进制码最高位B[N]，Gray Code第n位等于二进制码B[n+1]位异或二进制码B[n]位。

以4位宽码字为例，RTL图如下：

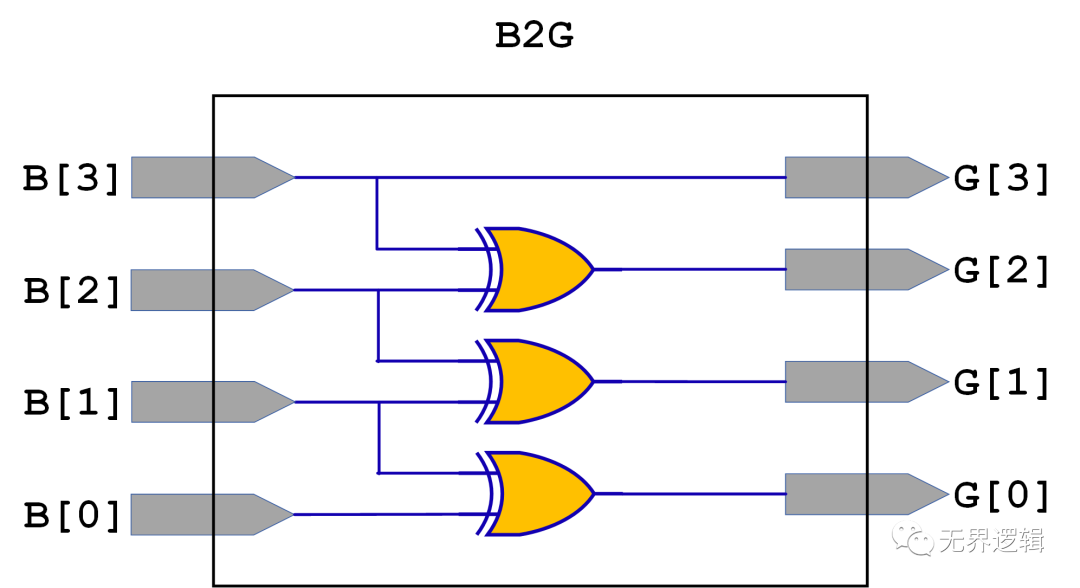
格雷码转二进制码的方法：

        二进制码最高位B[N]等于格雷码最高位G[N]，二进制码第n位B[n]等于二进制码B[n+1]位异或格雷码第n位G[n]。

以4位宽码字为例，RTL图如下：

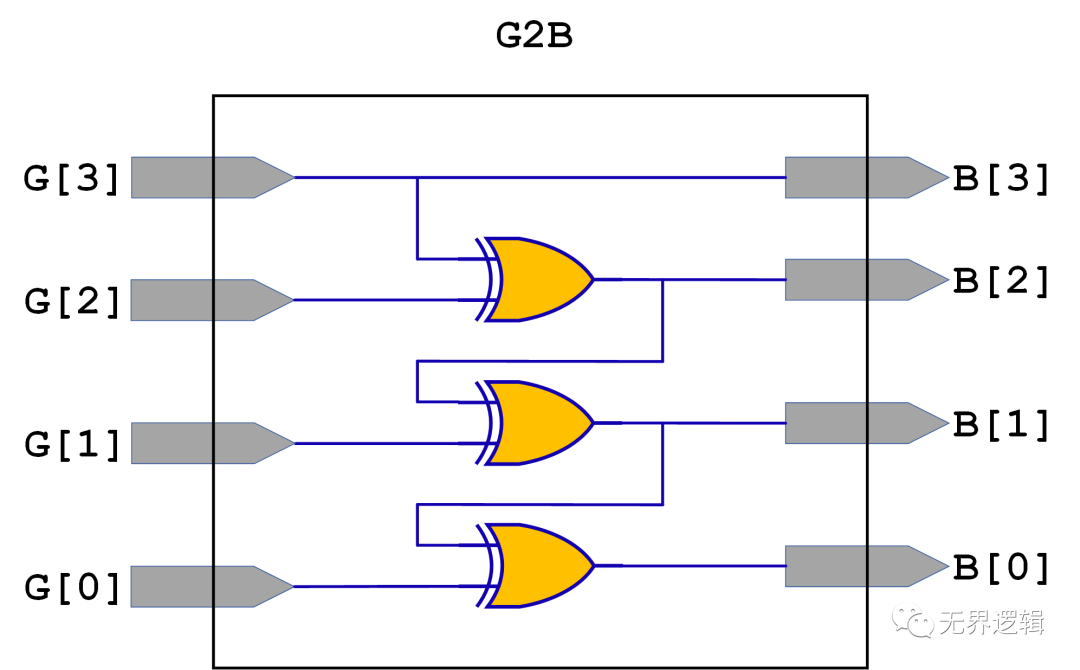
        那么，异步FIFO是如何通过格雷码，实现跨时钟域高效处理的呢？我们下期再讲。

        你是否有所收获？你肯定可以参考上述原理和电路，写出二进制与格雷码之间的verilog转换代码。

 

module B2G #(
   parameter N = 4
(
input    [N-1:0]  B,
output  reg  [N-1:0]  G
);


integer i;
always @(*) begin
  G[N-1]  = B[N-1];
  for(i=N-2; i>=0; i=i-1) begin
    G[i] = B[i+1] ^ B[i];
  end
end


endmodule

 

 

module G2B #(
   parameter N = 4
(
input    [N-1:0]  G,
output  reg  [N-1:0]  B
);


integer i;
always @(*) begin
  B[N-1]  = G[N-1];
  for(i=N-2; i>=0; i=i-1) begin
    B[i] = B[i+1] ^ G[i];
  end
end


endmodule

 

审核编辑：刘清