时间序列分析的异常检测综述

时间序列分析是一种非常实用且强大的技术，用于研究随时间变化的数据，例如销售、交通、气候等。异常检测是识别偏离数据正常趋势的值或事件的过程。在本文中，我将解释什么是时间序列，它的组成部分是什么，它与其他类型的数据有何不同，如何检测时间序列中的异常，以及进行此类检测的最常见技术。

时间序列分析简介

时间序列是在不同时点记录一个或多个变量值的数据。例如，每天访问网站的人数、每月城市的 average 温度、每小时的股票价格等。时间序列非常重要，因为它们允许我们分析过去，理解现在，并预测未来。此外，时间序列帮助我们发现数据中的隐藏模式和趋势，这些可以用于改进决策和策略。

然而，时间序列分析也带来了挑战，并且与非时间数据分析有所不同。主要区别之一是时间序列是时间依赖的，即数据的排序和范围是相关且不能被忽视或更改的。另一个区别是时间序列通常是非平稳的，即它们的统计属性（如均值和方差）会随时间变化。这使得应用传统的统计方法变得困难，这些方法假设数据的平稳性。

此外，时间序列分析需要对异常检测采取不同的方法。异常是显著偏离数据正常趋势的值或事件。异常可能是由测量错误、结构变化、欺诈活动、特殊事件等引起的。异常检测很重要，因为它可以提供隐藏在数据中的问题或机会的宝贵见解。然而，检测时间序列中的异常比非时间数据更复杂，因为必须考虑到数据的时序依赖性、非平稳性和动态性质。

时间序列分析的基本概念

在我们详细讨论时间序列分析和异常检测技术之前，我们需要定义什么是时间序列及其组成部分。时间序列是在不同时点测量的一个或多个变量值的序列。

时间序列有三个主要组成部分：日期、时间和特征。日期和时间指示了何时测量变量值。特征是我们希望分析的变量。在我们的示例中，日期是月份的一天，天气是星期几，特征是访客数量。

为了能够分析时间序列，我们需要满足某些要求。第一个要求是有足够的数据点，即随时间变化的变量观测值。所需的数据点数量取决于我们想要进行的分析类型以及数据收集的频率。例如，如果我们想要分析数据的季节性，即数据作为时间的函数的周期性变化，我们需要至少一个完整的观测周期，涵盖所有可能的季节。如果数据每天收集一次，我们需要至少一年的数据才能分析年度季节性。

第二个要求是对数据的领域有深入的了解，即数据生成的背景和变量的含义。这有助于我们解释分析结果并识别异常的可能原因。例如，如果我们分析网站的访客数量，我们需要知道网站的类型、目标受众、目标、影响流量的因素等。

第三个要求是对分析目标有清晰的定义，即我们想要从数据中发现什么以及我们想要如何使用它。分析的目标可能因用例和研究问题而异。例如，我们可能想要分析时间序列有：

描述数据随时间的行为及其主要特征

基于过去的值预测未来的数据值

检测数据中的异常及其原因

测试关于数据及其关系的假设

优化数据驱动的决策和行动

理解时间序列中的异常

在我们查看如何检测时间序列中的异常之前，我们需要了解异常是什么以及它们如何在数据中表现出来。异常是显著偏离数据正常趋势的值或事件。异常可以分为两种类型：点状或集体。点状异常是与时间序列中的其他值非常不同的孤立值。集体异常是与时间序列的其他部分不同的一组值。

例如，在下面的图中，我们可以看到一个月内每天记录网站访客数量的时间序列。点状异常用红色标出，集体异常用蓝色标出。

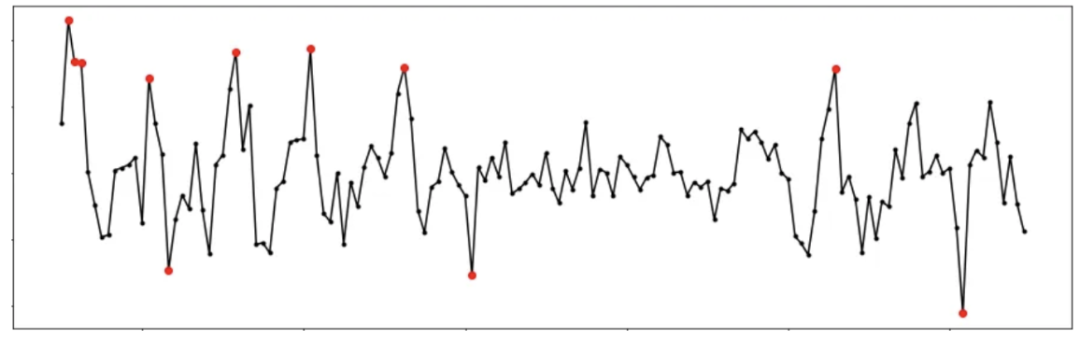
异常可能有不同的原因和含义。一些异常可能是由于测量、传输或数据处理错误引起的。这些异常通常被称为噪声，可以被忽略或纠正。其他异常可能是由于结构性变化、欺诈活动、特殊事件或其他影响数据的因素引起的。这些异常通常被称为信号，检测和分析它们可能很重要。

为了检测时间序列中的异常，我们首先需要对数据随时间的正常运动有所期望。这些期望是基于对时间序列的主要组成部分的分析，这些组成部分是：

趋势，即数据长期变化的方向和速度。例如，上升趋势表明数据随时间增加，而下降趋势表明数据随时间减少。

季节性，即数据作为时间的函数的周期性变化。例如，年度季节性表明数据具有每年重复一次的循环模式，例如玩具店的销售在12月增加而在1月减少。

周期性，即数据作为时间的函数的不规则变化。例如，经济周期性表明数据具有依赖于外部因素（如GDP、通货膨胀、失业率等）的波动趋势。

噪声，即数据作为时间的函数的随机变化。例如，噪声可能是由测量、传输或处理错误引起的。

在下面的图中，我们可以看到一个具有上升趋势、年度季节性和噪声的时间序列示例。

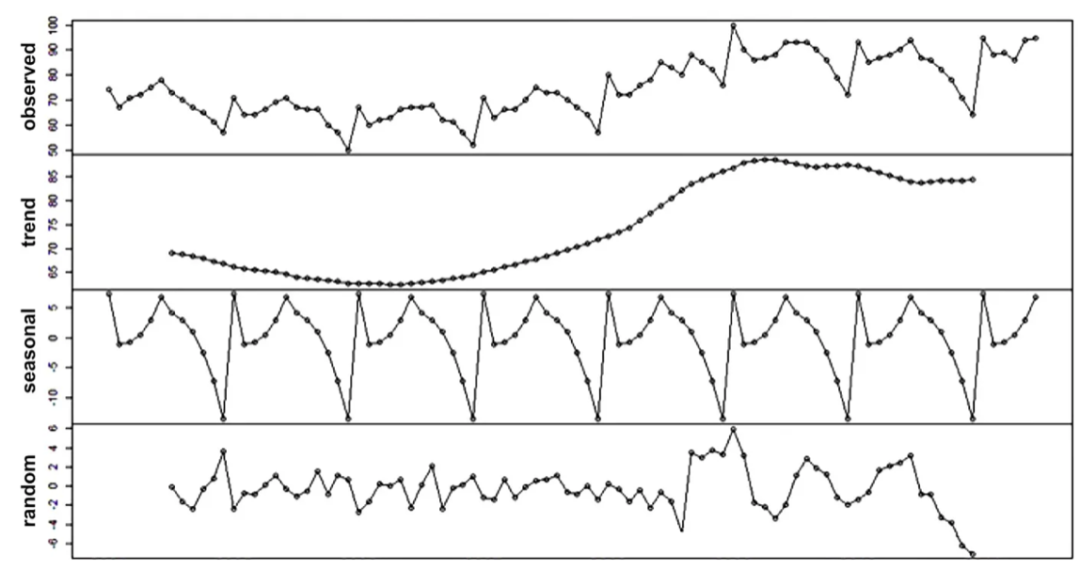
当分析时间序列时，我们需要考虑这些组件并了解它们如何随时间变化。一个或多个组件的变化可能会引起异常。因此，通过理解和建模时间序列的趋势、季节性、周期性和噪声，我们可以建立对正常行为的期望，并相应地检测偏离这些期望的异常。

时间序列分析的数据要求

如我们所见，为了能够分析时间序列并检测异常值，我们需要拥有满足特定要求的数据。第一个要求是拥有足够数量的数据点，即随时间变化的变量观测值。所需的数据点数量取决于我们想要进行的分析类型以及数据的收集频率。例如，如果我们想要分析数据的趋势，我们需要至少有十二个覆盖相当长时间范围的数据点。如果我们想要分析数据的季节性，我们需要至少有一个完整的观测周期，涵盖所有可能的季节。如果我们想要分析数据噪声，我们需要至少有二十个足够变化的数据点。

第二个要求是拥有捕捉时间变化的数据，即反映变量随时间变化的变动。这意味着数据应该在规律且一致的时间间隔内收集，不跳过或重复某些观测值。此外，数据必须是时间对齐的，即每个观测值必须对应于变量被测量的时间。这暗示着数据必须转换为适合时间序列分析的格式，例如日期时间格式。

第三个要求是拥有满足时间序列主要组件（即趋势、季节性和噪声）分析的最低要求的数据。这些要求根据我们想要用于分析的模型而有所不同。例如，如果我们想要使用线性模型来分析趋势，我们需要拥有在变量和时间之间具有线性关系的数据。如果我们想要使用指数模型来分析趋势，我们需要拥有在变量和时间之间具有指数关系的数据。如果我们想要使用ARIMA模型来分析季节性和噪声，我们需要拥有稳定或可微分的数据。

时间序列分析中的差分

如我们所见，时间序列分析中的一个主要挑战是数据中存在非稳定性，即数据的统计属性（如均值和方差）随时间变化。这使得应用传统的统计方法变得困难，因为这些方法假设数据是稳定的。为了使用这些方法，我们必须首先转换数据，使其变得稳定，或至少近似稳定。进行这种转换的最常见技术之一是差分。

差分包括从时间序列中的每个值中减去前一个值，从而得到一个代表数据随时间变化的新的时序。例如，如果我们有一个时间序列 {x1, x2, x3, …}，它的一阶差分是 {x2 - x1, x3 - x2, …}。差分可以重复多次，从而实现二阶差分、三阶差分等。差分的目的是从时间序列中移除趋势和季节性成分，这些是非稳定性的主要原因。实际上，如果数据具有趋势或季节性，其值将与前一个或后一个值相关。减去这些值可以减少或消除这种相关性。

例如，我们可以看到一个具有上升趋势和年度季节性的时间序列。其一阶差分去除了趋势，但没有去除季节性。其二阶差分去除了趋势和季节性。

差分是最广泛使用的时间序列分析和异常检测模型之一——ARIMA模型的基础。

ARIMA模型介绍

ARIMA模型是时间序列分析和异常检测中广泛使用的模型之一。ARIMA代表自回归差分移动平均模型（Autoregressive Integrated Moving Average）。这个模型结合了三个主要组成部分：

自回归（AR）部分，它建模时间序列值与之前值之间的相关性。例如，如果数据是周期性的，时间序列值将受到过去值的影响。

差分（I）部分，它通过使时间序列差分来建模，使其变得稳定。例如，如果数据具有趋势或季节性，差分将从时间序列中移除这些成分。

移动平均（MA）部分，它建模时间序列误差与之前误差之间的相关性。例如，如果数据有噪声，时间序列误差将受到过去误差的影响。

ARIMA模型有三个主要参数：p、d和q。p参数表示模型中使用的自回归项的数量。d参数表示为了使时间序列稳定而必须对时间序列进行差分的次数。q参数表示模型中使用的移动平均项的数量。例如，ARIMA(1,1,1)模型使用一个自回归项、一个差分和一个移动平均项。

ARIMA模型可以用来描述、预测和检测时间序列中的异常。为此，我们需要遵循几个步骤：

首先，我们需要检查时间序列是否稳定。我们可以使用统计测试，如增强的Dickey-Fuller测试，来检查时间序列的均值和方差是否随时间恒定。

其次，我们需要对时间序列进行差分，直到它变得稳定。我们可以使用图表，如自相关函数图和偏自相关函数图，来确定所需的差分次数。

第三，我们需要使用优化方法，如最大似然法，来估计ARIMA模型的参数。我们可以使用模型选择标准，如赤池信息准则或贝叶斯信息准则，来选择p、d和q参数的最优值。

第四，我们需要使用验证方法，如Ljung-Box测试或Jarque-Bera测试，来验证ARIMA模型。我们可以使用图表，如残差图或预测图，来检查模型是否与数据拟合良好，以及数据中是否存在任何异常。

第五，我们需要使用ARIMA模型来描述时间序列的主要特征，预测未来的时间序列值，并检测时间序列中的异常。我们可以使用准确性度量，如均方误差或平均绝对误差，来评估预测和异常的质量。

时间序列异常检测

在估计和验证我们的时间序列的ARIMA模型后，我们可以使用它来检测数据中的异常。异常是与数据的正常运行趋势显著偏离的值或事件。为了检测异常，我们需要将观察到的时间序列值与ARIMA模型预测的值进行比较。如果两个值之间的差异大于某个阈值，我们可以将观察到的值视为异常。

定义异常的阈值取决于多个因素，如置信水平、误差分布、数据的频繁程度等。通常，我们可以使用置信区间的概念来确定阈值。置信区间是一个以一定概率包含预测值的区间。例如，95%的置信区间意味着预测值在该范围内的概率为95%。如果观察到的值在置信区间之外，我们可以将其视为异常。

当我们在时间序列中检测到异常时，我们还必须尝试理解它们的原因和含义。一些异常可能是由于测量、传输或数据处理错误造成的。这些异常通常被称为噪声，可以被忽略或纠正。其他异常可能是由于结构性变化、欺诈活动、特殊事件或其他影响数据的因素造成的。这些异常通常被称为信号，检测和分析它们可能很重要。

为了理解异常的原因和含义，我们需要使用我们对数据领域的知识，即数据生成的背景和变量的含义。此外，我们需要使用其他信息来源，如其他相关时间序列、历史数据、新闻、报告等。这有助于我们解释异常检测结果并确定可能采取的行动。

在本文中，我们已经看到了如何使用ARIMA模型进行时间序列分析和异常检测。

结论

在本文中，我们已经看到了如何使用ARIMA模型进行时间序列分析和异常检测。我们已经了解了什么是时间序列，它的组成部分是什么，它与其他类型的数据有何不同，如何在时间序列中检测异常，以及进行这些操作的最常见技术。我们已经看到了如何验证数据的平稳性，如何对时间序列进行差分，如何估计和验证ARIMA模型，如何使用ARIMA模型来描述、预测和检测时间序列中的异常，以及如何解释异常检测结果。

时间序列分析和异常检测是研究随时间变化的数据（如销售、交通、气候等）的非常有用的强大技术。这些技术允许我们分析过去，理解现在，并预测未来。此外，这些技术帮助我们发现数据中隐藏的模式和趋势，这可以用来改进决策和策略。最后，这些技术帮助我们识别数据中的隐藏问题或机会，这可能是由数据中的异常引起的。

审核编辑：黄飞