关于极限语言ε-δ的一点理解

好多人都是因为这个地方放弃数学的对吧？

我觉得也不用说什么这个语言是怎么出来的，直接讲我的理解。

“无限接近于X”这个表述方式无法被准确定义。你不能用一个未被定义的词来作为定义本身的一部分。就好像我们写程序一样，一定要保证一开始运行的状态你是可控的。

所以这个ε-δ的工作就是来精确的说明和一个数字无限贴贴的时候应该如何理性的定义。（把原来不确定的动态的靠近过程，转换成了静态的，确定的数）

其实本质是使用了差值，或是叫可以接受的误差。

这里面说了数列和极限：

数列说的是下标，函数说的领域，因为我们研究的一点处的情况。

其实ε 是"error"(误差)、δ 是"distance"(距离)的首字母。实际上，是柯西在他的著作中用ε来表示"error"的。

这个也挺抽象的

目前教科书上面的定义都是这个

wiki百科是这样的，其实是一样的

emmmm，原因是因为采用了‘任意-存在’这种逻辑结构，就读不懂了。

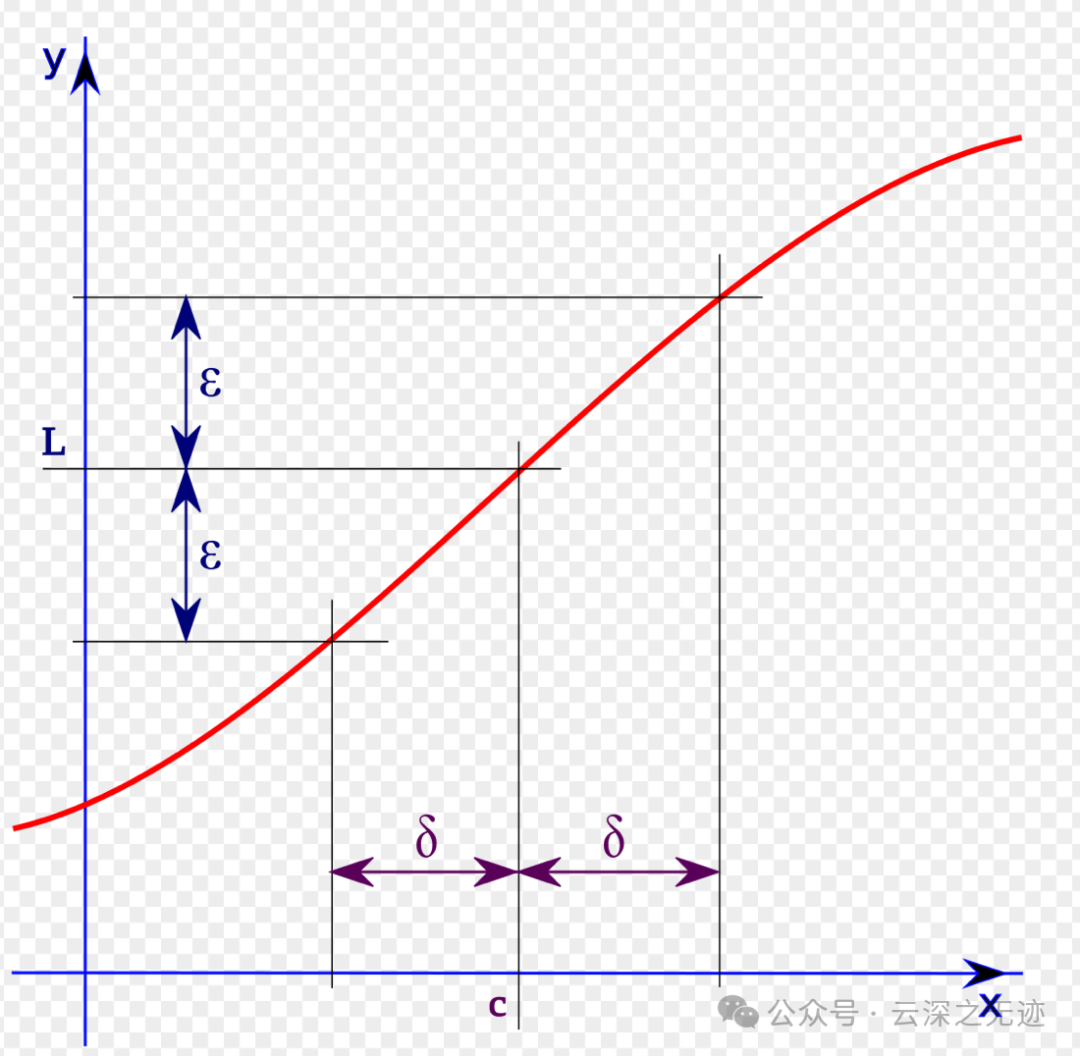
这个是上面的定义的可视化图：只要无限靠近c，函数值就无限靠近L

继续说，如何来表达函数值和极限值的趋近，也就是极限关系呢？就是它们的距离越来越小，距离的表示就是    |函数值-极限|  ，距离一定是正的，加绝对值，如果你说可以是负值，那我劝你还是不要GHS。

也就是说，小于世界上任何一个正数就好了，可能在你的认识里面这个数等于0就是最好的，不行啊，这样一搞不就是是等式了。

那么我们这样说，对任意一个ε（取很小的值），使得 |函数值-极限| ＜ε就说明啦。以上是对函数值无限接近于极限值的描述。

接着就是来说明这个了，这个x为什么会被夹着。

极限是自变量趋于某个值的，这个趋近于的描述应该是一个过程，如何用数学来说明这个趋近的事实。两个点不太行，只有连续才可以表示一个过程。在数学里面使用“区间”才可以表示连续的点。

先设x和a的初始距离为δ，在x靠近a或者是趋近的这个过程中，x和a之间的范围始终在（0，δ）区间里面。

距离我上面说了，可以用差的绝对值来表示，也就是说自变量趋于某个值。

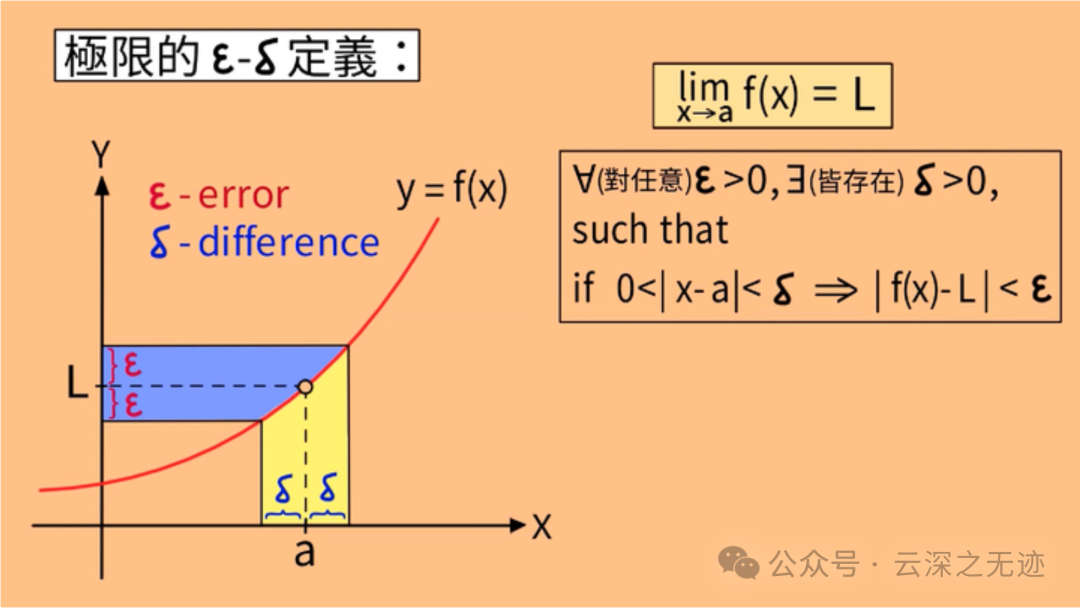
这个图也挺形象

上面的这个不等式也可以说成是邻域，也就是说邻域知道了极限的作用范围。

至于微积分基本上每个定义上，都会加个去心邻域，现在明白了，其实就是为了防止邻域中心没有定义的情况，因为书上的定义定理啥的都得具有一般性，所以它就这样，能够代表所有不管在此点有没有定义的函数，反正是极限，有没有邻域中心都一样。

本来极限的定义就是无限趋向该点，这和在该点有没有定义并没有关系，所以我们只要保证除去该点以外的邻域有定义即可。

这个解释也很酷，说明了邻域的作用其实是一个微小的观察空间

这个也是一个有趣的例子

审核编辑：刘清