ΣΔ(Sigma-Delta)技术详解(上)：离散ΣΔ调制器

Δ技术可以用来实现 ΣΔADC 和 ΣΔDAC ，是高精度、低噪声 ADC/DAC 的主流技术。要理解 ΣΔADC 和 ΣΔDAC ，需要按照以下顺序来学习：

离散ΣΔ调制器 → ΣΔDAC

离散ΣΔ调制器 → 模拟ΣΔ调制器 → ΣΔADC

本文详细讲解离散ΣΔ调制器。阅读后，你就能分析、设计 ΣΔDAC 。

本文会先为读者建立足够的知识铺垫；然后从直观理解和建模分析的角度讲解离散ΣΔ调制器的原理，包括一阶ΣΔ调制器和高阶ΣΔ调制器；最后用 Python 编写和评估一阶、二阶、三阶离散ΣΔ调制器的性能。

本文涉及离散信号处理的知识，需要读者熟悉z变换的一些概念（除非只关注结论）。

如果要进一步理解 ΣΔADC ，还需要阅读 (下) 篇，理解模拟ΣΔ调制器：

ΣΔ(Sigma-Delta)技术详解(下)：模拟ΣΔ调制器73 赞同 · 12 评论文章

目录

Ⅰ 基础元件介绍

Ⅱ ADC的信噪比

Ⅲ ADC过采样技术

Ⅳ 二值调制器

Ⅴ PWM调制器

Ⅵ 离散Δ调制器

Ⅶ 离散一阶ΣΔ调制器

Ⅷ 离散高阶ΣΔ调制器

Ⅸ 离散二阶、三阶ΣΔ调制器

Ⅹ 各种离散二值调制器的实现和评估

Ⅺ 总结

附：一阶、二阶、三阶ΣΔ调制器的Python实现

Ⅰ 基础元件介绍

本节介绍几个离散信号处理中常见的元件，如表1。它们可以用计算机算法实现，也可以用数字电路（比如FPGA）来实现。例如，比例器、加法器、减法器可以用组合逻辑来实现，延迟器可以用D触发器来实现。

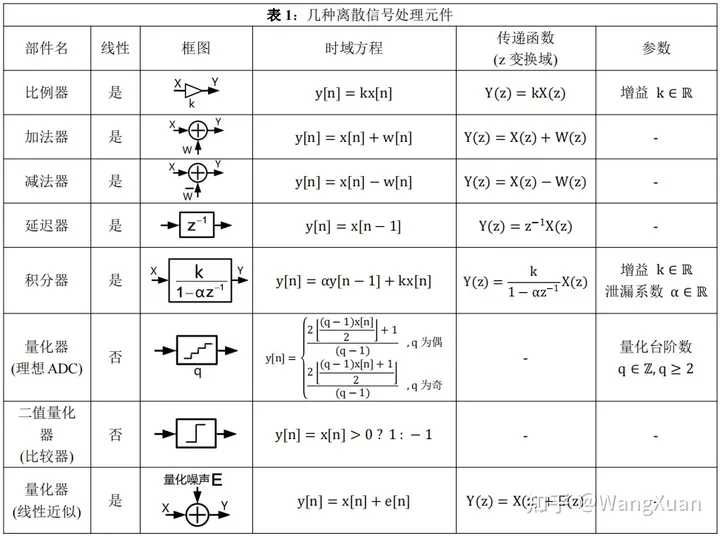
表1中的几种线性元件不必多说。这里我们需要介绍一下这里唯一的非线性元件——量化器。我们知道，对连续信号 x(t) 以采样周期 Ts=1/fs 采样就能得到离散信号 x[n] ：

x[1]=x(Ts),x[2]=x(2Ts),...,x[n]=x(nTs)

把连续信号采样为离散信号……把连续信号采样为离散信号(1)

而再对离散信号的幅度进行量化就能得到数字信号。量化器能把取任意实数的输入信号 x[n] 转化为取有限的 q 个实数的输出信号 y[n] 。

对于 q=2,3,4,16 的量化器，我们绘制它的输入 x[n] 和输出 y[n] 之间函数图如图1。可以看出q是函数图中的“台阶数”。

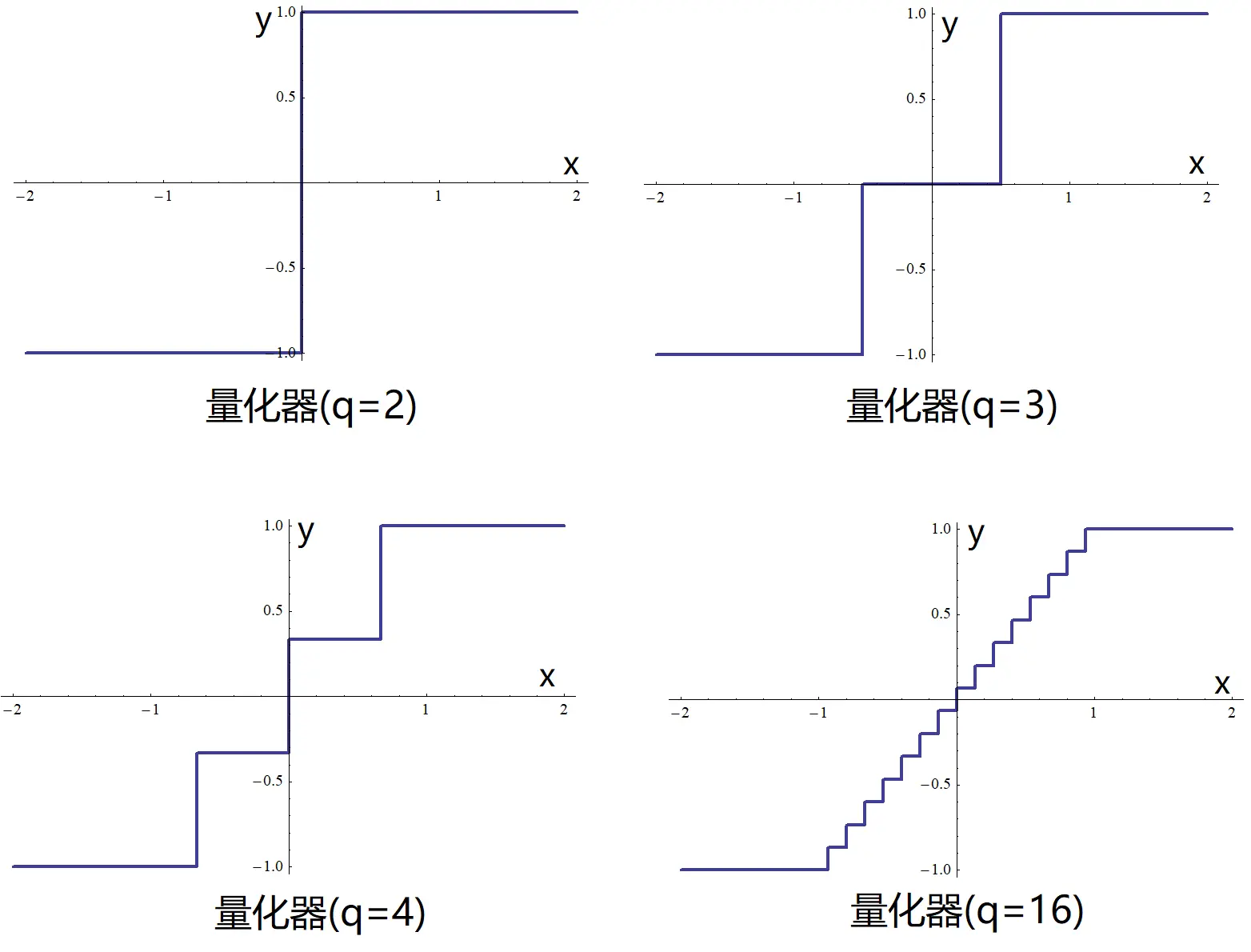
图1：量化器的函数图。其中x轴是量化器的输入，y轴是量化器的输出。

量化器能把取值无限的离散信号转化为取值有限的数字信号，因此也称为理想ADC。比如，理想 10-bit ADC 就是 q=210=1024 的量化器。

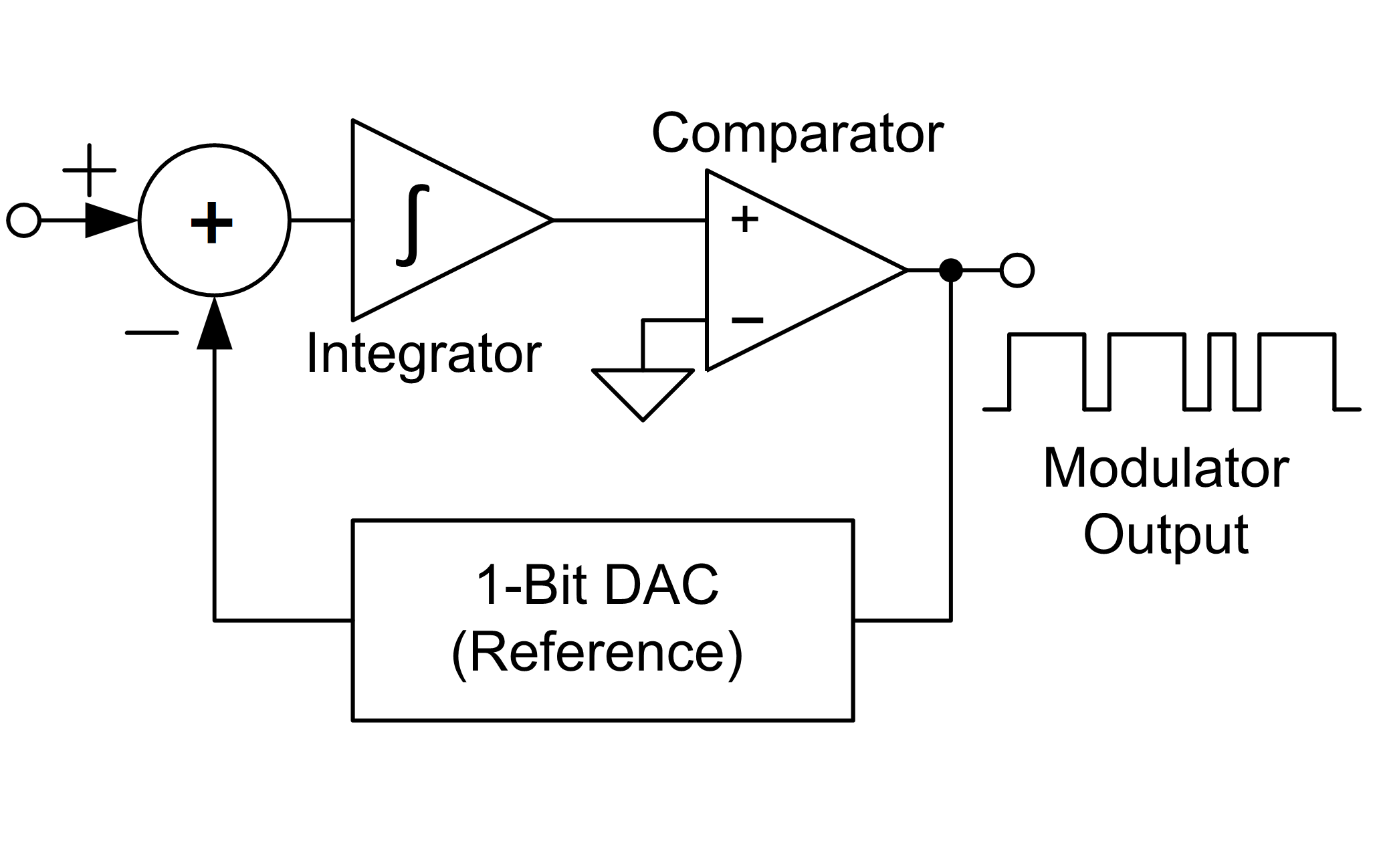
之所以要理解量化器，是因为典型的离散ΣΔ调制器里面会用到一个二值量化器，它是 q=2 的量化器，它对于正数输出+1，对于负数输出-1，可以用比较器来实现。

量化器是非线性元件。众所周知，非线性元件比较难以进行分析。所幸我们很多时候可以把量化器近似为线性元件：

量化器线性近似y[n]=x[n]+e[n]   ……量化器线性近似(2)

其中量化噪声:

e[n]=y[n]−x[n]

这看似是个没什么用的循环定义，不过有时候 e[n] 能近似为与 x[n] 无关的白噪声，此时用线性近似 (2) 就能简化分析。

另外，即使当 x[n] 超出范围 [−1.0,+1.0] 时， y[n] 也会限制在 [−1.0,+1.0] 内，体现出限位器的特性。此时我们说量化器超量程了，此时量化噪声 e[n] 会很大，在设计时要特别注意避免量化器的超量程。

Ⅱ ADC的信噪比

信噪比 (SNR) 是指系统输入的信号功率与系统引入的噪声功率之比，是衡量系统优劣的重要参数，越大越好。

下面我们来分析理想ADC（量化器）的 SNR 。它的噪声全部来自量化噪声 e[n] 。由图1可知，相邻两个量化值之间相差：

δ=2/(q−1)

理想的相邻两个量化值之差的计算公式……理想ADC的相邻两个量化值之差δ的计算公式

在平均情况下，信号均匀分布在相邻两个量化值之间，根据均匀分布的方差，可以得出噪声 e[n] 的功率为：

e2¯=δ212=13(q−1)2

理想的平均噪声功率……理想ADC的平均噪声功率(4)

我们向理想ADC输入一个满量程的正弦信号：

x[n]=sin(ωt+ϕ)

该正弦信号的幅度为 [−1.0,+1.0] ，我们可以算出它的平均功率为：

Psin=limN→∞∑n=0Nx[n]2N=0.5

当该正弦信号 x[n] 通过理想 ADC 时，会叠加量化噪声 (4) ，得到 SNR ：

SNRsin=Psine2¯=0.513(q−1)2=32(q−1)2

理想信噪比……理想ADC信噪比

在工程中，我们习惯用分贝 (dB) 来表示 SNR ：

SNRsin=10log10⁡(32(q−1)2)   (dB)

=10log10⁡(32)+10log10⁡((q−1)2)   (dB)

≈1.76+20log10⁡(q−1)   (dB)

理想信噪比……理想ADC信噪比(5)

已知 N-bit 理想 ADC 的 q=2N ，代入公式(5)可以得到 N-bit 理想 ADC 的信噪比：

理想信噪比SNRsin≈1.76+6.02N   (dB)   ……理想ADC信噪比(6)

实际ADC的噪声来源不止是量化噪声，还有电路引起的热噪声等，因此实际 N-bit 的 ADC 的 SNR 一定小于(6)。

为了评估实际ADC的优劣，我们往往在实验中用满量程正弦波输入实际ADC，测出SNR，然后代入(6)反向计算出N，称为ADC的有效位(ENOB)。ENOB代表了该ADC在测量满量程正弦波时，SNR相当于多少bit的理想ADC。

注意：ENOB并不能代表ADC输入直流时的分辨率，只能代表交流性能，而ADC的直流分辨率位数可能大于或小于它的ENOB。这部分内容不做赘述。

用公式(6)计算理想ADC的SNR前，一定要检查两个条件是否满足：

条件①：ADC未超量程。否则 y[n] 和 x[n] 之差就会很大，量化噪声 e[n] 就不能视作均匀分布于相邻量化值之间，则公式(4)不成立，无法推导出公式(6) 。

条件②：输入信号 x[n] 的幅度要远大于相邻两个量化值之差 δ 。否则量化噪声 e[n] 同样不能视作均匀分布于相邻量化值之间，公式(4)不成立，无法推导出公式(6) 。

注意：对于位数 N 很小的ADC， q 会很小，δ 会很大，条件②很容易被违反。其中二值量化器（ N=1,q=2,δ=2 ）是一个极端，完全无法套用公式(6)来计算SNR，其SNR会比公式(6)算出来的 7.78 dB 小很多。

Ⅲ ADC过采样技术

设我们有一个采样率为 fs 的ADC，然后输入给该 ADC 一个带宽为 fB 的模拟信号。众所周知，ADC 的理论带宽是奈奎斯特带宽 fs/2 ，也即我们要满足 fs/2>fB ，才能保证高频部分不会混叠到低频。

除了要保证 fs/2>fB 外，我们还可以使用 ADC过采样技术来提高SNR。方法是：

选取采样率更快的 ADC （更大的 fs ），让 fs/2 远大于fB ；

然后在 ADC 后加一个带宽为 fB 数字低通滤波器。

考虑到 ADC 的量化噪声和热噪声往往是白噪声，均匀分布于奈奎斯特带宽 [0,fs/2) 内。加了数字低通滤波器后， f∈[0,fB) 内的信号和噪声被保留， f∈[fB,fs/2) 内的噪声被滤掉。因此噪声会降低到原来的 fs/(2fB) ，SNR 会提升 fs/(2fB) 倍：

过采样原始SNR过采样=SNR原始×fs2fB

在分贝标度上我们可以得到：

过采样原始SNR过采样=10log10⁡(SNR原始×fs2fB)  (dB)

原始=SNR原始+10log10⁡fs2fB  (dB)

过采样技术带来的信噪比提升……ADC过采样技术带来的信噪比提升(7)

这就是ADC的过采样技术。其中我们称 fs/(2fB) 为过采样比。

公式(7)告诉我们，采样率 fs 每提升10倍，SNR 就提升 10dB；采样率 fs 每提升4倍，SNR 就提升 6.02dB，也即 ENOB 提升 1bit。

注意公式(7)成立的两个条件：

条件①：使用的低通滤波器足够理想，也即通带和阻带间增益足够陡，阻带的增益足够小；

条件②：ADC 的噪声近似白噪声。

如果ADC的噪声偏红（更多地分布于低频），由于低通滤波器无法滤掉这些低频噪声，则过采样技术就收效甚微，无法获得公式(7)那么多的SNR提升。

反之，若噪声偏蓝（更多地分布于高频），过采样技术就能获得比公式(7)还好的SNR提升，本文要介绍的ΣΔADC 就用了该思路。

作为引子，我们看看对理想 ADC 使用过采样技术达到的效果如何。我们把满幅正弦波 x[n]=sin⁡(2πn/2048) 输入不同 q 值的量化器，得到输出 y[n] 如图2（上）、量化噪声 e[n] 如图2（中）、y[n] 的 262144 个样点的频谱如图2（下），并计算 SNR 展示在表2 第一行。

然后我们用过采样技术，在频谱上截取带宽 f表2 第二行（相当于使用了理想低通滤波器）。根据公式(7)知，这样可让 SNR 提升 18dB，然而从表2 知，当 q 很小时，过采样技术带来的 SNR 提升远不及 18dB。这是因为从图2（中）可知，当量化不够“细腻”，也就是 δ 不显著小于 x[n] 的幅度时，量化噪声 e[n] 与 x[n] 呈强相关，不能被近似为白噪声，而是偏红，导致过采样技术收效甚微。

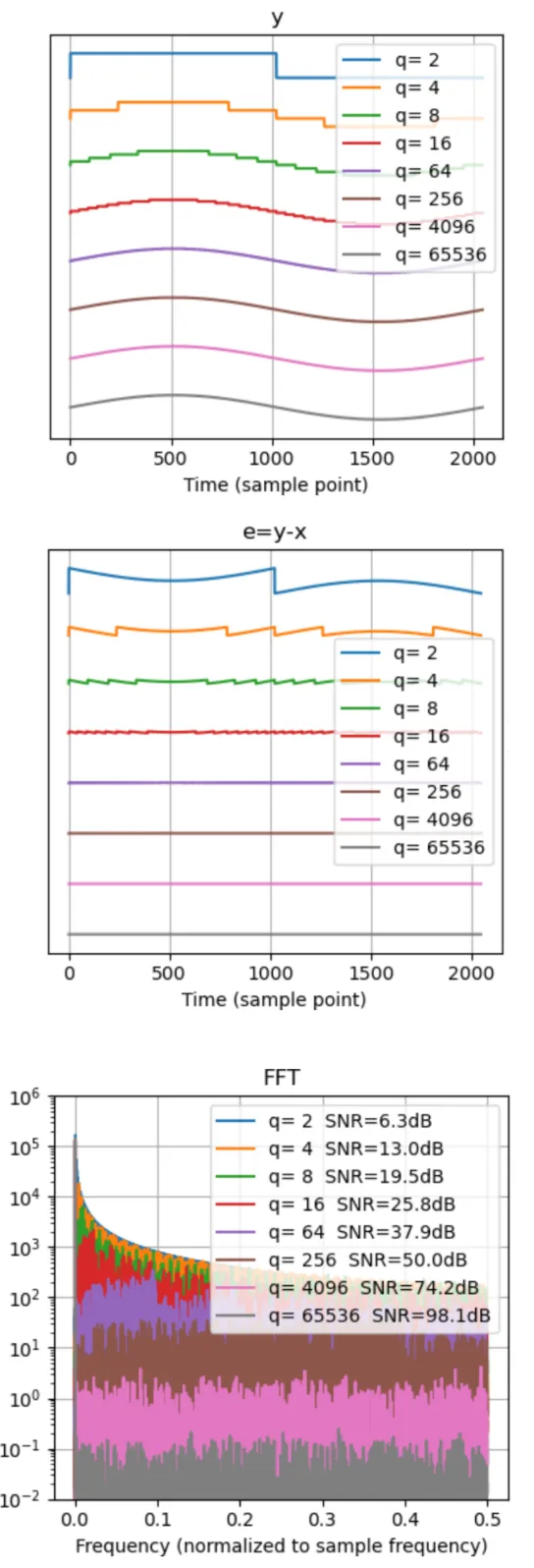
图2：满幅正弦波输入理想ADC得到的时域输出（上）；量化噪声（中）；输出的频谱（下）

Ⅳ 二值调制器

二值调制器并不是一个元件，而是泛指一类能把输入信号转化为二值信号的元件。在本文中，二值信号是指取值仅为 -1.0 或 +1.0 的离散信号，也可以视为1bit数字信号。

衡量二值调制器的性能的方法是看它输出的二值信号是否能在频谱上尽量多的保留其输入信号的信息。具体来说，我们对输入信号和输出信号分别做离散傅里叶变换（FFT），看它们的频谱在一定带宽内是否相似，越相似越好。

上一节介绍的二值量化器就是一种二值调制器，但它的性能并不好，因为其引入的量化噪声 e[n] 主要分布于低频（偏红），和信号混在同一带宽内，用低通滤波器并不能把大多数 e[n] 滤掉。

后文我们会看到几种性能更好的二值调制器（PWM调制器、Δ调制器、ΣΔ调制器）。它们引入的噪声 e[n] 呈现白色或蓝色，用低通滤波器滤掉大多数高频噪声后，可以获得较高的 SNR 。

二值调制器分为两种：

离散二值调制器：输入离散信号，输出二值离散信号 (1bit数字信号) ，可用数字电路或计算机算法来实现。本文后文要讲的PWM调制器、离散Δ调制器、离散ΣΔ调制器都属于离散二值调制器。

模拟二值调制器：输入连续信号，输出二值离散信号 (1bit数字信号) ，可用模数混合电路来实现。(下)篇文章中要讲的模拟ΣΔ调制器就属于模拟二值调制器。

如图3，模拟二值调制器可以用来实现ADC，离散二值化调制器可以用来实现DAC。后级都加了低通滤波器用来滤除二值信号中我们不关心的高频噪声，来尽量还原原始信号。

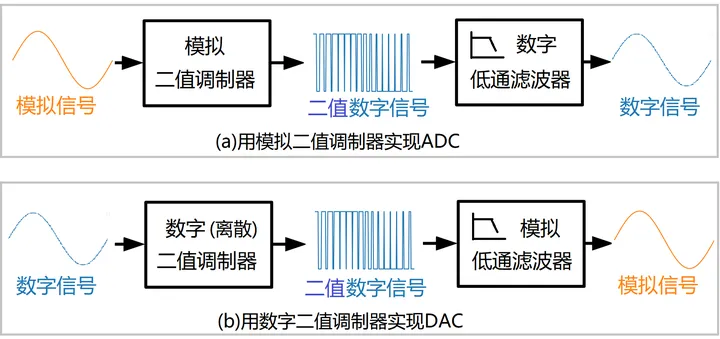
图3：用二值调制器实现ADC和DAC

显然，二值调制器的性能是这种 ADC 和 DAC 关键，因为如果二值调制器性能差，产生的二值信号在我们关心的低频带宽内混杂了过多的噪声，那么即使低通滤波器再理想，也无法滤掉这种噪声。

这也是为什么后文要花大篇幅来分析 离散ΣΔ调制器 ，掌握了离散ΣΔ调制器的分析方法，我们才能设计出 SNR 足够高的 ΣΔDAC 。

相反，图3中的低通滤波器设计相对简单，只要满足通带和阻带间增益足够陡，阻带的增益足够小，它就能从二值信号中尽量滤掉我们不想要的高频噪声，保留低频信号。滤波器的设计是《信号与系统》和《数字信号处理》中的基础知识，而且 MatLab、Python 中有成熟的滤波器设计工具，因此本文不做赘述。

Ⅴ PWM调制器

PWM调制器是一种最直观的二值调制器。PWM调制器用直观的“占空比”法来产生二值信号 y[n] 。如图4，它把相邻 m 个样点视作一个时间片，在时间片内放置 r 个 +1 和 (m−r) 个 -1 ，因此该时间片内的均值是：

y¯=1×r+(−1)×(m−r)m=2rm−1

其中 r 是占空比， 1m 是PWM频率。它们都是算法或数字电路中可以改变的参数。通常我们保持 m 固定，通过改变 r 来让 y¯=x ，也即让输出信号在时间片内的均值等于输入信号：

y¯=x

⇒   2rm−1=x

⇒   rm=x+12

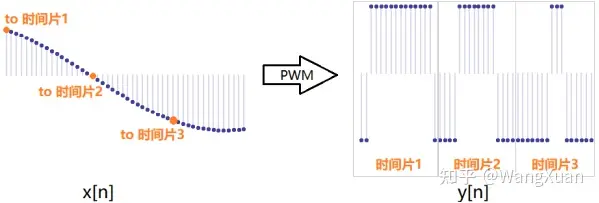
图4：PWM调制

Ⅵ 离散Δ调制器

Δ调制器是另一种二值调制器，是ΣΔ调制器的前身。图6是离散Δ调制器的系统框图，其中Δ调制器只是左半部分，它输出二值信号y[n]。右半部分是一个补偿器，它输出的w[n]不是二值信号。该补偿器的参数需要根据积分器的参数来设计。在现实应用中积分器和补偿器是不同的实现，比如模拟Δ调制器中的积分器是模拟积分器，而补偿器是数字电路实现。

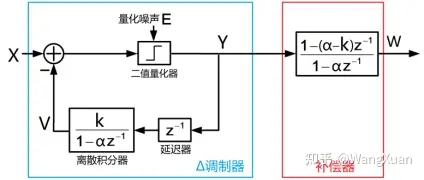
图6：离散Δ调制器的系统框图

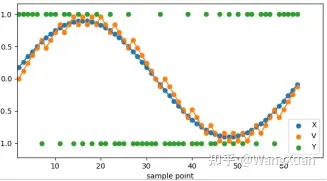
图7：Δ调制器在输入正弦波时的现象

在后文中，约定小写字母 (x[n], v[n], y[n]) 代表时域离散信号，大写字母 (X, V, Y) 代表对应的 z 变换后的信号。

我们先进行直观理解：设 x[n] 是正弦信号，得到各个信号的波形图如图7。可以看到 v[n] 在试图跟随 x[n]，这是因为当 x[n]>v[n] 时，二值量化器会输出 y[n]=+1，而因为 v[n+1]=αv[n]+ky[n] ，只要 α 不是太小，就能让 v[n+1]>v[n] ，也就是让 v[n]增大。同理当 x[n]

有了直观理解后，进行理论分析，首先我们知道时域关系：

v[n+1]=αv[n]+ky[n]   ……(8)

考虑到 y[n]只取+1 和-1，所以 v[n]能达到的最高的变化率与 v[n] 的取值有关，为：

|Δv|max=min((α−1)v,(1−α)v)+k   ……(9)

而满幅正弦波 x[n]=sin⁡(2πnf/fs) 的变化率随着 x[n] 的取值而变化，关系为：

|Δx|max=2πffscos⁡(arcsin⁡x)   ……(10)

为了让 v[n] 能跟随 x[n]，必须保证 |Δv|max>|Δx|max ，即：

min((α−1)x,(1−α)x)+k>2πffscos⁡(arcsin⁡x)   ……(11)

解(11)得Δ调制器必须满足约束：

k2−(1−α)2>(2πffs)2

调制器能成功跟随的条件……Δ调制器能成功跟随的条件(12)

下面我们推导Δ调制器在 z 变换域的传递函数，注意我们把二值量化器进行了线性近似，E 是它的量化噪声。 另外，以下公式中的大写字母都是 z 变换域的复变函数，比如 Y 应写做 Y(z)，这里省略了(z)。

Y=X+E−kz−11−αz−1Y

⇒Y=1−αz−11−(α−k)z−1(X+E)

调制器的传递函数……Δ调制器的传递函数(14)

(14)的传递函数有一个极点 z=α−k ，要让系统稳定，令极点在单位圆内：

调制器稳定的条件−1<α−k<1   ……Δ调制器稳定的条件(15)

从前文的直观叙述我们知道，二值信号 y[n] 包含 v[n] 的增加/减小信息，当 x[n] 是直流时，v[n] 在 x[n]上下跳跃，此时 y[n]在+1, -1 间交替，并不包含直流信息。这一点我们也可以从传递函数(14)来理解，在直流（z → 1）时，由于α一般接近于 1，导致 Y 非常小，说明直接使用 y[n] 作为输出就会丢失 x[n] 的直流部分，因此对Δ调制器来说，加入图6所示的补偿器是必须的，该补偿器的传递函数为 1−(α−k)z−11−αz−1 ，具有积分的效果，可以从 y[n] 中恢复出 x[n] 的直流信息。经补偿后，(14)前面的因子被消掉：

调制器补偿后的传递函数W=X+E   ……Δ调制器补偿后的传递函数(16)

习惯上，把传递函数表示成：

W=HxX+HeE

其中 Hx 称为信号传递函数； He 称为噪声传递函数。

我们发现，经补偿后 Hx=He=1 ，这似乎意味着只要满足约束条件(12)(15)就能随意配置参数α和k，实则不然，因为二值量化器的非线性，实践中会观察到 α=1 时量化噪声 e[n] 近似白噪声，而 e[n] 越小，e[n]越分布于低频。因此实践中往往令 α=1 ，再在(12)(15)的约束下配置一个尽量小的 k 。在模拟Δ调制器设计中，由于一些现实问题，比如运放开环增益并不是无穷大，导致积分器缓慢泄漏，即 α 是一个略小于 1 的值（比如 0.99）都是完全能容忍的。不过 α 不能过小，否则会导致低频噪声很大。

为了验证以上结论，我们在(12)(15)的约束下设计出七种 α, k 的组合如表3。我们编写代码仿真，将正弦波 x[n]=0.9sin(2πn/4096) 输入这些Δ调制器，计算出带宽 f表3。可以看出在 α>0.97 时 SNR 都还不错，但随着 α 继续减小，SNR会持续恶化。

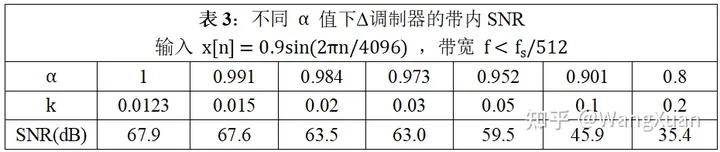
加补偿的Δ调制器的传递函数为 W=X+E 。考虑到当 α 接近 1 时，E 为白噪声，过采样技术带来的 SNR 提升满足公式(7)，即每过采样 4 倍，SNR 提升 6.02dB 。注意：Δ调制器与 1-bit ADC 的区别就在于 1-bit ADC 的量化噪声 E 不是白噪声，导致过采样技术失效；而Δ调制器不会使过采样技术失效。

Ⅶ 离散一阶ΣΔ调制器

对Δ调制器稍作修改就能得到一阶ΣΔ调制器如图8，它后面也有一个补偿器（但不是必须的）。为了方便分析，设积分器无泄漏（α = 1）。实际使用中与Δ调制器同样， α 不能与 1 相差过大，否则影响性能。另外，相比于Δ调制器，反馈回路中多了一个增益 g ，因此ΣΔ调制器有两个参数：k, g 。

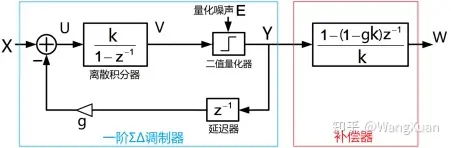
图8：离散一阶ΣΔ调制器的系统框图

我们依然先进行直观理解：设 k=0.3, g=1.2 ，分别考察输入 x[n] 为以下情况时的现象：

直流输入 x[n]=0 ，如图9(左)，当 y[n]=−1 时 u[n]=g ，由于积分器的存在导致 v[n] 上升， 导致二值量化器下次会输出 y[n+1]=1 。反之，当 y[n]=1 时会让 v[n] 下降，导致 y[n+1]=−1 。 总之， y[n] 会在+1 和-1 上反复跳跃。

直流输入 x[n]=0.5 ，如图9(右) ，当 y[n]=−1 时 u[n]=0.5+g ，引起的 v[n] 的上升量为 v[n+1]−v[n]=k(g+0.5) ；同理当 y[n]=1 时引起的 v[n] 的下降量为 −v[n+1]+v[n]=k(g−0.5) 。 这说明每次 v[n] 上升的更多而下降的更少，最终的效果是 v[n] 在 0 附近跳跃，但需要更多的上升步数 和更小的下降步数，导致 y[n]=1 的情况更多，y[n]=−1 的情况更少。

直流输入 x[n]=0.001 ，v[n] 每次的上升量为 k(g+0.001) ；下降量为 k(g−0.001) ， 尽管上升量和下降量相差很小，但毕竟有微小区别，这使得在足够长的时间内 y[n]=1 的情况略多， y[n]=−1 的情况略少。这说明理论上一阶ΣΔ调制器有无限精确的直流分辨率！这是Δ调制器不具备的。 不过这依赖于足够多的样点以及后级数据处理手段。

正弦输入 x[n]=0.9sin⁡(2πn/64) ，如图10，可以看到当 x[n] 较大时 y[n]=1 的情况更多；当 x[n] 较小时 y[n]=−1 的情况更多。

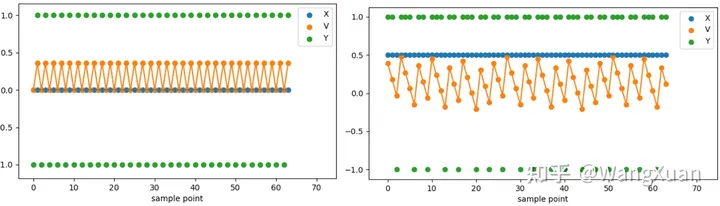
图9：一阶ΣΔ调制器在输入 x[n]=0 (左) 和 x[n]=0.5 (右) 时的现象

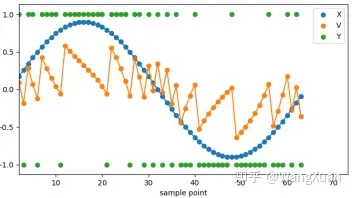
图10：一阶ΣΔ调制器在输入正弦波时的现象

下面我们根据图8推导ΣΔ调制器的传递函数，注意二值量化器被进行了线性近似，E 是它的量化噪声：

Y=E+V

⇒Y=E+k1−z−1U

⇒Y=E+k1−z−1(X−gz−1Y)

⇒Y=kX+(1−z−1)E1−(1−gk)z−1

一阶调制器的传递函数……一阶ΣΔ调制器的传递函数(17)

(17)有一个极点 z=1−gk ，要让系统稳定，令极点在单位圆内：

一阶调制器稳定的必要条件0

我们也可以在ΣΔ调制器后加入补偿器。这样可以消掉(17)的分母：

W=1−(1−gk)z−1kY

⇒W=1−(1−gk)z−1k×kX+(1−z−1)E1−(1−gk)z−1

⇒W=X+(1−z−1)kE

一阶调制器补偿后的传递函数……一阶ΣΔ调制器补偿后的传递函数(18)

实践中 gk 并不会设的太小，因此(17)中的分母 (1−(1−gk)z−1)−1 几乎不影响低频（ z→1 ）的相移和增益的平坦性，因此ΣΔ调制器的补偿器不是必须的，通常我们省略掉补偿器，而不像Δ调制器必须进行补偿。

现在假设我们不加补偿，也即直接使用图8中的 Y 作为输出。根据(17)，我们可以得出ΣΔ调制器的信号增益和噪声增益：

Hx=k1−(1−gk)z−1

He=(1−z−1)1−(1−gk)z−1

调制器的信号传递函数和噪声传递函数……ΣΔ调制器的信号传递函数Hx和噪声传递函数He  (19)

考虑到我们只关注低频，也即 z 在单位圆上接近 z=1 的位置，此时噪声传递函数 He 趋近于一 阶无穷小，这说明如果我们关心的信号 x[n] 分布于低频，则 ΣΔ 调制器只会引入很小的噪声，SNR很高。

为了直观说明这个特点，我们使用《信号与系统》中学过的频率响应法来画出ΣΔ调制器的噪声频谱 (噪声幅频特性曲线)。具体方法是：把 z=exp⁡(j2πf/fs) （z 取单位圆上的点）代入(19)，绘制 |He| 的函数图，得到如图13中的蓝线，可以看出 |He| 随着 f 的减小而减小，这说明：如果图8中的二值量化器量化噪声 E 是白噪声，则ΣΔ调制器输出的噪声偏蓝。因此只要我们关注的频率足够低，带内噪声就会很小，得到的 SNR 也会非常高。

Ⅷ 离散高阶ΣΔ调制器

将一阶ΣΔ调制器中的减法-积分器结构复制M份就能得到M阶直连型ΣΔ调制器如图12。推导其传递函数：

Y=E+k1−z−1(−gz−1+k1−z−1(−g2z−1+k1−z−1(...k1−z−1(−gMz−1Y+X))))

⇒Y=z−1−(1−gk)(gk)M+1z−1−(1−gk)(1−z−1)M+1(kMX+(1−z−1)ME)

阶直连型调制器的传递函数……M阶直连型ΣΔ调制器的传递函数(20)

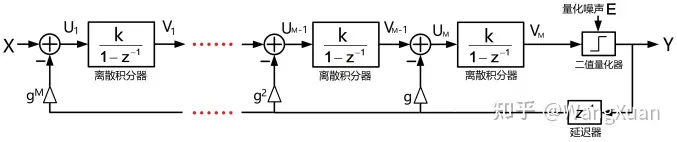
图12：离散M阶ΣΔ调制器的系统框图

现在考察该传递函数(20)的稳定性，也就是看左边的因子项的极点是否都在单位圆内。我们利用数值计算得到一阶到五阶的稳定条件如表4。注意这是线性系统的稳定条件！由于因为量化器的非线性，该系统还存在非线性失稳的可能，因此表4只是系统稳定的必要条件。

然后考察幅频特性，若我们补偿掉(20)中左边的因子，得到信号传递函数 Hx=kM ，噪声传递函数 He=(1−z−1)M 。显然 He 在 z=1 处有n重零点，这意味着当频率很小（ f<图13。可以看出在带宽 f<0.16fs 内，阶数越高，带内噪声一定越小。

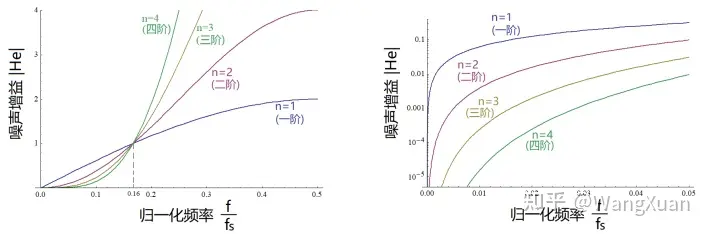
图13：理想ΣΔ调制器的理论噪声增益：奈奎斯特带宽内的线性坐标（左）；低频内的对数坐标（右）

这看似是个非常好的结论，意味着我们只要按图12的结构堆叠阶数，理论上就能在我们关心的低频带宽内得到无限低的噪声。然而，在阶数 M>3 时，量化器的非线性往往会产生非线性失稳：我们可以把量化器看作一个增益元件，当量化器的输入 vM[n] 越大时，增益反而越小，因为系统构成环路，增益过小会导致环路失稳。除了非线性失稳问题，高阶情况下各积分器的输出 vi[n] 的范围往往不易控制，若不精心设置系统，很可能导致 vi[n] 远超出范围 [-1,+1] ，在实际电路实现中，可能超出器件的线性工作区。

所幸我们有很多办法来规避这些问题，让高阶ΣΔ调制器变得可行：

配置图12中的增益参数 。比如增加 g 来让环路有足够的增益；减小 k 来控制 vi[n] 的范围。实际上各个积分器的增益 k 可取不同值，反馈路径的增益 g 也可取不同值，来达到更优的结果。本文只考虑它们都相同的情况。

在图12的基础上增加新的信号通路（比如前向通路）来达到同样的目的。

抛弃图12的积分器高阶级联结构，而是使用多个低阶ΣΔ调制器级联来等效出高阶的效果。

方法2和3更复杂且效果好，被广泛用在当今的ΣΔADC集成芯片中。下文我们仅仅简单地用方法1来让二阶和三阶ΣΔ调制器变得可行。

Ⅸ 离散二阶、三阶ΣΔ调制器

根据图12，二阶ΣΔ调制器的系统框图如图14；三阶ΣΔ调制器的系统框图如图15。

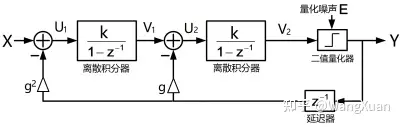
图14：离散二阶ΣΔ调制器的系统框图

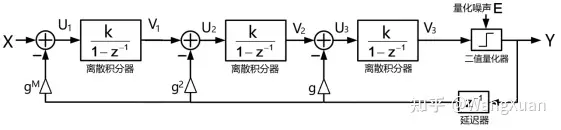
图15：离散三阶ΣΔ调制器的系统框图

根据公式(12)得出，二阶ΣΔ调制器的传递函数：

Y=k2X+(1−z−1)2E1−(1−gk)(2+gk−z−1)z−1   ……(21)

以及三阶ΣΔ调制器的传递函数：

Y=k3X+(1−z−1)31−(1−gk)(3+2gk+g2k2−(3+gk)z−1+z−2)z−1   ……(22)

如表5，笔者用代码仿真的方法确定了能够稳定，且效果较好的二阶ΣΔ调制器的参数 (M=2, k=0.6, g=1.2)，以及较好的三阶ΣΔ调制器的参数 (M=3, k=0.3, g=1.3)。为了帮助直观理解，我们用该二阶和三阶ΣΔ调制器绘制了一段时域波形如图16和图17 。

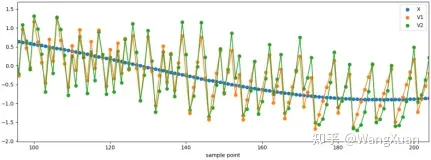
图16：二阶ΣΔ调制器在输入正弦波时的现象

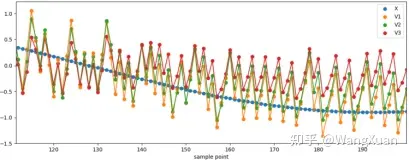
图17：三阶ΣΔ调制器在输入正弦波时的现象

然后我们考察这些配置下的噪声传递函数。把我们选择的一阶ΣΔ调制器的参数 (M=1, k=0.45, g=1.2) 、二阶ΣΔ调制器的参数(M=2, k=0.6, g=1.2) 、三阶ΣΔ调制器的参数(M=3, k=0.3, g=1.3) 分别代入 (17)、 (21) 和 (22) 并绘制噪声传递的幅频曲线 |He| ，如图18 ，可以看出，阶数越高，噪声增益越低。

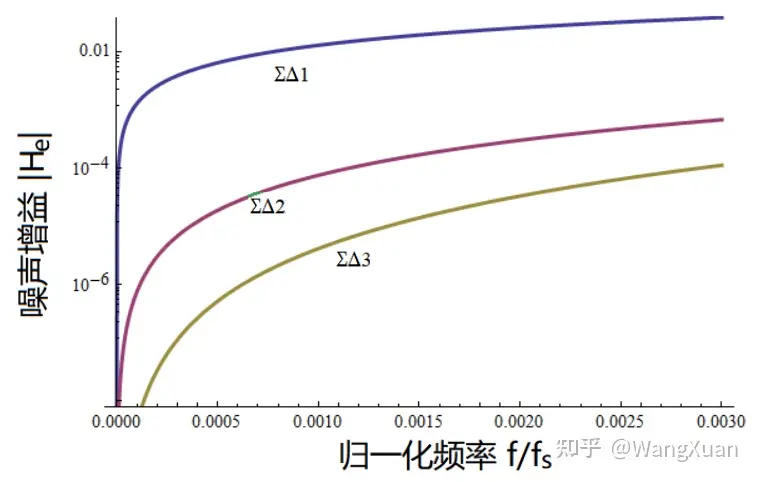
图18：本文的实验使用的几种ΣΔ调制器配置（见表5）的理论噪声增益

Ⅹ 各种离散二值调制器的实现和评估

本节对几种离散二值调制器进行评估。我们用 Python 3 实现了上文中的二值调制器（部分代码见附录），并找到几种效果不错的配置如表5。

直观起见，取输入信号 x[n]=0.9sin(2πn/256) ，绘制各调制器的输出如图19，样点的数量为256。可以看出：除了Δ调制器外，其余的调制器均体现出 x[n] 越大则输出的均值越大的规律。而Δ调制器要经补偿后才能看出这个规律。

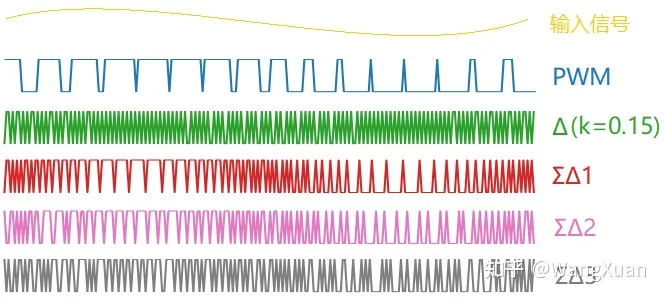
图19：输入为 x[n]=0.9sin(2πn/256) 时各个调制器产生的输出

然后取输入 x[n]=0.9sin⁡(2πn/2048) 绘制 218 个点的频谱如图20 。可以看出不同的调制器有不同的底噪，Δ调制器好于PWM调制器；ΣΔ调制器好于Δ调制器；高阶ΣΔ调制器好于低阶ΣΔ调制器。另外，Δ调制器的底噪呈现白色，而所有ΣΔ调制器的底噪都呈现出频率越低，噪声越小的现象，这符合之前的理论分析。

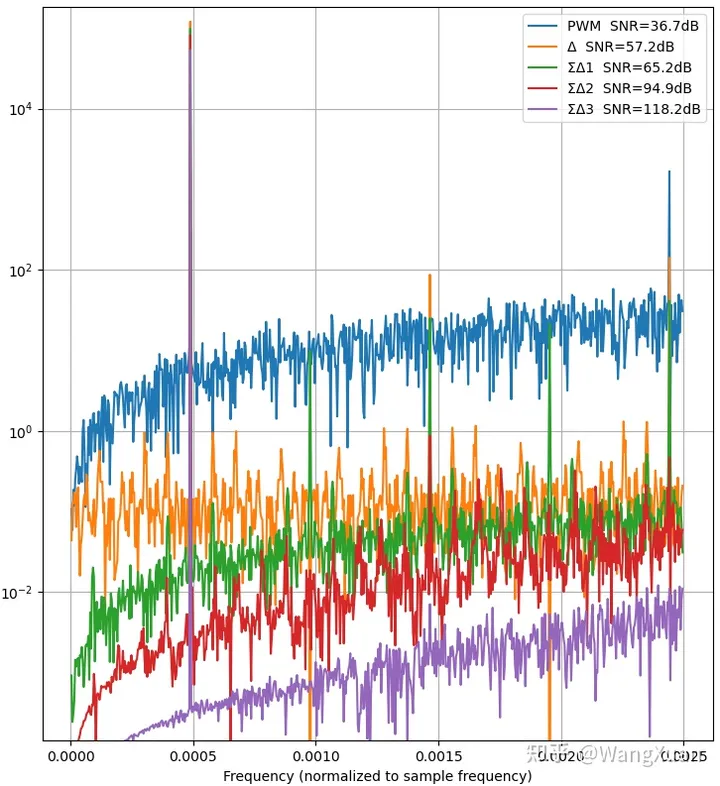
图20：输入为 x[n]=0.9sin(2πn/2048) 时各个调制器输出的信号的频谱（2^18个点）

最后，取不同的正弦波幅度和频率，用 220 个点的频谱计算带宽 f表6。注意：在计算频谱和SNR时，为了防止频谱泄漏，时间窗口都截取 x[n] 的完整周期，且窗口长度是周期长度的2的次幂倍。

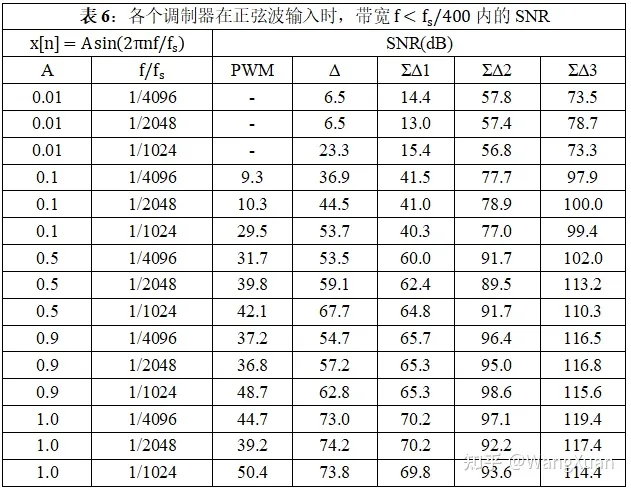
Ⅺ 总结

本文带读者“入门”了ΣΔ技术，内容包括：

理想ADC的信噪比计算。

ADC过采样技术；以及其在量化阶数q较小时的局限性——量化噪声不再是白噪声，导致过采样技术收效甚微。

离散二值调制器、模拟二值调制器的基本概念；以及如何用前者实现DAC，用后者实现ADC。

最直观的二值调制器——PWM调制器。

ΣΔ调制器的前身——Δ调制器，分析出其量化噪声呈白噪声，从而让过采样技术生效。

一阶离散ΣΔ调制器，分析出其量化噪声偏蓝，从而让过采样技术获得奇效。

高阶离散ΣΔ调制器：从z变换的角度解释阶数高的好处，也指出了高阶面临的稳定性问题。

比较了离散PWM调制器、Δ调制器、离散一二三阶ΣΔ调制器的信噪比。

离散ΣΔ调制器可以实现ΣΔDAC。如果对ΣΔADC的基础——模拟ΣΔ调制器感兴趣，请阅读(下)篇：

ΣΔ(Sigma-Delta)技术详解(下)：模拟ΣΔ调制器73 赞同 · 12 评论文章

附：一阶、二阶、三阶ΣΔ调制器的Python实现

 

# -*- coding:utf-8 -*-
# python3
# 离散ΣΔ调制器（一阶、二阶、三阶）
import numpy as np
import matplotlib.pyplot as plt

# 运行参数 --------------------------------------------------------------------------------
MARGIN     = 16384                                                          # 初始丢弃点数
TIME       = 1048576                                                        # 有效点数
PERIOD_X   = 2048                                                           # 正弦周期
AMP_X      = 0.9                                                            # 正弦幅度
BAND_RATIO = 0.5/240                                                        # 过采样比

MODULATORS = [       # 参与评估的调制器配置，格式: [ 名称 , 阶数 , k   , g   ] ------------
    ['ΣΔ1' ,    1 , 0.5 , 1.2 ] ,
    ['ΣΔ2' ,    2 , 0.6 , 1.2 ] ,
    ['ΣΔ3' ,    3 , 0.3 , 1.3 ] ,
]

def sigma_delta_mod(X, M, k, g):      # ΣΔ 调制函数 ---------------------------------------
    Y = np.zeros(len(X))                                                    # 输出信号
    V = np.zeros([M, len(X)])                                               # 中间信号
    for t in range(len(X)):                                                 # 遍历时间
        V[0][t] = V[0][t-1] + k*(X[t] - Y[t-1]*g**M )                       # 积分操作
        for m in range(1, M):                                               # 遍历阶数
            V[m][t] = V[m][t-1] + k*(V[m-1][t] - Y[t-1]*g**(M-m))           # 积分操作
        Y[t] = 1.0 if V[M-1][t] > 0 else -1.0                               # 量化操作
    return Y

if __name__ == '__main__':            # 主程序 --------------------------------------------
    X = np.sin(np.arange(MARGIN+TIME)*2*np.pi/PERIOD_X) * AMP_X             # 构造正弦波
    for (label, M, k, g) in MODULATORS:
        Y = sigma_delta_mod(X, M, k, g)                                     # 调制
        Y = Y[MARGIN:]                                                      # 丢弃边界
        FFT_A = np.abs(np.fft.fft(Y))[1:int(TIME*BAND_RATIO)] + 10e-8       # 计算频谱
        FFT_F = np.arange(1,int(TIME*BAND_RATIO)) / TIME                    # 计算频谱横轴
        peak = np.argmax(FFT_A)                                             # 计算峰值
        snr = 1.0/(sum(FFT_A**2)/sum(FFT_A[peak-4:peak+4]**2)-1.0)          # 计算SNR
        plt.plot(FFT_F, FFT_A, label=label )
        print('%s  SNR=%.1fdB' % (label, 10*np.log10(snr) ) )
    plt.xlabel('Frequency (normalized to sample frequency)')
    plt.yscale('log')
    plt.legend()
    plt.grid(True)

 

 

审核编辑 黄宇