本振相噪在射频收发系统中的影响

昨天，有位号友问我本振相噪计算的问题。

这个问题，在以前的公众号文章上，有描述到过，具体如下图所示。

核心思想，就是把相噪和信号都看成单独的信号，通过混频器的时候，就是信号相乘。

这个思想，其实不止用于上述输出相噪的计算。

只要涉及到了混频器和本振，都差不多可以应用这种思想。

(3)

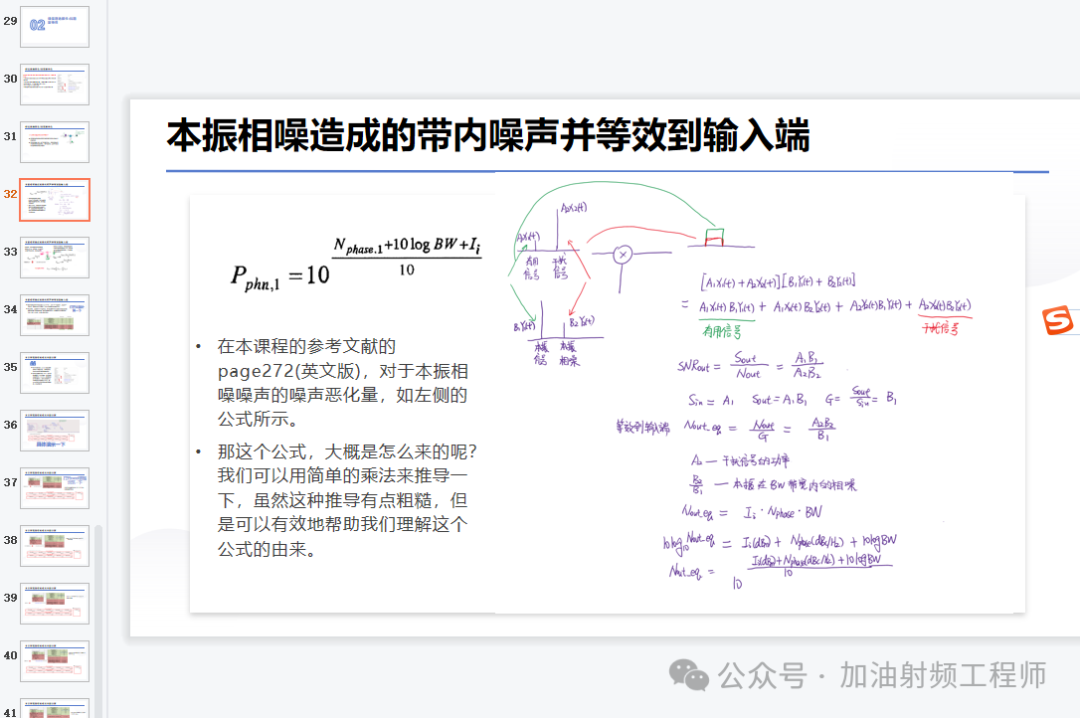
比如说，接收机的抗干扰性能，相关计算公式的由来，也是基于这个思想，就如在底部海报所示的课程中有讲到的那样。

在[1]中的page272页中的抗干扰性能的公式，可以大概用这种思想推导出来。

(4)

然后，还有本振相噪与链路信号的EVM之间的关系。

那要了解这个，其实是分两步走，第一步是本振相噪与输出SNR之间的关系，第二步，就是输出SNR与EVM之间的关系。

首先看，本振相噪与输出SNR之间的关系。

本振相噪与输出SNR之间的关系，其实就类比于在文章开头，号友的问题。

不过，这边的噪声，需要在信道带宽内做积分，不再是单独的某一偏移频率处的值。

先积分算出，在某一带宽内的相噪的总和，进而算出本振的SNR，这样就能算出输出信号的SNR。

如果说，输入信号的SNR远优于本振相噪的SNR，假设为无限大，那么由(2)中的公式，就能推出输出信号的SNR=本振信号的SNR。

 接着看，输出SNR与EVM之间的关系[2]。

EVM是衡量星座图中，理想点与实测点之间误差的RMS值，假设，实测点为Sn，理想点为S0,n，相应的坐标如下图所示。

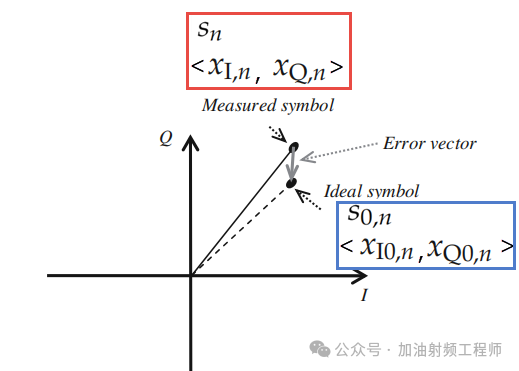
所以EVM可以用下式进行表示：

nI,n和nQ,n分别表示噪声的I分量和Q分量，为理想点向量与测量点向量的差值。

所以从上式可以看出：

两步连起来，就可以得到，本振相噪对输出信号EVM的影响。

(5)

所以，看起来是三个不同的问题，三个不同的应用场景，光看最顶层的公式的话，三者之间并没有什么联系。

但是，如果往底层挖的话，发现这三者都是基于同一种思想，同一个公式，因为这三个都是与混频器的数学模型相关。

审核编辑：刘清