用FPGA实现双调排序的方法（2）

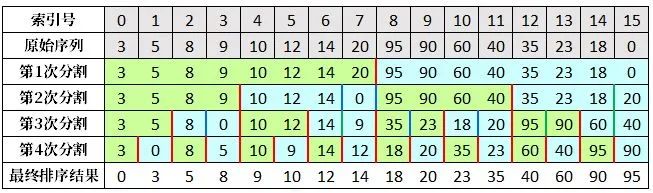
在上篇文章中我们介绍了如何对双调序列进行排序，操作过程如下图所示。

其特征是每次分割都是将原始的序列分成两个等长序列。

例如：原始序列长度为16，第1次分割将其分为2个长度为8的序列；第2次分割将第1次分割的排序结果（长度仍为16）分为4个长度为4的序列；第3次分割将第2次分割的排序结果分为8个长度为2的序列；第4次分割将第3次分割的排序结果分为16个长度为1的序列。

图中相邻的绿色标记和蓝色标记序列构成一组进行比较。

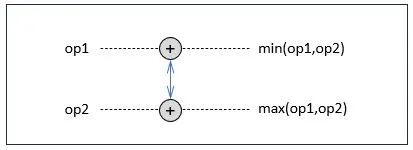
为进一步说明，我们定义操作符Å，如下图所示。

两个操作符Å由双向箭头连接，表示彼此之间共享数据，即下方的Å可接收上方的Å对应操作数op1，同时上方的Å可接收下方的Å对应操作数op2。

位于上方的Å输出op1与op2中的较小者，位于下方的Å输出op1与op2的较大者，简言之Å表示对两个输入数据进行升序排序。

此外，还有一个关键点就是图中虚线的含义。

可以看到op1与min(op1,op2)在一条直线上，op2与max(op1,op2)在一条直线上。

同一条直线上的两个数据其位置是相同的。

即若op1是0号数据，那么min(op1,op2)也必须放到0号位置上，这就是所谓的原位（In-place）运算。

在Å操作符的定义下，长度为16的双调序列的排序过程如下图所示。

图中第1列为二进制数，表示序列中每个元素在序列中的位置也就是地址，用于体现原位运算的特征。

整个排序过程分为4个阶段完成对应图中的Stage 0~Stage3。

在Stage 0中，Å的两个操作数的地址间距为8（例如，3来自0号地址，95来自8号地址）；在Stage 1中间距为4；在Stage 2中间距为2；在Stage 3中间距为1。

审核编辑：刘清