什么是理想的运算放大器？运算放大器的基本应用

什么是运算放大器？

1、什么是运算放大器？ Op-amp”表示“运算放大器”。之所以称为运算放大器是因为其应用于各种运算操作，例如比较、加法、减法、微分和积分等各类运算。

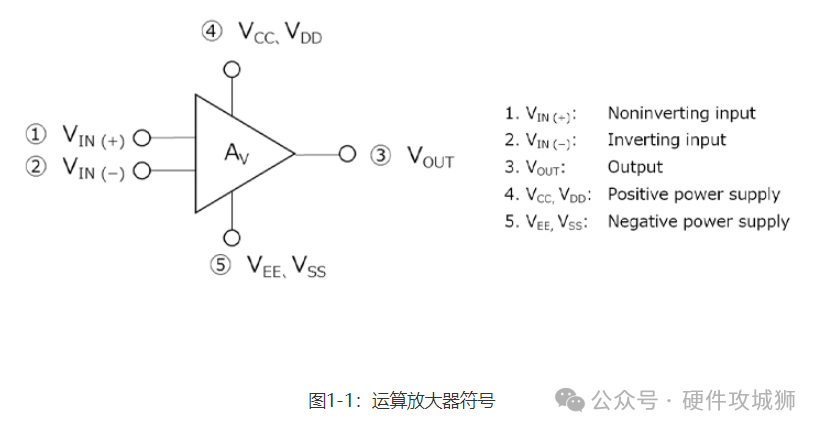
图1-1显示了运算放大器的电子符号。运算放大器有五个端子：1）同相输入；2）反相输入；3）输出；4）正电源；及5）负电源。这里“反相”和“同相”表示相对于输出的极性。

施加于同相输入端的电压相对于反相输入电位放大了AV倍。输出端与同相输入端具有相同的相位。

施加于反相输入端的电压相对于同相输入电位也放大了AV倍。输出端与反相输入端具有相反的相位。

因此，输出端提供的电压等于反相输入端与同相输入端之间的电压差乘以AV。因此，当反相输入端与同相输入端具有相同电压和相位时，输出电压变为零。当反相输入端与同相输入端具有相同电压但相位相反时，输出端与同相输入端同相，所得到的电压等于二者的电压差乘以AV后的两倍。

尽管结构很简单，但运算放大器仍具有接近理想状态的放大器特性。因此，运算放大器广泛适用于各种物联网家用电器和其它电子应用领域的各类用途。例如，运算放大器用于放大来自传感器和测量仪器的模拟信号。

1-1运算放大器的特性（什么是理想的运算放大器？） 通常，放大器应既不影响前级电路，也不受后级电路影响。因此，放大器应具有高输入阻抗和低输出阻抗。

运算放大器的特性恰好接近这些要求。下面比较了理想和实际的运算放大器：

尽管现实中不存在理想运算放大器，但您可在设计阶段的早期假设理想运算放大器。但在进入详细设计阶段后，您应考虑理想运算放大器与实际运算放大器之间的差异。
例如，如果运算放大器的输入阻抗较低，则其输入电压来自该运算放大器的输入阻抗以及前级设备的输出阻抗。运算放大器的低输入阻抗也会影响其反馈回路。如果运算放大器的输出阻抗较大，则其输出电压来自该运算放大器的输出阻抗及其负载的阻抗。

但在典型应用中，运算放大器的输入阻抗与前级电路的输出阻抗相比可忽略不计，而运算放大器的输出阻抗与后级负载的阻抗相比也可忽略不计。因此，这些阻抗通常没有重大影响。上面显示的其它参数亦如此。

但有必要在创建详细设计时检查其影响。

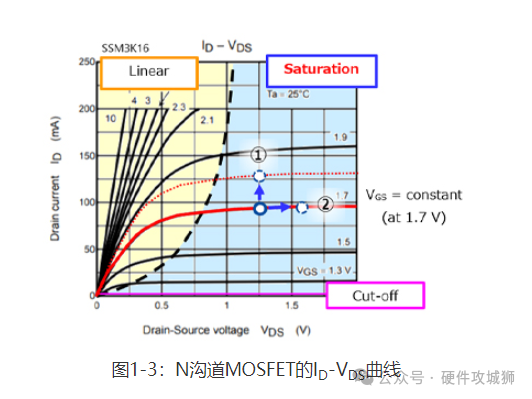
1-2运算放大器的内部操作 图1-2显示了运算放大器的简化等效电路。如您所见，运算放大器由多个MOSFET组成。为使CMOS运算放大器正常工作，这些MOSFET必须在饱和区工作。图1-3显示了MOSFET的饱和区。

MOSFET在该区域内的工作方式如下： 随着栅极-源极电压的升高，漏极电流增大。 随着漏极-源极电压的升高，漏极电流略微增大。漏极电流的细微变化会引起漏极-源极电压的显著变化。

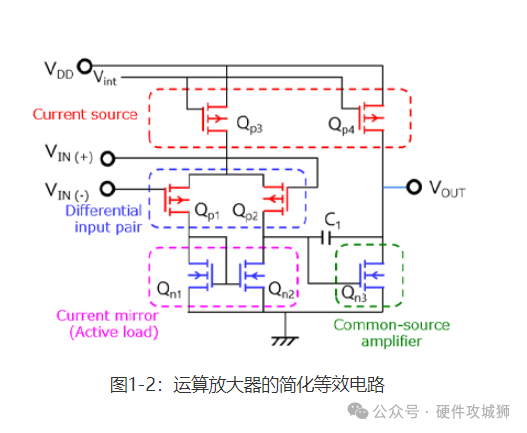
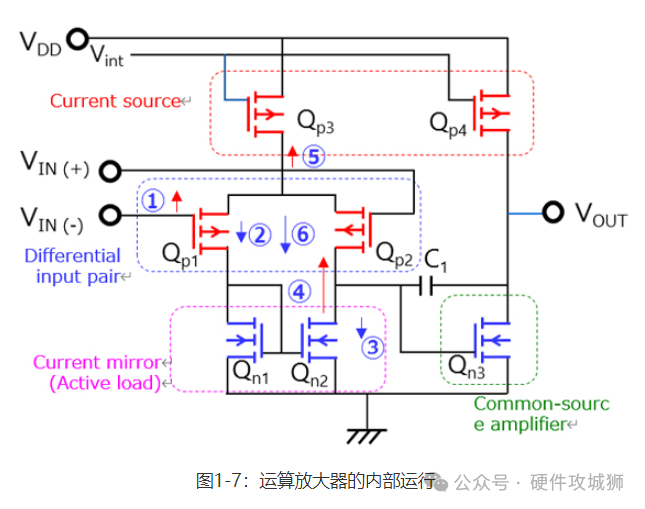
运算放大器各部分的功能如下： 差分输入对：放大VIN (+)输入端与VIN (-)输入端之间的电压差 电流镜：为构成差分输入对的Qp1和Qp2提供等量电流。电流镜用作差分输入对的负载电阻。电流镜的输出端（即差分输入对的漏极端子）通常具有高阻抗，很难用典型电阻器获得这么高的阻抗。因此，第一级差分放大器具有高增益。这种由晶体管构成的电阻负载称为有源负载。

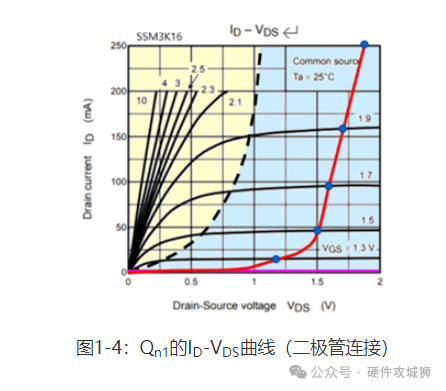
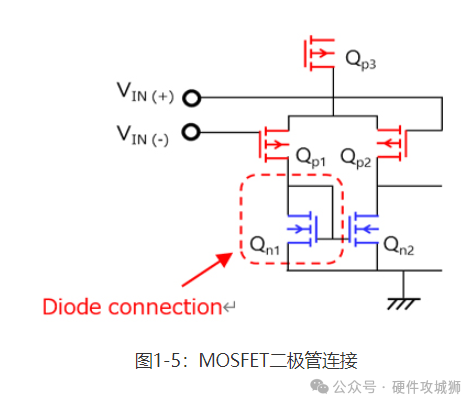
电流源：确定流向差分输入对和共源放大器的电流量。电流源用作共源放大器的有源负载。 共源放大器：为连接至输出端的外部负载提供驱动电流，并补偿第一段差分放大器的增益。 在介绍运算放大器的操作之前，我们先讨论电流镜中Qn1的漏极电压。Qn1的漏源电压（VDS_n1）与漏极-栅极电压（VDG_n1）相等。图1-4显示了满足VDS = VDG的条件。由于生成的曲线看似二极管的IF-VF曲线，故Qn1的连接称为二极管连接。在图1-4中，漏极电流较大，因为它是具有大沟道面积的分立N沟道MOSFET的ID-VDS曲线。IC的内部MOSFET的漏极电流比该电流低两至三个数量级。

如图1-4所示，当漏极电流超过某点（当VDS为1.5V或更高时）后，漏极电流的细微变化几乎不会影响漏源电压。

接下来，我们来看下电流源的工作原理。首先，我们来考察一个无电流源的电路，如图1-6所示。后续共源放大器与先前的运算放大器相同。

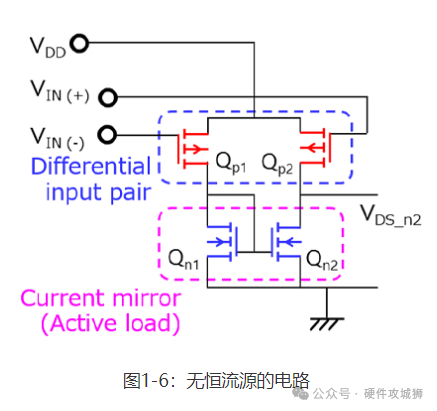
对差分输入端VIN(+)和VIN(-)施加相等的电压（VDD – VIN）。故VSG = VIN。此时，当漏极电流（ID_p1）导通时，Qp1的漏极电压稳定在VSD_p1＋VDS_n1＝VDD的电压处。由于ID_p1被电流镜复制，由Qp2和Qn1组成的电路与其具有相同的电压关系。
假设施加于VIN(+)和VIN(-)的电压升高了ΔV，增至（VDD – VIN + ΔV）。由于图1-6的电路有一个电流镜，故等量电流流向差分输入对。但如果没有电流源，流向差分输入对的电流会等量减少。因此，连接至共源极放大器的Qn2的漏源电压也相应降低。

相当于降低了共源放大器Qn3的栅极-源极电压（VGS_n3）。共源放大器有一个电流源（Qp4），该电流源使漏源电压（VDS_n3）升高以抵抗VGS_n3的下降，从而保持电流恒定。换言之，即使VIN(+)和VIN(-)输入端具有相同电压和相位，输出电压（VOUT）也会升高。当数据表中所示范围内的共模输入（相同输入电压）施加于VIN(+)和VIN(-)时，运算放大器必须具有恒定输出。图1-6所示的电路无法满足此要求。 接下来，我们来看下带有恒流源（Qp3）的电路（图1-2所示的电路）。例如，假设施加于VIN(-)和VIN(-)的输入电压升高了ΔV，增至（VDD – VIN + ΔV）。由于此电路有一个电流源，故流入差分输入对的电流保持不变。因此，Qn1的漏源电压（VDS_n3）保持不变。同理，VDS_n2保持不变。因此，对于共模输入电压，输出电压均保持恒定。

（Qp3的VSD_p3补偿ΔV。由于电流源的源漏电压发生变化，故流向差分输入对的电流也会相应变化。由于电流源的漏源电压发生变化，故漏极电流（ID）也相应变化。但ID仅随VDS略微变化。故ID无显著变化。）

因此，当共模输入电压施加于VIN(+)和VIN(-)时，电流源的作用就是保持输出电压恒定。   接下来，我们来看下对VIN(+)和VIN(-)施加不同电压的情况。 假设VIN(+)和VIN(-)最初具有相同电压（VDD – VIN），然后VIN(-)电压升高了ΔV。 VSG_p1降低，导致ID_p1减小了ΔIp1。然而，如上所述，Qn1具有二极管连接。因此，VDS_n1保持不变。故Qp1的漏极电压保持不变。 电流镜将减少的ID_p1复制到Qn2的漏极电流（ID_n2）。 这自相矛盾，因为电流源中Qn3的漏极电流（ID_p3）保持不变。因此，Qn2的漏极电压（VDS_n2）升高，以增大流经Qn2的电流。 您可能认为VDS_n2的升高会导致VSD_p2降低，从而导致ID_p2减小。但请注意，来自电流源（ID_p3）的电流保持不变。由于ID_p1减小了ΔIp1，故ID_p2应增大而非减小。因此，Qp2的源极电压升高。 Qp1的源极-栅极电压（VSG_p1）升高，导致其漏极电流（ID_p1）增大。 ID_p1被复制到Qn2（ID_n2）的漏极电流。随后，运行返回至步骤3。 最终，Qn2的漏极电压（VD_n2）从初始电压开始升高。

增加的VD_n2被转移至后续的共源放大器。

共源放大器的VGS_n3升高，导致ID_n3增大。但ID_n3的增大受到电流源的Qp4的限制。由于VGS_n3的升高不会导致ID_n3增大，故Qn3的漏源电压（VDS_n3）降低。

这意味着当VIN(-)电压升高时，VOUT电压会降低。

使用运算放大器

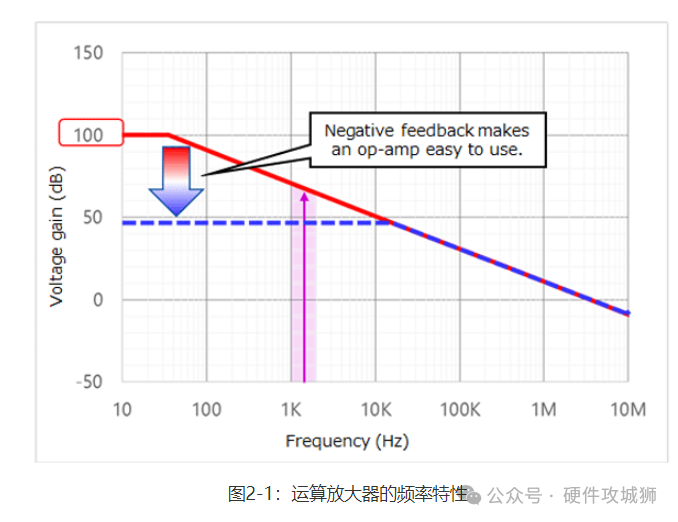
如图2-1所示，运算放大器具有高增益。增益取决于频率。增益也因器件而异，并受温度和其它环境条件的影响。因此，运算放大器通常与负反馈一起使用。根据条件，负反馈变为正反馈，导致反馈回路异常振荡。
第2节介绍了在考虑放大器电路时必需的反馈振荡、使用运算放大器的基本放大器电路、虚拟短路。 反馈（正反馈和负反馈） 开环增益和闭环增益 振荡 基本放大器电路 虚拟短路（虚拟接地）

2-1反馈（正反馈和负反馈） 运算放大器通常与负反馈联用。

本节简要介绍了负反馈。反馈环有两种类型：正反馈和负反馈。

例如，可将正反馈与以下循环进行比较： 1）你努力学习，成绩相应提高。

2）随着你的成绩提高，学习的乐趣增加，您学习更多。

3）你的成绩进一步提高。 换言之，正反馈是进一步增加输出端细微变化影响的一个过程。

相反，可将负反馈比作以下循环： 1）你努力学习，因此成绩相应提高。

2）你花更少的时间学习，而休闲娱乐时间增加。

3）你的成绩下降。

4）你的休闲娱乐时间变少，而学习时间增加。

5）您的成绩回到先前的水平。 这是试图使结果（即该示例中的成绩）保持不变的一个过程。此过程称为负反馈。 图2-2显示了一个带反馈的放大器电路，由一个放大器、一个反馈电路和一个加法器（或一个减法器）组成。其中，AV表示放大器的开环增益，B表示反馈系数。

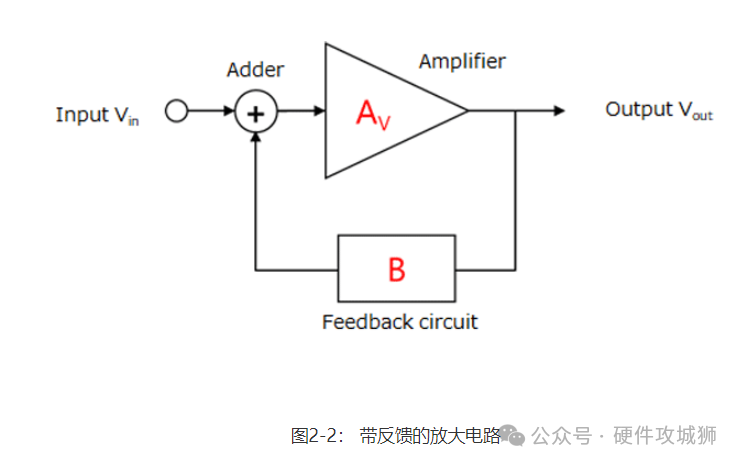
放大器放大输入信号并输出放大信号。部分输出通过反馈电路和加法器返回至放大器的输入端。

当Vin变化时，负反馈会改变放大器的输入，以抵消Vin变化的影响。相反，正反馈会增加Vin变化的影响。

输出（Vout）等于Vin和反馈信号之和乘以放大器的开环增益： Vout＝AV×（Vin＋B×Vout） 可将此公式改写为： Vout＝AV×Vin/（1－AV×B） 如果反馈信号（AV×B×Vout）与VIN信号同相，则放大器电路具有正反馈。如果反馈信号与VIN信号反相，则放大器电路具有负反馈。 正反馈：Vout＝AV×Vin/（1－|AV×B|）

负反馈：Vout＝AV×Vin/（1＋|AV×B|） 尽管运算放大器的开环增益非常高，但由于开环增益仍取决于频率，故难以使用此开环增益（详见第2.2节）。因此，运算放大器通常与负反馈一起使用。负反馈导致其增益大幅下降。另一方面，负反馈增加了使增益曲线保持平缓的频带宽度并减小了输出阻抗。此外，负反馈为创建易于操作的放大器创造了条件，因为它可以补偿增益变化。 正反馈通常不用于放大器。例如，正反馈用于为振荡器和比较器提供滞后性。（如果您对此感兴趣，详见常见问题（FAQ）：“如何实现比较器迟滞性（施密特触发器）？

2-2开环增益和闭环增益（增加放大器的带宽） 如图2-3所示，运算放大器的开环增益（GV）频率特性与一阶RC 低通滤波器的频率特性相同。在高于转角频率（即fC；在此频率下，开环增益比直流增益低3dB）的频率下，开环增益以每倍频程6dB（每十倍为20dB）的速率下降。在此频率范围内，当频率加倍时，运算放大器的分贝开环增益（GV）会减小6dB（即线性开环增益（AV）减半）。故： fc×AV＝常量 增益等于1（0dB）的频率称为单位增益交叉频率（fT）。因此，上述等式可重新表述为以下等式。这称为增益带宽积（简称为GBWP、GBW、GBP或GB）。 fc×AV＝fT 请注意，此等式在开环增益会以每倍频程6dB的速率下降的频率范围内成立。

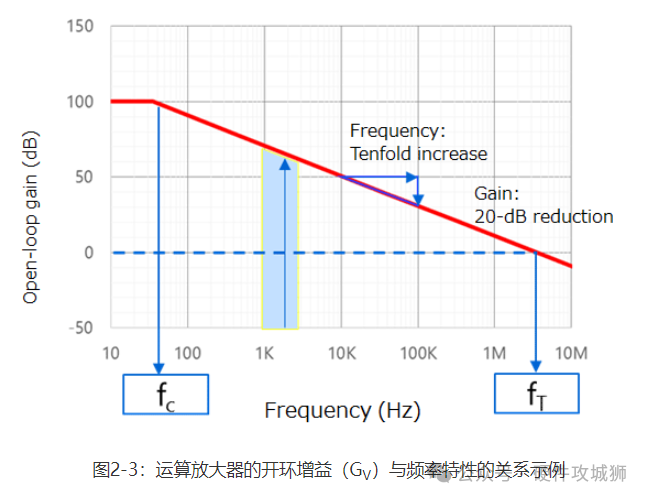
现在，我们来看下将频率为2±1kHz的输入信号施加于具有图2-3所示频率特性的运算放大器时会发生什么情况。这种条件下的运算放大器，3kHz的增益比1kHz的增益约低10dB。这种情况下通常不能使用运算放大器。负反馈解决了此问题。

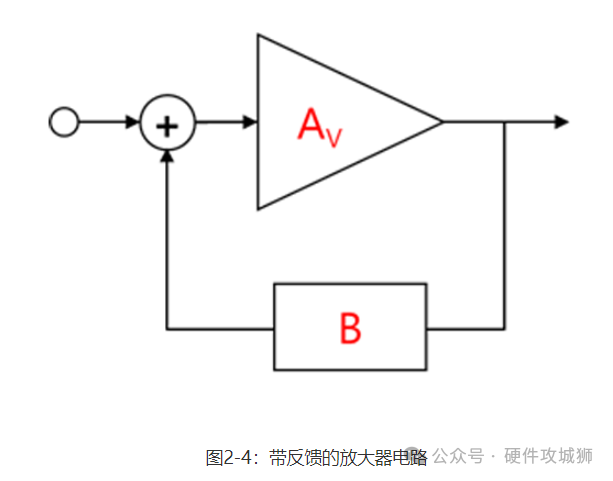
输入端（Vin）与输出端（Vout）具有以下关系。这种关系称为闭环增益（用dB标度表示为GCL，用线性标度表示为ACL）。20log规则用于将线性电压增益转换为分贝电压增益：G＝20×log A。 Vout/Vin＝ACL＝AV/（1＋AV×B）

　　　　　　    ＝1/{B（1 + 1/AV×B）} 其中，AV表示放大器的开环增益，B表示反馈系数。（AV×B）称为环路增益。分母（1＋AV×B）称为反馈量。在负反馈情况下，AV× B＜0。运算放大器的AV非常高。故|AV×B| >>1。因此，反馈量的计算公式为（1＋AV×B）≈AV×B（环路增益）。故可将上述等式简化为以下等式： Vout/Vin＝ACL＝1/B 图2-5显示了这种关系。运算放大器的带宽为fC。通过负反馈，其闭环带宽扩展至fCL。根据下列增益带宽积公式计算出fCL： fCL＝fT/ACL

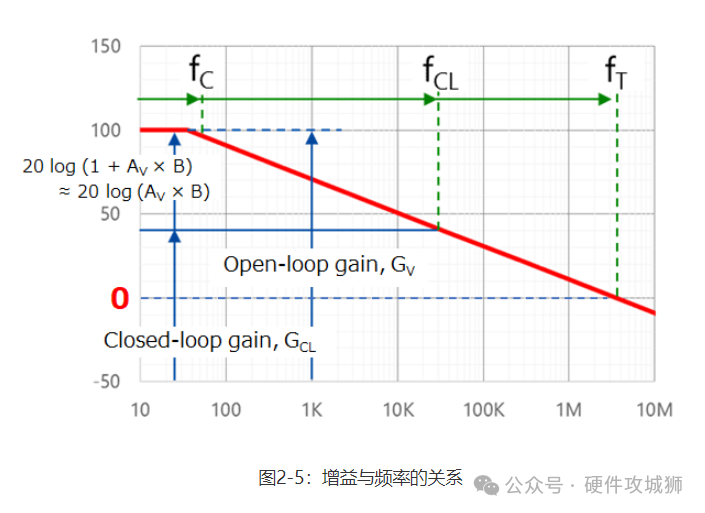
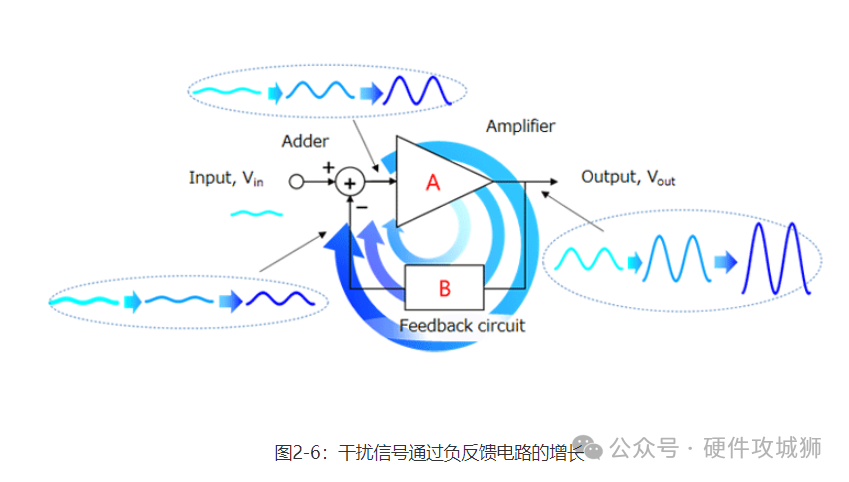
当闭环增益（GCL）或带宽（fCL）不足时，需选择fT较高的运算放大器。 2-3振荡 如图2-6所示，运算放大器通常与反馈电路一起使用。如第2.1节所述，反馈分为两类——正反馈和负反馈。当运算放大器用作放大器时，其被配置为负反馈。需注意反馈电路的振荡。

作为振荡来源的信号或噪声在某些条件下有可能发展为振荡。下面简要介绍振荡。

施加于输入端的振荡来源通过放大器和反馈电路。然后，加法器将其添加至Vin输入端。因此，加法器的输出会大于初始状态。随着此过程的重复，振荡来源增大，从而引发振荡。这就是正反馈的特性。

当您使用负反馈时，您可能认为振荡无关紧要。即使针对被放大的信号采用负反馈，其在较高频段也有可能变为正反馈。

设运算放大器的开环增益为AV，反馈系数为B，则反馈电路的传递函数表示如下。AV和B均为复数。 Vout＝AV/（1＋AV×B）×Vin 在负反馈电路情况下，AV×B＝＋|AV×B|。因此，如第2.1节所述，Vout提供稳定的输出。但由于所有电路都有延迟，故输出相位在高频时滞后于输入相位。

当输出相位滞后达到180度时，反馈电路变为正反馈回路。

如下图所示，输出的波形（Vout）会有所不同，取决于正反馈的环路增益（|AV×B|）的大小（即当来自反馈电路的信号与输入信号同相位时）。当振荡来源施加于输入端时，会发生阻尼振荡、持续振荡或爆发性振荡，具体取决于振荡来源频率下|AV×B|的大小。持续振荡通常称为振荡。由于开环增益（AV）受放大器动态范围的限制，因此爆发性振荡最终会减弱为持续振荡。  

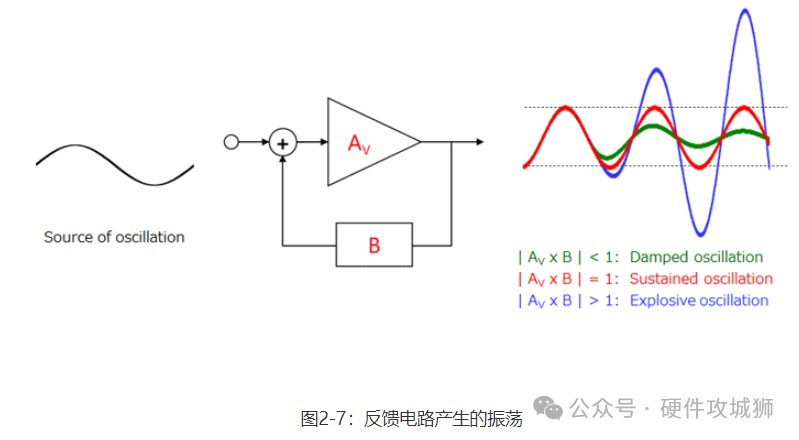
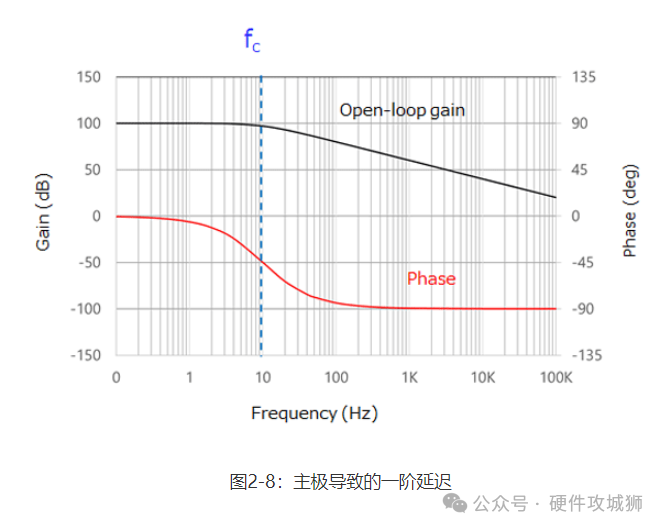
当环路增益（AV×B）满足以下条件（即传递函数的分母变为零）时，会发生持续振荡。此条件称为巴克豪森振荡条件（或简称为振荡条件）。 振幅条件：Re（AV×B）＝-1 相位条件：Im（AV×B）＝0 请注意，爆发性振荡最终会减弱为如上所述的持续振荡。因此，导致异常振荡的振幅条件如下： 振幅条件：Re（AV×B）＜-1 如图2-8所示，由于内部寄生电容，运算放大器具有一阶延迟元件（与一阶低通滤波器的情况一样）。

对于典型的运算放大器，开环增益响应的截止频率介于10Hz至100Hz之间。在此频率范围内，输出相位滞后45度。在开环增益以每倍频程6dB的速率减小的频率范围内，相位滞后为90度。
如果增益-频率关系曲线具有这种特性（只有一个主极点），则会在发生振荡前保留90度的余量。因此，不太可能发生振荡。  

运算放大器实际上有多个极点。图2-9所示的截止频率（fc）称为主极点。接近单位增益交叉频率（fT）的fc2处的频率极点称为第二极点。虽然较高频率下有更多极点，但他们不会产生任何实际问题。

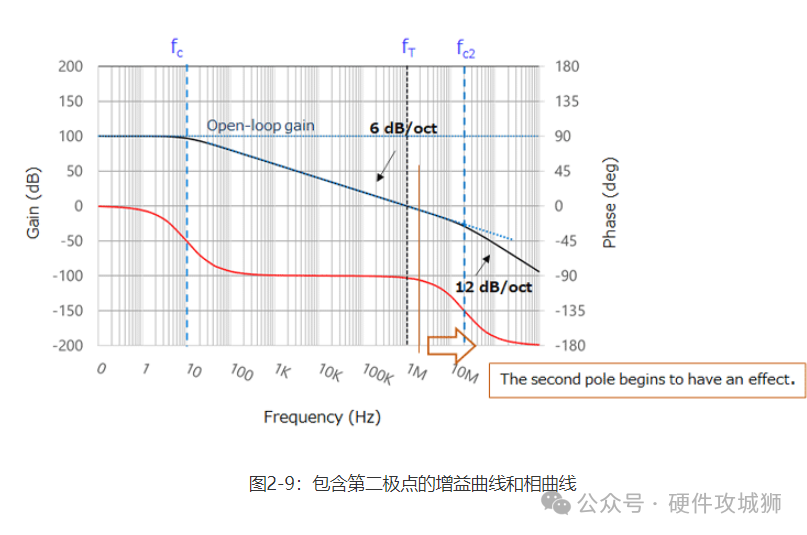
如图2-9所示，开环增益曲线的斜率在fc2处从每倍频程6dB变为每倍频程12dB。相位滞后也进一步增加了45度。当fc2高于单位增益交叉频率（fT）时，这种相位滞后不会导致任何问题。但即使fc2低于fT，在将运算放大器用作单位增益放大器（例如，电压跟随器）时仍应小心谨慎。（如果运算放大器的数据表显示其可与单位增益联用，则在高于fT的频率下其具有第二极点。）

为避免异常振荡，应在开环增益以每倍频程6dB的速率减小的频率范围（fc至fc2）内使用运算放大器。但请注意，在接近fc2的频率下，运算放大器会受第二极点影响，从而导致功率损耗和相位延迟。为完全避免其影响，闭环带宽（fCL）应小于fc2的五分之一。 以上是对运算放大器本身振荡的介绍。

还必须确保外部电路也无振荡（例如，相位延迟）。

例如，这种考虑适用于由运算放大器驱动电容性负载的应用。如果电容性负载导致的截止频率在环路增益大于1的范围内，则会发生振荡。为防止振荡，需在电容器上串联一个电阻器。即使运算放大器未连接负载，仍应注意导线或其它电容。尽量缩短从运算放大器输出端至后续器件的导线长度以及反馈回路的导线长度。

2-4运算放大器的基本应用 按照最基本的形式，运算放大器用作同相放大器（图2-10）和反相放大器（图2-11）。如上一节所述，同相放大器和反相放大器都有负反馈（输出端连接至VIN(-)）。

闭环增益（ACL）如下图所示。可使用下一节中描述的虚拟短路（亦称为虚短、虚拟接地或虚短路）概念轻松计算出增益。
同相放大器的输入阻抗非常高，因为其输入端直接连接至运算放大器。相反，反相放大器的输入阻抗低于同相放大器的输入阻抗，因为VIN(-)和VIN(+)具有相同的电位，因为他们实际上为虚拟短路状态并且R1作为输入阻抗。

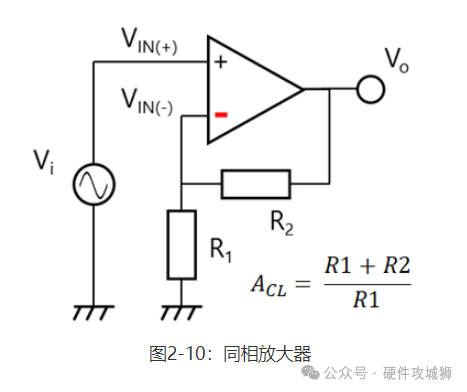
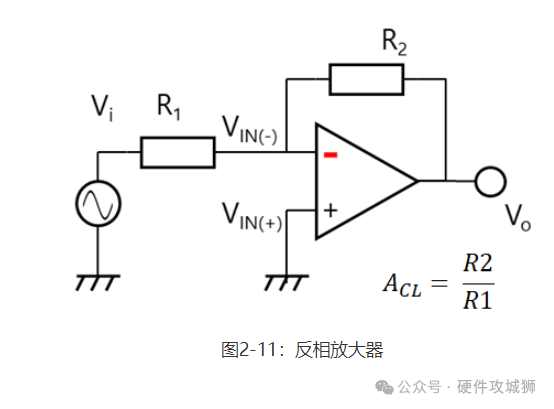
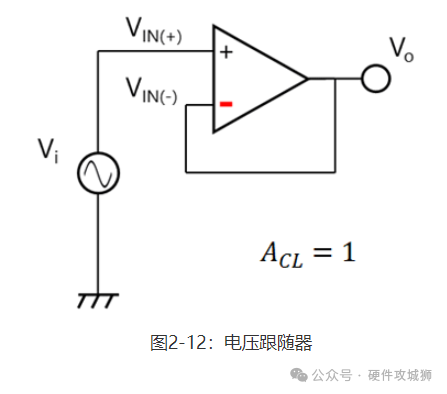
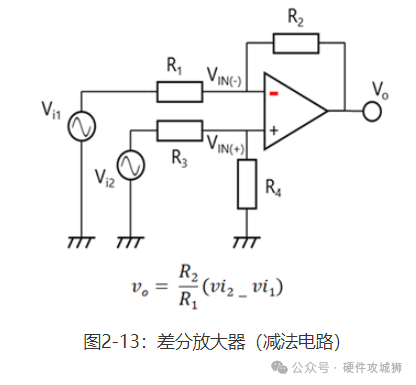
图2-12显示了一个电压跟随器。可将电压跟随器视为一个具有无穷大电阻R1且R2为零的同相放大器。由于电压跟随器的增益较低（单位增益，AV＝1），因此其带宽较宽。因此必须要小心，因为电压跟随器容易受第2.3节“振荡”中介绍的第二极点影响。大多数运算放大器可用作单位增益放大器，因为其在充分大于单位增益交越频率（fT）的频率下具有第二极点。而导线或负载电容可能会使其发生振荡。如果给定运算放大器的数据表显示其可在单位增益下使用，则其可用作电压跟随器。如欲将任何其它运算放大器用作电压跟随器，请联系东芝的销售代表。 此外，运算放大器具有多种应用，包括差分放大器（减法电路）以及加法器和积分器电路。  

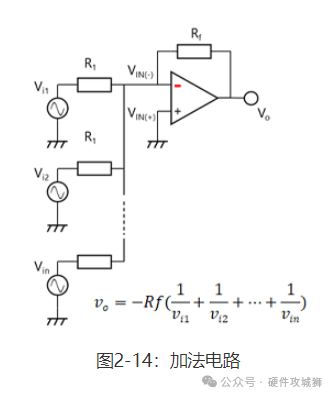
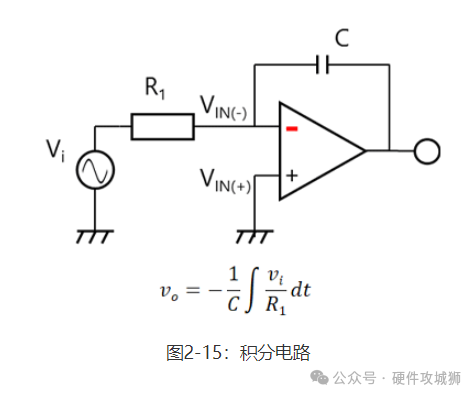
2-5虚拟短路（虚拟接地） 使用虚拟短路（亦称为虚拟短路或虚拟接地*）的概念可轻松计算出具有负反馈的运算放大器的闭环增益。

虚拟短路概念是指当具有较大开环增益时，无论输入信号如何，具有负反馈的运算放大器的VIN (+)端子和VIN (-)端子其电位几乎相同。 请考虑以下事项，直观地理解虚拟短路。

运算放大器将VIN(+)和VIN(-)之间的电压差放大100,000倍或以上（称为开环增益）。但真正的运算放大器的输出是有限的。因此，当使用运算放大器的放大器获得无失真输出时，VIN(+)输入端与VIN(-)输入端之间的电压差应能忽略不计。

在图2-16所示的负反馈放大器（反相放大器）情况下，由于输出端与输入端之间的连接方式，输出增加导致输入减少。因此，输出信号介于电源和接地端之间。（例如，假设一个反相放大器的输入电压为1 此时，运算放大器以100,000的开环增益运行。由于输出电压为3Vpp，故输入电压为3Vpp/100,000＝30μVpp。因此，VIN(-) ≈ VIN(+)。

接下来，我们通过简单计算来理解这一点。图2-16显示了使用运算放大器的负反馈放大器（反相放大器）。  

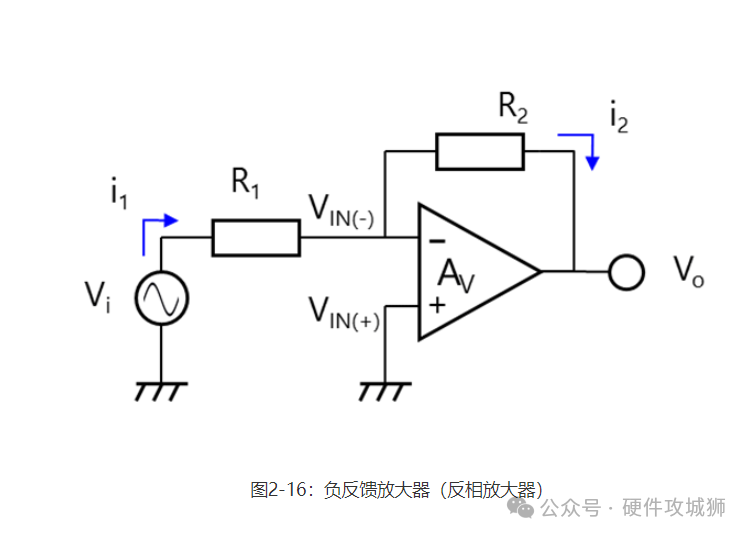
假设运算放大器为理想放大器。则会出现以下情况： 无穷大开环增益（AV） 无穷大输入阻抗 零输出阻抗 由于输入阻抗无穷大，流经R1的所有电流（i1）都流经R2。 i1＝（Vi – VIN(−)）/R1＝（VIN(−)－Vo)/R2          （1） 由下式得出运算放大器的输出电压：Vo ＝AV×（VIN(+) – VIN(−)）（2）

根据等式1和等式2，VIN(+)计算如下：

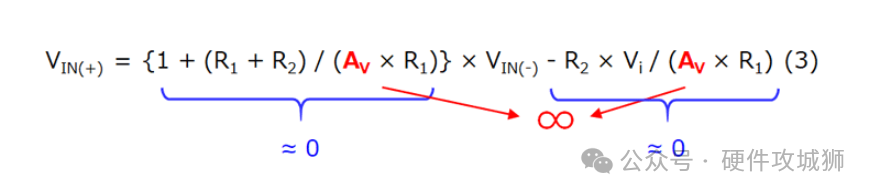
于输出阻抗为零，我们通过公式3得到VIN(＋)＝VIN(−)。

因此，VIN(−)输入端的电压等于连接至GND的V IN(＋)输入端的电压。

在这种情况下，VIN(−)输入端的状况即称为虚拟短路。 *广义上看，虚拟接地是电路的一个节点，该节点保持在一个稳定的基准电位，不直接连接至电源或接地。在图2-16的电路中，VIN(-)称为虚拟接地，因为其实际上等于GND。 接下来，让我们使用虚拟短路和理想运算放大器计算图2-17中所示的同相放大器的闭环增益（AV）。我们将输出电压（Vo）表示为Vi的函数。根据虚拟短路概念，VIN(-)＝VIN(+)＝Vi。 因此，流经R1的电流（i1）计算如下： I1＝VIN(-)/R1＝Vi / R1  

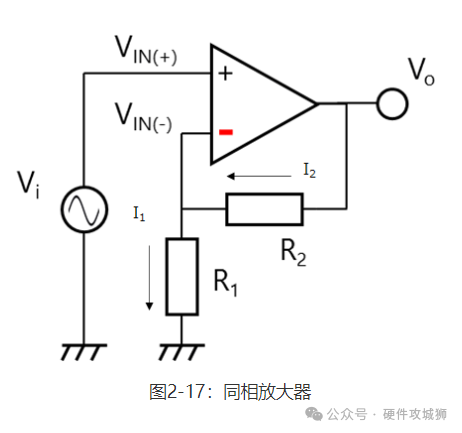
无电流流向运算放大器输入端，因为其具有无穷大阻抗。设流经R2的电流为I2，I1＝I2。故R2两端的电压（VR2）为： VR2＝R2×I2＝R2×Vi/R1 故Vo计算如下： Vo＝VR1＋VR2

＝Vi＋R2×Vi /R1＝Vi×（R1＋R2）/R1 AV＝Vo/Vi ＝（R1＋R2）/R1 您可轻松得到闭环增益等式。  

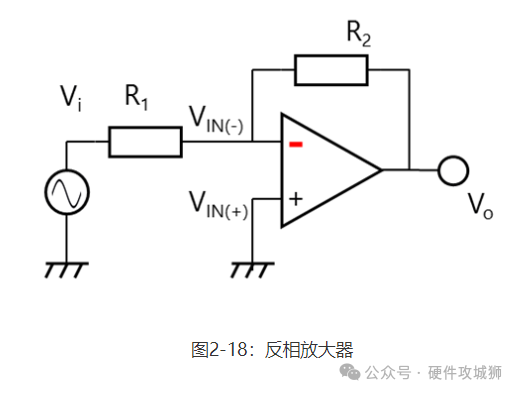
也可用相同方式计算出图2-18所示的反相放大器的闭环增益（AV）。 VIN(-)＝VIN(+)＝0V（GND）

I1＝V1/R1＝I2

Vo＝VR2＝R2×I2＝R2×V1/R1 故闭环增益为： AV＝Vo/Vi＝R2/R1  

电气特性

当运算放大器用作放大器时，共模输入电压范围表示其正常运行时的输入电压范围。当运算放大器用于放大来自传感器或其它器件的微小信号时，传感器分辨率对传感器的作用相当于输入补偿电压或共模输入信号抑制比（CMRR）对运算放大器产生的影响。最小分辨率取决于噪声量。

 

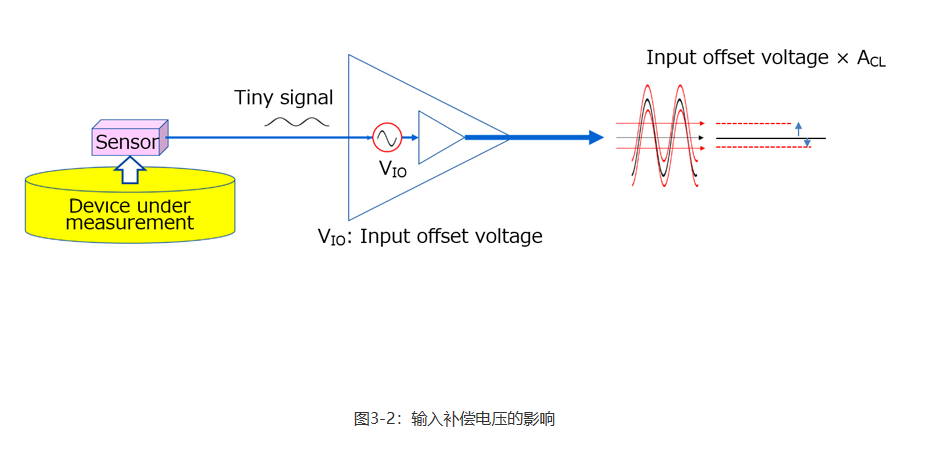
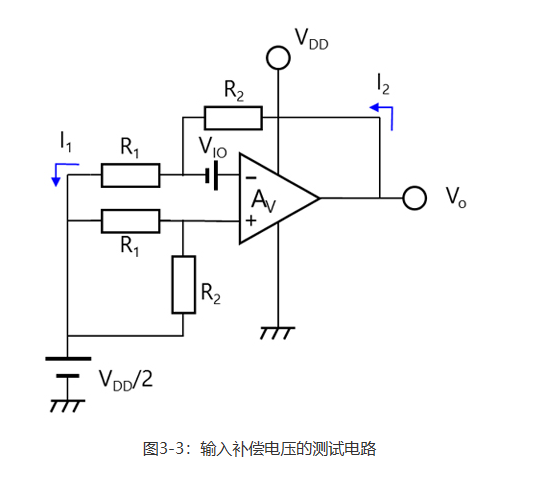
3-1输入补偿电压（VIO） 图3-3显示了无补偿电压源（VIO）的理想运算放大器。当共模输入电压同时施加于VIN(+)和VIN(-)时，输出（Vo）电压理论上变为VDD/2。但实际上其与VDD/2之间有一个小误差。输入补偿电压（VIO）是在VIN(+)与VIN(-)之间施加的将Vo误差降至零所需的电压。输入补偿电压的定义类似于下一节详细介绍的共模输入信号抑制比（CMRR）的定义。

在实际应用中，输入补偿电压乘以闭环增益（ACL）后会被加入输出电压中。因此，在传感器电路情况下，最大输入补偿电压必须低于其最小灵敏度。 我们来看下输入补偿电压为VIO的运算放大器。如图3-3所示的输入补偿电压测试电路显示，可将该运算放大器视为理想的运算放大器，外部VIo电压源连接至VIN(-)。

VIN(＋)电压变为VDD/2。根据虚短概念，VIN(-)电压也变为VDD/2。

因此，R1与R2交叉处的电压变为VDD/2－VIO。在理想运算放大器情况下，I1＝I2。 I1＝（VDD/2－VIO－VDD/2）/R1＝- VIO/R1＝I2
VO＝VDD/2－VIO＋（–VIO/R1）×R2

＝VDD/2－VIO×（R1＋R2）/R2 可将此公式改写为下列等式，以计算VIO： VIO＝（VDD/2－VO）×R1/（R1＋R2） 请注意，电阻器有一定的容限。实际测量时应使用实测电阻值。

VIO是VIN(-)与VIN(+)之间的差分电压。因此，当运算放大器与闭环联用时，将此输入补偿电压（VIO）乘以闭环增益后得到的电压将被添加到理想输出电压中。由于VO电压因器件而异，故在创建电路设计时需考虑最大补偿电压。如果超出系统的容限，则需修改电路结构以减少输入补偿电压的影响或选用输入补偿电压较低的运算放大器。  

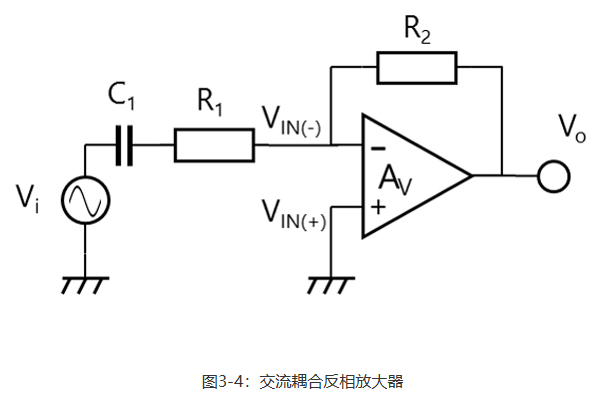
交流耦合电路是能降低输入补偿电压影响的最简单的电路形式。图3-4显示了一个交流耦合反相放大器。当电容器C1以这种方式连接时，由于输入补偿电压引起的电流不会流经R1。因此，输入补偿电压的直流增益为1，因此对VO的影响较小。

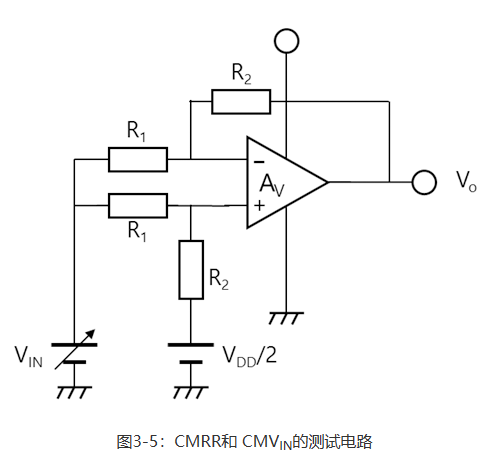
3-2共模输入电压范围（CMVIN）和共模输入信号抑制比（CMRR） 差分放大器的共模输入信号抑制比（CMRR）是一个指标，用于表示其抑制在VIN(-)端和VIN(+)端处具有相同振幅和相位的两个信号或噪声（共模噪声）的能力。用以下等式表示。共模输入信号抑制比的测试电路如图3-5所示。

共模输入电压范围（CMVIN）是指在规定条件下满足规定CMRR的输入电压多范围。东芝的运算放大器数据表中列明了直流条件下的CMRR值。

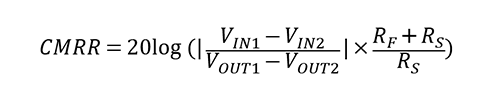
其中，VIN1和VIN2分别表示CMVIN的最大值和最小值，VOUT1和VOUT2分别表示VIN1端和VIN2端的输出（VO）电压。

从图3-5可以看出，上一节介绍的输入补偿电压（VIO）是特殊条件（VIN＝VDD/2）下的CMRR值。

运算放大器的运行方式如第1.2节所述。如图3-6所示，典型运算放大器的差分输入对由P沟道MOSFET组成。随着VIN(+)电压和VIN(-)电压的升高，电流源中Qp3的漏源电压不断降低，导致流向差分输入对和电流镜的电流略微减小。图3-7显示了分立P沟道MOSFET的一个ID-VDS曲线示例。例如，假设最初VDS＝ -1.5V且ID＝80mA。随着MOSFET的漏极电流减小，其漏源电压在饱和区呈非线性变化。

尽管运算放大器IC的内部器件的放置和制造方式保证了MOSFET的均匀性，但其在微观层面并不完全对称。此外，半导体芯片先贴装在封装的金属框架上，再焊接至印刷电路板。因此，施加于运算放大器IC的每个元件上的机械应力略有不同。这些因素导致差分输入对的P沟道MOSFET之间的阈值电压略有不同。因此，漏极电流的减小会导致其漏源电压发生不同的非线性变化。因此，如图3-8所示，输入补偿电压在共模输入电压范围内相对于输入电压（VIN）有一个斜率。因此，CMRR值是在最大和最小共模输入电压下计算得出的。

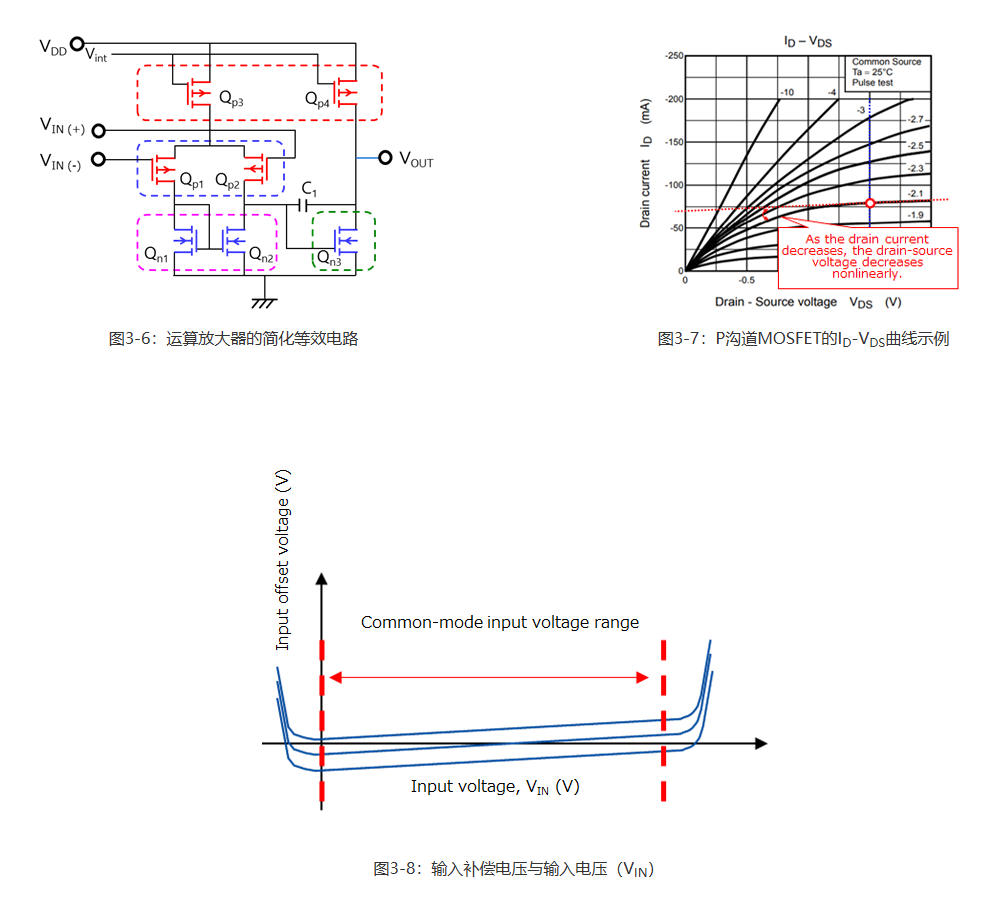
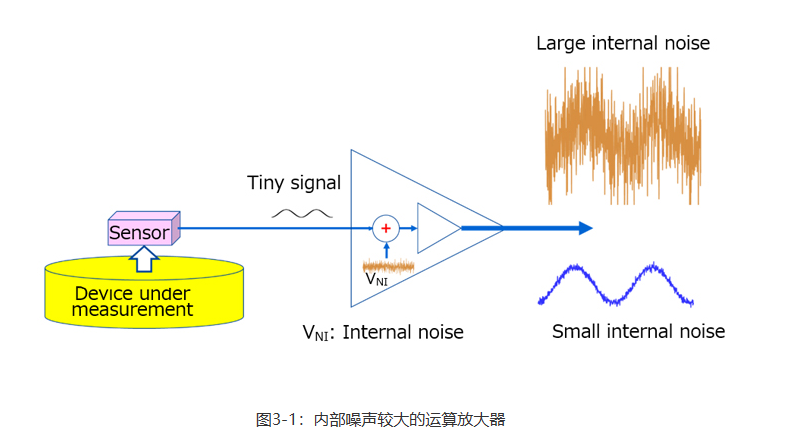
3-3运算放大器的内部噪声 运算放大器用于放大来自传感器或其它器件的微小信号。噪声加至这个微小信号中，并被运算放大器放大。因此，噪声会降低传感器的灵敏度和精度。

与运算放大器相关的噪声分为由电磁干扰和外部器件导致的外部噪声以及内部噪声。本节重点介绍运算放大器的内部噪声。 将两种内部噪声定义为等效输入噪声： 取决于频率的1/f噪声：电阻器产生的热噪声以及半导体中自由移动的载流子产生的散粒噪声 与频率无关的白噪声：由晶体缺陷导致的闪烁噪声以及突发噪声 图3-9显示了运算放大器的噪声频率特性，图3-10显示了一个实测等效输入噪声电压示例。图3-10比较了东芝的TC75S51通用运算放大器和TC75S67低噪声运算放大器。

通用运算放大器的白噪声约为30nV/√Hz，转角频率为300Hz，而低噪声运算放大器的白噪声约为6nV/√Hz，转角频率为100Hz。  

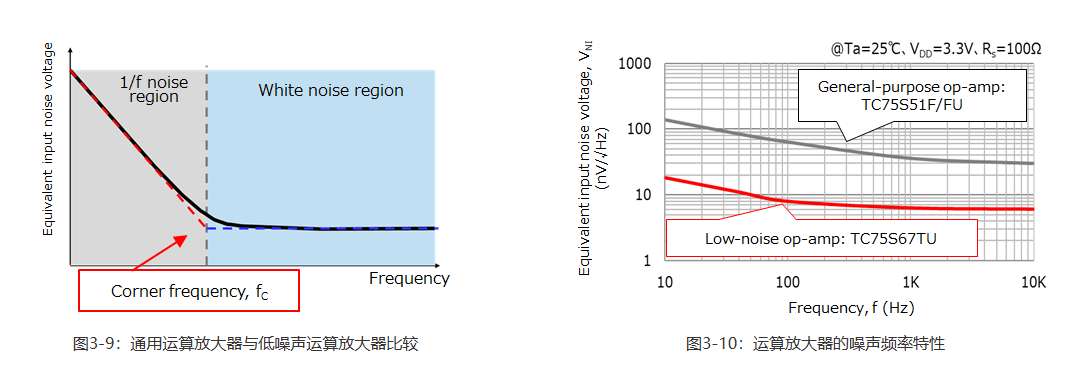
1/f噪声和白噪声均出现在运算放大器的输入端，并且都被定义为等效输入噪声电压。等效输入噪声被增益放大并出现在输出端。需特别注意低频噪声，因为它的电压取决于频率。 为放大微小信号，有时会级联多个放大器以防止异常振荡。我们来看下每个放大器级如何影响出现在级联放大器输出端的噪声。

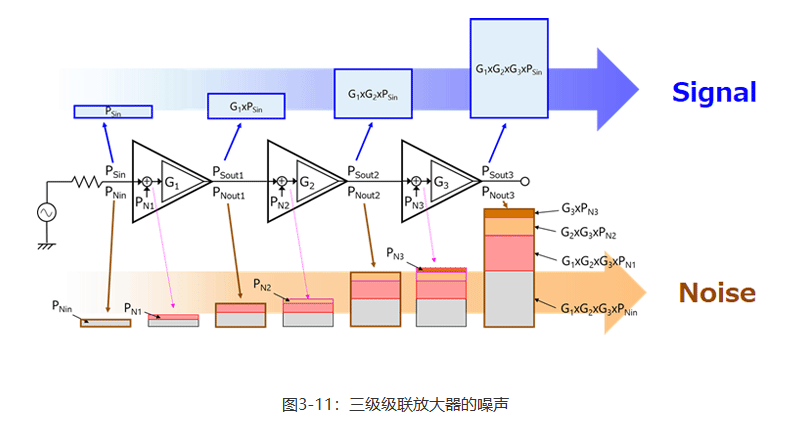
图3-11显示了一个三级级联放大器。

如图3-11所示，可按下式计算输出信号功率（PSout3）和输出噪声功率（PNout3）。

如您所见，第一级放大器的输入噪声（PNin）和等效输入噪声（PN1）对输出噪声的影响最大。 用以下等式表示输出信号功率（PSout3）和输出噪声功率（PNout3）： PSout3＝G1×G2×G3×PSin
PNout3＝G1×G2×G3×（PNin+PN1）＋G2×G3×PN2＋G3×PN3 因此，可按下式计算噪声系数（F，这是一个噪声的度量）：

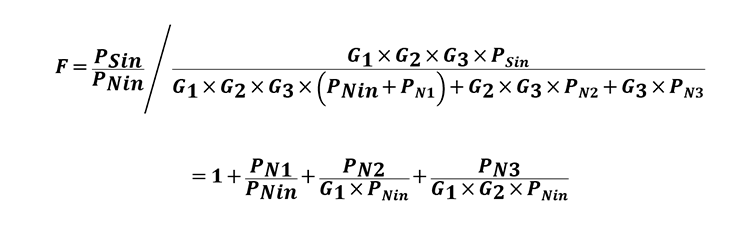
第二级放大器的等效输入噪声（PN2）除以第一级增益（G1），而第三级放大器的等效输入噪声（PN3）除以第一级增益和第二级增益（G1和G2）。因此，各放大器连续级的输入噪声对输出PNout3的影响逐渐降低。如本例所示，应在第一级使用低噪声放大器以减少其噪声的影响。

3-4噪声增益和信号增益 上一节介绍了运算放大器产生的不同类型的噪声。如前所述，运算放大器的内部噪声是指等效输入噪声电压。图3-12显示了一个简化等效电路。三角形代表的运算放大器为理想的运算放大器。由于图3-12中将等效输入噪声电压（VNI）表示为VIN(+)与VIN(-)之间的一个电压差，故VNI与VIN(+)或VIN(-)是否串联插入无关紧要。

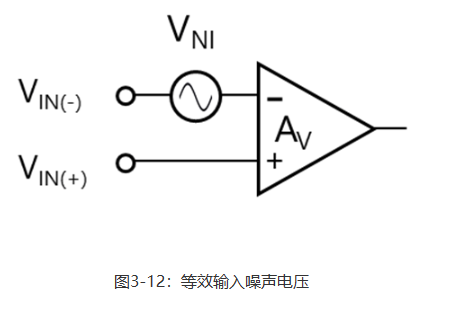
接下来，我们来看下使用此模型的同相放大器和反相放大器。

图3-13显示了一个反相放大器，图3-14显示了一个同相放大器。反相放大器和同相放大器都有一个等效输入噪声源（VNI），其与理想运算放大器的Vin(-)输入端串联。如第2.4节和第2.5节所述，这些放大器的信号增益为AV。

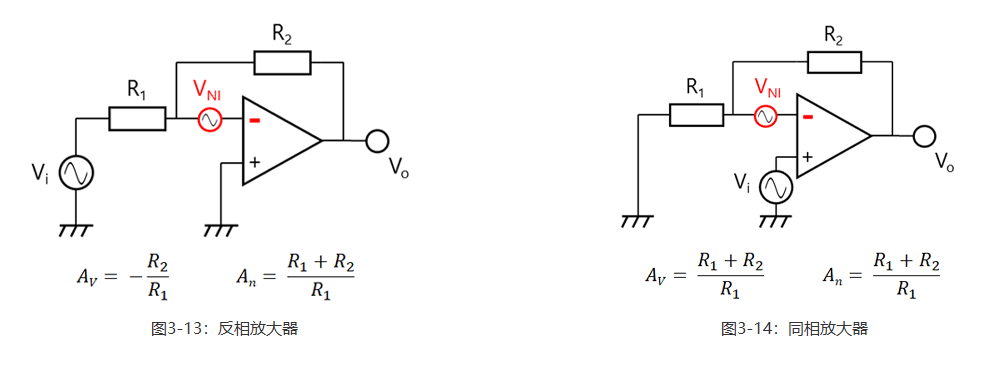
利用叠加原理，可分别考虑信号源和噪声源。让我们计算噪声源的增益。此时，根据叠加原理，Vi被视为短路。
由于VIN(+)输入端在图3-13中已接地，故VIN(-)输入端也可视为接地。因此，R1和R2交叉处的电位变为VNI。

由于流经R1的电流（I1）不会流向运算放大器，所有I1全部流经R2。 I1＝VNI/R1 因此， VO端的噪声电压（VNO）计算如下： VNO＝VNI＋R2×VNI/R1＝VNI×（1＋R2/R1） 由于噪声增益（AN）等于VNO/VNI， AN＝1＋R2/R1 由此，运算放大器中产生的噪声增益可能不同于信号增益。此增益称为噪声增益。 可以如下方式使用噪声增益的概念： 将等效输入噪声转换为输出噪声 计算输入补偿电压对输出的影响 计算振荡余量 如上所述，噪声增益的概念对于使用运算放大器的电路很重要。 接下来，下文简要介绍了振荡余量。

除振荡器外，振荡是指信号在非预期频率上发生的意外波动。如第2.3节所述，意外噪声等振荡来源通过反馈回路进行循环，逐渐演变为振荡。

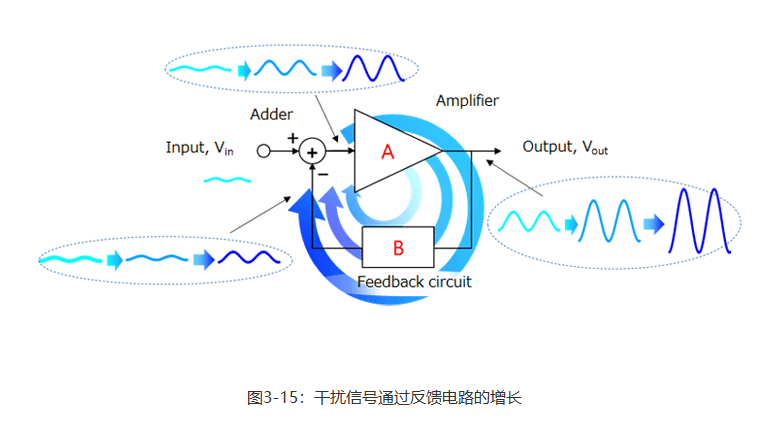
振荡来源为随机噪声。其用作运算放大器的VIN(+)输入端与VIN(-)输入端之间的电压差。换言之，其为前文介绍的等效输入噪声电压（VNI）。

必须根据噪声增益确定振荡抗扰度，这一点很重要。如上所述，典型的反相放大器和同相放大器的噪声增益可使用同相放大器的信号增益等式进行计算。

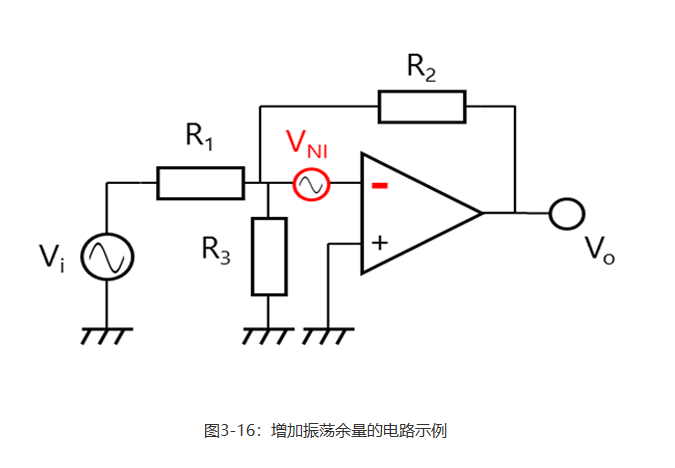
噪声增益的概念可用于为振荡提供余量（即增加噪声增益）。 图3-16显示了使用反相放大器在不改变信号增益的情况下增加振荡余量的一个示例。

现在我们利用叠加原理分别考虑Vi和VNI。

（当考虑Vi时，VNI被视为短路；当考虑VNI时，Vi被视为短路。） 根据虚短概念，VIN(-)输入端和VIN(+)输入端均视为已接地。

因此，由于在信号增益为AV（= Vo/Vi）时R3两端的电压等于GND电位，故没有电流流经R3。因此，AV = -R2/R1，这与基本反相放大器的等式相同。

由于Vi在噪声增益为AN（= Vo/VNI）时短路，故Vi = R1 // R3。因此，AN = 1 + R2 / (R1 // R3)，高于基本反相放大器的噪声增益AN = 1 + R2 / R1。这意味着此电路提供了比基本反相放大器更大的振荡余量。

但由于噪声增益的概念与输入补偿电压的概念完全相同，振荡余量增加也会导致输入补偿电压相应升高。  

审核编辑：黄飞