一文解析HA5WH相位移位网络(phase shift network)

在SSB单边带调制中，会用到RC-多相网络，这个网络非常有意思，在空间中是一个圆柱形，并不能用平面表示。这篇文章对RC-多相网络原理进行了分析和理论推导。这里介绍给感兴趣的同学。

本文分析了HA5WH相位移位网络(phase shift network)。描述了具有循环对称性的理想网络，并提供了简单的设计方程。通过考虑元件容差进行的计算表明，必须使用匹配良好的元件才能获得高质量的结果。

目录

1. 引言

单边带信号的产生或检测的移相法需要在音频频率范围内具有的相对相差的两个信号。移相法一直不太受欢迎，特别是在相对便宜的滤波器出现之后。未来，数字信号处理技术大概率将执行必要的音频相位移或直接生成射频单边带信号。那么，为什么你还对音频相移网络感兴趣呢？或许是因为它们较低的成本、易于构建，并且非常有趣。此外，笔者在这里描述的技术对于其他级联网络的有效分析也是非常有用的。

多年来，ARRL手册[1]中包括了一个由HA5WH设计的音频相移网络电路。笔者还没有找到这个网络的原始参考文献。手册声称，该电路使用的公差元件，可以提供大约的边带抑制。这与通常的结果相悖，即你需要的元件来获得约的抑制。在本文中，笔者将分析这类网络并给出设计方程。不幸的是，这种分析表明，使用公差元件可能导致边带抑制不良。使用理想元件，网络可以提供优异的性能，通过使用高公差元件或匹配良好的低公差元件，网络仍然可以提供良好的性能。

在第2节中，笔者给出了边带抑制的一般公式，用相位和幅度误差表示相位网络中的边带抑制。在第3节中，笔者推导了一种有效的分析一般HA5WH型网络的方法。第4节给出了对网络理想实现的分析。第5节描述了用易于计算的椭圆函数对网络进行优化，第6节给出了元件公差的影响。结果是一组简单的设计方程，用于理想网络，并估计了对元件公差的敏感性。附录中列出了一组实现所述方法的Fortran程序。

2. 相位误差对边带抑制的影响

移相法生成的单边带信号在数学上表示为，其中正负号分别表示上（下）边带，，是载波频率。类似地，，是音频调制频率。余弦函数可以写成

这是移相法的基本方程。右侧的乘法是通过平衡调制器完成的，而且两个音频信号（以及两个射频信号）相位差必须为，且幅度相等。我们假设射频信号恰好相位差为，且幅度相等。使用常规的复数表示法，其中表示一个音频信号，表示另一个音频信号，使用非理想的相移网络的结果为

边带抑制（或增强）由下式给出：

注意，如果等于，即两个信号的幅度相等，那么对于相位误差，抑制（以分贝表示）简单表示为：

3. 分析HA5WH网络

图1给出了ARRL手册中的HA5WH网络的电路图。有了这个电路，可以使用网孔或节点分析轻松地进行数值分析。这种暴力方法的缺点是它无法解释网络为何有效，或者网络的变化如何影响其性能。因此，笔者将提出一种方法，这种方法在数值上更有效，而且通过使用理想网络的对称性，可以得出简单的设计方程。

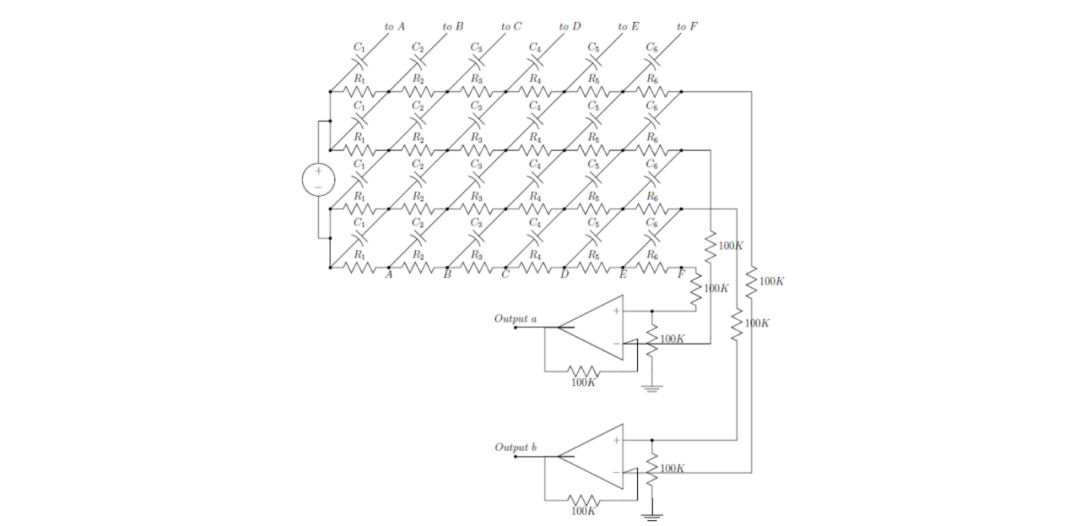
图1：HA5WH宽带相移网络的示意图。

显然，该移相网络由6个相似的部分组成，每个部分都有4个输入连接和4个输出连接。其中一部分如图2所示。

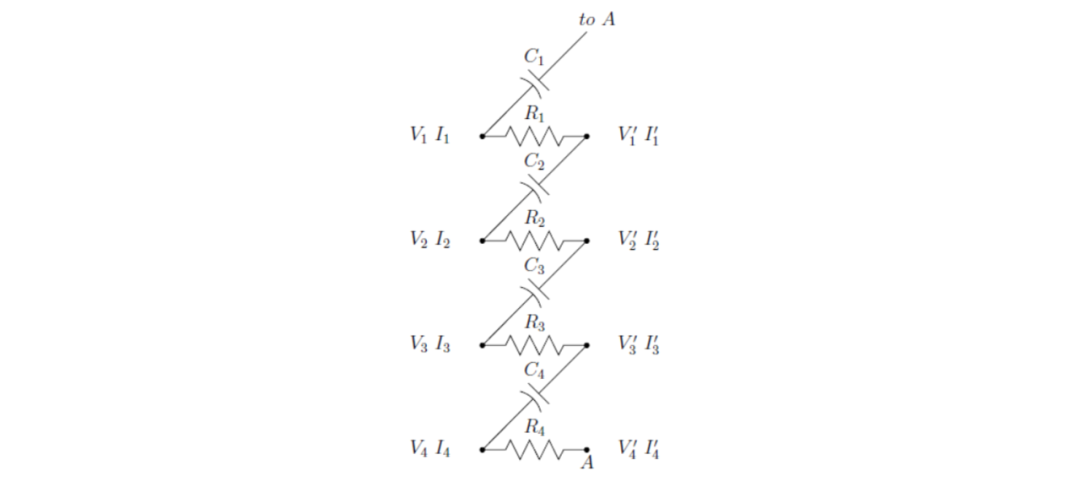
图2：HA5WH网络的一部分的示意图。

将输入电压和电流标记为。相应的输出电压和电流标记为。对这个网络直接进行节点分析，得到了由矩阵方程表示的8个线性方程：

其中是长度为4的向量，是4×4矩阵。式5紧凑地表示了网络各节点处的电流守恒要求的8个方程。矩阵如下：

与使用矩阵级联二端口网络完全类似，为了级联这些网络部分，定义一个新的矩阵方程，解出矩阵得到，其中是矩阵的逆。

将网络的每个部分的8x8矩阵标记为，将输入与整个网络输出相关的矩阵是，由四个4x4矩阵组成，表示如下：其中是矩阵乘积。

手册中的电路在4个输出连接上4个负载电阻。将它们标记为，并定义一个的负载矩阵，

可以将输出电压和电流之间的关系写为，

解出，然后进行反向代入，得到最终的网络矩阵方程，它将4个输出电压与4个输入电压相关联，

式中，式15中的1代表单位矩阵，

如果输出电阻相对于其他电路阻抗来说很大，可以被视为零。在这种情况下，方程简化为，

手册中的网络使与下式成正比，

在从电路数值计算得到和矩阵之后，输出信号需要按以下方式组合，

边带抑制由式3给出。信号的相对幅度和相位也可以被计算出来。大多数相移网络都是基于全通网络的(all pass networks)，因此所有信号的幅度都具有相同的衰减。但HA5WH网络不是全通网络。理想情况下，我们希望既有很好的边带抑制，又希望和在音频电路的通带范围内保持恒定的幅度和相位。

如果被求逆的矩阵变为奇异矩阵，上述分析将在奇异点失效。例如，当在

在这些点附近，计算中的舍入误差会很大。对于这里的分析，不是一个大问题。然而，在具有许多部分或接近奇异点的网络上进行分析时，将需要采用的更多的数值计算技巧，或者使用标准公式，在该公式中一次性求解完整的网络方程组。

4. 理想循环网络的分析

如手册所示，HA5WH网络的设计在每个网络的六个部分中都包括四个相同的电阻和四个相同的电容。这意味着该网络在其端口顺序的循环交换下是不变的。也就是说，如果我们通过将1变成2，2变成3，3变成4，4变成1来重新标记端口，我们将得到描述网络的完全相同的方程。这种不变性通常使用群论的数学方法处理[2]，这极大地简化了对具有对称性系统的研究。理想的HA5WH网络具有所谓的循环4或对称性。可以使用群论来分析网络方程。对代表循环运算符的矩阵特征的分析表明，的4个不可约表示各出现一次。因此，它们对应于矩阵的4个特征向量，可以立即写出这些向量。

然而，大多数无线电爱好者可能对群论不太熟悉，然而，可以在不使用群论的情况下轻松验证这些结果。矩阵的右特征向量和特征值由以下方程确定，

即将特征向量与矩阵相乘后，得到的结果仍然是该特征向量，只是乘以了特征值。将矩阵乘以其中一个特征向量的效果就是将该特征向量乘以特征值。在我们的基础上，循环特征向量是在元素之间具有恒定相位差的向量，且在最后一个元素与第一个元素之间的相位差也相同。这就有了以下关系，

通过直接的矩阵乘法，可以轻松验证如果在网络部分中所有的和值相同，这些向量就是所有矩阵的特征向量。这是循环4对称性的直接结果。此外，由于矩阵是矩阵的乘积的组合，这些相同的向量也是矩阵的特征向量。由于可以表示为矩阵乘以的组合，如果我们将表示为四个特征向量的线性组合，将通过取相同的线性组合并将每个项乘以适当的特征值得到。网络必须被设计为产生的相对相位差。

HA5WH网络的输入只包含上述的最后两个特征向量，即

最后一行定义了相关的特征向量为和。此外，如果输出阻抗相同并且运算放大器具有良好的共模抑制能力，输出对于前两个特征向量也不敏感。如果由于元件容差而破坏了循环对称性，同时满足这两个条件将是有帮助的。

当输入如式23所示时，输出通常会是

而平衡调制器的两个输出将是

边带抑制（以分贝表示）使用式3为

因此，为了设计一个好的网络，我们必须消除这最后的两个特征向量中的一个。到目前为止的分析显示了如何构建HA5WH网络。特征向量在4个电压上具有相等的幅度，并且在相邻端口之间有和的相位差，最后一个相当于的相位差。我们希望选择网络驱动、连接和元件值，以选择出两个相位差的特征向量中的一个。另外，同样的思想也可以用来设计一个相对相位差为的网络，只需使用在群下不变的网络，或者从群得到的相位差等。

选择元件值的第一步是计算四个矩阵的特征值。通过直接相乘，得到

其中上标a或b表示特征值对应于特征向量或。

当输入一个特征向量时，一个矩阵的作用是将式11中的矩阵替换为它们的特征值。经过一些代数运算，得到，

矩阵与成比例。如果我们向网络部分提供和的线性组合，该部分相对于抑制的因子为

HA5WH网络具有以下特性：在正频率下，式30中的比值的幅度始终小于1，而在时恰好为零。第一个特性表明，额外的网络部分只能改善输出的相对相位差。第二个特性表示，我们可以通过选择单个网络部分的值来设置精确相位差的频率。这两个特性极大地简化了网络的设计和优化。

单一频率下的边带抑制，对于一个包含个部分的网络，其中第i个部分的值分别为和，可以表示为

选择每个部分的值的简单方法是使用计算机绘制上述结果，并调整和以达到所需的抑制效果。实际上，如果你试图使用已经在你废品箱中的一组零件进行设计，这是一个显而易见的技术。然而，抑制效果的形式使得在下一节中看到的最佳值的选择变得容易。

5. 优化边带抑制

的最佳值可以使用椭圆函数轻松计算。通常，我们希望最坏情况下的抑制效果尽可能高。这引导我们使用等纹波或切比雪夫逼近。相关数学方法的细节可以在Saraga的著作[3]中找到。对于上限频率和下限频率，个部分网络的值为，

其中，表示第一类完整椭圆积分，是雅可比椭圆函数[4, 5]。

在表1中，给出了一些对业余爱好者来说可能感兴趣的网络的计算值，以及它们的理论边带抑制效果。这些理论结果当然是在假设元件完美的情况下得到的最佳情况。

顺便提一下，注意到Saraga的泰勒逼近[3]是通过简单地选择所有的值相等，并且等于得到的。此外，如果在特定频率（例如，如果您希望在单边带发射机中使用音频音调产生频率移键控）需要最大抑制效果，那么可以简单地选择适合这些频率的值，然后优化其他网络部分。

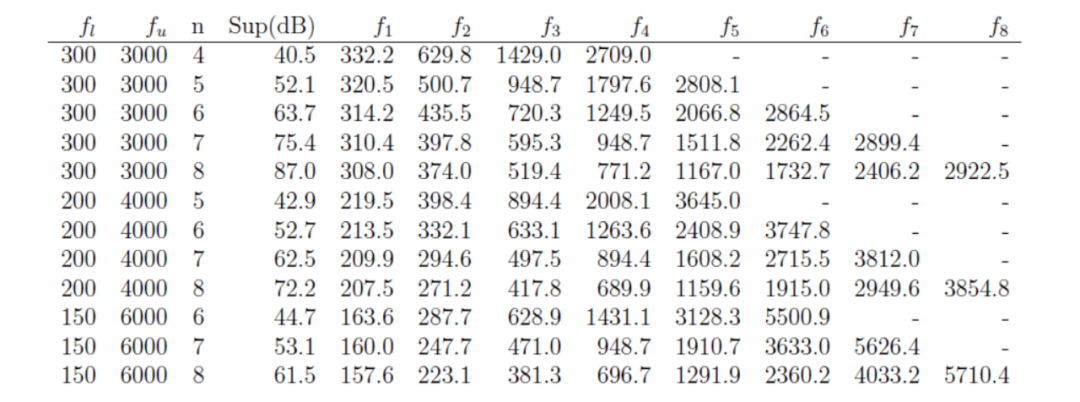
表1：一些理想的HA5WH类型相位网络的最佳切比雪夫值。和分别为上限和下限频率，是网络的阶数，，其中从1到，是精确相位差的频率。相应的值为。Sup表示网络范围内最小的边带抑制效果，以分贝表示。

6. 振幅变化和元件容差的影响

到目前为止，只关注了两个输出之间的相对相位差。为了获得高质量的音频信号，网络的输出必须是平坦的。通常，这可以通过构建全通网络来实现。由于HA5WH网络不是全通形式，我们必须研究其频率响应的衰减。在图3、4和5中，分别绘制了为频率范围为到设计的最佳4、6和8部分滤波器的边带抑制效果，一个输出信号的幅度和相位变化，这些滤波器使用相等阻值的电阻。网络的各个部分按照值从大到小的顺序排列，与原始的HA5WH设计一致。如图所示，幅度变化小于，相位变化平滑，边带抑制效果符合预期的等纹波形式。

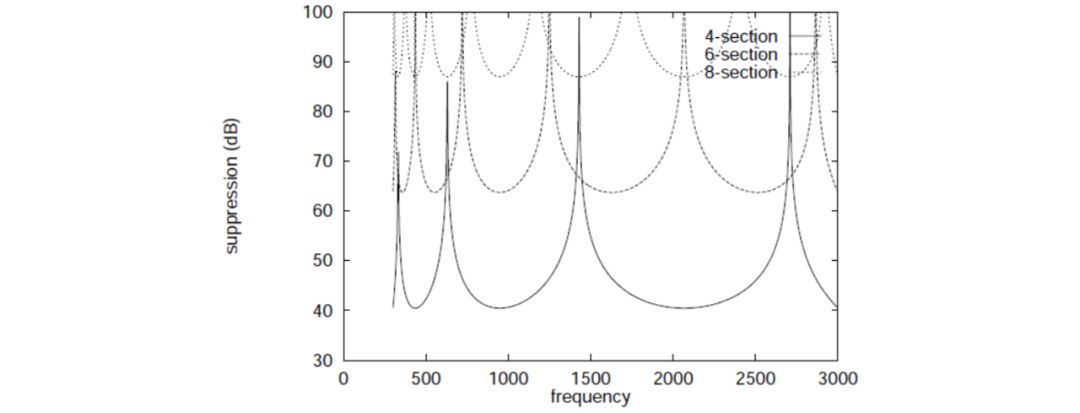
图3：在频率范围为到时，4、6和8个最佳切比雪夫网络的非期望与期望边带幅度的比率。

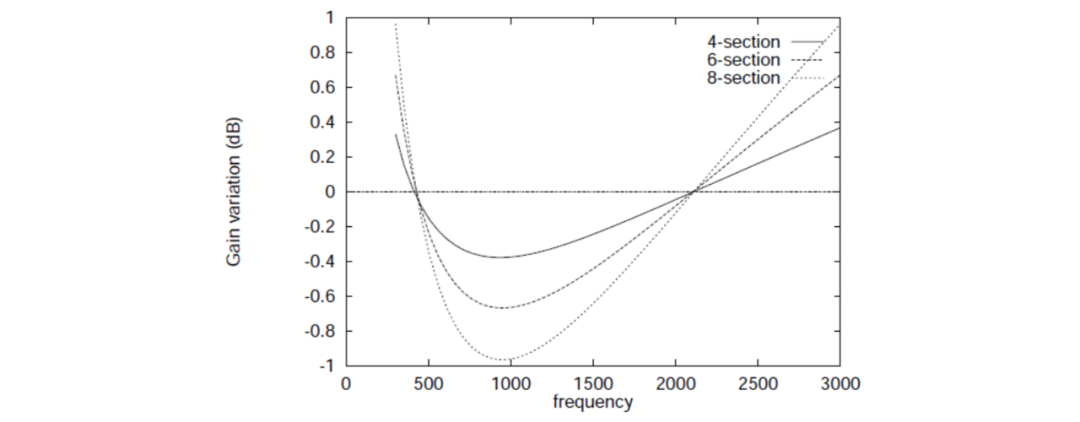
图4：在频率范围为到时，4、6和8个最佳切比雪夫网络的一个输出信号的相对幅度。

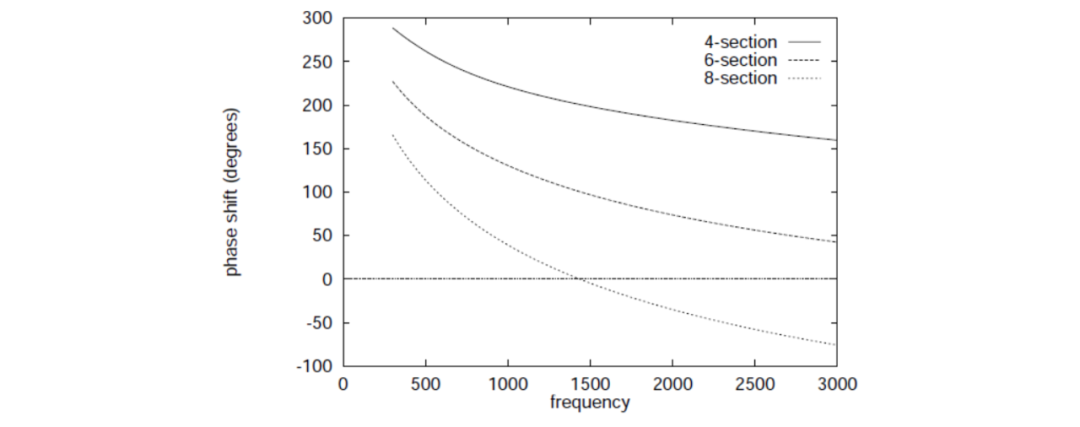
图5：在频率范围为到时，4、6和8个最佳切比雪夫网络的一个输出信号的相位差。

该网络在手册中的主要优势之一是声称可以使用低容差元件制造高性能网络。从第5节的分析中，如果保持循环对称性，网络将在每个网络部分对应的个选定频率（即）处完美运行。由于一般来说元件的匹配比准确测量它们的值更容易，笔者研究了由于完全匹配但容差较低的元件引起的这些节点频率变化的影响。由于电阻和电容都可能有变化，使用10%的元件可能会导致节点频率的变化约20%，如果两种元件的值都朝着同一个方向变化。最糟糕的情况是所有部分的频率都比正常值高或低20%。这只是将网络的中心频率向上或向下移动20%。对于在到范围内的最佳6部分滤波器而言，这将把边带抑制效果从超过降低到约。如果假设网络节点频率的变化为10%（即5%的元件），并且再次假定所有频率变化的方向相同，抑制效果接近。这表明相对低容差但匹配良好的元件可以获得出色的结果。当每个滤波器部分的元件是完全匹配的时，式31可以轻松用于预测由于元件容差导致的每个滤波器部分的值变化的影响。

当每个部分中使用不匹配的和值时，这当然是最具实际兴趣的情况。在这种情况下，我们可以通过观察当M矩阵不再是循环时，和之间的交叉项来了解最坏情况的可能性。典型的项给出了贡献，如下所示：

或

其中，这里的下标表示网络部分中的位置，如图2所示。这表明，一个具有表示容差)的单个部分可以将总体抑制效果降低到大约。也就是说，如果网络部分中的元件没有匹配，那么的元件可能导致抑制效果降低到，的元件可能降低到。请注意，为了确保获得60 的相对抑制效果，需要使用短期和长期容差为的元件。作为对不匹配元件敏感性的具体例子，笔者计算了原始HA5WH 6部分滤波器的抑制效果，其中只有最后一节的电阻被改变了。和提高了，和降低了。对于理想元件，抑制效果大于。只改变最后一节的电阻将抑制效果降低到，与上面的简单计算结果大致一致。利用这些结果尝试构造近似最坏情况的情形，笔者尝试以完全相同的方式改变每个部分中的所有电阻。此外，通过将和的值提高并将和的值降低来改变所有电容器的值。结果是进一步降低了不需要的边带抑制效果，降低到约。显然，10%的元件和运气不佳将产生不可接受的边带抑制效果。

7. 结论

HA5WH网络利用循环对称性提供了简单的设计方程，并且在理想元件下具有出色的边带抑制效果。如果保持循环对称性，网络对于元件公差不太敏感。这意味着每个网络部分的元件应该被精心匹配。通过使用不匹配的元件打破循环对称性可以严重影响网络的性能。

8. 勘误和附录

在发表本研究报告后，笔者受到了Gingell（KN4BS）的联系，他告诉笔者说他是这个电路的发明者，也是类似电路中称为“A Symmetrical Polyphase Network”的其他电路的发明者。他对笔者在这里提到的大多数结果都有所了解，除了Saraga的方法应用于形成Chebychev网络的部分可能例外。然而，他告诉笔者，Saraga是他的博士答辩委员之一，所以笔者认为Saraga的方法对他并不完全陌生。

以下是他发送给笔者的一些参考文献，其中包含了更多的历史背景。

　　1. M.J.Gingell： “A Symmetrical Polyphase Network” British Patents 1，174，709 and 1，174，710 filed 7th June 1968， published 17 Dec 1969， US Patents 3，559，042 and 3，618，133 published Jan 261971 2. M.J.Gingell： “Single Sideband Modulation using Sequence Asymmetric Polyphase Networks” Electrical Communication Magazine， Vol 48 No 1 and 2 combined 1973， p 21-25

　　2. Pat Hawker， G3VA： “Polyphase System for SSB Generation” in “Technical Topics” Radio Communication Oct 73， p698-9

　　3. Pat Hawker， G3VA： “More on Polyphase SSB” in “Technical Topics” Radio Communication Dec 73， p852-853

　　4. M.J.Gingell： “The Synthesis and Application of Polyphase Networks with Sequence Asymmetric Properties” PhD Thesis University of London， 1975

　　5. M.J.Gingell： “Sequence Asymetric Polyphase Networks： Application to F D M” IEE Colloquium on Applications of Active， Digital and Passive Filters， London， January 141975.

　　6. Pat Hawker， G3VA： “G3PLX polyphase SSB generator” in “Technical Topics” Radio Communication May 1975， p379-381

　　7. A. Gschwindt， HA5WH： “Some Reflections on the four-way phasing method” Radio Communication Jan 76， p28-33

　　8. J.R.Hey： “Practical Polyphase SSB for shallow pockets” Radio Communication Sept 76， p656-660， 663

　　9. J Heyne： “New Active Quadrature Phase Shift Network” IEE Electronics Letters， 31 March 1977， p216-218

　　10. A G Constantinide： “Digital Phase Splitting Network Design for digital F.D.M. applications” PROC IEE， Vol 23 No 12 Dec 1976， p 1313-1315

审核编辑：黄飞