

机器学习模型偏差与方差详解
人工智能
描述
在机器学习的世界中,准确性是至关重要的。您努力通过调整和优化参数使模型更加准确,但始终无法使其达到100%的准确性。这就是关于您的预测/分类模型的残酷现实,它们永远无法是零误差的。在本文中,我将讨论为什么会发生这种情况以及其他可以减少误差的方法。
假设我们观察到一个响应变量 Y(定性或定量)和输入变量 X 具有 p 个特征或列(X1、X2.....Xp),我们假设它们之间存在关系。这种关系可以表示为
在这里,f 是一些固定但未知的 X1,…,Xp 的函数,e 是一个随机误差项,它与 X 独立,并且平均为零。在这个公式中,f 代表 X 关于 Y 提供的系统信息。对这种关系或 f(X) 的估计被称为统计学习。
一般来说,我们不能对 f(X) 进行完美估计,这导致产生一个错误项,称为可减少误差。通过更准确地估计 f(X) 从而减少可减少误差来提高模型的准确性。但是,即使我们对 f(X) 进行了100%准确的估计,我们的模型也不会是无误差的,这被称为不可减少误差(在上述方程中的 e)。
换句话说,不可减少误差可以看作是 X 无法提供关于 Y 的信息。损失量 e 可能包含未测量的对预测 Y 有用的变量:由于我们不测量它们,f 无法用于预测。损失量 e 也可能包含不可测量的变化。例如,对于给定的患者在给定的一天,不良反应的风险可能会因药物本身的制造变异或患者在当天的一般感觉良好程度而有所不同。
这样的边界情况存在于每个问题中,它们引入的误差是不可减少的,因为通常它们不存在于训练数据中。我们无法对此做任何事情。我们能做的是减少其他形式的错误,以获得 f(X) 的近乎完美的估计。但首先让我们看看机器学习中的其他重要概念,这些概念您需要了解,以便进一步学习。
模型复杂度
从数据集中学习时,输入和响应变量之间的关系 f(X) 的复杂性是需要考虑的一个重要因素。简单的关系易于解释。例如,一个线性模型看起来像这样:
从这个关系中推断信息是很容易的,而且它清楚地告诉了一个特定特征如何影响响应变量。这样的模型属于限制性模型的范畴,因为它们只能采用特定形式,比如这种情况下是线性的。但是,一个关系可能比这更复杂,例如它可能是二次的、圆形的等。这样的模型更加灵活,因为它们可以更紧密地拟合数据点,并且可以采用不同的形式。通常这种方法会导致更高的准确性。但这种灵活性是以可解释性为代价的,因为复杂的关系更难解释。
选择一个灵活的模型并不总是能够保证高准确性。这是因为我们的灵活的统计学习程序过于努力地在训练数据中寻找模式,可能会捕捉到一些仅仅由于随机机会而不是未知函数 f 的真实属性而导致的模式。这改变了我们对 f(X) 的估计,导致模型不太准,这种现象也称为过拟合。
当推断是目标时,使用简单和相对不灵活的统计学习方法有明显的优势。然而,在某些情况下,我们只对预测感兴趣,而预测模型的可解释性根本不是重点。这时我们会使用更灵活的方法。
拟合度量
为了量化对于给定观测值,预测的响应值与该观测值的真实响应值之间的接近程度,在回归设置中最常用的度量是均方误差(MSE)。
均方误差是预测值与观测值之间的误差或差异的平方的平均值。如果使用训练数据计算,则称为训练MSE,如果使用测试数据计算,则称为测试MSE。
对于给定值 x0,期望的测试MSE 总是可以分解为三个基本量的和:f(x0) 的方差、f(x0) 的平方偏差和误差项 e 的方差。其中,e 是不可减少的误差,之前我们已经讨论过。因此,让我们更多地了解偏差和方差。
偏差
偏差指的是通过用一个简单得多的模型来近似一个可能非常复杂的真实生活问题而引入的误差。因此,如果真实关系是复杂的,而你尝试使用线性回归,那么在估计 f(X) 时肯定会产生一些偏差。无论你有多少观测值,如果你在真实关系非常复杂的情况下使用简单的算法,那么就不可能产生准确的预测。
方差
方差指的是如果我们使用不同的训练数据集来估计 f(X),那么您对 f(X) 的估计会发生变化的程度。由于训练数据用于拟合统计学习方法,不同的训练数据集将导致不同的估计。但理想情况下,对于 f(X) 的估计在训练集之间不应该有太大变化。然而,如果一个方法具有高方差,则训练数据的微小变化可能导致 f(X) 发生很大变化。
偏差和方差的一般规则
数据集的任何变化都将提供一个不同的估计值,若使用统计方法过度匹配训练数据集时,这些估计值非常准确。一个一般规则是,当统计方法试图更紧密地匹配数据点,或者使用更灵活的方法时,偏差会减少,但方差会增加。
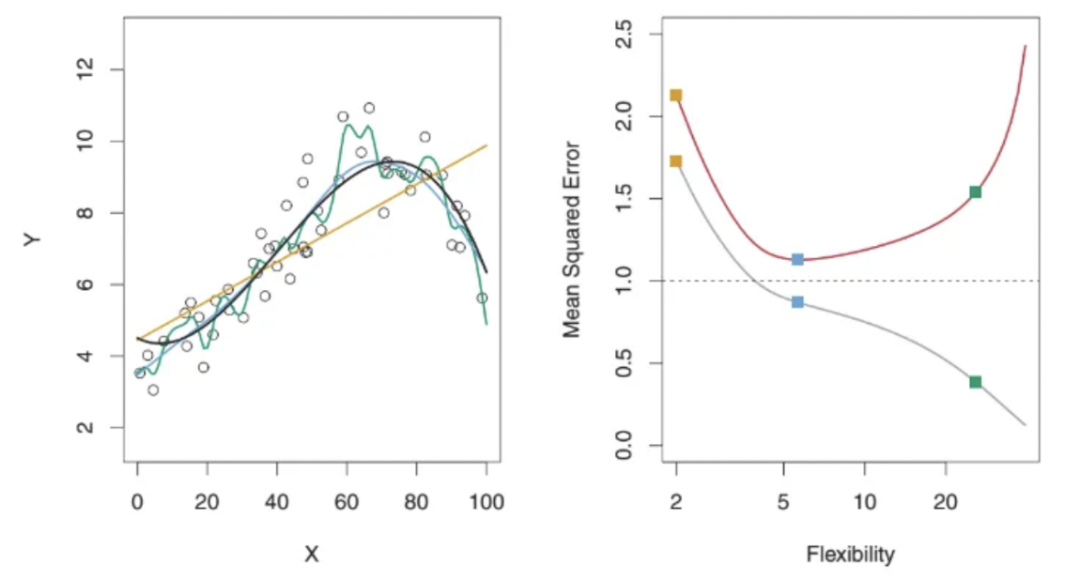
在上面的图片中,左边显示了回归设置中三种不同统计方法的图表。黄色是线性模型,蓝色是略微非线性模型,绿色是高度非线性/灵活(Flexibility)模型,因为它过分匹配数据点。在右边,您可以看到这三种方法的灵活性与 MSE 之间的图表。红色代表测试 MSE,灰色代表训练 MSE。不能确定具有最低训练 MSE 的方法也将具有最低测试 MSE。这是因为一些方法专门估计系数以最小化训练 MSE,但它们可能没有较低的测试 MSE。这个问题可以归结为过拟合的问题。如图所示,绿色曲线(最灵活的或复杂度最高的模型)具有最低的训练 MSE,但不具有最低的测试 MSE。让我们深入探讨一下这个问题。
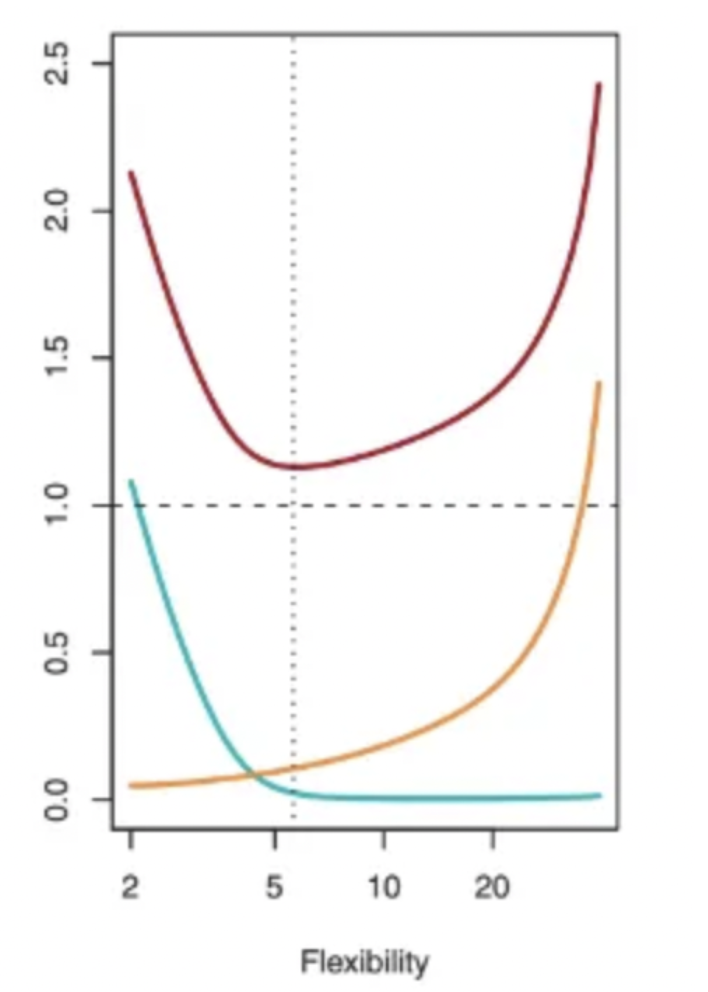
这是一个关于测试 MSE(红曲线)、偏差(绿曲线)和方差(黄曲线)随着所选择方法的灵活性而变化的图表,针对特定数据集。最低 MSE 点对于偏差和方差的错误形式提出了一个有趣的观点。它表明,随着灵活性的增加,偏差减少的速度比方差增加的速度更快。在某一点之后,偏差不再减少,但方差由于过拟合而开始迅速增加。
灵活性的含义是模型的复杂度,灵活性越高代表模型的复杂度越高
偏差-方差权衡
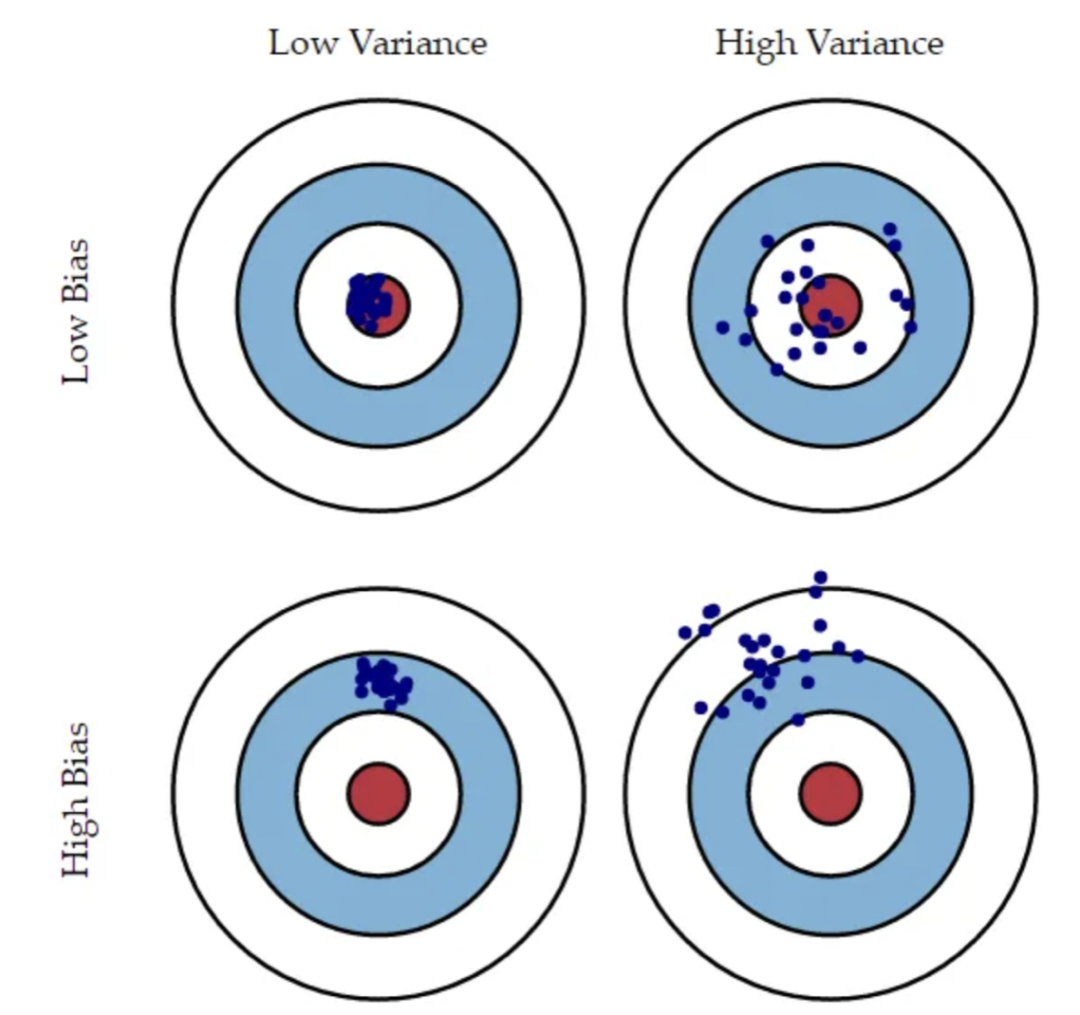
在上图中,想象一下靶心是一个完美预测正确值的模型。随着我们离靶心越远,我们的预测变得越来越糟糕。假设我们可以重复整个模型构建过程,以获得多次靶子命中情况,这样每个蓝点代表基于不同数据集对同一问题的模型的不同实现。它显示了四种不同情况,代表了高偏差和低偏差以及高方差和低方差的组合。高偏差是指所有点都远离靶心,高方差是指所有点都分散。这个图示结合了前面的解释,使得偏差和方差之间的区别非常清晰。
如上包含4个图的图表,左上图表示低偏差和低方差,右上图表示低偏差和高方差,左下图表示高偏差和低方差,右下图表示高偏差和高方差。
正如前面所述,为了最小化期望的测试误差,我们需要选择一种统计学习方法,同时实现低方差和低偏差。这两个值之间总是存在着一种权衡,因为很容易获得一个偏差极低但方差很高的方法(例如,通过绘制通过每个训练观察点的曲线)或一个方差非常低但偏差很高的方法(通过将水平线拟合到数据)。挑战在于找到一个方差和平方偏差都很低的方法。
权衡偏差和方差是成为机器学习冠军所必需的,也是模型开发过程中必须考虑的问题。在解决机器学习问题时应该牢记这一概念,因为它有助于提高模型的准确性。同时保持这种知识有助于您迅速决定不同情况下最佳的统计模型。
审核编辑:黄飞
-
机器学习模型评估指标2023-09-06 2046
-
机器算法学习比较2016-09-27 4939
-
机器学习笔试题精选2018-10-11 4330
-
机器学习模型之性能度量2020-05-12 1598
-
机器学习之偏差、方差,生成模型,判别模型,先验概率,后验概率2020-05-14 2148
-
统计函数中的标准偏差,均方根和方差的计算2021-08-11 1784
-
讲解统计函数中的标准偏差,均方根和方差的计算2021-08-17 1647
-
函数中的标准偏差/均方根和方差怎么计算?2021-11-19 2630
-
部署基于嵌入的机器学习模型2022-11-02 3492
-
机器学习中的几种数据偏差2021-01-05 3471
-
为什么要使用集成学习 机器学习建模的偏差和方差2021-08-14 3568
-
机器学习模型的可解释性算法详解2022-02-16 6096
-
如何评估机器学习模型的性能?机器学习的算法选择2023-04-04 1602
-
过拟合、泛化和偏差-方差权衡2023-06-12 963
-
机器学习算法汇总 机器学习算法分类 机器学习算法模型2023-08-17 1906
全部0条评论

快来发表一下你的评论吧 !

