一种多传感器可信度的确定方法

 

　　本文借鉴层次分析法(Analytic Hierarchy Process，AHP)中分层的思想，提出了一种确定多个传感器可信度的方法，根据信息的相对可信度，建立了多传感器可信度的判断矩阵，该矩阵的正交特征向量即为对应传感器的可信度。仿真结果证明，融合数据要优于各传感器的算术平均值(等可信度融合)。

　　1 加权平均的数据融合模型

　　设在K时刻系统有p个传感器，q个目标，对传感器i，目标j测量值为：mij(i=1，2，…，p;j=1，2，…，q)。按照加权平均的融合算法确定传感器i的可信度为ai(i=1，2，…，p)，则目标j的融合结果为：

　　

 

　　而ai(i=1，2，…，p)是需要确定的某时刻系统各传感器可信度。

　　2 层次分析法

　　T.L.Saaty于70年代提出层次分析法(AHP)，为解决多目标决策问题提供了很大的方便，在资源分配、企业管理、经济分析与计划、社会学、行为学中得到了广泛应用。其核心思想：首先，把要解决的问题分层系列化，即根据问题的性质和要达到的目标，将问题分解为不同的组成因素，按照因素之间的相互影响和隶属关系将其分层类聚组合，形成一个递阶的、有序的层次结构模型，然后，对模型中每一层次因素的相对重要性，依据人们对客观现实的判断，给予定量表示，再利用数学方法确定每一层次全部因素相对重要性次序的权值，最后，通过综合计算各层因素相对重要性的权值。

　　2.1 AHP可信度的确定

　　在多传感器探测系统中，在某时刻系统对传感器量测的信任程度，称为该时刻该传感器的可信度，针对系统中的p个传感器，q个目标。传感器对各目标的量测共有p×q个。根据q个目标分为q组，对于同一目标的量测分在一组。对于目标j，设各传感器量测的平均值：

　　

 

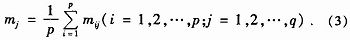
　　式中：mij表示第i个传感器对j目标的量测。

　　两个传感器s和t对目标量测可信度的比值定义如式(4)。在已知真实值时，可用真值代替平均值。

　　

 

　　该矩阵是对称阵，即

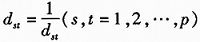
，且对角线元素为1。由式(4)，传感器量测距离平均值mj越近，该结果同其他结果的可信度比值就会越高，则判断矩阵中相应元素就会越大。对于目标j，该传感器的可信度也将会越大。判别矩阵求解可信度的步骤为：

　　(1)将判断矩阵Dj的各列作归一化处理，得到矩阵

。其中的元素一般项为：

 

　　

 

　　(2)将列归一化的判断矩阵*****按行相加，得到过渡可信度向量

。其元素的一般项为：

 

　　

 

　　(3)将过渡可信度向量

归一化，得到可信度向量Wj。其中的元素

表示第r个传感器对目标j的可信度。

 

　　

 

　　对每一组重复此过程，分别建立各目标的判断矩阵(q个)，相应得到q个可信度向量Wj(j=1，2，…，q)。传感器r(r=1，2，…，p)的综合可信度为其对各个目标量测可信度的平均值

。

 

　　3 仿真实例及误差分析

　　为验证该传感器可信度的有效性，运用java语言模拟5个传感器对地面上卡车的运动情况的探测，利用文中算法融合数据与等可信度(每个传感器赋予相同可信度)的融合结果进行比较，如图1。

　　

 

　　由图1看出，本文AHP可信度确定法的融合结果更为接近目标真实数据，优于等可信度法的融合结果。

　　分别计算AHP可信度确定法的融合结果与真实数据间的均方误差和平均距离，并与等可信度方法融合结果进行比较如表1：

　　

 

　　由表1可以看出，本文融合数据与真实数据间的均方误差和平均距离比等可信度融合结果小，验证了改可信度确定方法的有效性。

　　4 结论

　　本文借鉴层次分析法的思想，通过信息的相对可信度建立了传感器可信度矩阵，进而对所有传感器按可信度进行排序，根据传感器的可信度决定参与融合量测客观性，通过对地面卡车的融合结果进行分析，验证了该方法的有效性。