

FPGA实现双调排序方法详解
可编程逻辑
描述
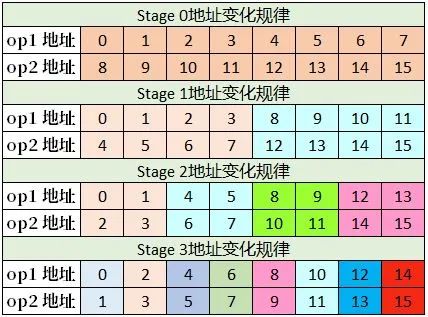
基于双调排序算法的蝶形图,我们可以得到地址的变化规律。这里以长度为16的双调序列为例,其地址变化规律入下图所示。由于长度为16,故总共需要4个Stage。图中每个Stage颜色的个数表明该Stage可分为的组数。例如Stage 0可分为1组,Stage 1可分为2组,Stage 2可分为4组,Stage 3可分为8组。
每组的起始地址和对应的Stage紧密相关,例如Stage 1第0组起始地址为0,即(16/2^1)*0,第1组起始地址为8,即(16/2^1)*1。每组的地址个数也由Stage决定。例如Stage 1每组地址长度为4,即16/2^(1+1),Stage 2每组地址长度为2,即16/2^(2+1)。同一组内,相邻地址的间距为1,例如Stage 1第0组的4个地址为[0,1,2,3],相邻地址间距为1,第1组的4个地址为[8,9,10,11],相邻地址间距为1。
一旦确定了op1的地址就很容易确定op2的地址,因为两者之差(用diff表示)也是由Stage决定的。例如:Stage 0两者之差为8,即16/2^(0+1),Stage 1两者之差为4,即16/2^(1+1)。
我们将地址规律总结为如下图所示形式。这里一个重要的数据是Stage,其与序列长度的关系可表示为Stage=log2(N);另一个重要数据为diff,其与Stage关系可表示为diff=N/2^(Stage+1)。
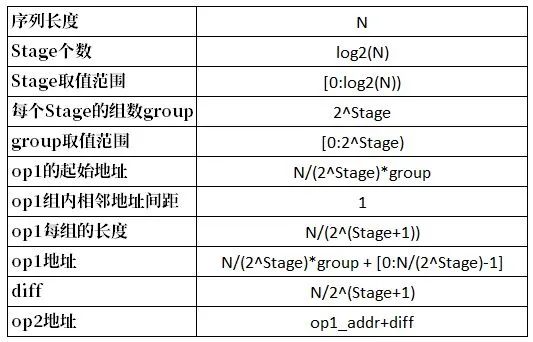
在此基础上我们就很容易借助C++或Matlab生成两个操作数的地址。这里采用Matlab,相应的Matlab函数如下图所示。代码第5行用于判断序列长度是否为2的整数次幂。
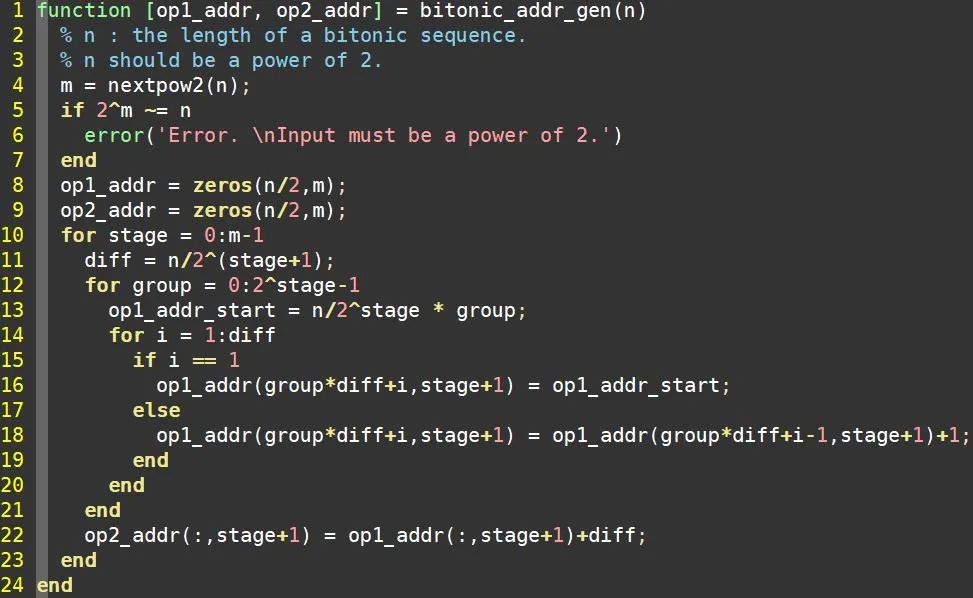
有了地址关系也就有了数据之间的关系。通常情况下,数据是按时间顺序串行进入的,所以我们也期望每次排序之后也是串行输出的。根据数据流的关系,我们可以采用单路径延迟反馈(Single-pathDelay Feedback, SDF)运算单元流水结构,SDF单元如下图所示。
图中butterfly为蝶形运算单元,(2^P)D为延迟单元,延迟级数与所在Stage相关。仍以长度为16的双调序列为例,Stage 为0时,延迟级数为8,Stage 为1时,延迟级数为4,Stage为2时,延迟级数为2,Stage为3时延迟级数为1。图中sel为分频信号,仍与Stage相关,Stage为0时,sel为时钟的8分频信号,不难看出,分频系数与延迟级数是一致的。
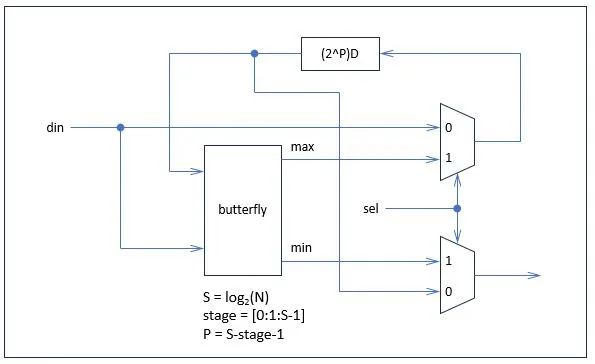
在此基础上,将4个SDF相连即可实现串行输入/串行输出的双调排序。下图给出了Stage 0对应的SDF结构。
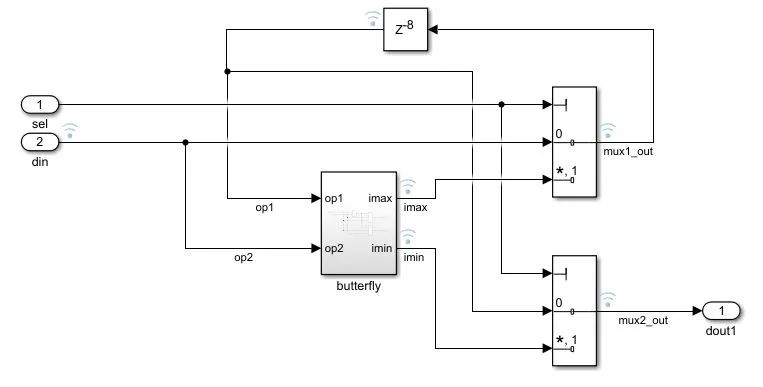
下图显示了相应的仿真结果。
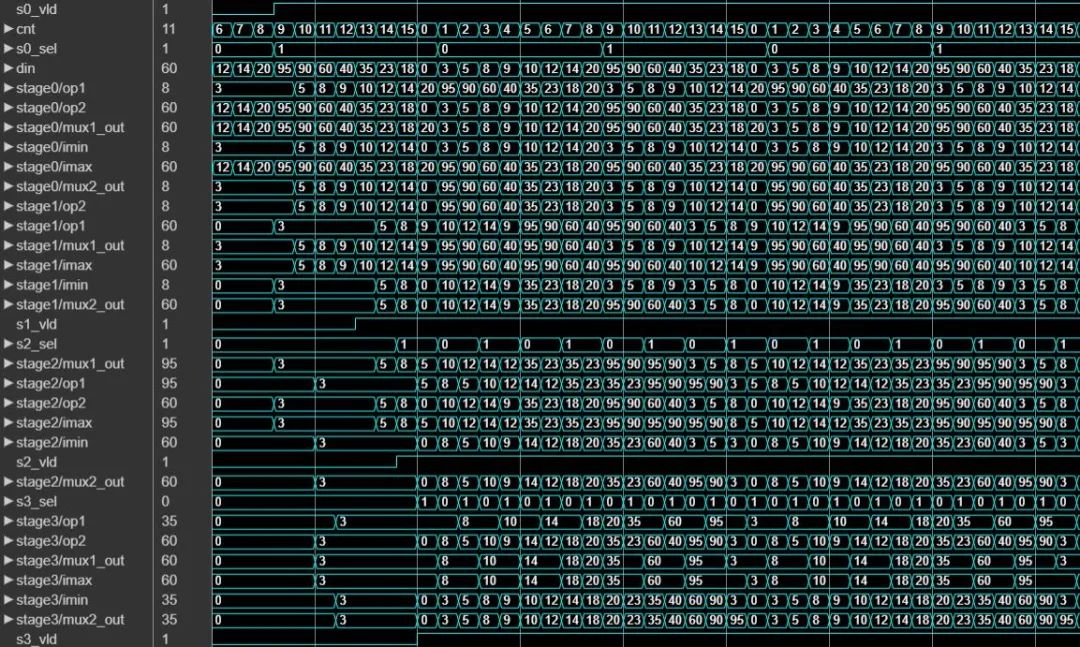
审核编辑:黄飞
- 相关推荐
- 热点推荐
- FPGA
-
干货 | 详解 FPGA 电源排序的四种方案2019-06-12 7267
-
详解FPGA电源排序的四种方案2023-05-24 1266
-
FPGA排序-冒泡排序介绍2023-07-17 1585
-
详解 FPGA 电源排序的四种方案2019-06-10 2945
-
四种FPGA 电源排序方案2019-09-17 3145
-
如何选择FPGA电源排序?这几个方法交给你2020-04-27 2329
-
算法的原理是什么?基数排序是如何实现的?2021-07-05 1867
-
冒泡排序法的具体实现方法是什么?2021-07-15 1225
-
qsort排序方法2010-08-25 649
-
FPGA时分多址的改进型实现方法2011-01-15 439
-
基于FPGA的安检机图像数据排序算法实现2018-04-26 964
-
分析FPGA 电源排序的四种方案介绍2019-09-15 1185
-
用于实现电源排序的各种方法2023-09-14 343
-
FPGA实现双调排序算法的探索与实践2024-03-14 1460
-
用FPGA实现双调排序的方法(2)2024-03-21 1393
全部0条评论

快来发表一下你的评论吧 !

