

浅谈传感器和镜头的匹配设计
MEMS/传感技术
描述
传感器和镜头的匹配设计
奈奎斯特频率成像
在奈奎斯特频率下成像是吸引人的,该频率在高级镜头选择的等式1中定义。然而,这通常不是一个好主意,因为这意味着正在观察的特征正好落在一个像素上。如果成像系统移动半个像素,则感兴趣的对象将落在两个像素之间,并且将完全模糊。因此,不建议在奈奎斯特频率下成像。假设没有使用子像素插值,通常建议在奈奎斯特频率的一半处成像,因为这将允许感兴趣的特征总是占据至少两个像素。
通常不恰当地做出的另一个假设是,除非镜头在与其一起使用的传感器的奈奎斯特频率下具有相当大(>20%)的对比度,否则该镜头不适合与特定相机一起使用。事实并非如此。如前所述,在奈奎斯特极限下成像是不明智的,可能会产生几个问题。需要查看整个系统,以确定镜头是否适合给定的相机传感器,这通常取决于应用。下一节将介绍在奈奎斯特频率或接近奈奎斯特频率时成像系统中发生的情况,以及对整体系统分辨率的影响。
理解相机传感器和成像镜头之间的相互作用是设计和实现机器视觉系统的重要部分。这种关系的优化常常被忽视,它对系统整体分辨率的影响很大。不正确配对的相机/镜头组合可能导致在成像系统上浪费金钱。不幸的是,决定在任何应用中使用哪个镜头和相机并不总是一件容易的事:更多的相机传感器(直接结果是更多的镜头)继续被设计和制造,以利用新的制造能力并提高性能。这些新的传感器为镜头带来了许多需要克服的挑战,并使正确的相机与镜头配对变得不那么明显。
第一个挑战是像素继续变小。虽然较小的像素通常意味着较高的系统级分辨率,但一旦考虑到所使用的光学器件,情况并非总是如此。在一个完美的世界里,系统中没有衍射或光学误差,分辨率将简单地基于像素的大小和被观察物体的大小(见分辨率)。简而言之,当像素尺寸减小时,分辨率增加。当较小的对象可以适合较小的像素并且仍然能够分辨对象之间的间距时,即使该间距减小,也会发生这种增加。这是一个关于相机传感器如何检测物体的过于简化的模型,没有考虑噪声或其他参数。
镜头也有分辨率规格,但基本原理并不像传感器那样容易理解,因为没有像像素那样具体的东西。然而,当通过镜头成像时,有两个因素最终决定特定物体特征在像素上的对比度再现(调制传递函数或MTF):衍射和像差内容。任何时候光通过光圈都会发生衍射,导致对比度降低(艾里斑和衍射极限中的更多细节)。像差是发生在每个成像镜头中的误差,其根据像差的类型而模糊或错位图像信息,如真实世界性能中所述。对于快镜头(≤f/4),光学像差通常是系统偏离衍射极限所规定的“完美”的原因;在大多数情况下,如公式1所示,镜头在其理论截止频率(ξcutoffξcutoff)下根本不起作用。
将这个等式与相机传感器联系起来,随着像素频率的增加(像素大小下降),对比度下降-每个镜头都会遵循这一趋势。然而,这并不能说明镜头的真实硬件性能。镜头的公差和制造的紧密程度也将对镜头的像差内容产生影响,并且真实世界的性能将不同于标称的设计性能。根据标称数据来估计真实世界镜头的表现可能会有差异,但实验室中的测试可以帮助确定特定镜头和相机传感器是否兼容。
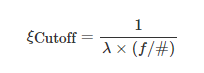
(1)
了解镜头在特定传感器上的表现的一种方法是用美国空军1951年的棒靶测试其分辨率。条形目标比星形目标更适合确定镜头/传感器的兼容性,因为它们的特征与正方形(和矩形)像素排列得更好。以下示例显示了使用相同的高分辨率50mm焦距镜头和相同的照明条件在三个不同的相机传感器上拍摄的测试图像。然后将每个图像与镜头的标称轴上MTF曲线(蓝色曲线)进行比较。在这种情况下仅使用轴上曲线,因为测量对比度的感兴趣区域仅覆盖传感器中心的一小部分。图1A显示了50mm镜头与具有2.2µm像素的1/2.51/2.5ON Semiconductor MT9P031配对时的性能,放大倍率为0.177倍。
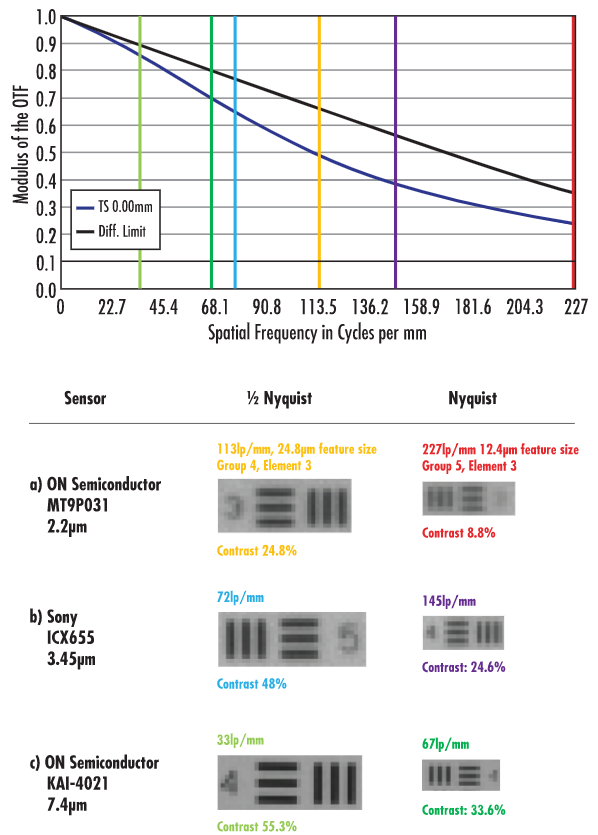
图1:(a)2.2μm像素的ONSemiconductor MT9P031、(B)3.45μm像素的SonyIXC655和(C)7.4μm像素的ONSemiconductorKai-4021上的高分辨率50mm镜头的标称镜头性能与实际性能的比较。红线、紫线和深绿线分别表示传感器的奈奎斯特极限。黄线、浅蓝线和浅绿线分别表示传感器奈奎斯特限值的一半。
使用分辨率公式1,传感器的奈奎斯特分辨率(ξsensor)为227.7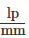 ,这意味着系统在放大倍率为0.177x时理论上可以成像的最小物体为12.4µm(使用分辨率公式1的替代形式)。
,这意味着系统在放大倍率为0.177x时理论上可以成像的最小物体为12.4µm(使用分辨率公式1的替代形式)。
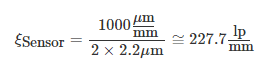
(2)
请记住,这些计算没有与之关联的对比度值。图1A的左侧显示了美国空军1951目标上的两个元素的图像;左图显示每个特征两个像素,右图显示每个特征一个像素。在传感器(227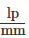 )的奈奎斯特频率下,系统以8.8%的对比度对目标成像,该对比度低于可靠成像系统所推荐的20%的最小对比度。注意,通过将特征尺寸增加两倍至24.8μm,对比度增加了近三倍。在实际意义上,成像系统在奈奎斯特频率的一半处将可靠得多。
)的奈奎斯特频率下,系统以8.8%的对比度对目标成像,该对比度低于可靠成像系统所推荐的20%的最小对比度。注意,通过将特征尺寸增加两倍至24.8μm,对比度增加了近三倍。在实际意义上,成像系统在奈奎斯特频率的一半处将可靠得多。
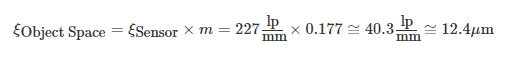
(3)
成像系统不能可靠地对尺寸为12.4µm的物体特征进行成像,这一结论与分辨率方程所示的结论截然相反,因为从数学上讲,物体在系统的能力范围内。这一矛盾突出表明,一阶计算和近似不足以确定成像系统是否能够达到特定的分辨率。此外,奈奎斯特频率计算并不是为系统的分辨率能力奠定基础的可靠指标,只能用作系统将具有的限制的指南。8.8%的对比度太低而不能被认为是准确的,因为条件的微小波动很容易将对比度降低到无法分辨的水平。
图1B和1C显示的图像与MT9P031上的图像类似,但使用的传感器是索尼ICX655(3.45µm像素)和安森美半导体Kai-4021(7.4µm像素)。每个图中的左侧图像显示每个特征两个像素,右侧图像显示每个特征一个像素。这3个图之间的主要区别在于,图1B和1C的所有图像对比度都在20%以上,这意味着(乍一看)它们在分辨该尺寸的特征时是可靠的。当然,与图1A中的2.2µm像素相比,它们可以分辨的最小尺寸对象更大。然而,在奈奎斯特频率下成像仍然是不明智的,因为物体的轻微移动可能会使两个像素之间的所需特征发生偏移,从而使物体无法分辨。请注意,当像素尺寸从2.2µm增加到3.45µm,再增加到7.4µm时,对比度从每个特征一个像素增加到每个特征两个像素的影响较小。在ICX655(3.45µm像素)上,对比度变化略低于2倍;Kai-4021(7.4µm像素)进一步减弱了这种影响。

图2:在三种不同像素大小的相机传感器上,使用相同的镜头和光照条件拍摄的图像。顶部图像以每个特征四个像素拍摄,底部图像以每个特征两个像素拍摄。
图1中的一个重要差异是标称镜头MTF与实际图像中的真实对比度之间的差异。图1A顶部的镜头的MTF曲线显示,当产生的对比度值为8.8%时,镜头在频率227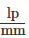 处应达到约24%的对比度。造成这种差异的主要因素有两个:传感器MTF和镜头公差。大多数传感器公司不公布其传感器的MTF曲线,但它们具有与镜头相同的一般形状。由于系统级MTF是系统的所有部件的MTF的乘积,因此镜头和传感器的MTF必须相乘在一起,以提供系统的整体分辨率能力的更精确的结论。
处应达到约24%的对比度。造成这种差异的主要因素有两个:传感器MTF和镜头公差。大多数传感器公司不公布其传感器的MTF曲线,但它们具有与镜头相同的一般形状。由于系统级MTF是系统的所有部件的MTF的乘积,因此镜头和传感器的MTF必须相乘在一起,以提供系统的整体分辨率能力的更精确的结论。
如上所述,镜头的公差MTF也是偏离标称值。所有这些因素共同改变了系统的预期分辨率,就其本身而言,镜头MTF曲线并不是系统级分辨率的准确表示。
如图2中的图像所示,最佳系统级对比度出现在使用较大像素拍摄的图像中。当像素尺寸减小时,对比度显著下降。一个好的最佳实践是使用20%作为机器视觉系统中的最小对比度,因为低于该对比度的任何对比度值都太容易受到来自温度变化或照明串扰的噪声波动的影响。使用50mm镜头和图1A中的2.2µm像素拍摄的图像的对比度为8.8%,由于镜头即将成为系统中的限制因素,因此对于与2.2µm像素尺寸相对应的物体特征尺寸,图像数据太低,无法依赖图像数据。像素远小于2.2µm的传感器当然存在,并且非常受欢迎,但远小于该尺寸的传感器几乎不可能让光学器件分辨到单个像素级别。这意味着在分辨率中描述的方程对于帮助确定系统级分辨率在功能上变得毫无意义,并且类似于在上述图中拍摄的图像将不可能被捕获。然而,这些微小的像素仍然有用处——仅仅因为光学不能分辨整个像素并不会使它们变得无用。对于某些算法,如斑点分析或光学字符识别(OCR),它不是关于镜头是否可以实际分辨到单个像素级别,而是关于可以在特定特征上放置多少像素。对于较小的像素,可以避免子像素插值,这将增加用它进行的任何测量的精度。此外,当切换到具有拜耳模式滤波器的彩色相机时,在分辨率损失方面的损失较小。
要记住的另一个要点是,从每个特征一个像素跳到每个特征两个像素会产生大量的对比度,特别是在较小的像素上。尽管通过将频率减半,最小可分辨物体的大小实际上增加了一倍。如果绝对有必要观察到单像素水平,通常最好将光学放大倍数加倍,并将视场(FOV)减半。
这将导致特征尺寸覆盖两倍的像素,并且对比度将高得多。这种解决方案的缺点是整个场的可见度较低。从图像传感器的角度来看,最好的做法是保持像素大小,并将图像传感器的格式大小加倍。例如,使用具有2.2µm像素的½“传感器的1倍放大成像系统将具有与使用具有2.2µm像素的1”传感器的2倍放大系统相同的FOV和空间分辨率,但使用2倍系统,对比度理论上加倍。
不幸的是,将传感器尺寸加倍会给镜头带来额外的问题。成像镜头的主要成本驱动因素之一是其设计的格式尺寸。为较大规格的传感器设计物镜需要更多单独的光学元件;这些部件需要更大,并且系统的公差需要更严格。继续上面的例子,为1“传感器设计的镜头的成本可能是为½”传感器设计的镜头的五倍,即使它不能达到相同的像素限制分辨率规格。
审核编辑:黄飞
-
多镜头多传感器图像视频处理器应用2024-01-26 1356
-
如何选择图像传感器的镜头2024-01-16 1972
-
浅谈工业相机镜头的参数与选型2023-11-03 521
-
加速度传感器怎么匹配2023-07-07 1814
-
土壤水分传感器选择依据浅谈分享2023-02-09 843
-
各种特定尺寸传感器兼容的工业相机镜头接口设计2023-01-12 1557
-
浅谈压力传感器的使用方法及注意事项2021-03-10 1703
-
指纹验证:主芯片上匹配和传感器内匹配有何不同?2018-11-08 1632
-
视觉传感器型号了解2017-09-20 652
-
浅谈热释电红外线传感器RE200B的应用(免费下载)2012-08-20 9680
-
浅谈热释电红外线传感器RE200B的应用2012-08-14 2697
-
浅谈变送器与传感器区别及联系2010-01-28 959
全部0条评论

快来发表一下你的评论吧 !

