中国铁路网的Dijkstra算法实现案例

1. 项目概述

项目说明

该项目分别在DE1-SOC开发板的FPGA和HPS上实现了Dijkstra算法，能在中国铁路网中找到两站之间的最短距离和路线。

这个项目包含304个中国主要火车站。运行程序时，首先在VGA上显示包含所有火车站及站点之间连线的完整地图：

然后用户可以通过输入两个站点的名称，或在VGA屏幕相应的站点上点击鼠标以选择任意两个站点作为起点和目的地，程序会根据Dijkstra算法很快返回它们之间的最小距离、沿路站点以及计算所耗费时长，并在VGA显示器上显示出详细的路线。

最后他们将两套方案进行了对比，结果显示Dijkstra算法在FPGA上实现比仅在HPS上实现的计算速度快10倍。所以利用FPGA并行数据处理的优势来加速Dijkstra算法是个非常不错的选择。

2. Dijkstra算法

Dijkstra算法用于计算点网络中两点之间的最小距离和路径。由计算机科学家Edsger W. Dijkstra于1956年提出。下图是这个算法的一个概念解释:

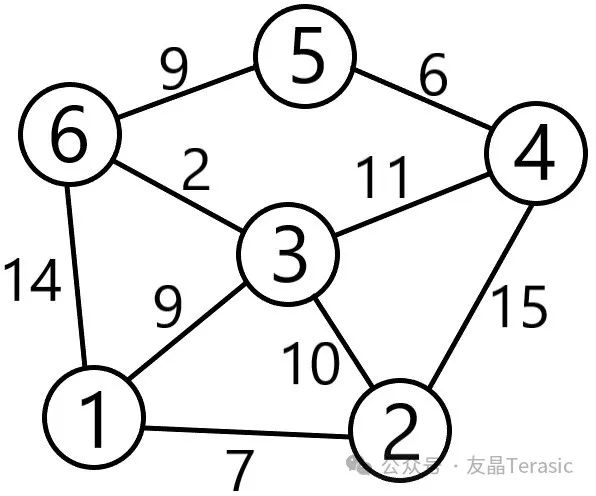
圆圈内的数字代表火车站，连接两个圆的线代表铁路，线旁边的数字是铁路的距离。例如，从1号站到4号站有多种选择，Dijkstra算法将帮助我们找到1号站到4号站的最短距离。

表1红框中的第1行表示节点1与其他每个节点之间的最小距离。

表1

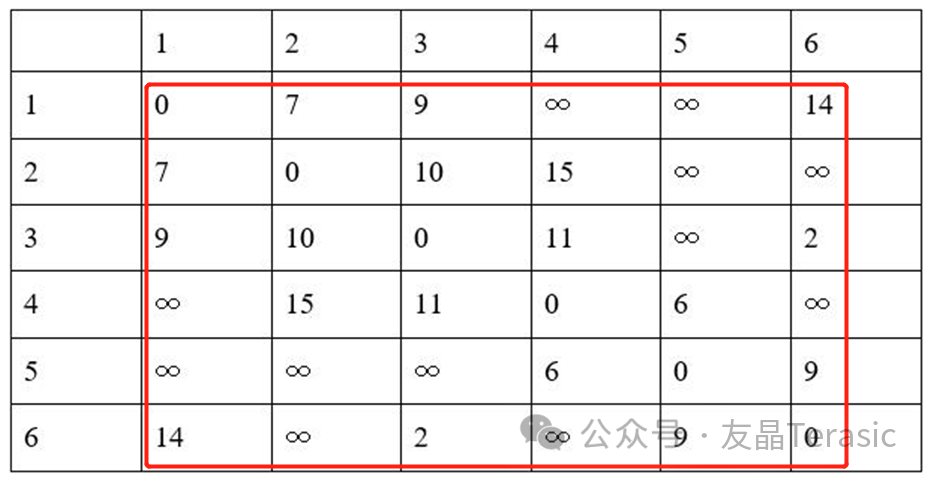
把1当作起点。为了获得 1 与其余每个站点之间的最小距离，需多次更新表1红框中的第 1 行。

首先，从点 1 到点 1 本身，距离为 0，这肯定是最短，因此不会再更新这个值，这里把0设定为固定值。

然后找到表1红框第 1 行中与1连接的最小距离对应的点，即距离为7的点 2 。此时不会再更新 7这个值，因为可以确保它是从点 1 到点 2 的最短距离。这里把7设定为固定值。

接下来，点2 将被视为下一个起点。如果第 1 行 x 列的距离大于第 1 行第 2 列和第 2 行 x 列的距离之和，则将第 1 行 x 列更新为距离之和。x 可以来自 {3,4,5,6} 中的任意数字。这样第一行就更新如下：

表2

现在，除了固定值 0 和 7 之外，第 1 行中的最小值是 9，对应于点 3。它是从点 1 到点 3 的最短距离，所以此处9也被设定为固定值。

接下来，第 1 行将从第 3列更新。如果第1行x列的距离大于第1行第3列和第3行x列的距离之和，则将第1行x列更新为距离之和。x 可以来自 {4,5,6} 中的任意数字。第 1 行更新为：

表3

用同样的方法，分别更新第1行的4、5和6列。结果如下所示：

表4

这样就得到了点1与其他每个节点之间的最小距离。

审核编辑：刘清