3D视觉相机模型与标定详解

1. 相机模型

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程能够用一个几何模型进行描述。这类模型有很多种，其中最简单的称为针孔模型。针孔模型是很常用，而且有效的模型，它描述了一束光线通过针孔之后，在针孔背面投影成像的关系。同时，由于相机镜头上的透镜的存在，会使得光线投影到成像平面的过程中会产生畸变。因此，我们使用针孔和畸变两个模型来描述整个投影过程。

1.1 针孔相机模型

在物理课堂上，我们可能都见过一个蜡烛投影实验：在一个暗箱的前方放着一支点燃的蜡烛，蜡烛的光透过暗箱上的一个小孔投影在暗箱的后方平面上，并在这个平面上形成了一个倒立的蜡烛图像。在这个过程中，针孔模型能够把三维世界中的蜡烛投影到个二维成像平面。

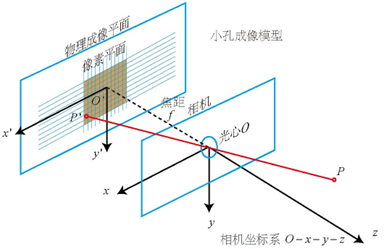
图1：针孔相机模型

如图1所示，来对这个简单的针孔相机模型进行几何建模。设O-x-y-z为相机坐标系，习惯我们让z轴指向相机前方，x向右，y向下，O为摄像机的光心，也是针孔模型中的针孔。

P为相机坐标系下的一点，经过小孔O投影之后，落在物理成像平面O′-x′-y′上，成像点为P′，并且设物理成像平面到小孔的距离为f(焦距)。

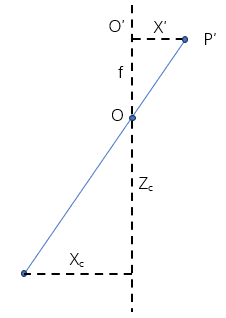
图2：针孔相机模型的三角形关系

那么，如图2所示，根据三角形相似关系，有

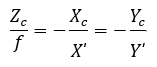
上式中，负号表示成的像是倒立的。

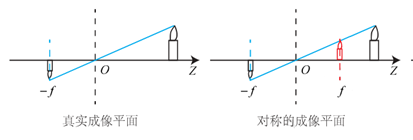
图3：针孔模型的简化

为了简化模型，如图3所示，我们把可以成像平面对称到相机前方，和三维空间点一起放在摄像机坐标系的同一侧，这样做可以把公式中的负号去掉，使公式更加简洁：

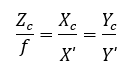
把成像平面放在摄像机坐标系的同一侧，这是一种我们处理真实世界与相机投影的数学手段，并且，大多数相机输出的图像并不是倒像，相机自身的软件会帮你翻转这张图像，所以你看到的一般是正着的像，也就是对称的成像平面上的像。所以，尽管从物理原理来说，小孔成像应该是倒像，但由于我们对图像作了预处理，所以理解成在对称平面上的像，并不会有影响。

整理后得到：

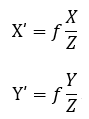
上面两式描述了点P和它的像P′之间的空间关系。

1.2 各个坐标系的定义

1）世界坐标系（world coordinate）

以被测物体上的点作为参考，定义的绝对坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置，单位是米。

2）相机坐标系（camera coordinate）

以相机光心为坐标原点，主光轴上物体方朝焦点方向为z轴，平行于sensor平面的两条垂直边分别为x和y轴，单位是米。

3）图像坐标系（film coordinate）

以主光轴与sensor的交点为坐标原点，平行于sensor平面的两条垂直边分别为x和y轴，这个平面是建立在实际成像面上的，是个二维坐标系，单位是毫米。

4）像素坐标系（pixel coordinate）:

平行于sensor的虚拟成像平面，左上角顶点为原点，x轴和y轴都平行于图像平面，以像素为单位。

1.3 坐标系转换

1.3.1 从世界坐标系到相机坐标系

由于相机在运动，所以点P的相机坐标Pc应该是它的世界坐标Pw，根据相机的当前位姿，变换到相机坐标系下的结果。相机的位姿由它的旋转矩阵R和平移向量t来描述。那么有

刚体变换公式为

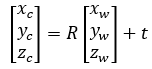
齐次坐标形式为

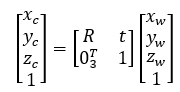
1.3.2 从相机坐标系到图像坐标系

从相机坐标系到图像坐标系就是直接运用针孔成像原理。

齐次坐标形式为

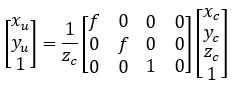
1.3.3 从图像坐标系到像素坐标系

像素坐标系通常的定义方式是：原点o′位于图像的左上角，u轴向右与x轴平行，v轴向下与y轴平行。像素坐标系与成像平面之间，相差了一个缩放和一个原点的平移。

用数学式表达如下

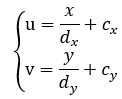
齐次坐标形式为

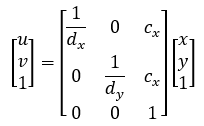
dx，dy：表示图像单个像素的宽和高，单位为mm/pixel；

(cx,cy)：表示图像中心点的像素坐标，即主光轴与sensor平面的交点。

1.3.4 从相机坐标系到像素坐标系

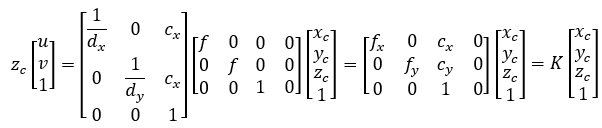
上式中，

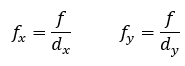
其中，fx、fy的单位为像素。

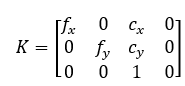
我们把中间的量组成的矩阵称为相机的内参数矩阵K。

通常认为，相机的内参在出厂之后是固定的，不会在使用过程中发生变化。有的相机生产厂商会告诉你相机的内参，而有时需要你自己确定相机的内参，也就是标定。

1.3.5从世界坐标系到像素坐标系

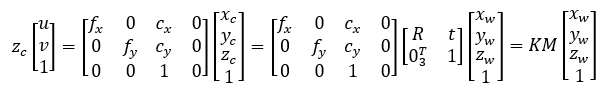
其中

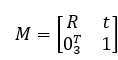
我们把旋转矩阵R和平移向量t组成的矩阵称为相机的外参数矩阵M。

相比于不变的内参，外参会随着相机运动发生改变。

内参K与外参M的乘积，是一个3×4的矩阵，称为投影矩阵，该矩阵可体现任意空间点的图像像素坐标与世界坐标之间的关系。

通过从世界坐标系到像素坐标系的公式可知，若已知投影矩阵和空间点世界坐标，则可求得空间点的像素坐标，因此，在线性模型中，一个物点在成像平面上对应唯一的像点。但反过来，若已知像素坐标和投影矩阵，代入以上公式，只能得到关于空间点世界坐标的两个线性方程，这两个线性方程表示的是像点和光心的连线，即连线上所有点都对应着该像点，由此可知，在线性模型中，一个像点对应的物点并不具有唯一性，因此，只通过一幅图像对图像场景进行三维重建是不现实的。

1.3.6 齐次坐标

为了描述人眼对物体有“近大远小”的处理（视角），也就是投影透视，便引入齐次坐标来描述。简单地说，齐次坐标是用N+1维去描述一个N维的坐标。

齐次坐标与笛卡尔坐标的转化关系：

笛卡尔坐标：(x/w, y/w)——齐次坐标：(x, y, w)

假如齐次坐标系下的坐标为(1,3, 5)，那么，转换到笛卡尔坐标系下的坐标即为(1/5, 3/5)；同理，假如齐次坐标系下的坐标为(2, 6, 10)，那么转换到笛卡尔坐标系下的坐标即为(2/10, 6/10)，化简后其值仍为(1/5, 3/5)……于是我们就可以知道：对于这个例子来说，齐次坐标系下任何形式为(1a,3a, 5a)的坐标(a不为0)在笛卡尔坐标系下都代表着同一个坐标(1/5, 3/5)，类似地，便有了“齐次”的说法，由此也引出了齐次坐标的“伸缩不变性”。

用齐次坐标进行仿射几何变换

现在，我们用笛卡尔坐标定义两条直线：

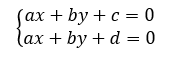
在这种情况下，这两条直线不可能相交。

转换到齐次坐标表示为

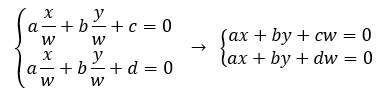
此时，w=0时有解，其交点为(x, y, 0)，同时，w=0表示这个点在无穷远处，于是两条平行线在无穷远处可相交。

齐次坐标在图形学和计算机视觉中是一个很重要的概念，一方面是因为它更易于进行仿射几何变换，另一方面也能够用来明确区分向量和点。

用齐次坐标区分向量和点

假设我们在齐次坐标系下找到了这样一组基：

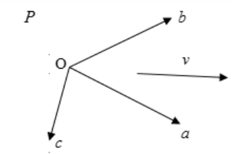
图4

于是，我们可以找到一组系数(v1,v2, v3)，将向量v表示成：

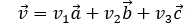
对于齐次坐标系下的一个点p，可以表示成位置向量

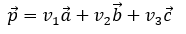
将上面两个式子均写成齐次坐标系下的矩阵形式：

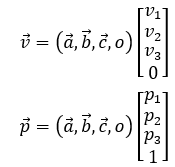
我们可以看到，(a,b,c,o)为坐标基矩阵，右侧列向量分别为向量v和点p在齐次坐标系下的坐标。于是，若想在齐次坐标系下的三维坐标中表示向量，则第四项系数为0，若想表示点，则第四项系数为1，这样就可以很方便地区分出点或者向量了。

1.4 畸变模型

为了获得好的成像效果，我们在相机的前方加了透镜。透镜的加入对成像过程中光线的传播会产生新的影响：一是透镜自身的形状对光线传播的影响，二是在机械组装过程中，透镜和成像平面不可能完全平行，这也会使得光线穿过透镜投影到成像面时的位置发生变化。

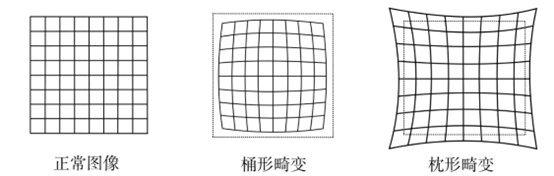
图5：畸变

在针孔模型中，一条直线投影到像素平面上还是一条直线。可是，在实际拍摄的照片中，摄像机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘，这种现象越明显。由于实际加工制作的透镜往往是中心对称的，这使得不规则的畸变通常径向对称。它们主要分为两大类，桶形畸变和枕形畸变。

桶形畸变是由于图像放大率随着离光轴的距离增加而减小，而枕形畸变却恰好相反。

在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。

除了透镜的形状会引入径向畸变外，在相机的组装过程中由于不能使得透镜和成像面严格平行也会引入切向畸变。

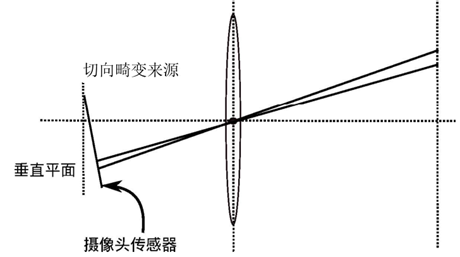
图6：切向畸变来源示意图

为更好地理解径向畸变和切向畸变，可以用更严格的数学形式对两者进行描述。我们知道平面上的任意一点p可以用笛卡尔坐标表示为[x,y]T，也可以把它写成极坐标的形式[r,θ]T，其中r表示点p离坐标系原点的距离，θ表示和水平轴的夹角。径向畸变可看成，坐标点沿着长度方向发生了变化δr，也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化δθ。

对于径向畸变，无论是桶形畸变还是枕形畸变，由于它们都是随着离中心的距离增加而增加。我们可以用一个多项式函数来描述畸变前后的坐标变化：这类畸变可以用和距中心距离有关的二次及高次多项式函数进行校正：

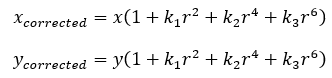
其中[x,y]T是未校正的点的坐标，[xcorrected,ycorrected]T是校正后的点的坐标，注意它们都是归一化平面上的点，而不是像素平面上的点。

在校正模型中，对于畸变较小的图像中心区域，畸变校正主要是k1起作用。而对于畸变较大的边缘区域主要是k2起作用。普通摄像头用这两个系数就能很好的校正径向畸变。对畸变很大的摄像头，比如鱼眼镜头，可以加入k3畸变项对畸变进行校正。

另一方面，对于切向畸变，可以使用另外的两个参数p1,p2来进行校正：

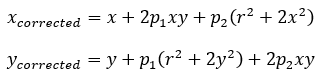
因此，联合上面两式，对于相机坐标系中的一点P(X,Y,Z)，我们能够通过五个畸变系数找到这个点在像素平面上的正确位置：

（1）将三维空间点投影到归一化图像平面。设它的归一化坐标为[x,y]T

（2）对归一化平面上的点进行径向畸变和切向畸变校正。

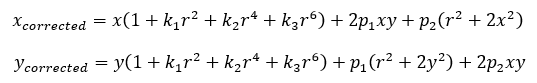
（3）将校正后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置。

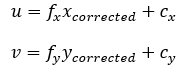
在上面的校正畸变的过程中，我们使用了五个畸变项。实际应用中，可以灵活选择校正模型，比如只选择k1,p1,p2这三项等。

1.5标定建模

综合以上描述的内容，我们可以把相机的成像模型，或者说相机标定的数学模型看成一个理想的模型加一个误差模型，理想模型就是针孔相机模型，误差模型就是畸变引起的一个误差。

结合针孔相机模型+镜头畸变，那么相机标定模型的建立过程如图7所示：

图7：标定建模的过程（坐标系转换）

标定数学模型为：

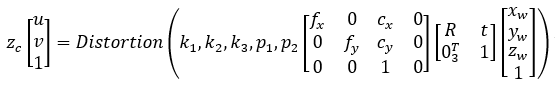
整个流程的总结：世界坐标系中的一点，通过刚体变换到相机坐标系下，再通过针孔成像的原理变换到图像坐标系，然后归一化到单位焦平面上去做去畸变处理，最后就是把图像进行数字化处理，转化到像素坐标系上。

1.6标定算法

标定算法的基本思路是在较高精度的2D-3D对应点基础上，先采用DLT或张正友方法求初值，然后非线性优化迭代求解精确解。

1.6.1直接线性标定法DLT

Abdel-Aziz和Karara于20世纪70年代初提出了直接线性变换DLT（direct linear transformation）的摄像机标定方法，这种方法忽略摄像机畸变引起的误差，直接利用线性成像模型，通过求解线性方程组得到摄像机的参数。

DLT方法的优点是计算速度很快，操作简单且易实现；缺点是由于没有考虑摄像机镜头的畸变，因此不适合畸变系数很大的镜头，否则会带来很大误差。

DLT标定法需要将一个特制的立方体标定模板放置在所需标定摄像机前，其中标定模板上的标定点相对于世界坐标系的位置已知。

首先，由立体标定参照物图像求取投影矩阵的算法，公式如下：

上式中，（Xwi，Ywi，Zwi）为空间第i个点的坐标；（ui，vi）为第i个点的图像坐标；mij为空间任意一点投影矩阵的第i行j列元素。

从上式可以得到三组线性方程，

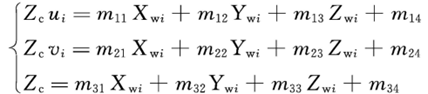
将上式方程消去Zc得到两个关于mij的线性方程。

这个式子表明，如果在三维空间中，已知n个标定点，其中各标定点的空间坐标为（Xwi，Ywi，Zwi），图像坐标为（ui，vi）（i=1，…，n），则可得到2n个关于M矩阵元素的线性方程，且该2n个线性方程可以用下面所示的矩阵形式来表示。

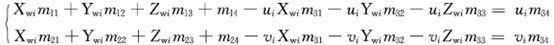
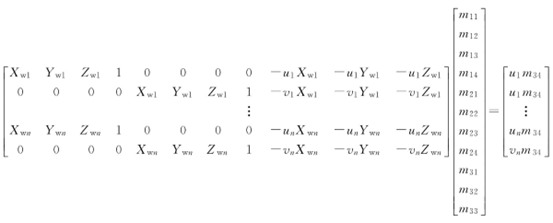
由此可见，投影矩阵乘以任意不为零的常数并不影响（Xwi，Ywi，Zwi）与（ui，vi）的关系，因此，假设m34=1，从而得到关于M矩阵其他元素的2n个线性方程，其中线性方程中包含11个未知量，并将未知量用向量表示，即11维向量m，化简得到：

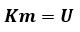
K、U为已知向量。当2n>11时，利用最小二乘法对上述线性方程进行求解：

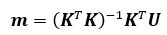
若已知空间中至少6个已知点和与之对应的图像点坐标，便可求得投影矩阵。一般采用在标定的参照物上选取个数多于6个已知点，使方程的个数远远超过未知量的个数，从而降低用最小二乘法求解造成的误差。

1.6.2张正友标定法

张正友标定法，也称Zhang标定法，是由微软研究院的张正友博士于1998年提出的一种介于传统标定方法和自标定方法之间的平面标定法。它既避免了传统标定方法设备要求高、操作繁琐等缺点，又比自标定的精度高、鲁棒性好。

图8：黑白格标定板

张正友标定法的主要步骤如下：

1）一张贴在一块刚性平面上的黑白棋盘方格图案的标定板；

2）移动标定板或者相机，从不同角度拍摄若干照片（理论上照片越多，误差越小）；

3）对每张照片中的角点进行检测，确定角点的图像坐标与实际坐标；

4）在不考虑径向畸变的前提下，即采用相机的线性模型。根据旋转矩阵的正交性，通过求解线性方程，获得摄像机的内部参数和第一幅图的外部参数；

5）利用最小二乘法估算相机的径向畸变系数；

6）根据再投影误差最小准则，对内外参数进行优化。

张正友标定法原理简介

假设我们提供K个棋盘图像，每个棋盘有N个角点，于是我们拥有2KN个约束方程。与此同时，忽略畸变的情况下，我们就需要求解4个内参和6K个外参（内参只于相机内部参数有关，外参却随目标点位置变化而变化），也就是说，只有当2KN≥4+6K的时候，也即K(N-3) ≥2时，才能求出内外参矩阵。同时，无论在一张棋盘上检测到多少角点，由于棋盘上角点的规则布置使得真正能利用上的角点只有4个（在四个方向上可延展成不同的矩形），于是有当N=4时，K(4-3) ≥2，即K≥2，也就是说，我们至少需要两张棋盘格在不同方位的图像才能求解出无畸变条件下的内参和外参。

实际上，我们往往会在一张棋盘格上布置更多的角点，因为这样就可以通过最小二乘法求得最优解了，同样地，我们会需要至少10张以上的棋盘格图像，目的是考虑数值稳定性和提高信噪比，得到更高质量的结果。

与此同时，我们在这里引入单应性的概念。在计算机视觉中的单应性被定义为从一个平面到另一个平面的投影映射关系。

我们定义相机标定的单应性矩阵（从物体平面到成像平面）为：

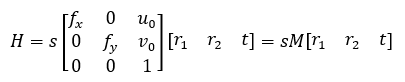
这里引入的s为任意尺度的比例系数。单应性矩阵描述了物体在世界坐标系和像素坐标系之间的相对位置关系（包含了内参和外参）。

若已知标定板上的点在空间和图像上的坐标，即可求解单应性矩阵，且每幅模板对应一个单应矩阵。

1.7标定板

标定算法中我们需要一些可靠的样本点，这些样本点由世界坐标系中的3D点和其在图像上的2D像点组成，用这些2D和3D点对来求解标定参数。

为了构建更高精度的3D和2D点，就需要使用标定板。

1.7.1标定板的基本要求

1）标定板的精度(平整度)：3D点要求是共面的，标定点的坐标精度是准确的。

2）标定板的稳定性：降低温度膨胀系数。标定板的材质温度膨胀系数要尽可能小。

3）标定板的均匀性(背光源)：要求标定板有背光的原因是尽量减少图像受环境光的干扰。

1.7.2pattern设计要求

1）便于特征点提取（如角点或圆心）；

2）特征点的坐标无歧义，比如对于棋盘格这种有规律的pattern，要求棋盘格图像整体的大小不要充满整个图像，比如只占拍摄图像的1/2。

图9：标定板

1.7.3标定板对标定精度的影响

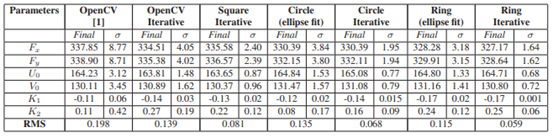
图10：标定精度的对比

一般来讲，圆形(圆环)标定板的提取精度高于棋盘格的提取精度。主要原因是对于棋盘格来讲，边缘位置在实际相机所拍摄的图像来看，受到光的影响和sensor本身噪声影响，所得到的灰度可能会有明暗差别，导致计算棋盘格角点位置的时候会有误差。而圆形或圆环的拟合中，半径多一点或少一点，对于圆心位置的计算影响相对较小。

1.8标定步骤

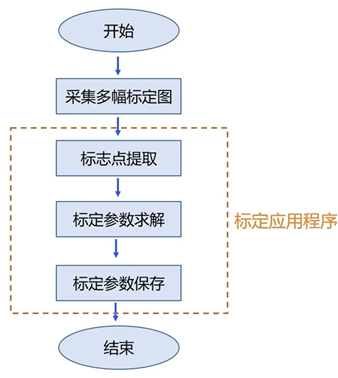
图11：标定步骤

审核编辑：黄飞