

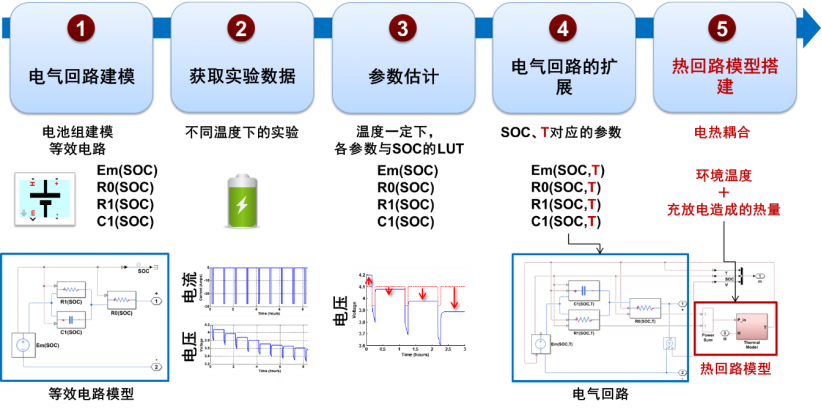
深入探讨电池管理系统开发常见问题
电源/新能源
描述
在开发车辆电池系统时,关键在于精确监测电池的状态,如电压、电流、剩余容量和温度,并优化充放电策略以延长行驶距离,实施故障安全控制以防过充或过放电,以及进行温度管理以保证电池寿命。
利用 Simscape Battery 工具箱,开发者可以创建电池模型,设计电池组,并开发管理系统算法。通过系统级仿真验证电池管理系统 BMS 设计的各项功能,深入了解电池组的动态行为,并探索 BMS 算法的有效性,包括监控电芯电压和温度、估计荷电状态(SOC)和健康状态(SOH)、控制充电曲线、平衡电芯 SOC 等。
但是电池开发工程师在开发过程中,常常遇到一些常见的问题。我们简单总结一下这些共性问题,如下:
答疑专家
楚骏楠
MathWorks 中国区高级应用工程师
主要负责物理建模,系统仿真,以及虚拟车辆建模与优化的解决方案。曾在博格华纳和天合担任仿真工程师。获得上海交通大学机械工程硕士学位。
张香春博士
MathWorks 总部首席应用工程师
专注于电池建模和电池管理系统设计。在 2022 年加入 MathWorks 之前,他在戴森公司担任高级研究经理,负责固态电池的研发工作。他在锂离子电池领域有着 18 年的工作经验,并且他的电池建模方面的研究成果已被引用 3900 次。此外,他还在美国获得了 12 项关于电池的专利(包括电池管理系统算法)。他在清华大学获得了工学学士和硕士学位,并在美国密歇根大学安娜堡分校获得了机械工程博士学位。在密歇根大学期间,他的研究方向是锂离子电池的多尺度多物理场建模,包括力学、热产生和电化学动力学的结合。
◆ ◆ ◆ ◆
问题 1.
我在使用扩展卡尔曼滤波 EKF 做 SOC 估计算法,但是算法结果并不是很准确,是有哪些原因引起的呢?
卡尔曼滤波(Kalman Filter,KF)是一种有效的递归滤波器,用于线性动态系统中的状态估计。它能够基于一系列含有噪声的测量数据,通过预测-更新的过程,估计出系统状态的最优估计值。卡尔曼滤波的基本思想是结合对系统模型的了解(预测)和新的测量数据(更新),以最小化估计的协方差(即估计的不确定性),从而得到一个关于系统状态的最优估计。随着时间累积,方差变小,状态估计值精度提高。
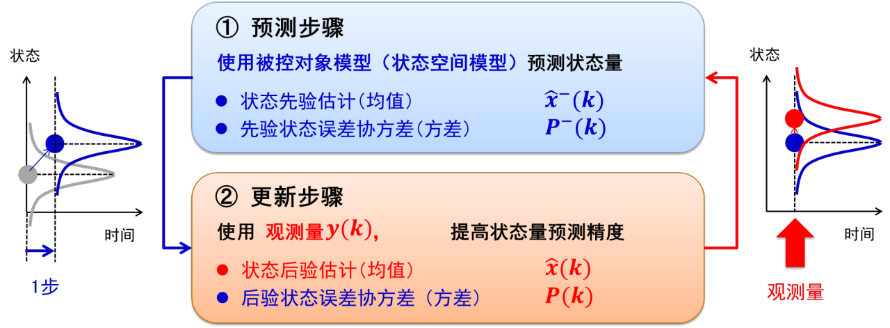
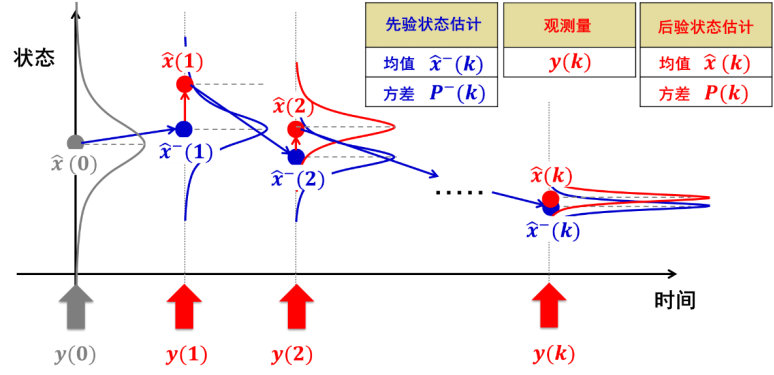
如果用 Simulink 中的方框图表达其原理。如下:
这样的算法我们如何应用在电池荷电状态(State of Charge, SOC)的估计上呢?
在电池管理系统(Battery Management System, BMS)中,荷电状态(State of Charge, SOC)是描述电池剩余电量的关键参数。然而,SOC 不能直接测量,必须通过电池的电压、电流和温度等可测量的参数来估计。
我们使用卡尔曼滤波就是为了估计出电池的 SOC。
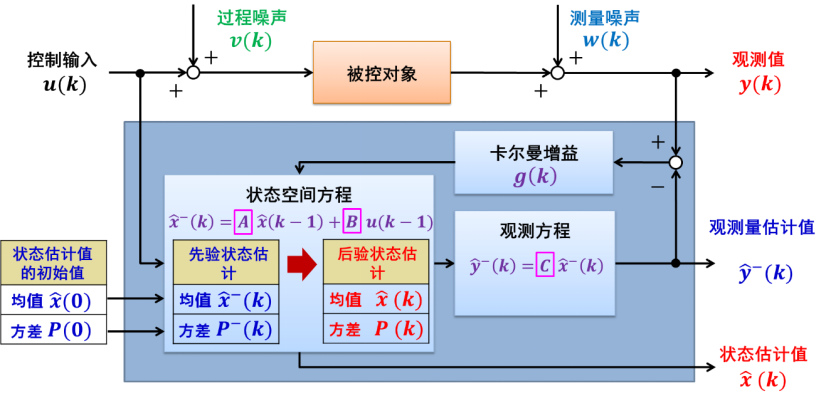
而这里我们需要一个被控对象模型,即电池模型。一般电池模型我们使用的是等效电路模型。
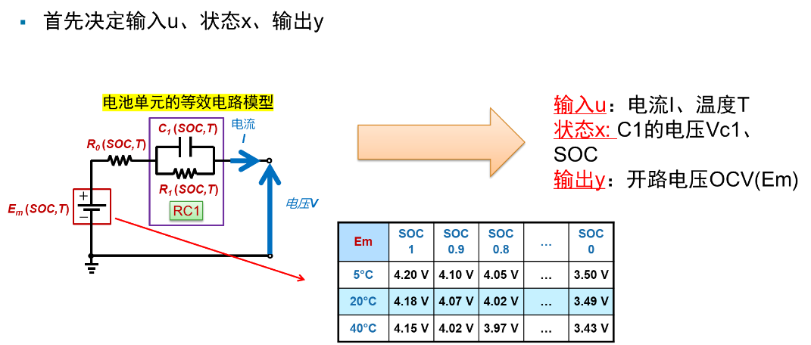
这里我们用状态空间方程表达被控对象即电池的等效电路的模型表达。输入输出和状态均如图表示。
那么,用卡尔曼滤波方法估算电池 SOC 的算法框图就可以表达为以下图示:
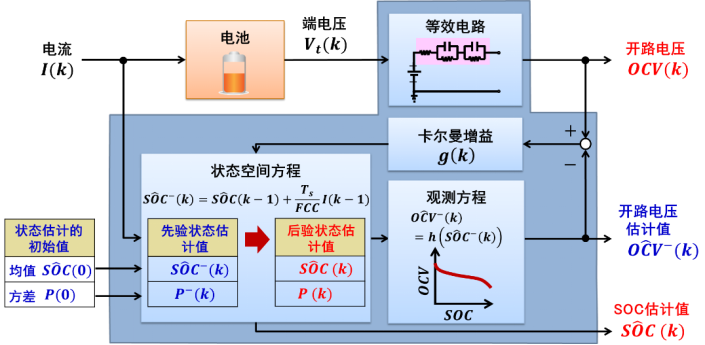
由于等效电路的电池模型是非线性的,因此卡尔曼滤波算法被升级为扩展卡尔曼滤波算法的方法。
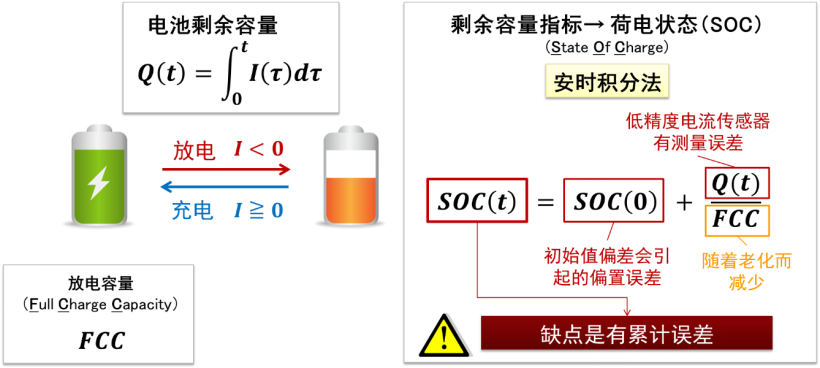
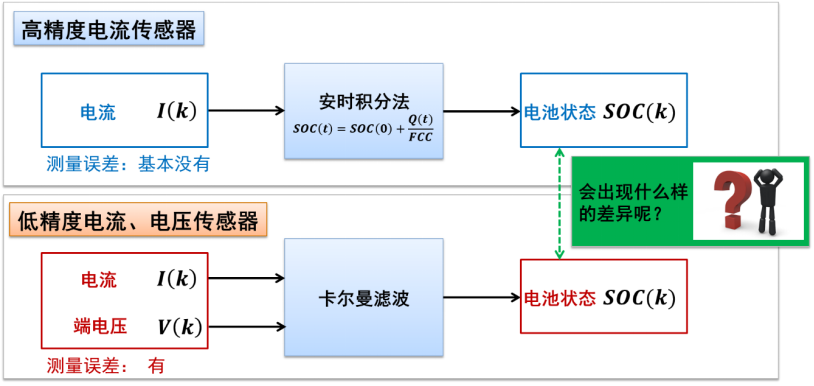
和安时积分法相比较而言,可以做个简单理解。
使用开路电压+安时积分法估算电池 SOC, 只有电流传感器的信息,而使用卡尔曼滤波算法,则是同时使用了电流和电压的信息。因此可以弥补前者的不准确性质。但是,卡尔曼滤波算法的准确性验证仍有需要依靠综合基于高精度传感器的开路电压与安时积分的方法来进行验证。
关于 EKF 的电池 SOC 估计,Simscape Battery 提供了以下模块 。
SOC Estimator (Adaptive Kalman Filter)【1】
SOC Estimator (Adaptive Kalman Filter, Variable Capacity)【2】
SOC Estimator (Kalman Filter)【3】
SOC Estimator (Kalman Filter, Variable Capacity)【4】
基于上述分析,我们可以理解,如果使用 EKF 估算 SOC 不准确,可能存在的原因有以下几点:
模型不准确:EKF 的性能高度依赖于用于描述电池行为的数学模型的准确性。如果模型不能准确反映电池的实际动态行为,包括其非线性特性,那么估计结果将不可避免地出现偏差。
过程噪声和观测噪声的估计不准确:EKF 需要对过程噪声和观测噪声进行估计。如果这些噪声的统计特性(如均值和方差)估计不准确,将直接影响到滤波器的性能。
参数漂移:电池的参数(如内阻)可能会因为老化、温度变化等因素随时间变化。如果 EKF 模型未能适应这些参数的变化,将影响 SOC 估计的准确性。
非线性问题的线性化误差:EKF 通过对非线性模型进行线性化来处理非线性问题。这个线性化过程可能引入误差,尤其是在电池行为高度非线性的情况下。
在处理非线性系统估计问题时, 扩展卡尔曼滤波器(EKF)在设计时通常假设过程噪声和测量噪声是不相关的。这种假设简化了滤波器的设计,但在实际应用中可能不总是成立。
对于最后这两点,我们可以用用无迹卡尔曼滤波 UKF 的算法来解决。无迹卡尔曼滤波器(UKF)在处理过程噪声和测量噪声时采用了不同于 EKF 的方法。UKF 通过选择一组代表性的点(称为 sigma 点)来近似系统状态的概率分布,并将这些点通过系统的非线性函数传递,以此来直接处理非线性问题。这种方法的关键优势之一在于它不需要显式计算雅可比矩阵或海森矩阵(Hessian matrix),从而避免了线性化误差。
但是 UKF 和 EKF 都很难解决电池模型不准确的问题。
问题 2.
既然 EKF 和 UKF 的性能高度依赖于用于描述电池行为的数学模型的准确性,那么如何搭建更准确的等效电路模型呢?如何获取等效电路的参数呢?
脉冲放电实验是用来获取电池等效电路模型(ECM)参数的实验。
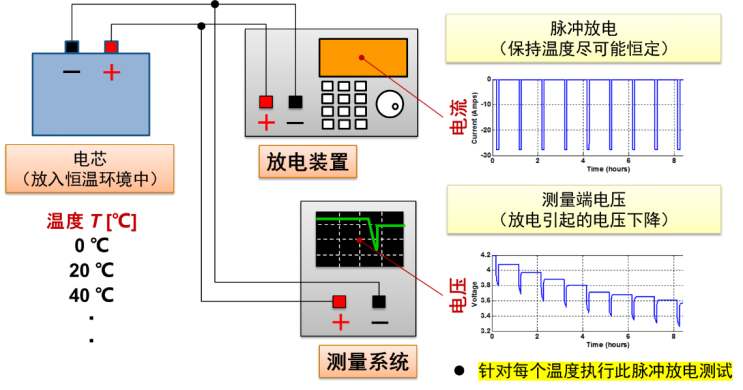
具体实验是对电池施加短时的高电流放电脉冲,通常持续数秒钟,然后让电池恢复一段时间(通常是放电时间的两倍或更长),再施加短时的高电流充电脉冲。通过这种方式,可以模拟电池在实际使用中遇到的快速负载变化。
在不同的 SOC 水平上重复上述实验步骤,以获得电池在其工作范围内的全面性能数据。通过分析脉冲期间和恢复期间的电压响应,可以估计电池的内阻、电容性能以及其他电化学参数
有了脉冲放电实验数据后,就可以对等效电路参数进行参数估计来得到电池模型。
对于脉冲放电实验的参数估计,MATLAB 提供的 Parameter Estimation 工具是一个常用的工具。
(点击播放视频)
Simscape Battery 提供了一个案例,展示了如何通过 MATLAB 脚本的方法使用 HPPC 实验数据进行 ECM 的参数估计。
Characterize Battery Cell for Electric Vehicles【5】
同时,Model Base Calibration 工具箱也提供了电池参数估计的方法,有兴趣的同学可以尝试以下链接。
Calibrate Powertrain Blockset and Simscape Battery Blocks 【6】
当等效电路模型(ECM)参数建模与实际电池不一致时,原因可能较为复杂,涉及多个方面:
模型选择与适用性:ECM 在处理中等电流水平下的电池行为时效果良好,但在高电流或需要深入了解电化学反应的场景下可能不够精确。此时,更复杂的模型,如单粒子模型(SPM)或电化学模型,能更好地描述电池内部的复杂过程。
温度控制的精确性:电池性能与温度密切相关。如果 HPPC 实验中的温度控制不够精确,或电芯实际温度与预期存在偏差,将直接影响模型参数的准确估计。因此,采用加热电偶、温度控制箱等技术保持电池温度的稳定与均匀至关重要。
实验数据质量:高质量的实验数据是确保模型准确性的基础。数据采集过程中的噪声、测量误差或数据处理方法的不当都会影响最终模型参数的准确性。
在进行电池参数估计的实验过程中,确实需要特别注意一些关键问题,以确保数据的准确性和实验的有效性。下面是一些建议:
充放电脉冲不宜过长 :
过长的充放电脉冲可能导致电池过热,影响电池的健康状态和实验数据的准确性。短脉冲可以减少由于电池内部反应导致的热积累,更接近电池的实际工作状态。
电池实验过程中保证电池温度与实验箱一致:
电池实验过程中电池温度的准确性是非常重要的。可以考虑在电池板上增加散热片,使电池获得良好的散热,从而使电池温度与实验箱温度一致。进而保证温度的可靠性。
大规模电池 Pack 实验的数据真实性:
在大规模电池 Pack(包含数百个电芯和多个热电偶)的实验中,确保每个电芯的数据真实准确是非常挑战的。由于电芯之间存在微小的差异,以及热电偶数量有限,可能无法精确反映每个电芯的真实状态。因此尽可能增加测量点,使用更多的热电偶和电压、电流传感器。同时,可以采用分组策略,对 Pack 内的电芯进行分组测量,以提高数据的代表性和准确。
理论上,充电倍率本身不应直接影响等效电路模型(ECM)的参数估计,因为 ECM 的参数(如电阻、电容)旨在描述电池内部的电气特性,这些特性应当是固有的,与充电或放电的速率无关。然而,在实际应用中,充电倍率可能间接影响参数估计的准确性,主要通过以下途径:
非线性效应:电池在不同倍率下的非线性行为可能不易通过简单的 ECM 参数来描述。
这是最关键的一个因素。可以尝试把 ECM 参数(例如电阻和电容)变成与电流相关的查表等参数,或者是使用单粒子电化学模型。
温度变化:高倍率充电可能引起电池温度升高,而 ECM 参数(如内阻)通常与温度有关。
动态行为:高倍率下电池内部的快速反应可能影响其电气特性,从而影响参数估计。
实际操作中需要考虑这些间接影响,并采取措施(如温度控制)来提高模型准确性。
◆ ◆ ◆ ◆
问题 3.
对于锂离子磷酸铁(LiFePO4)的电池有回滞特性。如何来进行电池建模?
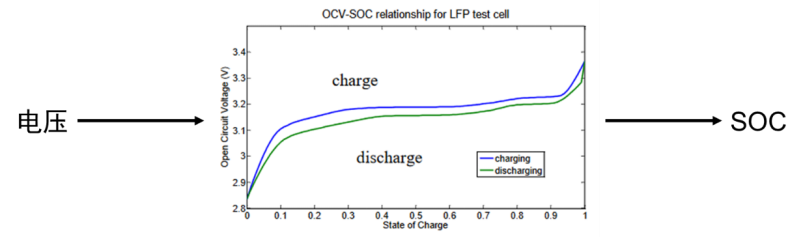
锂离子磷酸铁(LiFePO4,简称 LFP)电池因其独特的化学结构,展现出明显的回滞(Hysteresis)性,即电池的 OCV-SOC 曲线在充电和放电过程中不重合。
OCV 随着电池的先前状态(充电或放电)而变化,这一现象主要由电极活性材料中不同固相的存在、反应路径滞后以及相关的热动力学效应所引起。在充放电过程中,电极活性材料的锂化和脱锂化会导致不同的固相产生,这些固相在电极表面的存在和共存会引起机械应力,进而影响电流流动。
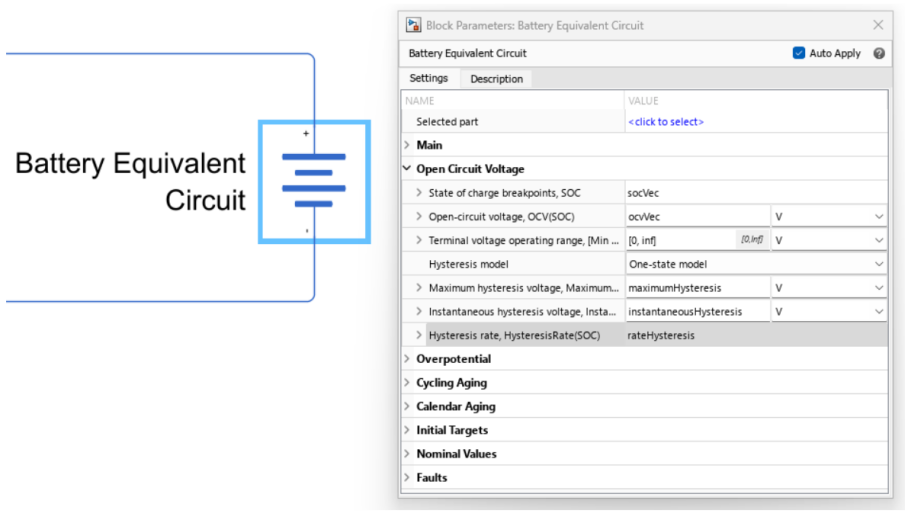
为准确描述LFP电池的回滞特性, Simscape Battery 在 2024a 的版本中引入了新的特性。电池等效电路块采用了 Gregory Plett 提出的单状态滞后模型,它通过引入一个回滞电压项来模拟电池的回滞行为。
电池会根据下面的公式来计算 OCV。
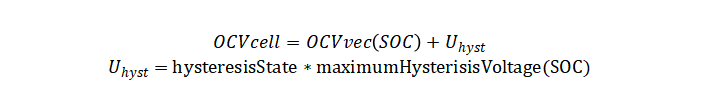
在不考虑电池热模型的情况下,最大滞后电压仅依赖于电池的电荷状态(SOC)。这种情况下,最大滞后电压(maximumHysteresisVoltage(SOC)可以通过充电和放电开路电压(OCV)曲线之间的差异来确定。具体而言,最大滞后电压等于充放电 OCV 曲线之间差异的一半:
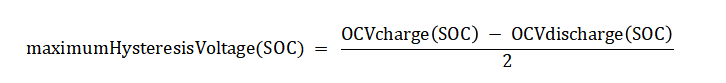
滞后状态 (hysteresisState) 可以通过一阶特征方程来表示,这种方程通常用于描述系统状态随时间变化的动态特性。在电池模型中,考虑滞后效应时,滞后状态的变化可以用以下一阶微分方程来描述:
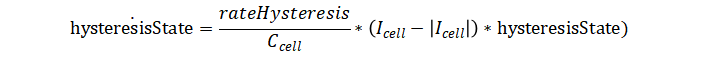
hysteresisState 代表在时间 (t) 的滞后状态。
hysteresisState 是滞后状态随时间的变化率。
rateHysteresis 是一个常数,
Icell 是电池电流,其绝对值的使用确保了变化率始终为正,反映了充电和放电都能影响滞后状态。
Ccell 是是电池容量,以安时(Ah)表示,代表电池的总充电容量。
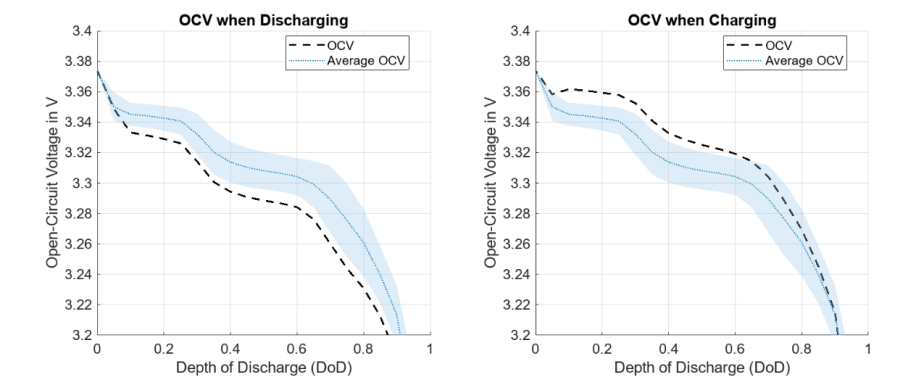
你可以通过下面的链接查看在 Simscape Battery 2024a 版本中电池回滞特性的案例。
Model Voltage Hysteresis in Battery【7】
在这个例子中,你可以打开电池的回滞特性设置。查看器回滞特性的结果绘图如下:
◆ ◆ ◆ ◆
问题 4.
锂离子磷酸铁电池 LFP 的开路电压(OCV)具有明显的平台期特性,这意味着在一定的电荷状态(SOC)范围内,电池的 OCV 变化很小。这个特性给精确建模带来挑战,尤其是在需要准确估计 SOC 的应用中。那么如何应对呢?
高分辨率的 OCV-SOC 曲线:通过精确测量,获得高分辨率的 OCV 与 SOC 之间的关系。这需要在控制环境中对电池进行缓慢充放电,以减小由于电流引起的内阻损失,更准确地测量 OCV。
考虑采用带有迟滞特性的电池模型:把迟滞电压状态作为 EKF SOC 估计的状态量之一。这也可以帮助 SOC 估计的精确性。
电化学模型:相比于简单的等效电路模型(ECM),采用基于电化学原理的模型可以更准确地描述LFP电池的行为,包括 OCV 的平台期特性。电化学模型能够考虑到电池内部的物理和化学过程,但这种模型通常更复杂,计算成本更高。
数据驱动模型:利用机器学习等数据驱动方法来建模 OCV 与 SOC 的关系。通过收集大量的电池充放电数据,可以训练出能够准确预测 OCV 平台期的模型。这种方法可以适应不同工作条件下的电池行为,但需要大量的训练数据。
◆ ◆ ◆ ◆
问题 5.
电池的参数( 容量)可能会因为老化、衰退变化等因素随时间变化。如果 EKF/UKF 模型未能适应这些参数的变化,将影响 SOC 估计的准确性。那么如何来处理进行电池老化特性的估计呢?
电池的健康状态(State of Health, SOH)是衡量电池性能衰减和寿命的重要指标。SOH 估计算法主要是为了评估电池的当前状态与其初始状态相比的变化程度。具体来说,SOH 估计算法主要估计以下几个参数:
容量衰减:电池能够储存和释放的电量随时间减少。
内阻增加:电池内部对电流流动的阻碍增大。
功率衰减:电池单位时间内提供的最大能量降低。
在实际 BMS 的开发中,电池的健康状态(SOH)估计和状态量(如状态的电荷,SOC)估计常常在电池管理系统(BMS)中一起考虑和实现。电池的 SOH 影响其容量和内阻,这直接影响 SOC 的准确估计。反过来,SOC 的变化和充放电行为也会影响电池的老化速度和 SOH。因此,将 SOH 和 SOC 估计结合起来可以提高整体的估计准确性和系统性能。
SOH 估计通常基于以下方法之一或其组合:
容量衰减法:通过比较电池当前容量和初始容量的比值来估计 SOH。
内阻增加法:通过测量电池内阻的变化来估计 SOH。
(SOH 也可以通过使用机器学习算法,根据历史和实时数据来预测电池的SOH)
我们在上文中指出,可以通过 EKF/UKF 估算电池 SOC 状态,电池的内阻状态。那么 SOH 就可以与 SOH 一起估计。
以下是一个案例。
根据容量衰减估计电池运行状况【8】
此示例说明如何使用卡尔曼滤波器估算电池容量和健康状态 (SOH)。电池的初始充电状态 (SOC) 等于 0.5。估算器使用 SOC 的初始条件等于 0.8。电池可持续充电和放电 50 小时。该示例使用扩展卡尔曼滤波器估算电池容量(以安培小时为单位)和 SOC。电池容量的估计误差小于 4%。使用扩展卡尔曼滤波器估算 SOC。使用固定容量时,估计的 SOC 值与真实值不同。为了演示估算器的功能并限制仿真的持续时间,本示例对增加的容量衰减率进行了建模。
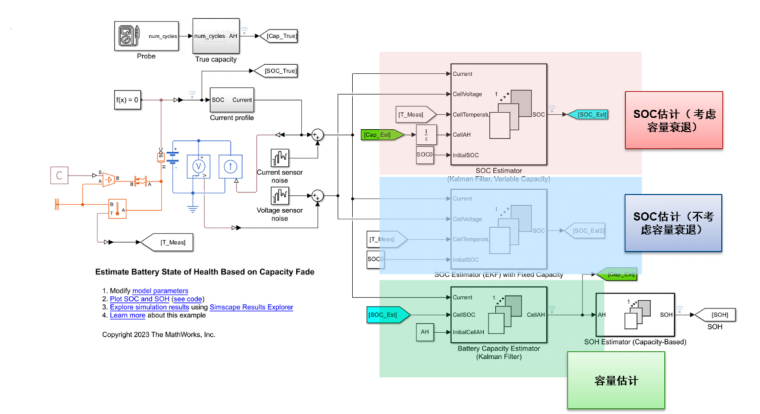
这里的 SOC 估计(考虑容量衰退)模块就是考虑了 SOH 的信息。可以看到,其中输入信号估算的容量 cap_est 是来自于容量衰退模块的计算结果。那么容量衰退模块的算法是有多种多样的。可以是离线的模型,也可以是在线的方法,如卡尔曼滤波的方法。上面这个例子是使用了在线的卡尔曼滤波的算法。
以下是卡尔曼滤波算法对容量估计的计算公式:
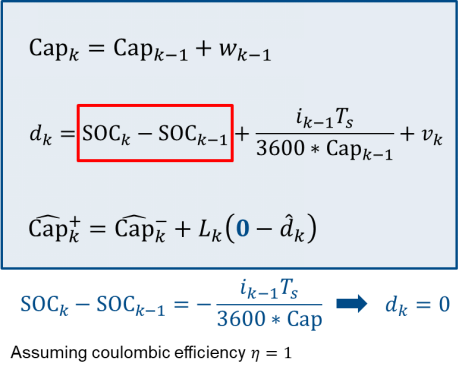
注意,这里的 SOC 不能够由安时积分法来计算出的。
除了使用卡尔曼滤波估算容量,还有一些容量估计算法如 Recursive Least Squares 的算法
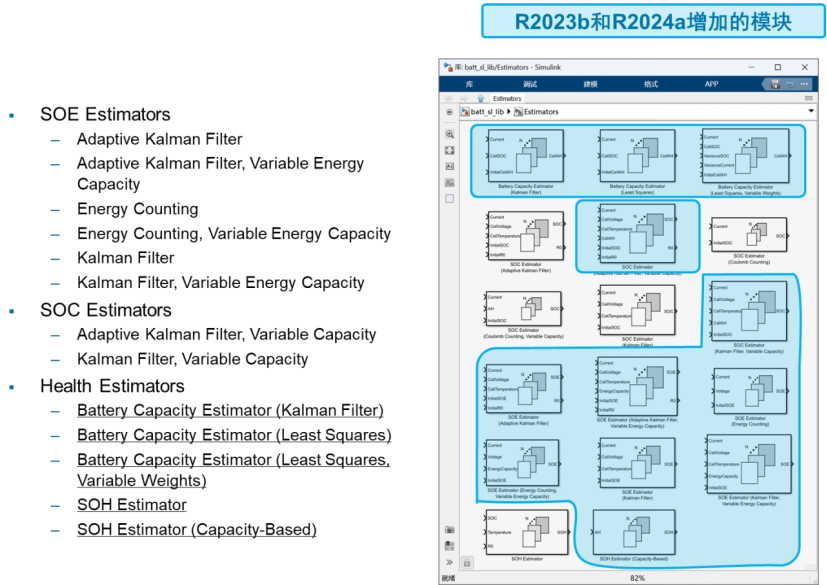
在 2024a 的版本中 Simscape Battery 提供了 Recursive Least Squares 的算法。
Battery capacity estimator using least-squares algorithms - Simulink - MathWorks 中国【9】
2023b 之后 Simscape battery 提供了一系列的电池状态估计的算法,可以帮助用户快速搭建 BMS 系统。
◆ ◆ ◆ ◆
问题 6.
对于等效电路模型(ECM)的参数如何进行验证?
选择一个或多个代表性的驱动循环(drive cycle),这些循环应该能够覆盖电池在预期使用场景下的典型操作条件。对实际电池系统进行测试,收集电池的真实电压、电流等数据。将仿真得到的电池电压与实际测量的电池电压进行对比。计算两者之间的误差,分析误差分布和特点。误差可以用多种方式表达,例如绝对误差、相对误差、均方根误差(RMSE)等。如果误差在 5mV 以内,可以认为是可以接受的。这个标准可能会根据具体应用要求有所不同。如果是用来做 SOC 估计,那么需要理解电压差对 SOC 估计精度的影响。当然,为了增强验证的广泛性和可靠性,可以考虑使用不同的驱动循环进行多次测试和验证,还需要考虑温度带来的影响。
◆ ◆ ◆ ◆
问题 7.
EKF SOC 估计算法发现,换了一些测试场景后不准确了。
除了上文提出的一些原因之外,很重要一点是,EKF 算法的验证必须在被控对象模型的输出信号上加噪声。另外, EKF 协方差调试也是很重要的一个环节。
◆ ◆ ◆ ◆
总结
还有一些行业常见的热点问题,如:
回滞特性参数的获得,如何来设计实验?
在电池老化特性中,需要不仅考虑电池容量的衰减,还要考虑等效电路中,R0, R1 等参数的变化,这也会影响 SOC 的估计,进而对 SOH 算法的计算量带来负担,如何解决 ?
HPPC 实验过于耗时,尤其是等待电池 OCV 稳定的时间,是否有办法用基于路况的电池实验数据进行电池参数的估计呢?
单粒子模型(Single Particle Model)如何搭建及验证?
......
审核编辑:黄飞
-
深入探讨电容的种类和作用2009-11-27 15751
-
Linux的常见问题解答和管理技巧2012-08-19 2677
-
深入探讨DFM在PCB设计中的注意要点2014-10-24 3812
-
【GoKit申请】电动汽车电池管理系统开发2015-11-02 2451
-
stm32 uart硬件实现及深入探讨(单片机通信学习连载4)2021-06-29 3575
-
【视频】 stm32 uart硬件实现及深入探讨32021-09-17 2733
-
【视频】 stm32 uart硬件实现及深入探讨42021-09-22 2906
-
电池驱动调试常见问题有哪些?怎么解决?2021-09-26 1556
-
stm32+bq76940 bms锂电池管理系统开发源码相关资料分享2021-12-30 3304
-
钒电池常见问题解答2009-11-20 1891
-
深入探讨超声波风速风向仪2021-10-27 696
-
深入探讨交通安全统筹信息系统2021-10-29 877
-
动力电池热管理设计研究探讨2022-03-24 3813
-
深入探讨医疗应用的未来发展趋势2022-11-03 565
-
UPS电源使用中的常见问题2024-10-28 1843
全部0条评论

快来发表一下你的评论吧 !

