电源设计指南：拓扑结构（四）

　　一、一种新型独立太阳能发电系统充放电电路拓扑

　　摘要：提出了一种新型充放电电路拓扑及其控制方法，运行灵活，能使光伏系统工作于最佳状态，解决了光伏电池最大功率跟踪和蓄电池最佳充电之间的冲突，提高了系统的效率和可靠性，还能用于其它新能源发电系统。

　　1 引言

　　在独立太阳能发电系统中，为了降低成本、提高效率和可靠性，既要使光伏电池输出最大功率，又要使蓄电池正确充放电，同时还要最大限度地利用所发电能。在目前的光伏系统中，这三者的实现存在矛盾，通常只顾及到一个方面，如只追踪光伏电池最大功率点而放弃蓄电池的最佳充放电，从而限制了系统的效率和寿命。本文将就此问题进行研究探讨，并设计一套高效充放电电路，提出相应的控制策略。

　　2 光伏发电系统充放电所面临的问题

　　2.1 光伏电池的运行特点

　　光伏电池所发功率取决于照射到其表面的太阳辐射量。由于受到当地纬度、经度、时间、空气状态及气象条件等各种因素的影响，实际上在某个地方所能接收到的辐射量时时刻刻都在变化着，偶然的阴影遮蔽也会使输出功率降低，因此，光伏电池所发功率是不断变化的。图1是光伏电池的I—V与P—V特性曲线［1］，图2是其输出变量与温度的关系曲线［1］，可以看出光伏电池的输出最大功率点Pmax、短路电流Isc、开路电压Voc随着辐射强度、环境温度在不停地变化，所以，光伏发电系统要不停地调整，以使光伏电池工作于最大功率点上，但这又同时使得光伏电池的输出电流、电压在不断变化，即输出功率是不断变化的。

　　

　　图1 光伏电池的I—V和P—V特性曲线

　　

　　图2 光伏电池输出变量Pmax，Voc和Isc的相对值（对应于25℃时）与温度的关系

　　2.2 铅酸蓄电池充放电特性

　　目前，免维护铅酸蓄电池作为储能设备，由于维护量小，使用方便等优点，在光伏系统中得到大量应用。在独立太阳能发电系统中，其充放电方式与传统充放电方式不同，既要因夜间带负荷而需要循环充放电，又要在蓄电池快充满时进行浮充。而铅酸蓄电池有其充放电特性，如不按照其充放电特性进行充放电就会造成损坏且效率较低，日常的合理维护措施是必不可少的。目前，在光伏系统中蓄电池是一个薄弱环节，铅酸蓄电池用于光伏系统后寿命缩短，限制了光伏系统的使用寿命，增加了系统的成本和维护费用。研究发现，问题在于蓄电池用于光伏时，充电电流较小和充电时间受限。涓流充电和部分放电容易造成电极上树枝状晶体的生长，导致所谓的记忆效应，蓄电池的充电容量将会降低；强行过充电会使电解液分解，产生气体，造成电解液的丢失［2］。也有人指出，在光伏系统中限制蓄电池寿命的主要因素是蓄电池中的酸分层。在光伏系统中，由于蓄电池一般都处于欠充状态，进一步扩大了蓄电池底部和顶部的硫酸浓度之差，加剧了硫酸盐化和容量损失。同时小电流放电下所形成的PbSO4结晶颗粒粗大，这种结晶溶解困难，最终影响了蓄电池的寿命。在光伏系统中，蓄电池的放电率要比蓄电池应用在其他场合低［3］。

　　光伏电池板比较昂贵，在目前的光伏发电效率下，最大限度地节约所发出的电能是降低成本的一个有效途径，因此，要尽可能地存储和利用所发出的电能，减少光伏电池的空运行。而光伏系统的特点决定了铅酸蓄电池欠充的可能性比较大。目前，在设计光伏系统时，将光伏电池和负载及蓄电池进行固定匹配［4］［5］，同时，存在上面空运行和欠充两个问题，其基本电路结构如图3所示。DC/DC变换器的输出端直接与蓄电池和负载相连，这样做可以避免过充，但却无法解决可能出现的欠充，蓄电池缺乏有效保护，得不到最佳充电，长此下去将导致蓄电池寿命降低，增加了系统维护费用。另外，当光伏电池输出功率较大时，由于负载一般不随意变化，在一定时间段内就可能出现充电功率过大现象，需要启动保护电路限制充电强度，这样势必会造成能源浪费，间接地增加了系统发电成本。同样，由于负载的不确定性，在蓄电池单独供电时就会出现所有电池单元部分放电现象，即蓄电池不能完全放电，这样对蓄电池也是有害的。

　　

　　图3 传统系统电路图

　　3 系统拓扑结构及其控制方案

　　对于上述问题，本文提出了一种新型充放电电路拓扑，采用动态功率跟踪匹配法加以控制。即根据实时功率差，动态地匹配充放电的蓄电池容量（蓄电池个数），也就是动态地变换系统结构，从而实现最佳充放电。系统电路如图4所示，光伏电池经DC/DC变换器与负载和充电电路相连。负载可以变化。充电电路由直流母线和多个蓄电池充电单元组成，每个充放电单元包括双向DC/DC变换电路Hn和蓄电池Bn两部分。双向DC/DC变换电路如图5所示，蓄电池侧为低压侧，能够实现升压和降压［6］。该双向变换电路能实现高低压侧的有效电气隔离，效率高，控制灵活。与传统光伏系统相比，本系统运行灵活，高效可靠，整体寿命得到提高；另一个很大的优点是，容易进行规模扩充，易实现模块化系统集成，能够较好地解决蓄电池在目前的光伏发电系统中所面临的问题。由于蓄电池组容量是可以灵活变化的，所以，需要扩充规模时，只需增加光伏电池板、增加并联的DC/DC变换器数目、增加蓄电池充电单元、更改控制软件程序即可。

　　

　　图4 系统电路图

　　

　　图5 双向DC/DC变换器

　　本系统真正实现了在光伏电池最大功率输出下对蓄电池进行最佳充放电。由图1可看出，光伏电池的最大功率点电压、电流在不同的情况下是变化的。所以，在负载不变的情况下，就需要系统同时调节充电电流来协调光伏电池最大功率跟踪，这样才能实现光伏电池最大功率输出。为了实现光伏电池最大功率输出时对蓄电池进行最佳充放电，负载确定后，控制器同时同方向调整DC/DC变换器和充电器的占空比D，实现最佳充电，也使放电的蓄电池按最佳放电电流放电。在光伏电池运行于最大功率点的前提下，本系统方案包括：

　　1）规定负载的最高限值，保证蓄电池能完成晚间或阴天的单独供电。

　　2）充电时，同时调节光伏工作点跟踪DC/DC变换器和双向DC/DC变换器，由其动态地确定需充电蓄电池数；

　　3）放电时，同样要判断光伏输出功率和负载功率的最大差，以此来确定参加放电的蓄电池数；

　　4）充放电都要维持蓄电池的最佳充放电模式。

　　从图4可以看出，直流母线电压和DC/DC变换器输出电压及负载输入电压相等，总充放电电流ic为DC/DC变换器输出电流与负载电流之差。设DC/DC变换器输出电压uo，输出电流io，输出功率po，负载电流iL，负载功率pL，总充电电流ic，各充放电单元高压侧电流icn，低压侧电流icn′，蓄电池电压uBn，（n为充放电单元的个数），则

　　Po=uoio，PL=uoiL（1）

　　ic=io－iL=icn（2）

　　另外，对于双向DC/DC变换器，由功率守恒得出

　　u1i1=u2i2（3）

　　又占空比D=ton/T，则

　　（4）

　　icn=i1=i2=icn′（5）

　　ic=icn′（6）

　　式中：Dn为第n个充电器的开关占空比，充电时为高压侧开关，放电时为低压侧开关。

　　所以，测得icn′后即可得到icn，得到Ic。这样，控制器实时采集io，uo，iL，icn′，各蓄电池端电压uBn等各数据，得出控制命令和保护措施。

　　系统充放电流程图如图6所示。充放电之前，控制器将满荷电和已被开启充放电的蓄电池从荷电量序列中去掉。然后按照各个蓄电池荷电多少对其余电池进行排列，将荷电量不满且缺量最多的蓄电池Bmax作为第一个充电的电池，然后依次确定充电次序。充电器先从第一个开始充电，即先将第一个充电器与DC/DC变换器一起进行协调控制。当第一个充电器的充电电流达到其蓄电池的最佳充电电流时，转入保护充电模式，对其开始进行恒流充电。在蓄电池端电压达到水解电压（一般为2.3V/单体，高于此值便开始出现电池酸液水解现象）时，转为恒压保护充电，并对过充电压值进行温度补偿，温度补偿系数取－4mV/℃，直至充满。然后按照上述所说方法开启第二个充电器，将其添加到被控制队列中，依次类推。控制器协调各个充电器，使其都尽可能处于最佳充电模式下，并尽可能将先充电的蓄电池充满。放电时与充电相似，实时计算po与pL之差，并以此计算出需放电的蓄电池数nf，计算时以单个蓄电池的最佳放电电流ifb为条件，即icn′=－ifb，nf=Ic/|icn|。放电顺序与充电相同，先从荷电量最大的蓄电池开始放电，以防荷电量小的个体电池完全放电后得不到及时再充。当po与pL之差减小时，以相反的顺序断开充放电单元。当所有蓄电池端电压到达设置的放电终止电压后，立刻停止放电，避免发生过放电。可以看出，放电控制比充电控制相对简单。

　　

　　图6 充放电系统运行流程图

　　4 实验结果

　　为了验证方案的有效性，进行了相关实验。出于冗余考虑，实验用了额定功率3800W的38D1010X400型光伏电池方阵，15只100A·h（20h率），放电深度为60％的蓄电池和一台1000W的负载、一台500W的负载，每3个蓄电池串联为一个单元。其中1000W的负载一直运行，而500W的负载在13时加入，并在15时退出。实验数据见表1，结果表明，在各充放电电流为最佳的情况下，总充放电电流仍能够跟踪光伏电池输出功率的变化。最大功率跟踪和蓄电池充放电情况良好，只有一组蓄电池由于负载变化没有充满。系统既实现了光伏发电最大功率跟踪，又对蓄电池实现了最佳充放电。实验结果与理论分析一致，证明该充放电电路拓扑及其控制方法是可行的。

　　表1 实 验 数 据

　　时间光伏电池输出功率/kW充电电流ic/A

　　5:000－10

　　10:001.757.49

　　13:002.4013.98

　　14:002.257.46

　　15:001.828.19

　　18:000.38－6.19

　　二、电压调整模块（VRM）拓扑综述

　　1引言

　　电压调整模块（VoltageRegulatorModule，VRM）是分布式电源系统（DistributedPowerSystem，DPS）（图1）中的核心部件，它紧靠在需要供电的负载旁，可根据不同负载需要独立调节输出电压，实现具有低电压、大电流、高稳定度输出，高功率密度，快速响应等优良性能的高质量电源系统。

　　根据输入电压的不同，VRM可分为5V、12V、48V输入等不同种类，其相应的电路拓扑有许多不同之处；根据输出和输入间是否隔离，VRM又可分成非隔离型和隔离型两种。目前，VRM较多地采用5V输入电压，但随着芯片负载电流越来越大，今后分布式电源系统中将较多地采用12V或48V总线电压的VRM，经变换输出1V左右电压供给工作站或服务器CPU芯片。

　　本文对近几年提出的VRM拓扑作一综述，对每一种拓扑的结构、原理和主要特点进行简要介绍，同时介绍了交错并联和内置输入滤波器等新的概念和技术。

　　2非隔离型VRM的主要拓扑

　　2？15V输入的VRM拓扑

　　非隔离型VRM的拓扑基本上是在传统的Buck电路基础上变化或改进得到。图2所示为低压VRM中广泛采用的同步整流Buck电路。由于用低压MOSFET（其通态电阻很小，mΩ级）代替了肖特基（Schottky）整流管，因此可大大降低通态损耗，从而提高低压VRM的效率和功率密度。

　　同步整流Buck电路中，滤波电感L一般取得较大，以确保负载变化时Buck电路始终工作于电流连续状态，减小输出电流纹波，从而减小滤波电容值，缩小体积，提高电源的功率密度。但在负载瞬态变化过

　　

　　图1分布式电源系统的一种典型结构［2］

　　

　　图2同步整流Buck电路

　　

　　图3QSW工作波形

　　

　　图4交错连接QSW和消纹波原理

　　（a）交错连接原理图（b）纹波抵消示意图

　　程中，过大的滤波电感限制了能量的传输速度，负载瞬态变化所需要（或产生）的能量几乎全部由滤波电容提供（或吸收）。特别在大电流负载情况下，必须增加滤波电容（一般采用多电容并联以减小ESR和ESL），使电源的体积增大，功率密度降低，也增加了产品的制造成本。由此可见，同步整流Buck电路难以满足今后芯片发展对电源的要求。

　　为了克服同步整流Buck电路在瞬态响应等方面存在的不足，文献［3］提出了一种准方波（Quasi？Square？

　　Wave，QSW）工作方式的拓扑结构。该电路结构与同步整流Buck电路相同，但其输出滤波电感L远远小于同步整流Buck电路中的L值，使QSW电路的瞬态响应时间很短。从工作波形（图3）可见，开关Q1和Q2均可以实现接近零电压开通，使MOSFET的密勒（Miller）效应影响减小，开关损耗和栅极驱动功耗亦减小。但QSW电路也存在着许多问题，首先由于IL的纹波增大，使流过开关管的电流有效值增大，通态损耗增加；其次需要很大的输出滤波电容滤除纹波；再次大的纹波电流亦使磁性元件的损耗增加，使应用QSW拓扑的VRM总体效率低于同步整流Buck电路。

　　为了减少QSW电路输出电流的纹波，同时又能满足快速瞬态响应的要求，文献［3］提出了一种交错并联技术，将多个QSW电路交错并联起来，达到减小输出纹波电流的目的。图4所示为其原理图和纹波抵消原理示意图。图5所示为多相交错并联QSW的消纹波效果比较。

　　从图5可以看到，多相QSW电路交错并联，并合理地选取同步整流开关控制脉冲占空比，可以明显减小输出电流纹波，因此可以用比单相QSW电路中小得多的滤波电容，使电路同时满足静态和瞬态变化的要求；交错并联QSW电路不仅可以减小输出电流纹波，同时也减小了输入电流纹波，使输入滤波电容减小，电容所占体积减小，加上整个电路的效率提高，使VRM功率密度提高成为可能。

　　2？212V输入的VRM电路拓扑对Buck电路而言，其电压转换比M==D，在输出电压一定的条件下，输入电压越高，则D越小。图6所示为同步整流开关控制脉冲占空比D与输出电压VO之间的关系曲线，可见，当输入电压Vin=12V，输出电压VO=1.0V时，占空比D已小于0.1，过小的占空比将给电路工作和性能带来许多问题［1］［4］：

　　（1）引起不对称瞬态响应，卸载（Stepdown）响应性能远差于加载（Stepup）响应性能，如图7所示。在这种不对称工作情况下，只能根据卸载瞬态响应设计输出滤波器等电路参数，给参数的优化带来很大困难。

　　（2）引起变换器整体效率下降。整流开关管Q1为硬关断工作方式，在相等的输出平均电流条件下，12V输入电压时的电流纹波比5V输入电压时大许多

　　

　　图5多相并联QSW的消纹波效果

　　

　　图6Buck电路占空比与电压间的关系

　　D1:Vin=5VD2:Vin=12V

　　

　　图7不对称瞬态响应

　　

　　图8滤波电感电流纹波

　　

　　图9抽头电感Buck电路

　　

　　图10抽头电感Buck等效电路

　　

　　图11抽头电感Buck的工作波形

　　

　　图12不同电路占空比比较

　　M1:n=1M2:n=2M3:n=3

　　（图8），因此关断时的峰值电流也很大；同时，加在Q1两端的关断电压（Vin－Vout）较大，所以输入电压升高，关断损耗增大，使变换器整体效率下降；对同步整流管Q2而言，起决定作用的是通态损耗。在很小的占空比条件下，电流纹波增大，使流过Q2的电流有效值较大，同时由于Q2导通时间很长，所以Q2的通态损耗增大，也使变换器整体效率下降。

　　（3）由于开关管控制脉冲占空比很小，因此多相交错并联所产生的消纹波效果不显著。当输入电压Vin=12V，输出电压VO=1.5V时，占空比D=0.125，从图5可以看到，四相交错并联后的纹波只消除了大约40％。若输出电压进一步降低，则消纹波效果还要差。消纹波的效果越差，意味着为满足瞬态响应性能指标所加的输出滤波电容越大，这是我们所不希望的。

　　存在以上这些问题的主要原因是在输入电压为12V或更高时Buck电路的占空比D过小，因此解决问题的思路就是如何设法增大D。文献［1］和［4］中介绍了一种称为抽头电感Buck电路，其电路、等效电路及其工作波形分别如图9、图10及图11所示。抽头电感Buck电路的电压转换比M==，通过设计抽头电感的匝比“n”，可将开关脉冲占空比D扩展至一个较合理的值。图12为抽头电感Buck电路和传统Buck电路（n=1）的比较，从图中可见，当输入电压Vin=12V，VO=1.5V时，中间抽头电感（n=2）Buck电路的开关脉冲占空比D已扩展至0.222，接近传统Buck电路的2倍。

　　由于开关脉冲占空比D的扩展，使抽头电感Buck电路的许多性能优于传统Buck电路：

　　①适当选取匝比n（n在2与3之间），可获得对

　　

　　图13开关电压应力与匝比的关系

　　

　　图14开关电流应力与匝比的关系

　　

　　图15有源箝位耦合Buck电路及工作波形

　　（a）有源箝位耦合Buck电路（b）工作波形

　　称的瞬态响应性能，有利于效率的优化。

　　②抽头电感Buck电路中，开关Q1的主要损耗仍是其关断损耗，但比传统Buck电路中Q1的损耗小，从而改善了电路的效率。这是因为，Q1电流的纹波较小，在相同的平均输入电流时，Q1的峰值电流较传统Buck电路时小得多，因此减少了Q1的关断损耗。

　　③由于Q1脉冲占空比D的扩展，使交错并联的消纹波效果更加显著。对n=2的抽头电感Buck电路，从图12可见其Q1脉冲占空比D从0.125扩展至0.222，从图5可以读出其纹波消除已达85％，可使输出滤波器更小，损耗更低。

　　当然，抽头电感Buck电路也有其不足之处：

　　①开关Q1的电压应力随n的增大而增大，如图13所示（Vin=12V，VO=1.5V）；由于耦合电感存在漏感，使Q1关断时承受很大的电压尖峰（图11）。因此必须选用较高耐压的MOSFET，而高压MOSFET的通态电阻往往较大，使Q1的通态损耗增大。

　　②开关Q2的电流应力随n的增大而增大，如图14所示（Vin=12V，VO=1.5V，IO=50A），因此不希望取很大的n。

　　从上面分析可以看到，抽头电感Buck电路是12V输入VRM的一个较好的拓扑结构，但由于存在很高的尖峰电压使它难以被实际采用。文献［1］［4］提出了一种有源箝位耦合Buck电路，可以解决上述尖峰电压问题，其电路拓扑和工作波形如图15所示。

　　有源箝位耦合Buck电路的电压转换比M==，当Vin=12V，VO=1.5V，n=2时，D=0.285，比中间抽头电感（n=2）Buck电路（D=0.222）还大，可以进一步改善电路的工作状况；由于箝位电容作用，开关的电压应力被箝位在2（Vin－VO），不随n变化，在12V输入时约为20V，因此可以选用广泛使用的耐压30V的MOSFET作为开关管，使成本和损耗降低；此外，变换器的输入电流是连续的，因此可减小输入滤波器的尺寸。

　　有源箝位耦合Buck电路可以解决抽头电感Buck电路中由于漏电感所产生的尖峰电压问题，同时改善或保持了抽头电感Buck电路的优点，是12V输入VRM较好的一种拓扑，将它与交错并联技术和集成磁（IntegratedMagnetics）技术结合起来，可以实现具有高效率，快速瞬态响应性能的12V输入VRM。但该电路拓扑仍有不足之处，从图15的工作波形可以看到，有源箝位耦合Buck电路的输入电流存在较严重的突变，即某些时段的di/dt较大。因此，必须在有源箝位耦合Buck电路的输入端加滤波电路；同时，该拓扑的输出端也存在电流突变问题，使输出滤波电容的电流有效值增加，效率降低，使用寿命缩短；由于滤波电容等效串联电感（ESL）的存在，输出电流的突变还会引起输出电压的开关噪声。

　　

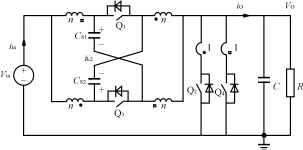
　　图16内置输入滤波器的有源箝位耦合Buck电路

　　

　　图17传统推挽变换器及其主要工作波形

　　（a）传统推挽变换器电路（b）工作波形

　　为了解决上述电流突变问题，文献［5］将内置输入滤波器概念［6］引入至上述有源箝位耦合Buck电路中，提出了改进的有源箝位耦合Buck电路，如图16所示。

　　由于箝位耦合电容CS与漏感所形成的输入滤波器作用，使输入电流和输出电流的变化比较平缓，因此可大大减小外加输入滤波器的尺寸，甚至可以不要外加滤波器而直接利用内置滤波器，从而减少元件的数目。

　　3隔离型VRM的主要拓扑及性能比较

　　随着计算机芯片对电源容量和瞬态响应要求的不断提高，现在被广泛采用的低压（如5V）分布式电源系统将难以满足要求，会逐渐被高压（如48V）分布式电源系统所取代。与低压分布式电源系统相比较，高压分布式电源系统有许多显著优点［7］。

　　从前面的讨论我们知道，低压VRM的电路拓扑很难被应用到高压VRM中。因此高压VRM一般采用具有降压变压器的隔离型电路拓扑，降压变压器起着降压和隔离双重作用。

　　对低压大电流输出VRM而言，副边变换器的功率损耗对整个电路的效率起着主要作用，因此，为提高电路的转换效率，必须努力降低副边变换器的损耗，特别是整流器损耗和变压器的绕组损耗。用同步整流器（低压MOSFET）替换肖特基整流器可以减少整流器损耗；而降低变压器的绕组损耗必须努力减小副边绕组电阻和流过的电流有效值。合理选择绕组和变压器结构可以减小绕组电阻，采用倍流器（Current？Doubler）拓扑可以减小副边电流的有效值［8］。与倍流器输出相适应，变压器原边一般采用具有对称工作方式的推挽变换器、半桥变换器和全桥变换器。

　　图17所示为倍流整流电路（CurrentDoublerRectifier）输出的传统推挽变换器及其主要工作波形。

　　传统推挽变换器的最主要问题是当开关管关断（对Q1而言，t=ton）时，变压器的漏感产生很大的尖峰电压加在管子两端，这与反激变换器的工况相同。为了解决这一问题，文献［7］提出一种新型的推挽正激（Push？PullForward）变换器，其原理图和主要工作波形如图18所示。

　　

　　图18推挽正激变换器及其主要工作波形

　　（a）推挽正激变换器电路（b）工作波形

　　

　　图19改进型推挽正激变换器电路

　　与传统推挽变换器电路相比较，推挽正激变换器电路中引入了一个箝位电容C。在t=0～ton期间，Q1导通，Q2截止，输入电压Vin通过Q1加在绕组1上，而电容C上的电压VC（等于Vin）则加在绕组2上，这时电路就象是两个正激电路并联工作。当Q1关断后，漏感电流使Q2的反并二极管导通续流，而电容C将开关管Q1的端电压箝位在2Vin，因此可以选用额定电压较低的开关管以降低通态损耗。

　　该推挽正激变换器为一个二阶系统，其控制较简单，瞬态响应快；它具有较高的转换效率，而且变压器和电感可以很容易集成在一起［9］，从而大大提高变换器的功率密度。

　　最近，文献［10］将内置输入滤波器概念［6］引入至推挽正激变换器中，提出了改进型推挽正激变换器，如图19所示。这一新拓扑中的开关电流和绕组电流与推挽正激变换器中的相同，但输入电流却几乎是平坦的，这是由于输入电流同时流过两个绕组且有纹波抵消作用，这正是内置输入滤波器的作用［6］。改进型推挽正激变换器的输入滤波器尺寸可以大大减小，或直接利用变压器的漏感作为输入滤波器，且可与其它磁元件集成在一起，使变换器的效率得到大大提高［10］［11］。

　　4结语

　　VRM拓扑有许许多多，每种拓扑有其特点和适用的工况。将准方波工作方式的同步整流Buck电路交错并联，可大大降低输出电流纹波，从而减小输出滤波器的尺寸，同时满足快速动态响应和高效率、高功率密度的要求；通过自耦合电感，可以拓展整流开关管的占空比，改善电路的瞬态响应性能，提高变换器整体转换效率；有源箝位电路可以抑制漏感引起的尖峰电压，减少开关器件的电压应力，同时亦可降低电路损耗；将内置输入滤波器概念引入VRM拓扑中，并利用集成磁技术，可进一步改善电路工况，减小滤波器尺寸。

　　目前VRM拓扑结构改进或新拓扑结构的提出，其基本思想是如何满足VRM高效率、高密度和快速瞬态响应的要求，同时非常重视包括磁集成技术在内的集成封装技术的运用，并将能否采用集成技术作为判断拓扑结构性能优劣的一个重要因素，因此这应成为我们今后研究VRM技术的努力方向。

　　三、SMPS拓扑及转换原理

　　根据电路拓扑的不同，SMPS可以将直流输入电压转换成不同的直流输出电压。实际应用中存在多种拓扑结构，比较常见有三种基本类型，按照功能划分为（参见图2）：降压（buck）、升压（boost）、升/降压（buck-boost或反转）。下面还将讨论图2中所画出的电感充电/放电通道。

　　三种拓扑都包括MOSFET开关、二极管、输出电容和电感。MOSFET是拓扑中的有源受控元件，与控制器（图中没给出）连接，控制器输出脉宽调制（PWM）方波信号驱动MOSFET栅极，控制器件的关断或导通。为使输出电压保持稳定，控制器检测SMPS输出电压，并改变方波信号的占空比（D），即MOSFET在每个开关周期（TS）导通时间。D是方波导通时间和周期的比值（TON/TS），直接影响SMPS的输出电压。两者之间的关系在等式4和等式5给出。

　　MOSFET的导通和关断状态将SMPS电路分为两个阶段：充电阶段和放电阶段，分别表示电感中的能量传递状态（参见图2的环路）。充电期间电感所储存的能量，在放电期间传递给输出负载和电容上。电感充电期间，输出电容为负载供电，维持输出电压稳定。根据拓扑结构不同，能量在电路元件中循环传递，使输出电压维持在适当的值。

　　在每个开关周期，电感是电源到负载能量传输的核心。如果没有电感，MOSFET切换时，SMPS将无法正常工作。电感（L）中所储存的能量（E）取决于电感电流值（I）：

　　

　　在每个开关周期中（图3），电感两端的电压恒定，因此电感中的电流线性变化。根据基尔霍夫电压环路定律，可以得到开关过程中电感两端电压，注意极性以及VIN / VOUT的关系。例如，升压转换器的放电期间，电感两端电压为-（VOUT - VIN）。因为VOUT 》 VIN，所以电感两端电压为负。

　　充电期间，MOSFET导通，二极管反向偏置，能量从电源传递给电感（图2）。由于电感两端电压（VL）为正，电感电流将逐渐上升。同时，输出电容将前一个周期存储的能量传递给负载，以保持输出电压的恒定。

　　

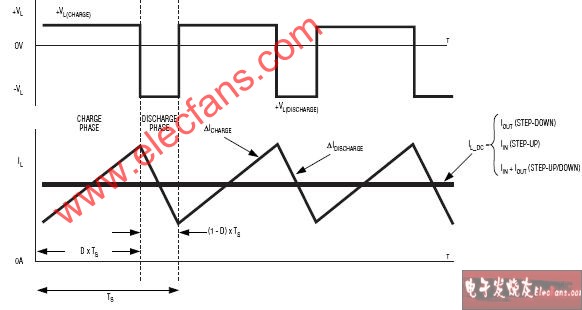
　　图3. 稳态时电感的电压、电流特性。

　　放电期间，MOSFET关断，二极管正向偏置并导通。由于此时电源不再对电感充电，电感两端电压极性反转，并且将能量释放给负载，同时补充输出电容的储能（图2）。放电时，电感电流逐渐下降，放电电流如上述关系式所示。

　　充电/放电周期循环，并保持一个稳定的开关状态。在电路建立稳态的过程中，电感电流逐渐达到其稳定值，该电流是直流电流和电路在两个阶段切换时所产生的交流电流（或电感纹波电流）之和（图3）。直流电流的大小与输出电流成正比，也取决于电感在SMPS拓扑中的位置。纹波电流需要经过SMPS滤波，以获得真正的直流输出。滤波由输出电容完成，它对于交流信号呈现较低的阻抗。不需要的输出纹波电流通过输出电容旁路，并且当电流对地放电时保持电容电荷恒定。因此，输出电容还起到稳定输出电压的作用。实际应用中，输出电容的等效串联电阻（ESR）产生的输出电压纹波与电容的纹波电流成正比。

　　由此可见，能量在电源、电感和输出电容间传递，保持输出电压恒定，为负载供电。那么，通过SMPS间的能量传递如何确定输出电压和输入/输出电压转换比？ 如果能够理解电路作用一个周期性波形的稳态过程，便可以很容易的计算出这些数值。稳态期间，有一个变量在重复周期TS的开始阶段与结束阶段相等。对于电感而言，如上所述，其电流周期性的充电与放电，因此其电流在PWM周期的开始阶段应该与结束阶段相等。这意味着，电感电流在充电过程的变化量（ΔICHARGE）应等于在放电过程的变化量（ΔIDISCHARGE）。建立充电和放电期间电感电流变化的等式，可得到下面的表达式：

　　

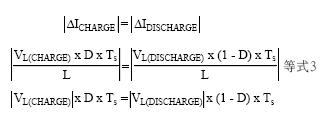
　　简而言之，在不同的工作周期，电感电压和时间的乘积相等。因此，从图2的SMPS电路中，我们可以很容易的得到稳态时的电压和电流转换比。对于降压电路，根据充电电路的基尔霍夫电压环路可得到电感两端的电压为（VIN - VOUT）。同理，放电过程中电路电感两端的电压为-VOUT。根据等式3，可得出电压的转换比为：

　　

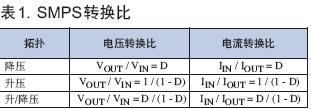
　　从这一系列等式可以看出，降压转换器的输出相比VIN增大了D倍，而输入电流则比负载电流大D倍。表1列举了图2中所示拓扑结构的转换比。有些复杂的拓扑结构可能难以分析，但是利用这个方法解等式3和5可得到全部SMPS的转换比。

　　

　　四、直流开关电源的拓扑结构

　　直流开关电源的拓扑结构

　　开关电源可分为直流开关电源和交流开关电源，是按输出来区分的，交流开关电源输出的是交流电，而直流开关电源输出的是直流电，这里介绍的是直流开关电源。随着相关元器件的发展，直流开关电源以其高效率在很多场合代替线性电源而获得广泛应用。

　　直流开关电源与线性电源相比一般成本较高，但在有些特别场合却更简单和便宜，甚至几乎只能用开关电源，如升压和极性反转等。直流开关电源还可分为隔离的和不隔离的两种，隔离的是采用变压器来实现输入与输出间的电气隔离，变压器还便于实现多路不同电压或多路相同电压的输出。

　　直流开关电源结构复杂，设计和分析都有较特别的一套理论和方法，这里主要介绍6种基本的不隔离的直流开关电源结构形式和其特点，便于依据应用场合来选择使用。

　　理想假定：为便于分析，常假定存在如下理想状态

　　1. 电子器件理想：电子开关管Q和D的导通和关断时间为零，通态电压为零，断态漏电流为零

　　2. 电感和电容均为无损耗的理想储能元件，且开关频率高于LC的谐振频率

　　3. 在一个开关周期内，输入电压Vin保持不变

　　4. 在一个开关周期内，输出电压有很小的纹波，但可认为基本保持不变，其值为Vo

　　5. 不计线路阻抗

　　6. 变换器效率为100%

　　一、Buck变换器：也称降压式变换器，是一种输出电压小于输入电压的单管不隔离直流变换器。

　　

　　图中，Q为开关管，其驱动电压一般为PWM（Pulse width modulation脉宽调制）信号，信号周期为Ts，则信号频率为f=1/Ts，导通时间为Ton，关断时间为Toff，则周期Ts=Ton+Toff，占空比Dy= Ton/Ts。

　　Buck变换器有两种基本工作方式：

　　CCM（Continuous current mode）：电感电流连续模式，输出滤波电感Lf的电流总是大于零

　　DCM（Discontinuous current mode）：电感电流断续模式，在开关管关断期间有一段时间Lf的电流为零

　　1.1 CCM时的基本关系：

　　

　　1.2 DCM时的基本关系：

　　

　　DCM可分为两种典型情况：

　　输入电压Vin不变，输出电压Vo变化，常用作电动机速度控制或充电器对蓄电池的恒流充电

　　输入电压Vin变化，输出电压Vo恒定，即普通开关稳压电源

　　1.3 电感电流临界连续的边界：

　　

　　1.3.1 输入电压恒定不变时：Vin=const

　　

　　可画出Buck变换器在Vin=const时的外特性曲线：

　　

　　图中虚线为电感电流临界连续的边界，内部为电流断续区，外面为电流连续区。

　　理想情况下，在电流断续区输出电压仅由占空比Dy确定。实际电路中，因元器件的非理想化，在电感电流的连续区，Buck变换器的外特性也是下降的，即Io加大，Vo降低。为保持Vo不变，在Io增加时，要适当加大占空比Dy。

　　1.3.2 输出电压恒定不变时：Vo=const

　　

　　可画出Buck变换器在Vo=const时的标幺特性曲线：

　　

　　图中虚线为电感电流临界连续的边界，右上方为电流连续区，左下为电流断续区。

　　在电感电流临界连续时，若加大负载，则进入电流连续工作区；减小负载，则进入电流断续区。

　　若负载不变，减小输入电压Vin，为使Vo不变，应加大Dy，也进入电流连续区。

　　二、Boost变换器：也称升压式变换器，是一种输出电压高于输入电压的单管不隔离直流变换器。

　　

　　开关管Q也为PWM控制方式，但最大占空比Dy必须限制，不允许在Dy=1的状态下工作。电感Lf在输入侧，称为升压电感。Boost变换器也有CCM和DCM两种工作方式。

　　2.1 CCM时的基本关系：

　　Q导通时为电感Lf储能阶段，此时电源不向负载提供能量，负载靠储于电容Cf的能量维持工作；Q关断时，电源和电感共同向负载供电，此时还给电容Cf充电。变换器必须接负载，不然会因能量不断送到负载端而使Vo不断升高而损坏。

　　

　　2.2 DCM时的基本关系：

　　

　　在电流断续时，即使输入电压Vin不变，为了保持输出电压Vo恒定，也要随负载电流的不同来调整占空比Dy。

　　

　　2.3 电感电流临界连续的边界：

　　

　　2.3.1 输入电压恒定不变时：Vin=const

　　

　　2.3.2 输出电压恒定不变时：Vo=const

　　

　　2.3.3 电感电流临界连续的边界曲线：上方为电感电流连续区，下方为断续区

　　

　　电流断续时，开关管Q导通期间存储在电感Lf中的磁能在Q截至期间全部通过二极管D转移到输出端，如果变换器不接负载电阻，或电阻太大，必使Vo不断增加，因此没有电压闭环调节的Boost变换器不能在输出端开路情况下工作。

　　三、Buck/Boost变换器：也称升降压式变换器，是一种输出电压既可低于也可高于输入电压的单管不隔离直流变换器，但其输出电压的极性与输入电压相反。Buck/Boost变换器可看做是Buck变换器和Boost变换器串联而成，合并了开关管。

　　

　　Buck/Boost变换器也有CCM和DCM两种工作方式，开关管Q也为PWM控制方式。

　　3.1 CCM时的基本关系：

　　电感Lf用于储能和转换能量，Q导通时电感Lf储能，负载由电容Cf供电；Q关断时，电感向负载供电。

　　

　　3.2 DCM时的基本关系：

　　

　　3.3 电感电流临界连续的边界：

　　

　　3.3.1 输入电压恒定不变时：Vin=const

　　

　　3.3.2 输出电压恒定不变时：Vo=const

　　

　　3.3.3 电感电流临界连续的边界曲线：上方为电感电流连续区，下方为断续区

　　

　　由图可见，在Vo=const时，如果Dy《0.5，即Vo《Vin，变换器很容易进入电感电流断续区。

　　由于这种变换器的输出电流和电感电流不同，故二者的边界不相同，输出电流Io的边界线在电感电流的下方，因为Io只是电感电流的一部分。

　　四、Cuk变换器：美国加州理工学院Slobodan Cuk提出的对Buck/Boost改进的单管不隔离直流变换器，在输入输出端均有电感，可以显著减小输入和输出电流的脉动，同样是输出电压的极性与输入电压相反，同样是输出电压既可低于也可高于输入电压。Cuk变换器可看做是Boost变换器和Buck变换器串联而成，合并了开关管。

　　

　　开关管Q也为PWM控制方式。Cuk变换器也有CCM和DCM两种工作方式，但不是指电感电流，而是指流过二极管的电流连续或断续。在一个开关周期中开关管Q的截止时间（1-Dy）Ts内，若二极管电流总是大于零，则为电流连续；若二极管电流在一段时间内为零，则为电流断续工作；若二极管电流在t=Ts时刚降为零，则为临界连续工作方式。

　　Cuk变换器中有两个电感，这两个电感之间可以没有耦合，也可以有耦合，耦合电感可进一步减小电流脉动量。

　　分析时增加一个假设：耦合电容C1容量很大，变换器在稳态工作时C1的电压基本保持恒定。

　　4.1 CCM时的基本关系：

　　Cuk变换器中，电源能量经过3次变换才到负载。第一次是Q导通，电感L1储能增长，电能转换为磁储能；第二次是Q截止，L1的磁能转移为C1的电能存储着；第三次是Q导通，C1的电能转移到负载和输出回路的电感L2和电容Cf。实际上，第一、三次两个转换是同时进行的。

　　

　　Cuk变换器中两电感电流增长率和下降率仅与Vin、Vo和自身电感大小有关。电感确定后，两电流增长率只由Vin大小决定，分别为Vin/L1和Vin/L2；下降率只与Vo有关，分别为Vo/L1和Vo/L2。

　　4.2 DCM时的基本关系：

　　

　　4.3 两电感有耦合的Cuk变换器：

　　如果两电感L1和L2绕在同一铁芯上，

　　则两个电感互相耦合，除自感外还有互感M，通常用耦合系数k来表示耦合程度：

　　

　　耦合电感可以进一步减小输入电流和输出电感电流的脉动。

　　五、Zeta变换器：有两个电感和耦合电容的单管不隔离直流变换器，输出电压极性和输入电压相同。Zeta变换器可看做是Buck/Boost变换器和Buck变换器串联而成，合并了开关管。

　　

　　Zeta变换器是电感输出，所以输出电流脉动很小，开关管Q也为PWM控制方式。

　　分析时假设耦合电容C1容量很大，变换器在稳态工作时C1的电压基本保持恒定。

　　5.1 CCM时的基本关系：

　　

　　5.2 DCM时的基本关系：

　　

　　六、Sepic变换器：有两个电感和耦合电容的单管不隔离直流变换器，输出电压极性和输入电压相同。Sepic变换器可看做是Boost变换器和Buck/Boost变换器串联而成，合并了开关管。

　　

　　Sepic变换器是电感输入，所以输入电流脉动很小，开关管Q也为PWM控制方式。

　　分析时假设耦合电容C1容量很大，变换器在稳态工作时C1的电压基本保持恒定。

　　CCM时的基本关系：