深度解析机器学习各大模型原理

大家好，我是花哥。

通俗来说，机器学习模型就是一种数学函数，它能够将输入数据映射到预测输出。更具体地说，机器学习模型就是一种通过学习训练数据，来调整模型参数，以最小化预测输出与真实标签之间的误差的数学函数。

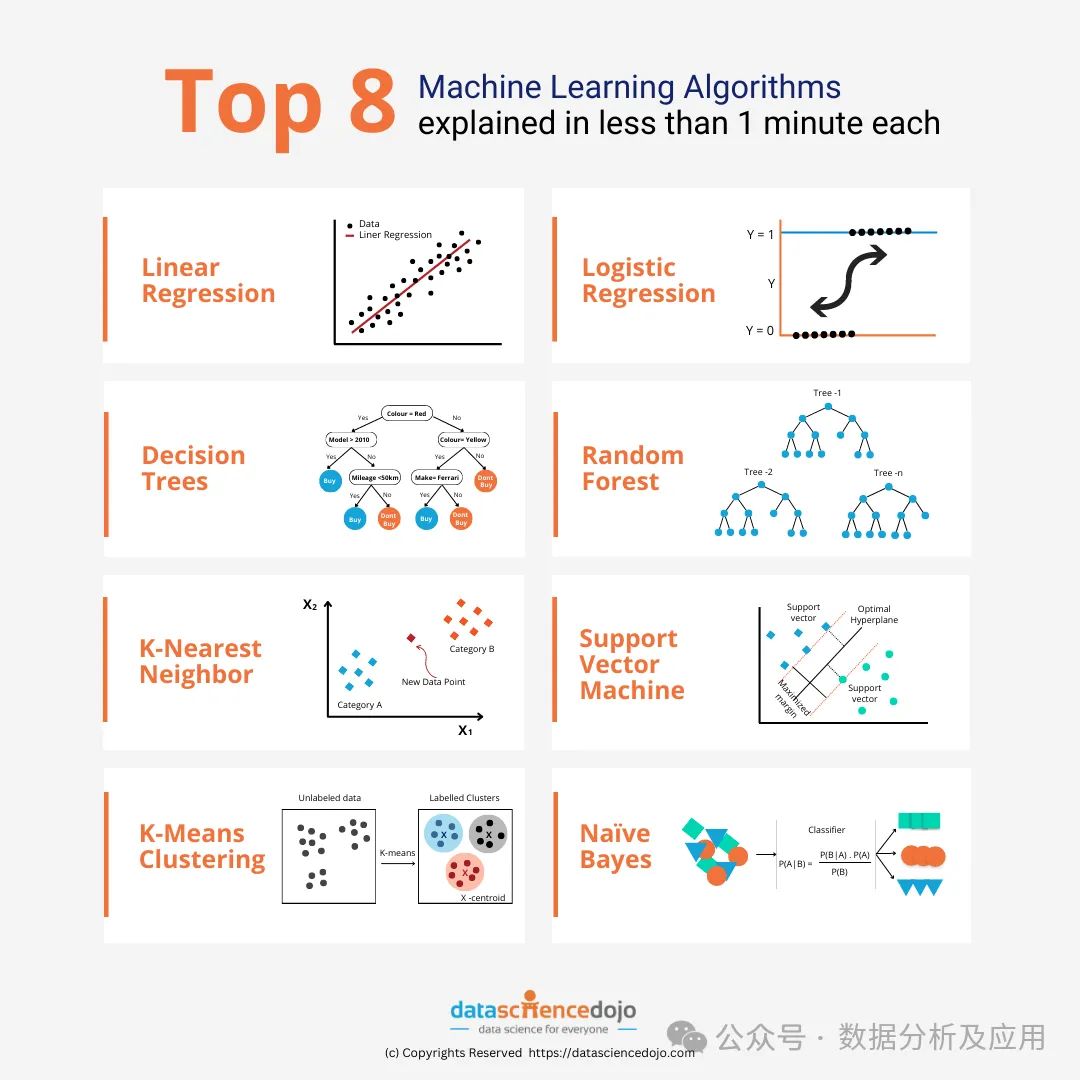
机器学习中的模型有很多种，例如逻辑回归模型、决策树模型、支持向量机模型等，每一种模型都有其适用的数据类型和问题类型。同时，不同模型之间存在着许多共性，或者说有一条隐藏的模型演化的路径。

以联结主义的感知机为例，通过增加感知机的隐藏层数，我们可以将其转化为深度神经网络。而对感知机加入核函数就可以转化为SVM。这一过程可以直观地展示了不同模型之间的内在联系，以及模型间的转化可能。按照相似点，我粗糙（不严谨）地将模型分为如下6个大类，以方便发现基础的共性，逐个深入剖析！

一、神经网络（联结主义）类的模型： 

联结主义类模型是一种模拟人脑神经网络结构和功能的计算模型。其基本单元是神经元，每个神经元接收来自其他神经元的输入，通过调整权重来改变输入对神经元的影响。神经网络是一个黑箱子，通过多层的非线性隐藏层的作用，可以达到万能近似的效果。

代表模型有DNN、SVM、Transformer、LSTM，某些情况下，深度神经网络的最后一层可以看作是一个逻辑回归模型，用于对输入数据进行分类。而支持向量机也可以看作是特殊类型的神经网络，其中只有两层：输入层和输出层，SVM额外地通过核函数实现复杂的非线性转化，达到和深度神经网络类似的效果。如下为经典DNN模型原理解析:

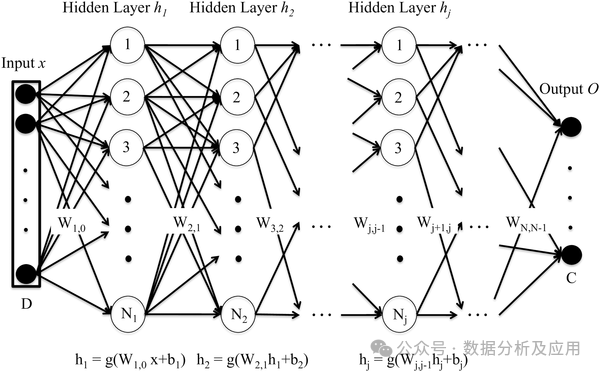
深度神经网络（Deep Neural Network，DNN）由多层神经元组成，通过前向传播过程，将输入数据传递到每一层神经元，经过逐层计算得到输出。每一层神经元都会接收上一层神经元的输出作为输入，并输出到下一层神经元。DNN的训练过程是通过反向传播算法实现的。在训练过程中，计算输出层与真实标签之间的误差，并将误差反向传播到每一层神经元，根据梯度下降算法更新神经元的权重和偏置项。通过反复迭代这个过程，不断优化网络参数，最终使得网络的预测误差最小化。

DNN的优点是强大的特征学习能力：DNN可以自动学习数据的特征，无需手动设计特征。高度非线性及强大的泛化能力。缺点是DNN需要大量的参数，这可能导致过拟合问题。同时DNN的计算量很大，训练时间长。且模型解释性较弱。以下是一个简单的Python代码示例，使用Keras库构建一个深度神经网络模型：

 

 

from keras.models import Sequential  
from keras.layers import Dense  
from keras.optimizers import Adam  
from keras.losses import BinaryCrossentropy  
import numpy as np  


# 构建模型  
model = Sequential()  
model.add(Dense(64, activation='relu', input_shape=(10,))) # 输入层有10个特征  
model.add(Dense(64, activation='relu')) # 隐藏层有64个神经元  
model.add(Dense(1, activation='sigmoid')) # 输出层有1个神经元，使用sigmoid激活函数进行二分类任务  


# 编译模型  
model.compile(optimizer=Adam(lr=0.001), loss=BinaryCrossentropy(), metrics=['accuracy'])  


# 生成模拟数据集  
x_train = np.random.rand(1000, 10) # 1000个样本，每个样本有10个特征  
y_train = np.random.randint(2, size=1000) # 1000个标签，二分类任务  


# 训练模型  
model.fit(x_train, y_train, epochs=10, batch_size=32) # 训练10个轮次，每次使用32个样本进行训练

 

 

二、符号主义类的模型

符号主义类的模型是一种基于逻辑推理的智能模拟方法，其认为人类是一个物理符号系统，计算机也是一个物理符号系统，因此，就可以用计算机的规则库和推理引擎来来模拟人的智能行为，即用计算机的符号操作来模拟人的认知过程（说白了，就是将人类逻辑存入计算机，达成智能执行）。

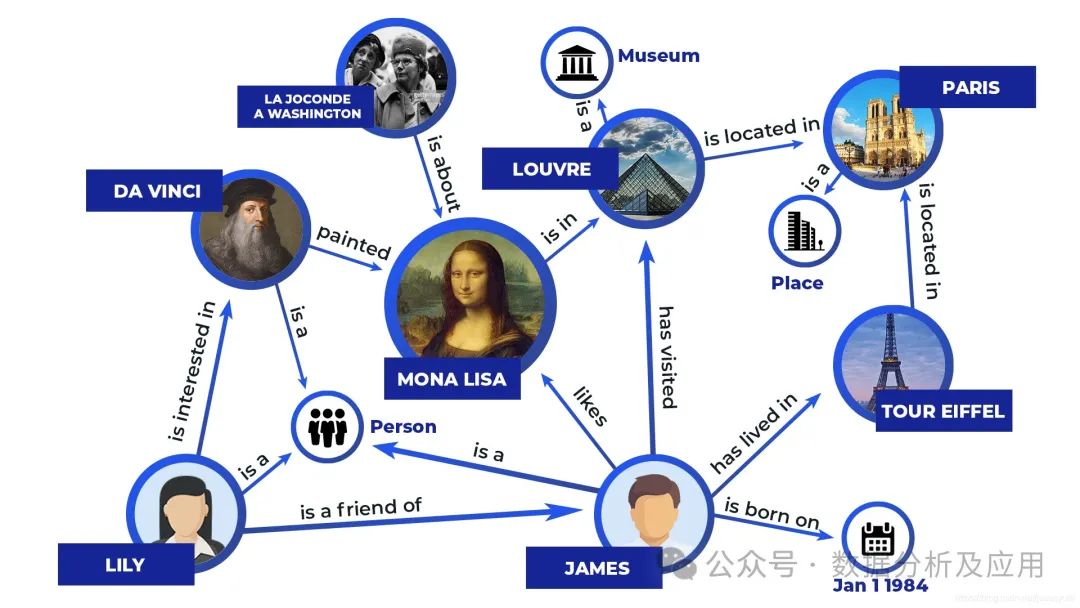
其代表模型有专家系统、知识库、知识图谱，其原理是将信息编码成一组可识别的符号，通过显式的规则来操作符号以产生运算结果。如下专家系统的简单示例：

 

 

# 定义规则库  
rules = [  
    {"name": "rule1", "condition": "sym1 == 'A' and sym2 == 'B'", "action": "result = 'C'"},  
    {"name": "rule2", "condition": "sym1 == 'B' and sym2 == 'C'", "action": "result = 'D'"},  
    {"name": "rule3", "condition": "sym1 == 'A' or sym2 == 'B'", "action": "result = 'E'"},  
]  
  
# 定义推理引擎  
def infer(rules, sym1, sym2):  
    for rule in rules:  
        if rule["condition"] == True:  # 条件为真时执行动作  
            return rule["action"]  
    return None  # 没有满足条件的规则时返回None  
  
# 测试专家系统  
print(infer(rules, 'A', 'B'))  # 输出: C  
print(infer(rules, 'B', 'C'))  # 输出: D  
print(infer(rules, 'A', 'C'))  # 输出: E  
print(infer(rules, 'B', 'B'))  # 输出: E

 

 

三、决策树类的模型

决策树模型是一种非参数的分类和回归方法，它利用树形图表示决策过程。更通俗来讲，树模型的数学描述就是“分段函数”。它利用信息论中的熵理论选择决策树的最佳划分属性，以构建出一棵具有最佳分类性能的决策树。

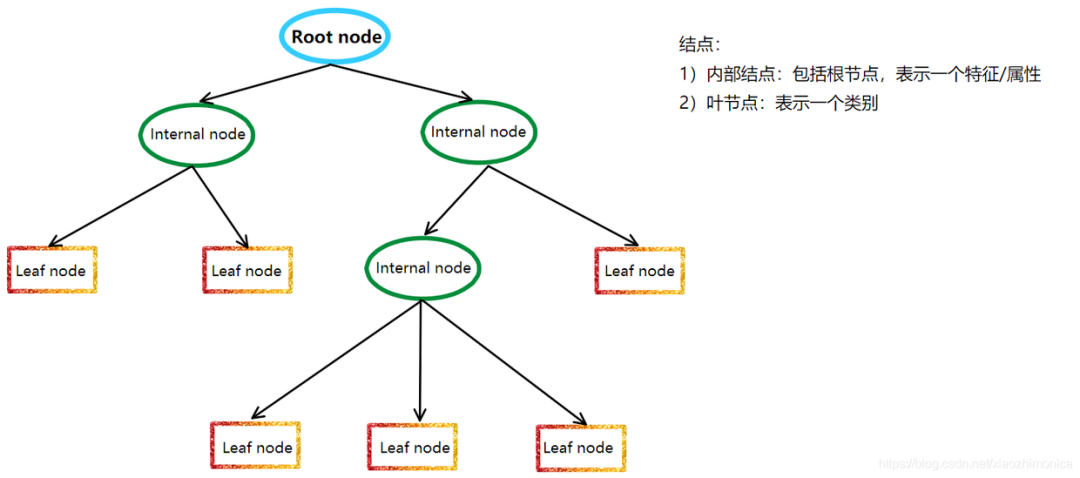
决策树模型的基本原理是递归地将数据集划分成若干个子数据集，直到每个子数据集都属于同一类别或者满足某个停止条件。在划分过程中，决策树模型采用信息增益、信息增益率、基尼指数等指标来评估划分的好坏，以选择最佳的划分属性。

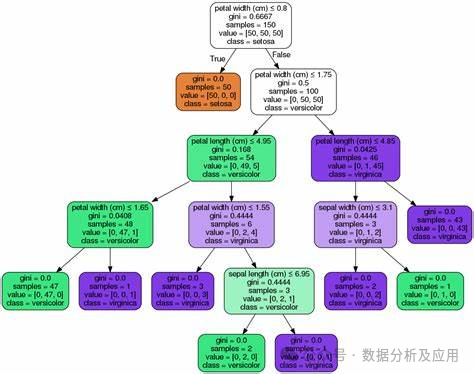
决策树模型的代表模型有很多，其中最著名的有ID3、C4.5、CART等。ID3算法是决策树算法的鼻祖，它采用信息增益来选择最佳划分属性；C4.5算法是ID3算法的改进版，它采用信息增益率来选择最佳划分属性，同时采用剪枝策略来提高决策树的泛化能力；CART算法则是分类和回归树的简称，它采用基尼指数来选择最佳划分属性，并能够处理连续属性和有序属性。

以下是使用Python中的Scikit-learn库实现CART算法的代码示例：

 

 

from sklearn.datasets import load_iris  
from sklearn.model_selection import train_test_split  
from sklearn.tree import DecisionTreeClassifier, plot_tree  
  
# 加载数据集  
iris = load_iris()  
X = iris.data  
y = iris.target  
  
# 划分训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
  
# 构建决策树模型  
clf = DecisionTreeClassifier(criterion='gini')  
clf.fit(X_train, y_train)  
  
# 预测测试集结果  
y_pred = clf.predict(X_test)  
  
# 可视化决策树  
plot_tree(clf)

 

 

四、概率类的模型

概率模型是一种基于概率论的数学模型，用于描述随机现象或事件的分布、发生概率以及它们之间的概率关系。概率模型在各个领域都有广泛的应用，如统计学、经济学、机器学习等。

概率模型的原理基于概率论和统计学的基本原理。它使用概率分布来描述随机变量的分布情况，并使用概率规则来描述事件之间的条件关系。通过这些原理，概率模型可以对随机现象或事件进行定量分析和预测。

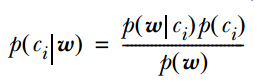
代表模型主要有：朴素贝叶斯分类器、贝叶斯网络、隐马尔可夫模型。其中，朴素贝叶斯分类器和逻辑回归都基于贝叶斯定理，它们都使用概率来表示分类的不确定性。

隐马尔可夫模型和贝叶斯网络都是基于概率的模型，可用于描述随机序列和随机变量之间的关系。

朴素贝叶斯分类器和贝叶斯网络都是基于概率的图模型，可用于描述随机变量之间的概率关系。

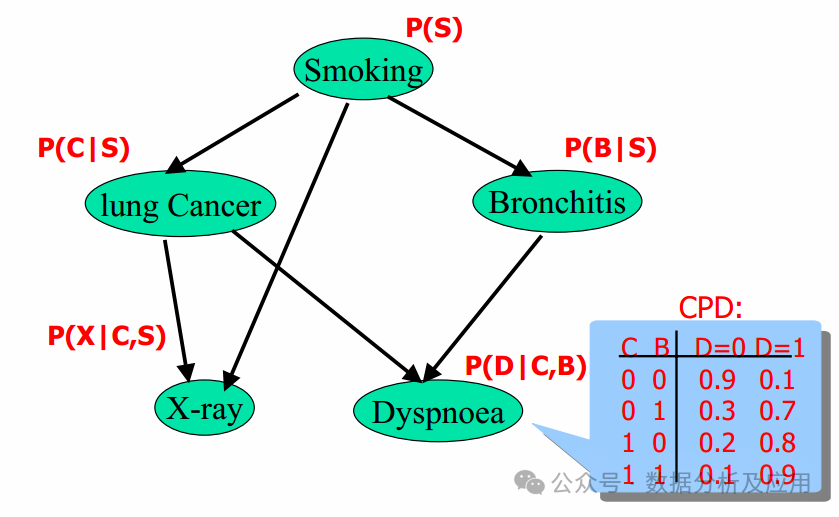
以下是使用Python中的Scikit-learn库实现朴素贝叶斯分类器的代码示例：

 

 

from sklearn.datasets import load_iris  
from sklearn.model_selection import train_test_split  
from sklearn.naive_bayes import GaussianNB  
  
# 加载数据集  
iris = load_iris()  
X = iris.data  
y = iris.target  
  
# 划分训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
  
# 构建朴素贝叶斯分类器模型  
clf = GaussianNB()  
clf.fit(X_train, y_train)  
  
# 预测测试集结果  
y_pred = clf.predict(X_test)

 

 

五、近邻类的模型

近邻类模型（本来想命名为距离类模型，但是距离类的定义就比较宽泛了）是一种非参数的分类和回归方法，它基于实例的学习不需要明确的训练和测试集的划分。它通过测量不同数据点之间的距离来决定数据的相似性。

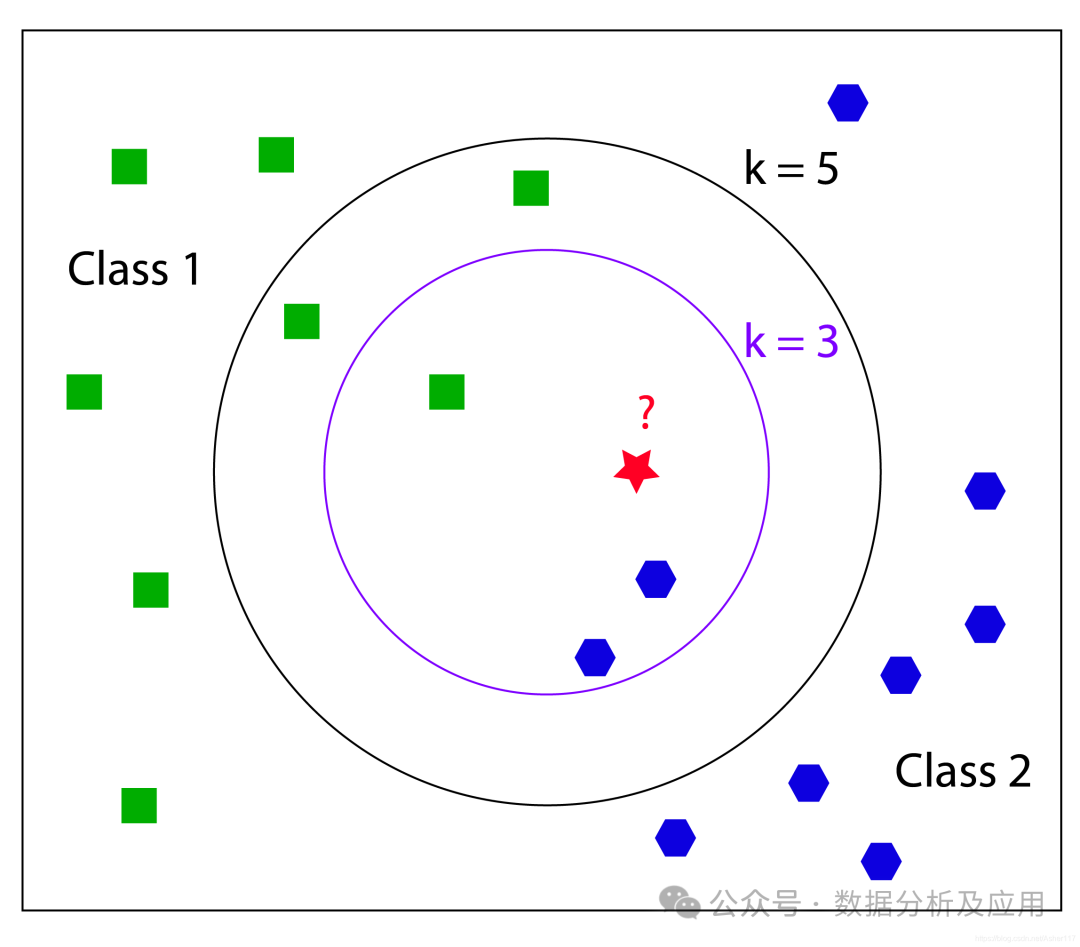
以KNN算法为例，其核心思想是，如果一个样本在特征空间中的 k 个最接近的训练样本中的大多数属于某一个类别，则该样本也属于这个类别。KNN算法基于实例的学习不需要明确的训练和测试集的划分，而是通过测量不同数据点之间的距离来决定数据的相似性。

代表模型有：k-近邻算法（k-Nearest Neighbors，KNN）、半径搜索（Radius Search）、K-means、权重KNN、多级分类KNN（Multi-level Classification KNN）、近似最近邻算法（Approximate Nearest Neighbor， ANN）

近邻模型基于相似的原理，即通过测量不同数据点之间的距离来决定数据的相似性。

除了最基础的KNN算法外，其他变种如权重KNN和多级分类KNN都在基础算法上进行了改进，以更好地适应不同的分类问题。

近似最近邻算法（ANN）是一种通过牺牲精度来换取时间和空间的方式，从大量样本中获取最近邻的方法。ANN算法通过降低存储空间和提高查找效率来处理大规模数据集。它通过“近似”的方法来减少搜索时间，这种方法允许在搜索过程中存在少量误差。

以下是使用Python中的Scikit-learn库实现KNN算法的代码示例：

 

 

from sklearn.datasets import load_iris  
from sklearn.model_selection import train_test_split  
from sklearn.neighbors import KNeighborsClassifier  
  
# 加载数据集  
iris = load_iris()  
X = iris.data  
y = iris.target  
  
# 划分训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
  
# 构建KNN分类器模型  
knn = KNeighborsClassifier(n_neighbors=3)  
knn.fit(X_train, y_train)  
  
# 预测测试集结果  
y_pred = knn.predict(X_test)

 

 

六、集成学习类的模型

集成学习（Ensemble Learning）不仅仅是一类的模型，更是一种多模型融合的思想，通过将多个学习器的预测结果进行合并，以提高整体的预测精度和稳定性。在实际应用中，集成学习无疑是数据挖掘的神器！

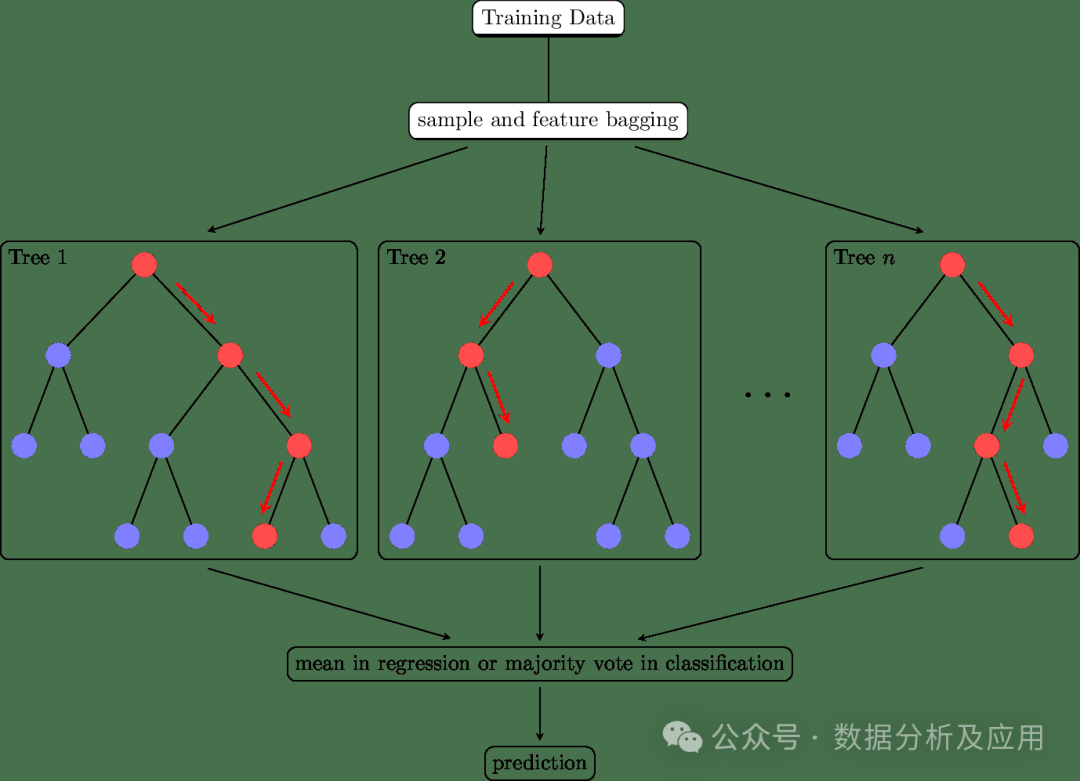
集成学习的核心思想是通过集成多个基学习器来提高整体的预测性能。具体来说，通过将多个学习器的预测结果进行合并，可以减少单一学习器的过拟合和欠拟合问题，提高模型的泛化能力。同时，通过引入多样性（如不同的基学习器、不同的训练数据等），可以进一步提高模型的性能。常用的集成学习方法有：

Bagging是一种通过引入多样性和减少方差来提高模型稳定性和泛化能力的集成学习方法。它可以应用于任何分类或回归算法。

Boosting是一种通过引入多样性和改变基学习器的重要性来提高模型性能的集成学习方法。它也是一种可以应用于任何分类或回归算法的通用技术。

stack堆叠是一种更高级的集成学习方法，它将不同的基学习器组合成一个层次结构，并通过一个元学习器对它们进行整合。堆叠可以用于分类或回归问题，并通常用于提高模型的泛化能力。

集成学习代表模型有：随机森林、孤立森林、GBDT、Adaboost、Xgboost等。以下是使用Python中的Scikit-learn库实现随机森林算法的代码示例：

 

 

from sklearn.ensemble import RandomForestClassifier  
from sklearn.datasets import load_iris  
from sklearn.model_selection import train_test_split  
  
# 加载数据集  
iris = load_iris()  
X = iris.data  
y = iris.target  
  
# 划分训练集和测试集  
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
  
# 构建随机森林分类器模型  
clf = RandomForestClassifier(n_estimators=100, random_state=42)  
clf.fit(X_train, y_train)  
  
# 预测测试集结果  
y_pred = clf.predict(X_test)

 

 

综上，我们通过将相似原理的模型归纳为各种类别，以此逐个类别地探索其原理，可以更为系统全面地了解模型的原理及联系。

审核编辑：黄飞