人工神经元实时谐波电流数字检测

　　采用滤波器对畸变电流进行滤波和补偿是解决电网谐波和无功干扰的重要手段，也是消除谐波电流对电网影响的最终措施。有源电力滤波器原理图如图1.1所示,有源滤波器向电网注入与负载谐波电流幅值相等的反相谐波电流ic以抵消原有谐波电流，使电源电流is近似为正弦波。谐波检测电路检测的结果是控制电路的输入，从而决定控制电路的输出，而控制电路的输出又决定了有源电力滤波器的输出补偿电流ic,所以有源电力滤波器补偿电流大小、方向、相位及精度很大程度取决于谐波的检测电路。如果检测电路具有实时性好、精度高、误差小等优点，有源电力滤波器的补偿就会较好。否则，有源电力滤波器补偿电流ic要么大于谐波电流，出现过补偿，从而成为又一谐波源;要么ic小于谐波电流，出现欠补偿。谐波检测对有源电力滤波器补偿起很大的决定性作用，如果要求有源电力滤波器的补偿效果好，必须使谐波检测电路检测电路具有实时性好、精度高、误差小等优点，实时性和连续性均有赖于无功电流的检测的实时性和精度，所以有必要深入研究谐波测量电路。

　　

 

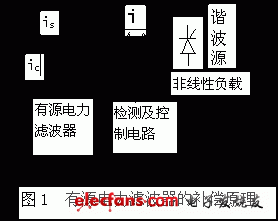
　　传统的检测方法有Fryze时域分解、槽形滤波器、基于频域的FFT变换法、用于不平衡三相系统的同步检测法，这些方法主要的缺点是1)时延较大;2)难以实现，如槽形滤波器法;3)当电压畸变时将带来较大的误差。近来提出的P-Q法[3]的缺点是在电源畸变大时，含有畸变的电压，使计算的iaf、ibf、icf也含有谐波，而、由各次谐波电流成分组成，因而该法在谐波较大的情况下误差较大。

　　1 基于自适应干扰对消原理的谐波检测方法

　　自适应干扰对消理论技术是近年来得到广泛使用的信号处理技术[4、5、6]。由于它能够通过不断的自我学习和自我调整使系统处于最佳状态，所以在不同的领域得到应用。

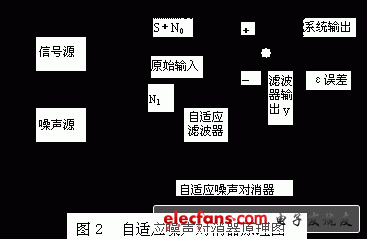
　　自适应干扰对消原理是：系统有两个输入端——原始输入和参考输入端(原理图参见图2)。系统的原始输入是信号S和加性噪声N0，S和N0不相关。系统的参考输入端是噪声N1与N0相关但与S不相关。N1经过自适应滤波器处理后与原始输入信号相减，系统经过自适应算法的调整，使系统平均输出功率最小，也就是使N1逼近N0，然后减去原始输入中的N0成分，以达到抵消干扰的目的。可以证明：此时系统的输出ε是信号S在最小均方准则下的最佳估计[7]。

　　谐波检测的目的为了实时地提取畸变电流中的谐波和无功电流。如果把基波电压作为参考输入，而非线性负荷电流作为原始输入。与上述情况相似，通过自适应滤波器出来后的参考输入，最终被迫在幅度和相位上逼近电压原始输入中的基波信号，然后从负载电流中减去这基波分量，结果为系统的输出—所有谐波分量和无功之和，就达到检测谐波和无功的目的了。同理，将基波及与基波的正交函数作为输入，就达到检测谐波电流的目的了。

　　

 

　　2 基于人工神经元自适应的谐波检测方法

　　2.1 无时延的人工神经元谐波和无功检测方法

　　单个人工神经元有一定的处理、计算及映射能力，具有自适应和自学习能力，所以上述的自适应滤波器实现的检测系统，也可以用神经元代替，如果性能较好、学习算法简单，由于神经元结构简单，就能达到快速检测谐波的目的。

　　无时延的谐波检测方法可以检测广义无功电流ib(也就是谐波电流ih及无功电流i1q之和)。无时延自适应神经元谐波及无功电流检测方法的框图见图3。

　　2.2 正交函数输入的神经元自适应谐波检测方法

　　这种方法实际上是有时延的神经元谐波检测方法的特例，也就是将时延设定为-T/4，将m设定为1，而形成两个正交的函数作为参考输入，在实现时把这种方法的时延设定为-T/4，它的实现可以取保存在内存的现在时刻以前四分之一周期的电压采样作为余弦函数。如果在电压频率较恒定的情况下(一般电压畸变很小)，可以先计算出采样数目差，然后用现时刻的采样电压和保存在内存的现在时刻以前计算出的采样电压作为参考输入，那么，参考输入向量为：

　　X(k)=[u(k),u(k+T/4)] (1)

　　在电压频率变化不大，在这里只要根据采样的频率和基波平移900相角所需要时间来计算现时刻以前的时刻：

　　T/4¸T′=1/(50´4)¸(1/2000)=10 (2)

　　式中T为频率固定的电压的周期，T′为采样周期。图4为正交函数输入的电压频率固定的神经元自适应谐波检测方法的框图。

　　2.3 基于人工神经元自适应的谐波检测方法的实现

　　在这里，神经元为离散型输入，这里权值w为模拟量，在区间[-1,1]之间取随机值，采样周期取2000HZ，初始阀值为零,学习率先选h=0.11，以后再根据实验结果进行调整，惯性系数为a=0.1。

　　其中数组x(120)，y(120)分别为电压、电流采样后保存在PC机内存的数值。

　　3 实验结果

　　本实验将Pentium的CPU、主频率为100MHz、内存为8MB的PC兼容机，作为数据计算的硬件，将PCL-818L多功能卡作为集数据采样、A/D转换、数据传输硬件。由于单位方波具有代表性，本文使用单位方波非线性负载电流做实验。

　　3.1 无时延的人工神经元谐波和无功检测方法实验结果

　　3.1.1单位方波非线性负载电流的实验结果

　　通过大量地实验研究，发现对于不同的h值，计算的结果与实验结果的误差不同，当h=0.04，a=0.01时，ir趋近i1p，id逼近ic，误差也很小，详见图5。图5是初始权值为在-1到1的随机值,初始阀值为零。利用电源电压作为参考输入，采样频率为2000Hz(下面实验都为2000Hz)对幅值为1的方波非线性负载电流计算它的谐波及无功电流的实验结果。为了了解及验证实验的结果，在图中同时画了ic(检测值)和i1p(由理论计算得到的)的波形，图5.b为从图5.a中分

　　

 

　　离出来的有功电流，谐波及无功电流的波形示于图5.c中，图5.d为检测出的谐波及无功电流与理论值之间的误差。由图5可以明显地看出在第一个周期内无论是有功电流还是谐波及无功电流都与理论值有一定的差别，大约在第二个周期它们的差别就不太大了，计算有功电流ir逼近其理论值i1p、而计算谐波及无功电流id趋近于理论广义无功电流ic，它们的误差在第二周期以后仅仅在0.1A以下，约占总电流的5%左右，从上述两种结果可以看出，神经元的学习率h合理选择对神经元的学习收敛具有较大的影响，合理的学习率h选择可以加速收敛。

　　3.1.2 频率变化的方波非线性负载电流的实验结果

　　详见图6。该结果是在h=0.04，a=0.01条件下，从新启动系统，在第三个周期改变负载电流的频率，从50Hz变为55Hz。从图6.b、6.c及6.d中可以清楚地看出:频率对无延迟神经元谐波检测系统来说影响不大，也就是说，该方法对频率的变化有较强的适应性，能够几乎完全跟随频率的变化，有功电流、谐波及无功电流都能随着频率的变化而变化，误差率没有因为频率改变而变化。

　　

 

　　图5 h=0.04时无时延谐波检测实验结果

　　

 

　　图6频率变化时无时延谐波检测结果

　　3.2正交函数输入的神经元自适应谐波检测方法

　　3.2.2 负载电流变化的方波检测结果

　　结果详见图7。从图7.b和图7.c中可以看出，当负载电流从1A突变到0.5A时，大约经过一个周期的适应，计算基波电流ir和谐波电流id逼近它们的理论值i1、ih，说明这种方法对负载电流变化的跟随性也比较好。从误差曲线图7.d看，在负载电流变化的第二周期，误差就小于0.1A了。

　　3.2.3 频率变化的方波非线性负载电流检测结果

　　从图8中可以清楚地看出，正交函数作为参考输入的神经元自适应谐波检测系统对频率变化不“敏感”，在频率变化时，不会产生突变，能够迅速跟随频率变化，在图8.b、8.c中计算基波电流ir和谐波电流id与紧密地随着它们的理论电流i1、ic变化而变化。因此，系统始终具有对被检测的负载电流频率自动跟随能力。

　　

 

　　图7 方波非线性负载变化时检测结果

　　

 

　　图8 频率变化方波负载电流检测结果

　　4 结论

　　提出的方法对负载电流的频率变化及幅值变化具有自适应性，证明了所提出的方法具有良好的实时性。从而本文所提出的方法确实可行。