时域时钟抖动分析(上)

　　本系列文章共有三部分，“第 1 部分”重点介绍如何准确地估算某个时钟源的抖动，以及如何将其与 ADC 的孔径抖动组合。在“第 2 部分”中，该组合抖动将用于计算 ADC 的 SRN，然后将其与实际测量结果对比。“第 3 部分”将介绍如何通过改善 ADC 的孔径抖动来进一步增加 ADC 的 SNR，并会重点介绍时钟信号转换速率的优化。

　　采样过程回顾

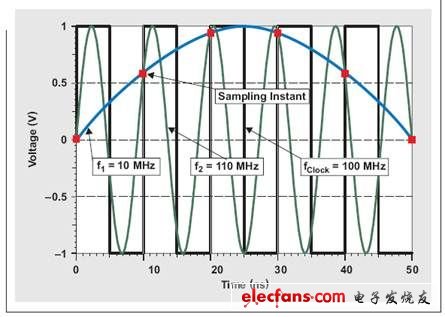
　　根据 Nyquist-Shannon 采样定理，如果以至少两倍于其最大频率的速率来对原始输入信号采样，则其可以得到完全重建。假设以 100 MSPS 的速率对高达 10MHz 的输入信号采样，则不管该信号是位于 1 到 10MHz 的基带(首个Nyquist 区域)，还是在 100 到 110MHz 的更高 Nyquist 区域内欠采样，都没关系(请参见图 1)。在更高(第二个、第三个等)Nyquist 区域中采样，一般被称作欠采样或次采样。然而，在 ADC 前面要求使用抗混叠过滤，以对理想 Nyquist 区域采样，同时避免重建原始信号过程中产生干扰。

　　图 1 100MSPS 采样的两个输入信号显示了混叠带来的相同采样点

　　

 

　　时域抖动

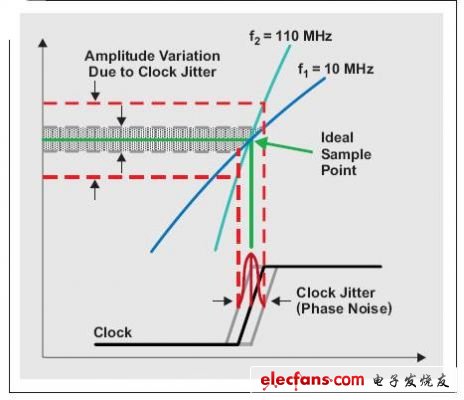
　　仔细观察某个采样点，可以看到计时不准(时钟抖动或时钟相位噪声)是如何形成振幅变化的。由于高 Nyquist 区域(例如，f1 = 10 MHz 到 f2 = 110 MHz)欠采样带来输入频率的增加，固定数量的时钟抖动自理想采样点产生更大数量的振幅偏差(噪声)。另外，图 2 表明时钟信号自身转换速率对采样时间的变化产生了影响。转换速率决定了时钟信号通过零交叉点的快慢。换句话说，转换速率直接影响 ADC 中时钟电路的触发阈值。

　　图 2 时钟抖动形成更多快速输入信号振幅误差

　　

 

　　如果 ADC 的内部时钟缓冲器上存在固定数量的热噪声，则转换速率也转换为计时不准，从而降低了 ADC 的固有窗口抖动。如图 3 所示，窗口抖动与时钟抖动(相位噪声)没有一点关系，但是这两种抖动分量在采样时间组合在一起。图 3 还表明窗口抖动随转换速率降低而增加。转换速率一般直接取决于时钟振幅。

　　

 

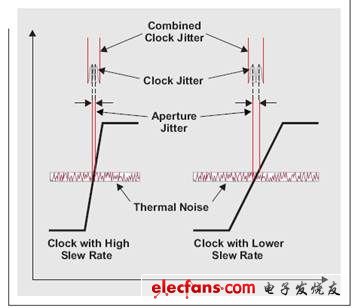
　　时钟抖动导致的 SNR 减弱

　　有几个因素会限制 ADC 的 SNR，例如：量化噪声(管线式转换器中一般不明显)、热噪声(其在低输入频率下限制 SNR)，以及时钟抖动(SNRJitter)(请参见下面方程式 1)。SNRJitter 部分受到输入频率 fIN(取决于 Nyquist 区域)的限制，同时受总时钟抖动量 tJitter 的限制，其计算方法如下：

　　

 

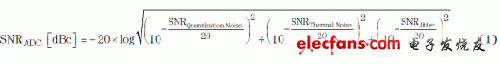
　　SNRJitter[dBc]=-20×log(2π×fIN×tJitter) (2)

　　正如我们预计的那样，利用固定数量的时钟抖动，SNR 随输入频率上升而下降。图 4 描述了这种现象，其显示了 400 fs 固定时钟抖动时一个 14 位管线式转换器的 SNR。如果输入频率增加十倍，例如：从 10MHz 增加到 100MHz，则时钟抖动带来的最大实际 SNR 降低 20dB。

　　

 

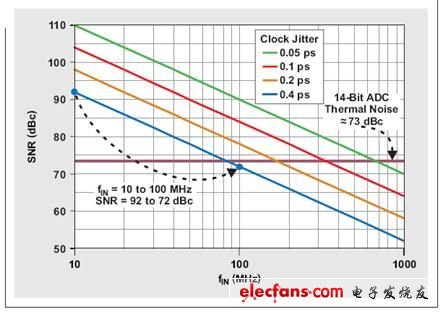
　　如前所述，限制 ADC SNR 的另一个主要因素是 ADC 的热噪声，其不随输入频率变化。一个 14 位管线式转换器一般有 ~70 到 74 dB 的热噪声，如图 4 所示。我们可以在产品说明书中找到 ADC 的热噪声，其相当于最低指定输入频率(本例中为 10MHz)的 SNR，其中时钟抖动还不是一个因素。

　　让我们来对一个具有 400 fs 抖动时钟电路和 ~73 dB 热噪声的 14 位 ADC 进行分析。低输入频率(例如：10MHz 等)下，该 ADC 的 SNR 主要由其热噪声定义。由于输入频率增加，400-fs 时钟抖动越来越占据主导，直到 ~300 MHz 时完全接管。尽管相比 10MHz 的 SNR，100MHz 输入频率下时钟抖动带来的 SNR 每十倍频降低 20dB，但是总 SNR 仅降低 ~3.5 dB(降至 69.5dB)，因为存在 73-dB 热噪声(请参见图 5)：

　　

 

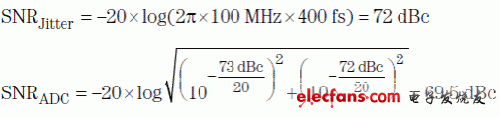
　　现在，很明显，如果 ADC 的热噪声增加，对高输入频率采样时时钟抖动便非常重要。例如，一个 16 位 ADC 具有 ~77 到 80 dB 的热噪声层。根据图 4 所示曲线图，为了最小化 100MHz 输入频率 SNR 的时钟抖动影响，时钟抖动需为大约 150 fs 或更高。

　　确定采样时钟抖动

　　如前所述，采样时钟抖动由时钟的计时不准(相位噪声)和 ADC 的窗口抖动组成。这两个部分结合组成如下：

　　

 

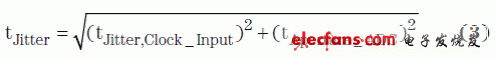
　　我们在产品说明书中可以找到 ADC 的孔径口抖动 (aperture jitter)。这一值一般与时钟振幅或转换速率一起指定，记住这一点很重要。低时钟振幅带来低转换速率，从而增加窗口抖动。

　　时钟输入抖动

　　时钟链(振荡器、时钟缓冲器或 PLL)中器件的输出抖动一般规定在某个频率范围内，该频率通常偏离于基本时钟频率 10 kHz 到 20 MHz(单位也可以是微微秒或者绘制成相位噪声图)，可以将其整合到一起获取抖动信息。但是，低端的 10kHz 和高端的 20MHz 有时并非正确的使用边界，因为它们调试依赖于其他系统参数，我们将在后面进行详细介绍。图 6 描述了设置正确整合限制的重要性，图中的相位噪声图以其每十倍频抖动内容覆盖。我们可以看到，如果将下限设定为 100-Hz 或 10kHz 偏移，则产生的抖动便极为不同。同样地，例如，设置上整合限制为 10 或 20MHz，可得到相比 100MHz 设置极为不同的结果。

　　图 5 产生的 ADC SNR 受热噪声和时钟抖动的限制

　　

 

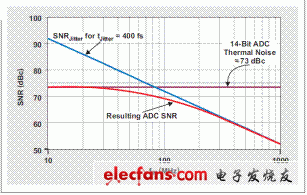
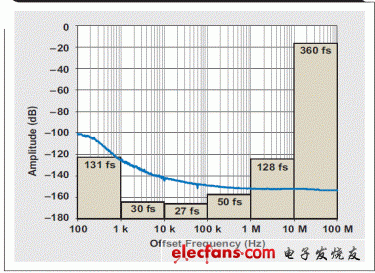
　　图 6 每十倍频计算得到的时钟相位噪声抖动影响

　　

 

　　确定正确的整合下限

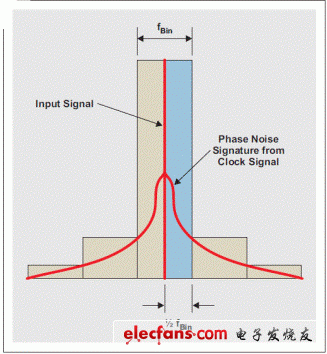
　　在采样过程中，输入信号与采样时钟信号混频在一起，包括其相位噪声。当进行输入信号 FFT 分析时，主 FFT 容器 (bin) 集中于输入信号。采样信号周围的相位噪声(来自时钟或输入信号)决定了邻近主容器的一些容器的振幅，如图 7 所示。因此，小于 1/2 容器尺寸的偏频的所有相位噪声都集中于输入信号容器中，且未增加噪声。因此，相位噪声整合带宽下限应设定为 1/2 FFT 容器尺寸。 FFT 容器尺寸计算方法如下：

　　

 

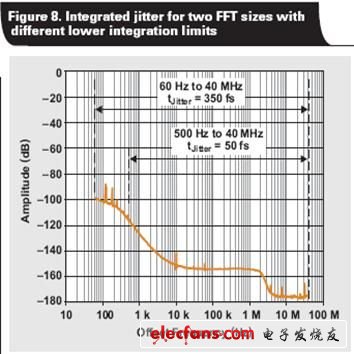
　　为了进一步描述该点，我们利用两个不同的FFT尺寸—131,072 和 1,048,576 点，使用 ADS54RF63 进行实验。采样速率设定为 122.88MSPS，而图 8 则显示了时钟相位噪声。我们将一个 6-MHz、宽带通滤波器添加到时钟输入，以限制影响抖动的宽带噪声数量。选择 1-GHz 输入信号的目的是确保 SNR 减弱仅由于时钟抖动。图 8 表明两个 FFT 尺寸的 1/2 容器尺寸到 40MHz 相位噪声整合抖动结果都极为不同，而“表 1”的 SNR 测量情况也反映这种现象。

　　图 7 近区相位噪声决定主容器附近 FFT 容器的振幅

　　

 

　　设置正确的整合上限

　　图 6 所示相位噪声图抖动贡献量为 ~360 fs，其频率偏移为 10 到 100MHz 之间。这比 100Hz 到 10MHz 之间偏移的所有 ~194 fs 抖动贡献值要大得多。因此，所选整合上限可极大地影响计算得到的时钟抖动，以及预计SNR匹配实际测量的好坏程度。

　　要确定正确的限制，您必须记住采样过程中非常重要的事情是：来自其他尼奎斯特区域的时钟信号伪带内噪声和杂散，正如其出现在输入信号时表现的那样。因此，如果时钟输入的相位噪声不受频带限制，同时没有高频规律性衰减，则整合上限由变压器(如果使用的话)带宽和 ADC 自身的时钟输入设定。一些情况下，时钟输入带宽可以非常大;例如，ADS54RF63 具有 ~2 GHz 的时钟输入带宽，旨在允许高时钟转换速率的高阶谐波。

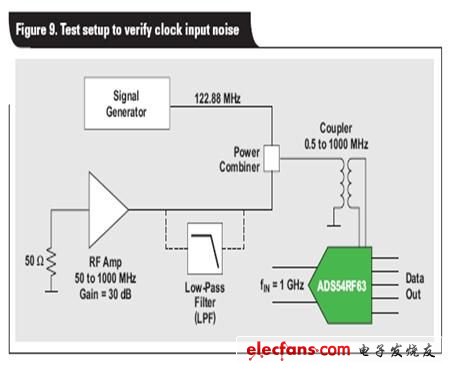
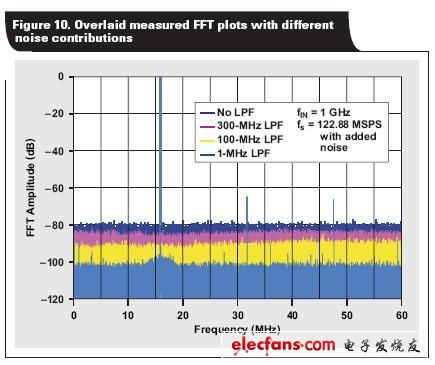
　　若想要验证时钟相位噪声是否需要整合至时钟输入带宽，则需建立另一个实验。ADS54RF63 再次工作在 122.88 MSPS，其输入信号为 1GHz，以确保 SNR 抖动得到控制。我们利用一个 RF 放大器，生成 50MHz 到 1GHz 的宽带白噪声，并将其添加至采样时钟，如图 9 所示。之后，我们使用几个不同低通滤波器 (LPF) 来限制添加至时钟信号的噪声量。

　　ADS54RF63 的时钟输入带宽为 ~2 GHz，但由于 RF 放大器和变压器都具有 ~1 GHz 的 3-dB带宽，因此有效 3-dB 时钟输入带宽被降低至 ~500 MHz。“表 2”所示测得 SNR 结果证实，就本装置而言，实际时钟输入带宽约为 500MHz。图 10 所示 FFT 对比图进一步证实了 RF 放大器的宽带噪声限制了噪声层，并降低了 SNR。

　　该实验表明，时钟相位噪声必需非常低或者带宽有限，较为理想的情况是通过一个很窄的带通滤波器。否则，由系统时钟带宽设定的整合上限会极大降低 ADC 的 SNR。

　　

 

　　

 

　　

 

　　结论

　　本文介绍了如何准确地估算采样时钟抖动，以及如何计算正确的上下整合边界。“第 2 部分”将会介绍如何使用这种估算方法来推导 ADC 的 SNR，以及所得结果与实际测量结果的对比情况。