

数据表示与编码的奥秘:为什么8位数据范围是-128到127?
描述
很表面很浅薄的问题。
简单说爱怎么规定就怎么规定,甚至-1到254都行。无非是显示时通过编码表做个转换的问题而已。
不过,当初选择“补码”这种编码形式,却并不像表面看起来那么浅薄。背后的道道可多着呢。
首先,8位二进制一共可以提供256个“码点”;那么我们就总可以用这些“码点”来编码256种符号。
这种编码方案有很多。最著名的大概就是ASCII码方案了,这个方案规定了英文字符(区分大小写)、0~9这10个数字、标点符号以及一些控制字符如何编码:
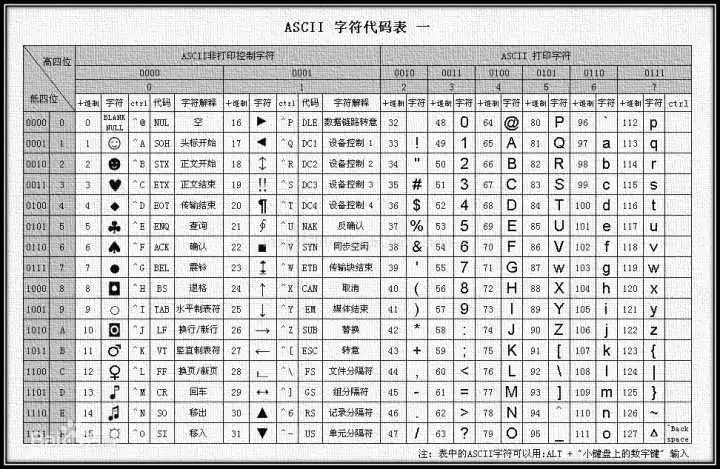
但ASCII码用来编码字符效果不错;拿来存储数字却极为浪费。比如它需要三个字节才能表示123。
为了编码数字,我们需要一个更有效的方案。
一种很自然的想法是,我们就直接把二进制对应的数字值拿来用,这就是最好的编码方案!
于是,8个二进制位就可以表示0~255之间的所有数字——用ASCII码三个字节才能表示的123,直接用二进制编码就是01111011,一个字节足够了。
这个方案只能表示正数;遇到负数怎么办呢?
简单,第一个二进制位拿出来当符号位,剩下七位仍然当数字用,就能表示±127之间的任何数字了。
这个方案就叫“原码”;其中不带符号位的就是无符号数(unsigned)。
原码是一种很初级的编码方案,它仅仅解决了编码问题——从此数字有办法二进制表示了。
但我们在计算机内部表示数字是用来计算的;那么想用原码计算的话,那可就麻烦了……
我们知道,最初CPU的内部最重要的核心器件叫ALU(Arithmetic and Logic Unit算术逻辑单元),其中的A就是数学。
ALU的核心是加法器,这是个随参与计算的数值的二进制位数指数增长的数字电路。较早期的CPU里面绝大多数的逻辑门都被拿来做这个加法器了。
加法器顾名思义只能拿来做加法。
但是没关系,如果你调过机械表,就知道从8点调到1点的方式有两种:一种是往后拨7个小时,一种是往前拨5个小时。
换句话说,在时钟钟面上,8-7和8+(12-7)效果相同,最终得到的都是1.
类似的,1个字节的加减法,如果计算结果超过255就会造成溢出,溢出的高位二进制数据无处存放自动丢弃,计算结果就出错了——但反过来想,这不恰恰就是一个逻辑钟面吗?
显然,我们也可以利用这个性质做减法:减32完全可以当成加(256-32)来算嘛;而由于二进制的特点,256-32恰好又等于32这个数值取反。
类似的,有符号数其实是一个符号位和7个二进制位,7个二进制位能表示的最大数是127;因此减32就可以用加(128-32)代替(和表盘上的12点/0点一样)。
于是,减法器就可以不做,一个加法器就足够用了——省了好大一坨门电路,CPU的制造成本一下子就去了一大块。
既然最终减法一定要这样做……那么从一开始就不应该用原码表示负数,对吧。
不然每次计算都还得用一条指令判断判断符号位,然后该取反取反……这速度可就慢下去了。
如果从一开始,负数就取反表示,那么负数加法完全无需判断,拎起来就加——圆满。
这个编码方案就是所谓的反码。
反码是一个充满了工程师的恶臭味的优秀方案。
说它优秀,是因为它的确解决问题;说它恶臭,是因为它用起来实在麻烦,需要很多“微妙”的调整才能得到正确结果。
比如,它的符号位相加后,如果产生了进位,就要把进位送回去加到最低位上——你得搞一大张真值表才能确定这个做法的正确性。
嗯……这就是最容易产生没人看得懂但绝对不能动不然就会出错的神奇代码的重灾区——反正它就是能工作;刚开始我还知道为什么得这样做,一段时间后就只有上帝知道了。
反码行为奇特的根本原因在于,它有两个零:+0和-0,分别对应于00000000和10000000——还记得吗?我们规定第一位是符号位。因此最前面的0/1是±号,并不是数值。
但+0和-0都是0.它们是同一个数据,却得到了两个码点。
打个比方的话,这就好像夜里12点就是0点一样;结果我们的钟匠师傅没想明白,偏偏要在钟面上、12点和1点之间添加一个零点——然而逻辑上我们仍然需要12小时是一圈。
现在,你还想好好调表吗?算的准准的,8点前拧5个小时就是1点了;结果拧完一看,0点?
彻底乱套了,对吧。
而反码的计算规则呢,无异于规定了过12点的方向——正着过正常去1点,反着过会先停在-0点上,所以必须推一把。
注意这个调整是计算过程的一部分,每次计算都必须即时调整。这是一个额外的负担——和显示时查表转换到光学点阵/向量是不想干的两个过程。
或者说,数据的内部表示和外部显示之间的转换是另外一个必不可少的流程。这里只要不是太过复杂就不能算额外负担;而原码/反码这两个编码方案已经影响了计算过程,造成了额外的性能消耗。
一言以蔽之:能解决问题,但是太难看、太复杂。
一个更好的方案叫补码。
但是在介绍补码之前,我先来讲一个数学概念—群。
群大概来源于“算术运算以及适用算法运算的集合”的抽象,但又超脱于简单的四则运算,是一切计算/变换类似行为的总纲。
在群的观念里,加减乘除都是一种“二元运算”;二元运算是一个集合G中任意两个元素向群中另一个元素的映射。比如1+1就映射到了2。
注意群有“封闭性”,意思是群中任意两个元素经过二元运算后,映射的那个元素都还要在群中。因此(自然数,加减法)就不是一个群,因为减法会映射到负数。
此外,二元运算需要满足结合律,要有单位元(任何元素与之执行二元运算后都会映射到该元素自身),等等。
更复杂的东西我也还看不懂(对不起,俺数学水平太弱鸡了);但了解这么多其实也已经够了:反码存在两个0,意味着对于加法运算来说,它存在两个不同的单位元;而根据群的定义,群里面有且只有一个单位元。
因此,在反码这个基础上无法定义一个群——用人话说就是,你不可能期望找到一种不需要判断的算法,从而基于反码模拟加减法运算。
没错,反码有两个零这事并不像外行想象的那样无关痛痒——它并不仅仅是浪费了一个码点的问题,而是破坏了相关结构的性质的问题。
如何解决这个问题呢?
不妨返璞归真,看看这个问题的本质。
很简单,和上面等待写入时间信息的无字钟面一样:这里有256个不同的二进制编码,我们需要给它们分别指定一个意义。
我们希望它们是连续的编码,且基于二进制的排序不能打乱——这样我们才能使得基于这些码点的、抛弃溢出位的加减法运算构成一个群。
只有它们是一个群,我们才能简单明了的在加法器上支持加减法运算——而不是先算一个瑕疵值然后想办法弥补、把硬件/软件变得复杂。
打个比方的话,就是把这些二进制编码按顺序排于钟面,我们要在上面填上带±号的数字。
原码的问题在于,它的编码排列“不按固定顺序”,使得因此必须把负数先“颠倒”一下(实际上取反)才能用;而反码头疼医头脚疼医脚,大致保证了编码顺序,却没能消除额外的无效码点,造成在±0这个位置两个码点对应一个编码。
这两个编码都没法自然构造出加法群。
借用@任卫同学的这张图:
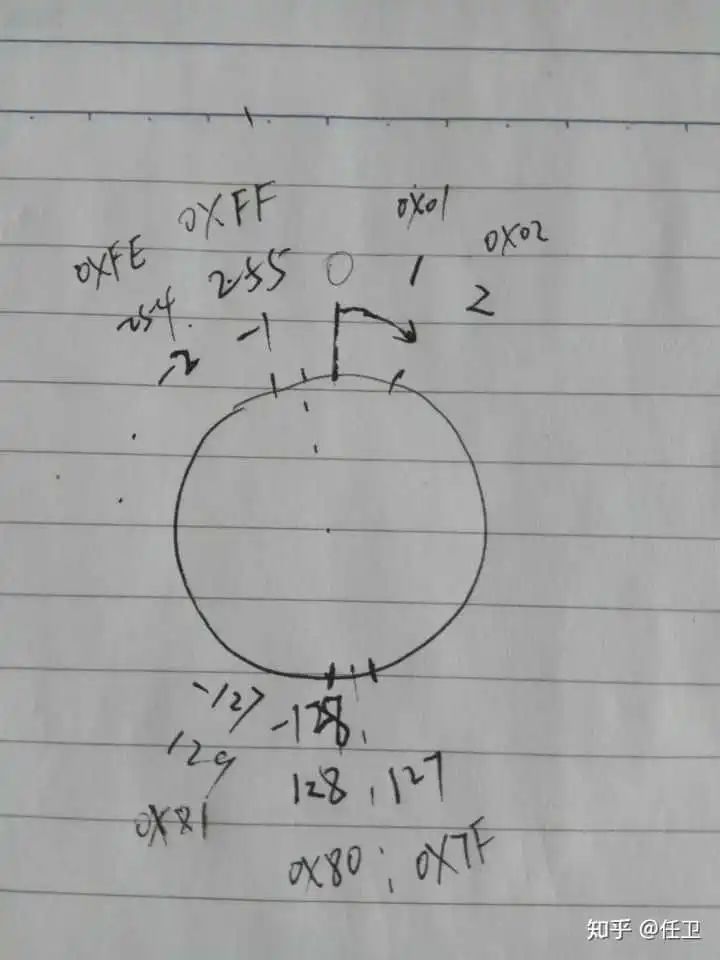
可以很清晰的看出补码编码的连续性。
(相比之下,原码是0 1 2 3……127 -0 -1 -2……-127,顺序上一会儿从小到大一会儿从大到小;补码按照一定的顺序编码但是多了个-0;
只有补码,严格按照统一的顺序连续排列数字)。
既然连续,那么通过加一个值(可能为负)调整对称中心(比如0的位置是00000000还是11111111)、然后再引入模运算剔除高位溢出,这个群就建立起来了。
换句话说,随便你如何编码,只要别改变底层的二进制顺序、不要有跳跃/重复码点,那么这个计算就仍然是一个群。
这个计算过程和最终的显示是完全脱钩的,你不需要在计算时做任何调整——溢出就随它溢出,反正(在模运算的层面上)算出来的值总是对的。这是群的性质所保证的。
(注意是“模运算的层面上”,换句话说算出来的实际意义是什么还是得你自己解释;尤其是产生溢出之后。)
比如,哪怕你把它的编码范围改成[-129, 126]或者[-1, 254],这也仅仅是一个加/减一个整数的映射操作而已;核心计算法则仍然会满足你的需求)。
甚至,你规定0代表1、1代表0,最终也不过是显示时换一个不同的译码表而已,并不改变问题性质。
这个性质是普适的。
7位、8位或者32位、128位二进制全都适用。
一旦明白了这个……再写环形缓冲时,你还要费劲巴拉的检查什么时候需要绕回吗?求个余(或许还需要再视情况不同增减一个常数),完事。
你看,数学这种东西厉害吧?
哪怕群论门槛都摸不到的这么一点点皮毛知识,带来的就是眼界水平的差异。
一旦了解了这点皮毛,关于补码的种种清规戒律神奇规则,也就平常。
但没有这个眼界,就容易像反码那样动辄得咎;反之,随你怎么玩都不会出界。
没错。别看这东西简单;
但想要做第一个提出的人,你还是需要强悍的洞察力的。
站在群论的肩膀上、反向碾压这个问题,这是伽罗瓦之后的现代人特有的福利。
审核编辑:黄飞
-
单片机位数的思考(8位、16位、32位)2025-11-21 68
-
labview数据类型的取值范围是多少2024-09-04 3594
-
TLV571 8位数据采集系统数据表2024-07-29 259
-
603-24-127 数据表2023-05-15 274
-
C语言单片机编程为什么总是用无符号的数据类型来定义2021-07-01 585
-
ADV7195:带三个11位DAC和10位数据输入数据表的多格式逐行扫描/HDTV编码器2021-05-24 729
-
LTC1090:单片机10位数据采集系统数据表2021-05-22 881
-
AD7376:+30 V/±15 V操作128位数字电位器数据表2021-05-16 750
-
AD7314:8引线µSOIC数据表中的低压10位数字温度传感器2021-05-07 667
-
ADV7196A:多格式逐行扫描/HDTV编码器,3个11位DAC,10位数据输入和宏视数据表2021-04-23 572
-
AD1933:带PLL和差分输出的8通道DAC,192 kHz,24位数据表2021-04-15 930
-
请问HT1621驱动芯片内部RAM中的4位数据表示什么?2018-07-04 3482
-
数据表示—常用的信息编码2010-04-15 2405
全部0条评论

快来发表一下你的评论吧 !

