基于互联网的摄像测量系统（一）

D题任务要求

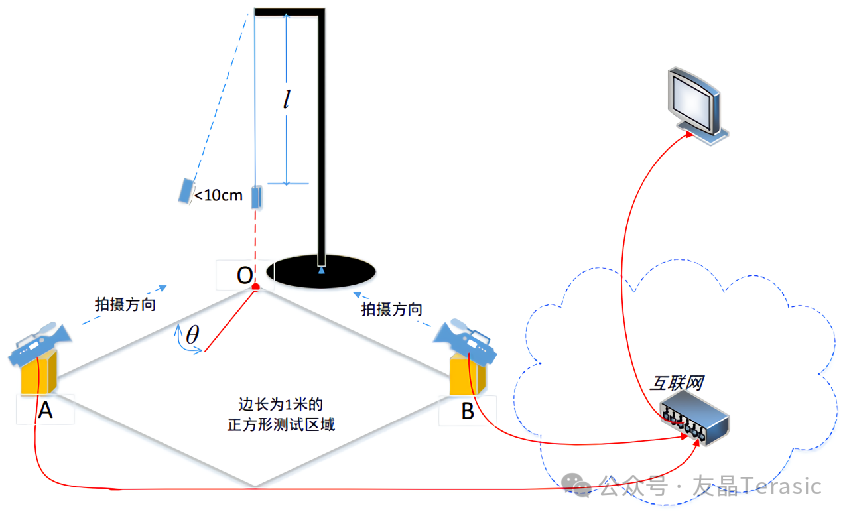
设计并制作一个图中所示的基于互联网的摄像测量系统。图中边长为1米的正方形区域三个顶点分别为A、B和O。系统有两个独立的摄像节点分别放置在A和B，两个摄像节点拍摄尽量沿AO、BO方向正交，并通过一个百兆/千兆以太网交换机与连接在该交换机的一个终端节点实现网络互联。交换机必须为互联网通用交换机，使用的网口可以任意指定。

在O点上方悬挂一个用柔性透明细线吊起的激光笔，透明细线长度为 l，激光笔常亮向下指示，静止下垂时的指示光点与O点重合。

拉动激光笔偏离静止点的距离小于10cm，松开后激光笔自由摆动。应保证激光笔指示光点的轨迹经O点往复直线运动，轨迹与OA边的夹角为 θ。

利用该系统实现对长度 l 和角度 θ 的测量。

基本要求分析

设计并制作两个独立的摄像节点。每个节点由一个摄像头和相应的电路组成，两个摄像节点均可以拍摄到激光笔的运动视频并显示。

设计并制作终端节点。在终端显示器上可以分别和同时显示两个摄像节点拍摄的实时视频。在视频中可以识别出激光笔，并在视频中用红色方框实时框住激光笔轮廓。

测量系统在终端节点设置一键启动。从激光笔摆动开始计时，测量系统通过对激光笔周期摆动视频信号的处理，自动测量长度 l。（50cm ≤ l ≤ 150cm，θ角度自定）  测量完成时，终端声光提示并显示长度 l。要求测量误差绝对值小于 2cm，测量时间小于 30 秒。

题目发挥部分

一键启动后，测量系统通过两个独立摄像节点的网络协同工作。当 θ = 0° 和 θ = 90° 时，能自动测量长度 l（ 50cm ≤ l ≤ 150cm ）。要求测量误差绝对值小于 2cm，测量时间小于 30 秒。

一键启动后，可以测量 θ （ 0° ≤ θ ≤ 90° ） 。要求测量误差绝对值小于 5°，测量时间小于 30 秒。

其他。

硬件方案选择

摄像节点由一个摄像头和相应的电路组成，需要拍摄到激光笔的运动视频并显示。可以使用下面两种方案：

方案一：USB摄像头 + 树莓派

树莓派调用OpenCV库从USB摄像头获取实时图像并显示在HDMI显示器上，然后调用OpenCV库中的图像处理算法识别激光笔，然后在原图像上用红框框住激光笔轮廓，再将激光笔的位置信息和图像通过网络传输到终端节点。

方案二：D8M摄像头 + DE10-Nano开发板

D8M摄像头可通过GPIO接口连接到DE10-Nano开发板上，使用Terasic Camera IP从D8M获取实时视频流数据并显示在HDMI显示器上，再对视频流数据进行处理识别激光笔，然后在原图像上用红框框住激光笔轮廓，再将激光笔的位置信息和图像通过网络传输到终端节点。

方案比较：

方案一采用USB摄像头可以直接使用OpenCV库进行操作，代码简单，但是只能用CPU进行处理，处理效率不够高。

方案二采用GPIO接口的D8M摄像头，直接与DE10-Nano开发板连接，可通过FPGA进行算法加速，CPU只需要读取FPGA端处理好的结果图像再进行简单的计算，可提高处理效率。

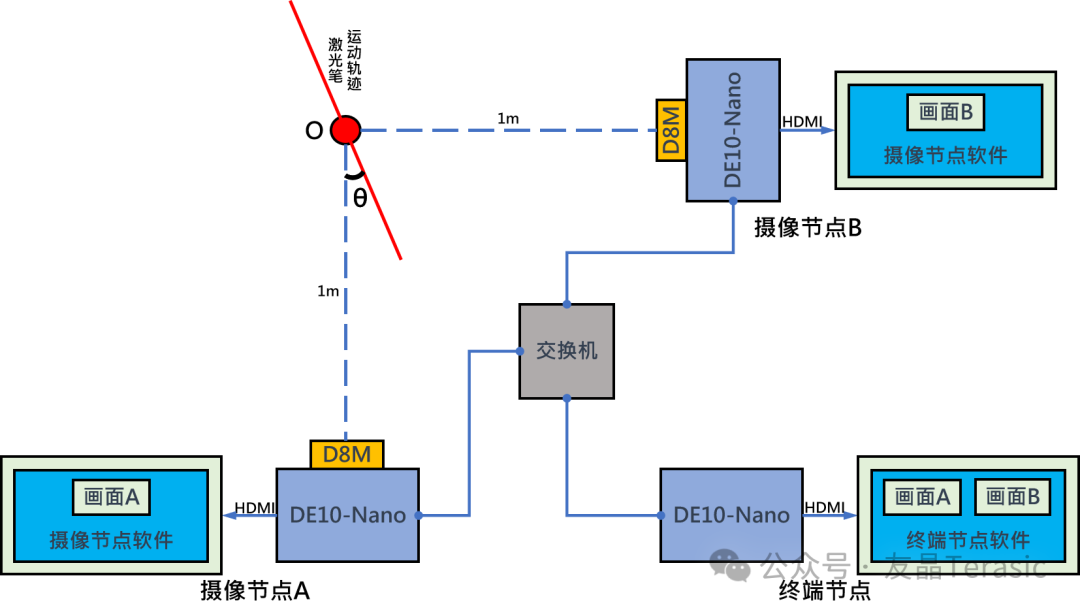
综上所述，为了提高处理效率、缩短测量时间，选择方案二作为摄像节点方案。其系统框图如下：

检测方案选择

运动目标的检测一般有三种方法：背景差分法、帧间差分法和光流法。

背景差分法

背景差分法是采用图像序列中的当前帧和背景参考模型比较来检测运动物体的一种方法，其性能依赖于所使用的背景建模技术，背景图像的建模和模拟的准确程度，直接影响到检测的效果。

帧间差分法

帧间差分法通过对视频或图像序列中相邻两帧做差分运算来获得运动目标的轮廓，可很好地适用于存在多个运动目标和摄像机移动的情况。

当场景中出现物体运动时，帧与帧之间会出现较为明显的差别，两帧相减，得到两帧图像亮度差的绝对值，判断它是否大于阈值来分析视频或图像序列的运动特性，确定图像序列中有无物体运动。

光流法

光流是关于视域中的物体运动检测中的概念，用来描述相对于观察者的运动所造成的观测目标、表面或边缘的运动。光流法的主要任务就是计算光流场，即在适当的平滑性约束条件下，根据图像序列的时空梯度估算

运动场，通过分析运动场的变化对运动目标和场景进行检测与分割。

方案比较：

背景差分法检测运动目标速度快，检测准确，但对于背景的建模和模拟却比较困难，而要提升准确度就会导致算法的计算量增大，实时性不够好；

帧间差分法对包含运动目标的场景有着比较强的鲁棒性，且运算速度快，实时性好，但该方法一般不能完全检测出运动物体的所有像素点，常常在检测到的运动物体内部出现“空洞”现象，因此仅适用于简单的运动物体检测的情况；

光流法不需要预先知道场景的任何信息，就能够检测到运动对象，可处理背景运动的情况，但噪声、多光源、阴影和遮挡等因素会对光流场分布的计算结果造成严重影响，而且光流法计算复杂，也很难实现实时处理。

综上所述，为了能够实时识别到激光笔，且激光笔内部少量像素点的缺失不会影响检测结果，选择帧间差分法作为运动目标检测算法。

长度L的理论计算

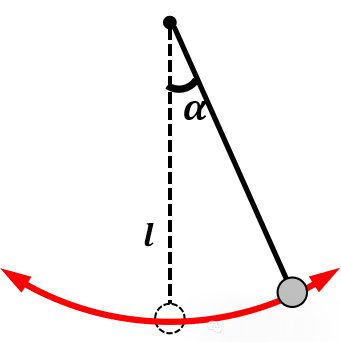
单摆的定义：

将无重细杆或不可伸长的细柔绳一端悬于重力场内一定点，另一端固定一个重小球，就构成单摆。

小角近似简谐运动（一般认为10°以下可以这样近似），单摆能够往复摆动，在非常小的振幅/角度下，单摆做简谐运动，简谐运动方程式如下所示：

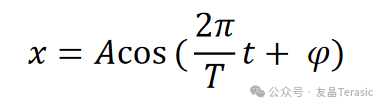
其中，A、 φ 为任意常数，由初值条件给定；而T等于：

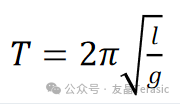
其中 l 为无重细杆或细柔绳的长度， g 为当地的重力加速度。

如果已知简谐运动的周期 T，那么就可以计算得到无重细杆或细柔绳的长度 l：

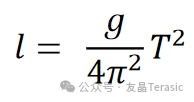
那怎样得到简谐运动的周期T呢？这里采用拟合cos函数。

拟合cos函数

获取数据集

采用拟合cos函数的第一步，就是要获取数据集。

以摄像节点A为例进行介绍，这是摄像节点A拍摄到的画面，将左上角作为坐标原点，通过目标检测算法识别激光笔的位置，然后采集在t时刻对应的激光笔轮廓左上角顶点的坐标值x,y以及长和宽，再计算得到中心点的横坐标xt，将中心点的坐标作为激光笔的坐标。

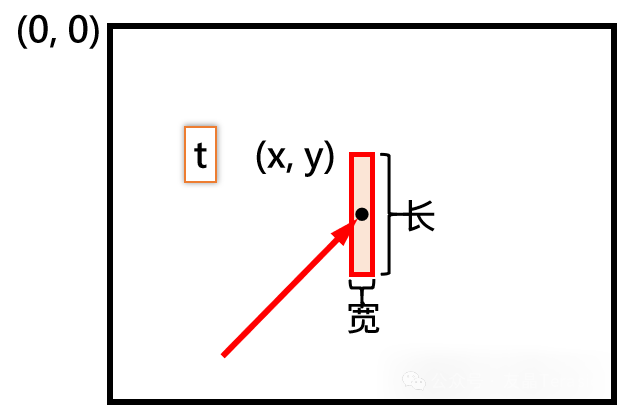
这样就得到了拟合cos函数所需的一组数据，通过测量不同时刻对应的激光笔的位移xt就可以得到一组数据集。

最小二乘法

最小二乘法是解决曲线拟合问题最常用的方法，通过最小化误差的平方和来寻找数据的最佳函数匹配。

余弦曲线表示为：

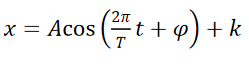
其中包含4个参数，分别是振幅（A）、周期（T）、初相（φ）和偏距（k）。

设(x, y)是一对观测量，且 x和y满足理论函数：y=f(x, ω)，其中ω为待定参数。

为了寻找函数f(x,ω)中参数ω的最优估计值，对于给定m组观测数据(x_i,y_i)(i=1, 2,⋯,m)，求解目标函数

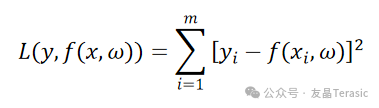
L取最小值时对应的参数ω为最优估计值。

07

角度 θ 的理论计算

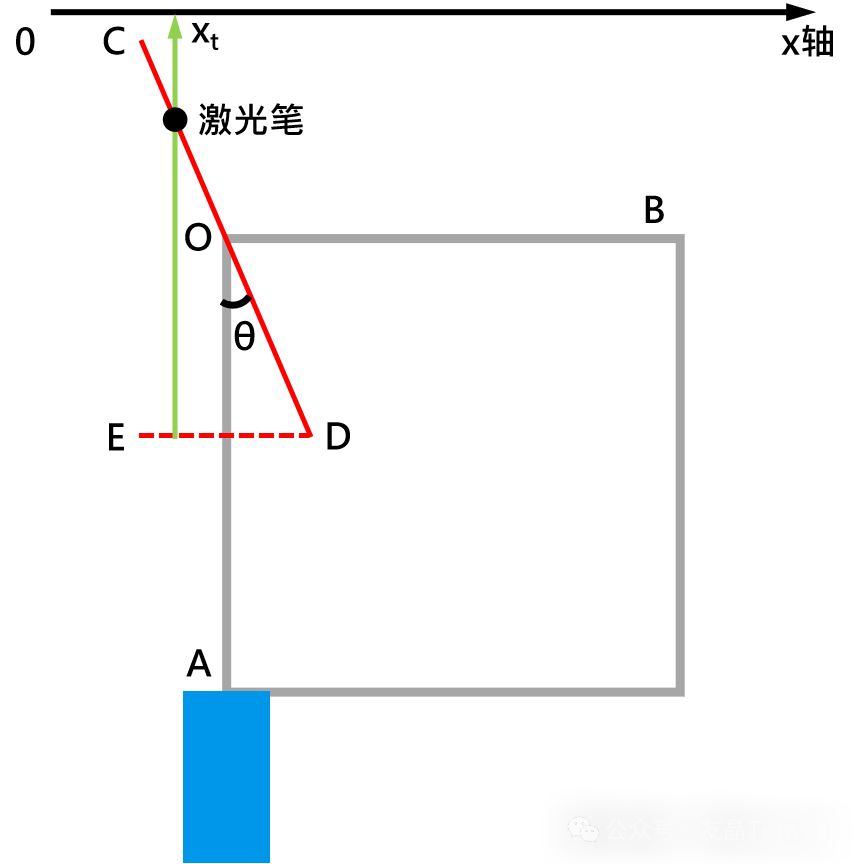
接下来进行角度θ的理论计算，这是测量系统的俯视图：

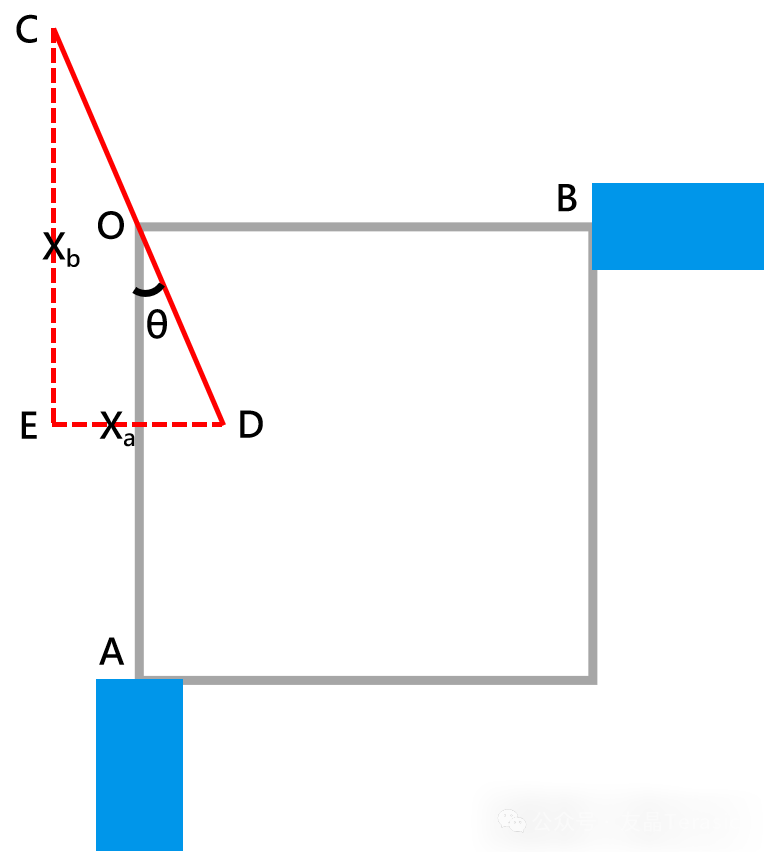
图中红色实线CD是激光笔的运动轨迹，其与OA边的夹角为θ，过点C画OA的平行线，过点D画OB的平行线，交于点E，CE的长度为Xb，DE的长度为Xa。这样就可以得到摄像节点A处拍摄到的激光笔运动轨迹的横向分量DE的运动方程式和分量CE的运动方程式为：

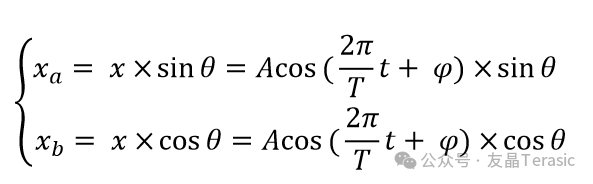
又由于每次拉动激光笔后，角度θ是一个固定值，sinθ和cosθ为常量，所以横向分量和竖直分量也都是简谐运动，而DE的长度为Xa，振幅为Xa/2，所以Xa和Xb可以表示为：

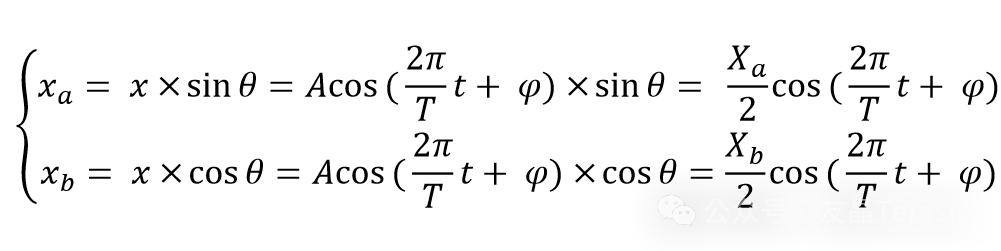
我们将这两个式子相比，可以得到tanθ=Xa/Xb，则由反三角函数的正切公式可以计算得到：

附录

1. D题源码：https://gitee.com/terasic/socfpga-demo/tree/master

2. D题原始文件：

审核编辑：黄飞