简明易懂的机器学习理论基础指南

作者：「报告，今天也有好好学习」

导读

本篇文章，用一种通俗易懂的方式来介绍机器学习的理论基础，是入门机器学习不可错过的文章。

在这里，我要先引用一下一个非常经典的小故事，帮助大家更清楚地理解机器学习。

在一个酒吧里，吧台上摆着十杯几乎一样的红酒，老板跟你打趣说想不想来玩个游戏，赢了免费喝酒，输了付3倍酒钱，那么赢的概率是多少？

你是个爱冒险的人，果断说玩！

老板接着道：你眼前的这十杯红酒，每杯略不相同，前五杯属于「赤霞珠」后五杯属于「黑皮诺」。现在，我重新倒一杯酒，你只需要正确地告诉我它属于哪一类。

听完你有点心虚：根本不懂酒啊，光靠看和尝根本区分辨不出来，不过想起自己是搞机器学习的，不由多了几分底气爽快地答应了老板！

你没有急着品酒而是问了老板每杯酒的一些具体信息：酒精浓度、颜色深度，以及一份纸笔， 老板一边倒一杯新酒，你边疯狂打草稿。

很快，你告诉老板这杯新酒应该是「赤霞珠」。

老板瞪大了眼下巴也差点惊掉，从来没有人一口酒都不尝就能答对，无数人都是反复尝来尝去，最后以犹豫不定猜错而结束。

你神秘地笑了笑，老板信守承诺让你开怀畅饮。微醺之时，老板终于忍不住凑向你打探是怎么做到的。

你炫耀道:无他，但机器学习熟尔。

老板：…

怎么辨别出来的呢？

如下图，故事中的你画了类似这样子的图，就区分出来了

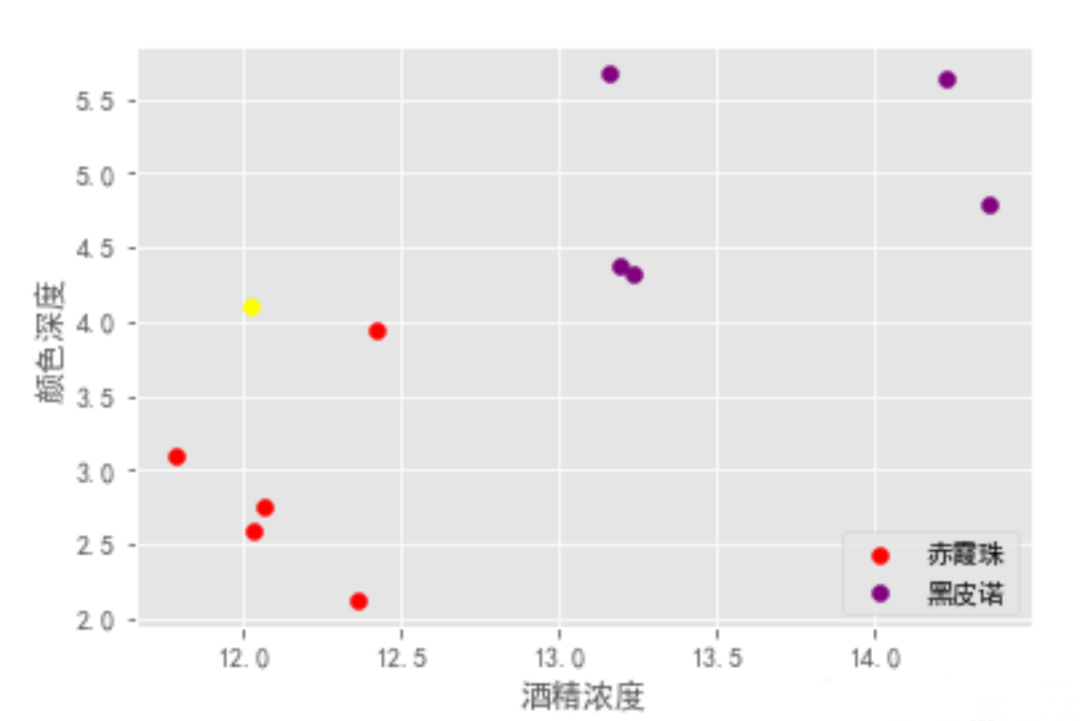
有监督学习

指对数据的若干特征与若干标签(类型)之间的关联性进行建模的过程。只要模型被确定，就可以应用到新的未知数据上。

这类学习过程可以进一步分为「分类」(classification)任务和「回归」(regression)任务。

在分类任务中，标签都是离散值。

而在回归任务中，标签都是连续值。

无监督学习 

指对不带任何标签的数据特征进行建模，通常被看成是一种“让数据自己介绍自己” 的过程。

这类模型包括「聚类」(clustering)任务和「降维」(dimensionality reduction)任务。

聚类算法可以将数据分成不同的组别，而降维算法追求用更简洁的方式表现数据。

半监督学习 

另外，还有一种半监督学习(semi-supervised learning)方法，介于有监督学习和无监督学习之间。通常可以在数据不完整时使用。

强化学习 

强化学习不同于监督学习，它将学习看作是试探评价过程，以"试错" 的方式进行学习，并与环境进行交互已获得奖惩指导行为，以其作为评价。

此时系统靠自身的状态和动作进行学习，从而改进行动方案以适应环境。

（提示：半监督学习和强化学习比较偏向于深度学习）

输入/输出空间、特征空间 

在上面的场景中，每一杯酒称作一个「样本」，十杯酒组成一个样本集。

酒精浓度、颜色深度等信息称作「特征」。这十杯酒分布在一个「多维特征空间」中。

进入当前程序的“学习系统”的所有样本称作「输入」，并组成「输入空间」。

在学习过程中，所产生的随机变量的取值，称作「输出」，并组成「输出空间」。

在有监督学习过程中，当输出变量均为连续变量时，预测问题称为回归问题；当输出变量为有限个离散变量时，预测问题称为分类问题。

过拟合与欠拟合 

先来一句易懂的话：

过拟合简单来说就是模型把训练集的东西学得太精了，对未知的数据效果却很差（打个比方就是考前你练得很不错，给啥做过的题都说得出答案，但是考试的时候碰到新题了就做得很差）

欠拟合就是模型学得很差，打个比方就是考前有题给你练，你也练了，但就是练不会，学不懂。

下面是具体介绍：

当假设空间中含有不同复杂度的模型时，就要面临模型选择(model selection)的问题。

我们希望获得的是在新样本上能表现得很好的学习器。为了达到这个目的，我们应该从训练样本中尽可能学到适用于所有潜在样本的"普遍规律"

我们认为假设空间存在这种"真"模型，那么所选择的模型应该逼近真模型。

拟合度可简单理解为模型对于数据集背后客观规律的掌握程度，模型对于给定数据集如果拟合度较差，则对规律的捕捉不完全，用作分类和预测时可能准确率不高。

换句话说，当模型把训练样本学得太好了的时候，很可能已经把训练样本自身的一些特点当作了所有潜在样本的普遍性质，这时候所选的模型的复杂度往往会比真模型更高，这样就会导致泛化性能下降。这种现象称为过拟合(overfitting)。可以说，模型选择旨在避免过拟合并提高模型的预测能力。

与过拟合相对的是欠拟合(underfitting)，是指模型学习能力低下，导致对训练样本的一般性质尚未学好。

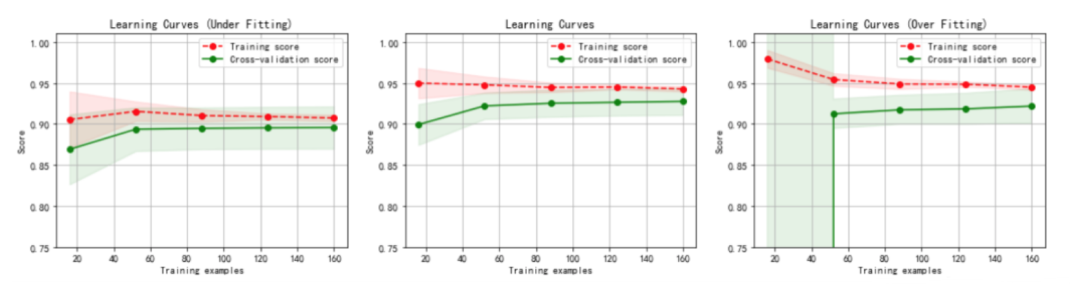
虚线：针对训练数据集计算出来的分数，即针对训练数据集拟合的准确性。

实线：针对交叉验证数据集计算出来的分数，即针对交叉验证数据集预测的准确性。

1.左图：一阶多项式，欠拟合.

训练数据集的准确性（虚线）和交叉验证数据集的准确性（实线）靠得很近，总体水平比较高。

随着训练数据集的增加，交叉验证数据集的准确性(实线)逐渐增大，逐渐和训练数据集的准确性(虚线)靠近，但其总体水平比较低，收敛在 0.88 左右。

训练数据集的准确性也比较低，收敛在 0.90 左右。

当发生高偏差时，增加训练样本数量不会对算法准确性有较大的改善。

2.中图：三阶多项式，较好地拟合了数据集.

训练数据集的准确性（虚线）和交叉验证数据集的准确性（实线）靠得很近，总体水平比较高。

3.右图：十阶多项式，过拟合。

随着训练数据集的增加，交叉验证数据集的准确性(实线)也在增加，逐渐和训练数据集的准确性 (虚线)靠近，但两者之间的间隙比较大。

训练数据集的准确性很高，收敛在 0.95 左右。

交叉验证数据集的准确性值却较低，最终收敛在 0.91 左右。

从图中我们可以看出，对于复杂数据，低阶多项式往往是欠拟合的状态，而高阶多项式则过分捕捉噪声数据的分布规律，而噪声之所以称为噪声，是因为其分布毫无规律可言，或者其分布毫无价值，因此就算高阶多项式在当前训练集上拟合度很高，但其捕捉到的无用规律无法推广到新的数据集上。因此该模型在测试数据集上执行过程将会有很大误差，即模型训练误差很小，但泛化误差很大。

审核编辑：黄飞