一文详解开路PN二极管
描述
什么是开路PN二极管?
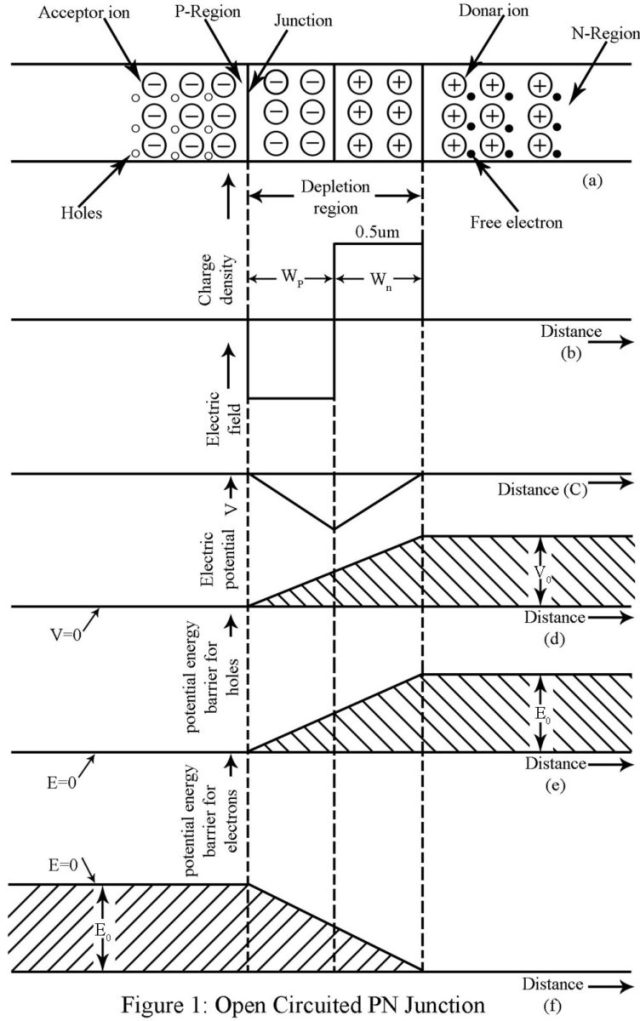
图1(a)显示了受体杂质密度为N的开路pn二极管一个在p区和供体杂质密度N中D在 n 区域中。我们假设每个受体原子都电离,产生一个不动的带负电荷的受体离子和一个移动的空穴。类似地,每个供体原子都电离,产生一个不动的带正电的供体离子和一个移动电子。在图1(a)中,不动的受体离子用圆圈内的减号表示,而不动的供体离子用圆圈内的加号表示。我们假设一开始在p区(在结的左侧)中只有空穴,在n区(在结的右手边)只有电子。
空间电荷区域或耗尽区域 |开路PN二极管
一开始,从左到右存在穿过结点的空穴密度梯度和从右到左的自由电子密度梯度。因此,空穴从p区扩散到n区,而自由电子从n区扩散到p区。进入 n 区时的空穴与结附近的电子结合。因此,这些最初覆盖或中和结附近正供体离子的电子通过与入射空穴的结合而丢失。这个过程使正离子未归化或未被覆盖。类似地,负电子在通过结扩散到p区时与结附近的空穴结合。因此,这些最初中和或覆盖负离子的空穴因复合而丢失。这个过程使负离子未归化或未被发现。图1(b)给出了电荷密度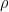 与距离的关系图的典型形状。该曲线的确切形状取决于二极管结,无论是均匀级配还是阶梯级级或阶梯级或任何其他类型。
与距离的关系图的典型形状。该曲线的确切形状取决于二极管结,无论是均匀级配还是阶梯级级或阶梯级或任何其他类型。
结区域的移动电荷载流子已经耗尽。因此,该区域被称为枯竭区域。它也被称为空间电荷区或过渡区。耗尽区非常薄,通常为 0.5 微米 (0.5×10^-6^m) 厚。在耗尽区的左侧,移动载流子密度为 ,而在右侧,载流子密度为 。
电场强度 |开路PN二极管
从图1(b)中我们发现,结处的空间电荷密度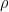 为零,右边为正,左边为负。这样的电荷分布形成电线杆,并产生从右到左的通量线。相应的电场强度为负,并随过渡区域的距离而变化,如图1(c)所示。这种电场倾向于从右向左发送漂移电流,与扩散电流相反。因此,随着载流子在结上的扩散,移动载流子的耗尽,电场逐渐积累,直到达到平衡,当电场完全不允许电荷载流子的扩散过程时。在稳态下,空穴(电子)扩散电流产生净零空穴(电子)电流,这是开路器件的基本条件。
为零,右边为正,左边为负。这样的电荷分布形成电线杆,并产生从右到左的通量线。相应的电场强度为负,并随过渡区域的距离而变化,如图1(c)所示。这种电场倾向于从右向左发送漂移电流,与扩散电流相反。因此,随着载流子在结上的扩散,移动载流子的耗尽,电场逐渐积累,直到达到平衡,当电场完全不允许电荷载流子的扩散过程时。在稳态下,空穴(电子)扩散电流产生净零空穴(电子)电流,这是开路器件的基本条件。
泊松方程状态, 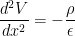 (1)
(1)
电介电常数在哪里 ?
?
然后电场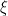 由下式给出,
由下式给出,
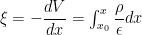 .......(2)
.......(2)
其中 X = X 0 ,其中 X0表示耗尽区域的左边缘。
电位 V |开路PN二极管
静电势 V 由下式给出,
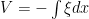 (3)
(3)
因此,静电势V是图1(c)中电场积分的负数。图1(d)绘制了耗尽区静电势V与距离x的关系图,以p区的电位为参考电位或零电位。然后,n 区的电位高出 V0如图1(d)所示。电位差 V0横跨结点的只是接触电位 V0正如给出的
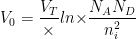 .......(4)
.......(4)
V 的值0Ge 为 0.2 至 0.4 伏,Si 为 0.5 至 0.9 伏。这 V0远大于 T=300 K 时电荷载流子的平均热能 0.02eV。
势能势垒 |开路PN二极管
势能 E 等于势 V 和载流子电荷的乘积。因此,图1(e)绘制了势能势垒,以防止空穴从p区进一步扩散到n区,在p区中E = 0。以焦耳为单位的势垒高度等于 E 0 = qV(质量源)0以伏特为单位。类似地,防止电子从 n 区流向 p 区的势能势垒等于 -qV0并绘制在图1(f)中,在p区域中取E = 0。
示例 1:
- Ge pn 二极管的 p 区和 n 区电阻率分别为 5 欧姆厘米和 3 欧姆厘米。计算势能势垒的高度。
- 如果 p 和 n 个区域的掺杂密度各增加一倍,则重复部分“a”。鉴于:Q 1.6 X 10^-19^哥伦布; 厘米 ^2^ /V-s,厘米 ^2^ /V-s,300 K 时温度的当量为 0.026 伏,n
我= 2.5×10 ^13^ /厘米 ^3^ .
溶液:
对于(a)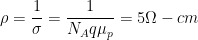
因此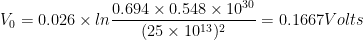
因此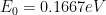
对于(b)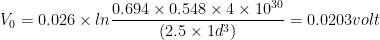
因此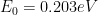
-
二极管全面详解2013-03-31 16753
-
一文读懂稳压二极管2021-11-12 1440
-
变容二极管,变容二极管是什么意思2010-02-27 1900
-
稳压二极管(齐纳二极管),稳压二极管是什么意思2010-03-01 5234
-
变容二极管,变容二极管电路,变容二极管原理2010-03-05 3602
-
贴片二极管正负极如何区分_贴片二极管封装详解_贴片二极管封装图2017-12-12 198393
-
肖特基二极管应用_肖特基二极管应用电路_肖特基二极管在数字电路中的应用详解2018-01-21 20492
-
一文详解射频电路的PIN二极管2021-03-20 17867
-
一文详解肖特基二极管和PN结二极管的选型2021-05-08 8086
-
二极管钳位电路的作用2022-12-08 4640
-
肖特基二极管的原理详解2023-01-31 4982
-
一文详解半导体二极管2023-03-21 3135
-
二极管工作电压 二极管电流详解2023-08-28 12007
-
一文详解TVS二极管2023-11-29 2997
-
肖特基二极管是稳压二极管吗2024-01-11 3433
全部0条评论

快来发表一下你的评论吧 !