

高速模数转换器输入阻抗测量方法
设计测试
描述
本文解释了为什么ADC输入阻抗随频率而变化,以及为什么这是个电路设计难题;然后比较了确定输入阻抗的两种方法:利用网络分析仪测量法和利用数学分析方法计算法。本文还介绍了正确使用网络分析仪的过程,并且提供了一个数学模型,其计算结果与实际测量结果非常接近。
“有缓冲”或“无缓冲”
考虑输入阻抗的影响时,设计人员一般可以在两类高速ADC之间选择:有缓冲和无缓冲(即采用开关电容)。虽然有许多不同的转换器拓扑结构可供选择,但本文讨论的应用仅涉及流水线架构。
常用的CMOS开关电容ADC无内部输入缓冲器。因此,其功耗远低于缓冲型ADC。外部前端直接连接到ADC的内部开关电容采样保持(SHA)电路,这带来两个问题。
第一,当ADC在采样与保持两种模式之间切换时,其输入阻抗会随频率和模式而变化。第二,来自内部采样电容和网络的电荷注入会将少量信号(与高频成分混合,如图1所示)反射回前端电路和输入信号,这可能导致与转换器模拟输入端相连的元件(有源或无源)发生建立(settling)错误。
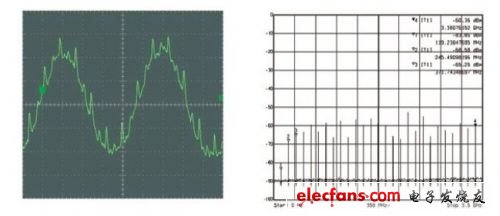
图1:此图反映了内部采样电容的时域电荷注入(单端)与频域电荷注入的对比关系。
通常,当频率较低时(《100MHz),这类转换器的输入阻抗非常高(数千Ω左右);当频率高于200MHz时,差分输入阻抗跌落至大约200Ω。输入阻抗的虚部(即容性部分)也是如此,低频时的容抗相当高,高频时逐渐变小到大约1-2pF。“匹配”这种输入结构是个极具挑战性的设计问题,特别是当频率高于100MHz时。
输入端采用差分结构很重要,尤其是对于频域设计。差分前端设计能够更好地对电荷注入进行共模抑制,并且有助于设计。
采用带输入缓冲的转换器更便于设计。但不利的一面是这类转换器的功耗更高,因为缓冲器必须设计得具有高线性和低噪声特性。输入阻抗通常规定为固定的差分R||C阻抗。它由一个晶体管级进行缓冲,该级以低阻抗驱动转换过程,因此显著减小了电荷注入尖峰和开关瞬变。
与开关电容型ADC不同,输入终端在转换过程的采样和保持阶段几乎无变化。因此,相比于无缓冲型ADC,其驱动电路的设计容易得多。图2为缓冲型和无缓冲型ADC的内部采样保持电路的结构简图。
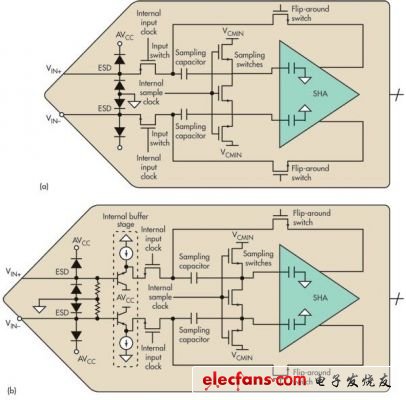
图2: 所示是无缓冲(a)和有缓冲(b)高速流水线ADC采样和保持电路的比较。
转换器的选择可能很难,但如今的大部分设计都力求更低功耗,因此设计人员往往采用无缓冲型转换器。如果线性指标比功耗更重要,则通常选用缓冲型转换器。应当注意,无论选择何种转换器,应用的频率越高,则前端设计就越困难。单靠选择缓冲型转换器并不能解决所有问题。不过在某些情况下,它可能会降低设计复杂性。
转换器输入阻抗计算:测量方法
表面上,这似乎非常棘手,但其实有多种方法可以测量转换器的阻抗。技巧在于利用网络分析仪来完成大部分琐碎工作,不过这种设备可能价格不菲。其优点是,当今的网络分析仪能够实现许多功能,像迹线计算和去嵌入等;对于阻抗转换等任务,它可以直接给出答案,而不需要使用外部软件。
测量转换器的阻抗需要两块电路板、一台网络分析仪和一点“入侵”知识。第一块板焊接有ADC/DUT(待测器件),还焊接了其它元件以提供偏置和时钟(图3a)。第二块高速ADC评估板去除了前端电路,仅留连至转换器模拟输入引脚的走线(图3b)。

图3: ADC的阻抗测量需要一块ADC评估板(a)且要将(a)中的前端去掉以用于测量(b)。
第二块板除去了拆掉的前端电路的任何走线寄生效应。为此,必须使用与图3b所示一模一样但没焊装器件的电路裸板(图4a)。然后切割该裸板,只剩下前端电路走线进入ADC的模拟输入引脚的那部分(图4b)。
图4: 为去掉被剥离的前端电路的导线寄生效应,应使用图3b所示的未焊件裸板(a)。该板的一个剪切版只允许前端电路导线连接到ADC的模拟输入引脚(b)。
需要在转换器的引脚处安装一个连接器(通常会有足够的铜来完成这一任务)。在此阶段可发挥创造性以保证该连接器的牢固连接。通常,ADC的裸露焊盘(epad)可用于实现转换器本身到地的连接。假设前端电路的两条差分走线相等且对称,那么只需要使用其中的一条走线。该板用于实现“通过”测量,最后将从焊有器件电路板的测量结果中减去前一测量结果。
下一步是对剪切后的小裸板(图4b所示的第二块板)实施“通过”测量,以测量S21(图5)。这个文件(应以touchstone格式或?.S2P文件形式保存)将成为去嵌入文件,用以从焊有器件的板中剔除所有走线寄生效应。
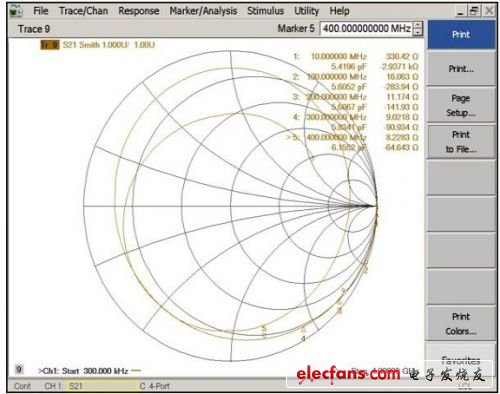
图5: 图4b所示剪切板的去掉前端电路后的导线阻抗。
然后只需以差分配置将焊件板(图3b所示的第一块板)连接到网络分析仪。应为该板提供电源和时钟,以确保能捕捉到测量过程中转换器内部前端设计的任何寄生变化。
焊件板“上电”后,转换器看起来像是在典型应用中。在此测量中,将先前在切割裸板的各端口(各模拟输入走线)上测得的板寄生效应(图6)去掉。最终将从当前ADC测量结果中减去板寄生效应,仅在图中显示封装和内部前端阻抗(图7)。
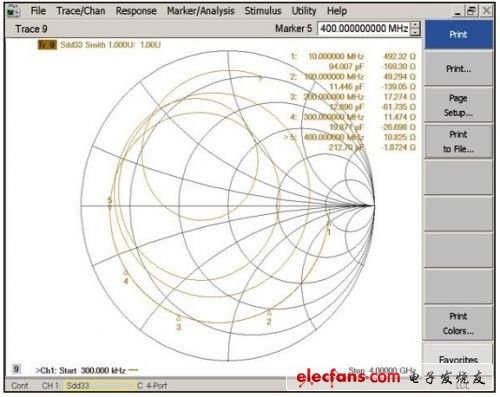
图6: 这条曲线说明了没去掉前端电路寄生效应的ADC阻抗。
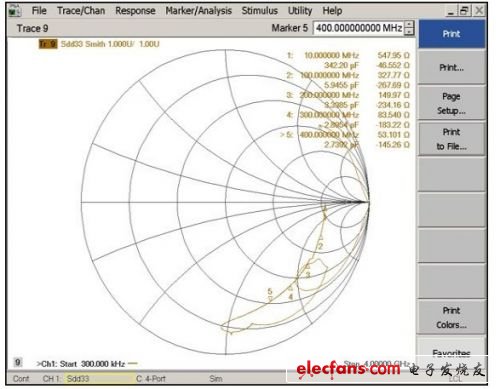
图7: 这条曲线说明了去掉前端电路寄生效应的ADC的阻抗。
转换器输入阻抗计算:数学方法
现在我们通过数学方法分析一下,看花在实验室测量上的时间是否值得。可对任何转换器的内部输入阻抗实施建模(图8)。该网络是表述跟踪模式下(即采样时)输入网络交流性能的一个良好模型。
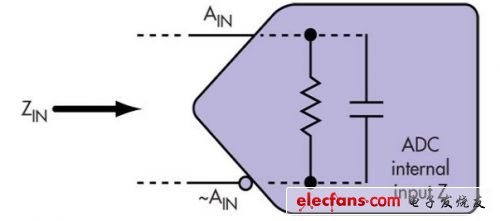
图8: 跟踪模式(实施采样时)下,ADC内部输入网络的AC性能。
ADC internal input Z:ADC内部输入阻抗
通常,任何数据手册都会给出某种形式的静态差分输入阻抗、以及通过仿真获得的R||C值。本文所述方式所用的模型非常简单,目的是求出高度近似值并简化数学计算。否则,如果等效阻抗模型还包括采样时钟速率和占空比,那么很小的阻抗变化就可能使数学计算变得异常困难。
还应注意,这些值是ADC内部电路在跟踪模式下采样过程(即对信号进行实际采样)中的反映。在保持模式下,采样开关断开,输入前端电路与内部采样处理或缓冲器隔离。
推导该简单模型(图8)并求解实部和虚部:
Z0 = R, Z1 = 1/s • C, s = j • 2 • π • f, f = frequency
ZTOTAL = 1/(1/Z0 + 1/Z1) = 1/(1/R + s • C) = 1/((1 + s • R • C)/R)) = R/(1 + s • R • C)
代换s并乘以共轭复数:
ZTOTAL = R/(1 + j • 2 • π • f • R • C) = R/(1 + j • 2 • π • f • R • C) • ((1 – j • 2 • π • f • R • C)/(1 – j • 2 • π • f • R • C)) = (R –j • 2 • π • f • R2 • C)/(1 + (2 • π • f • R • C)2)
求出“实部”(Real)和“虚部”(Imag):
ZTOTAL = Real + j • Imag = R/(1 + (2 • π • f • R • C)2) + j • (–2 • π • f • R2 • C)/(1 + 2 • π • f • R • C)2)
Real = R/(1 + (2 • π • f • R • C)2) Imag = (–2 • π • f • R2 • C)/(1 + (2 • π • f • R • C)2)
这一数学模型与跟踪模式下的交流仿真非常吻合(图9和图10)。这个简单模型的主要误差源是阻抗在高频时的建立水平。注意,这些值一般是通过一系列仿真得出的,相当准确。
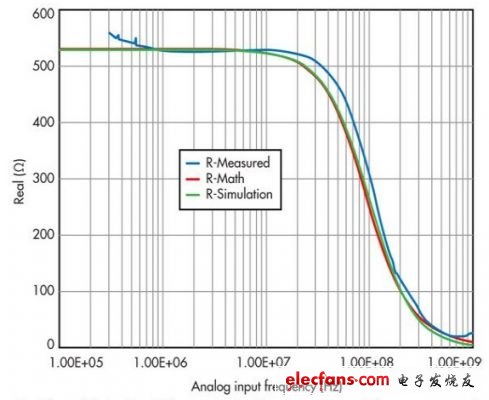
图9: 显示的是转换器输入阻抗曲线的“实部”部分,它比较了经测量、数学和仿真方法得到的结果。
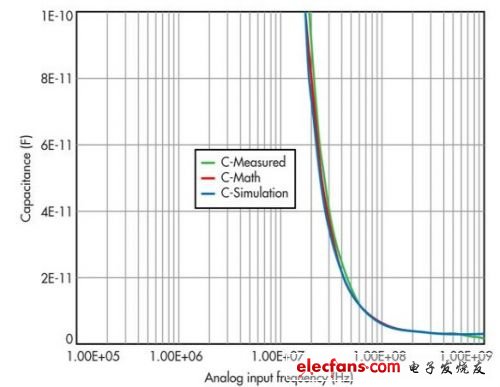
图10: 显示的是转换器输入阻抗曲线的“虚部”部分,它比较了经测量、数学和仿真方法得到的结果。
现在讨论图9和图10所示的测量结果。所有三条曲线并不完全重合,但很接近,这是因为某些测量误差总是存在的,而且仿真可能并未考虑到转换器的所有封装寄生效应。因此,一定程度的不一致是正常的。尽管如此,这些曲线在形状和轮廓方面都很相似,相当近似地给出了转换器的阻抗特性。
注意,网络分析仪只能在其特征阻抗标准乘/除10倍的范围内提供可信的测量结果。如果网络分析仪的特征阻抗为50Ω,那么只能在5Ω到500Ω的范围内实现令人满意的测量。这也是数据手册中更愿意列出简单R||C值的原因之一。
ADC输入阻抗总结
了解转换器阻抗是信号链设计的一个重要内容。总之,若非真正需要,为什么要浪费大笔资金去购买昂贵的测试设备,或者费力去测量阻抗?不如使用数据手册提供的RC并联组合阻抗并稍加简单计算,这种获取转换器阻抗曲线的方法更快捷、更轻松。
-
一种实现高速模数转换器输入阻抗测量的方法2023-11-13 1496
-
输入阻抗的测量方法2023-09-26 8949
-
高速模数转换器的INL/DNL测量2023-02-24 9836
-
模数转换器是输入还是输出_模数转换器误差2023-02-14 2661
-
高速率的逐次逼近模数转换器ADS8412是如何设计的?2021-04-14 2166
-
具有轨至轨输出级的LTC6241模数转换器的性能及应用分析2020-08-31 1516
-
基于模数转换器LTC6241的轨对轨精确测量系统的实现2020-08-15 1186
-
高速模数转换器输入阻抗测量的两种方法2019-06-05 2760
-
使用高速数据转换器的LIDAR脉冲飞行时间测量方法2018-10-09 3275
-
如何快速测量ADC输入阻抗和印刷电路板(PCB)寄生的步骤详细概述2018-05-18 2194
-
NXP 高速模数转换器2012-08-14 2668
-
基于网络分析仪测量高速模数转换器输入阻抗详解2012-05-24 2755
-
数模和模数转换器2009-09-16 7664
-
高速模数转换器(ADC)的INL/DNL测量2009-08-21 2319
全部0条评论

快来发表一下你的评论吧 !

