机器学习六大核心算法深度解析

大家好，我是花哥。

近期，吴恩达老师 在其创办的人工智能周讯《The Batch》上更新了一篇博文，总结了机器学习领域多个基础算法的历史溯源，并总结到：（机器学习中）不断学习与更新基础知识是十分重要的。与其他技术领域一样，随着研究人员的增加、研究成果数量的增长，机器学习领域也在不断发展，但有些基础算法与核心思想的贡献是经得起时间考验的。

这六种算法分别是：线性回归、逻辑回归、梯度下降、神经网络、决策树与k均值聚类算法。

本文会深入介绍下这六种基础算法的背景、原理、优缺点、应用场景。

1、线性回归

 

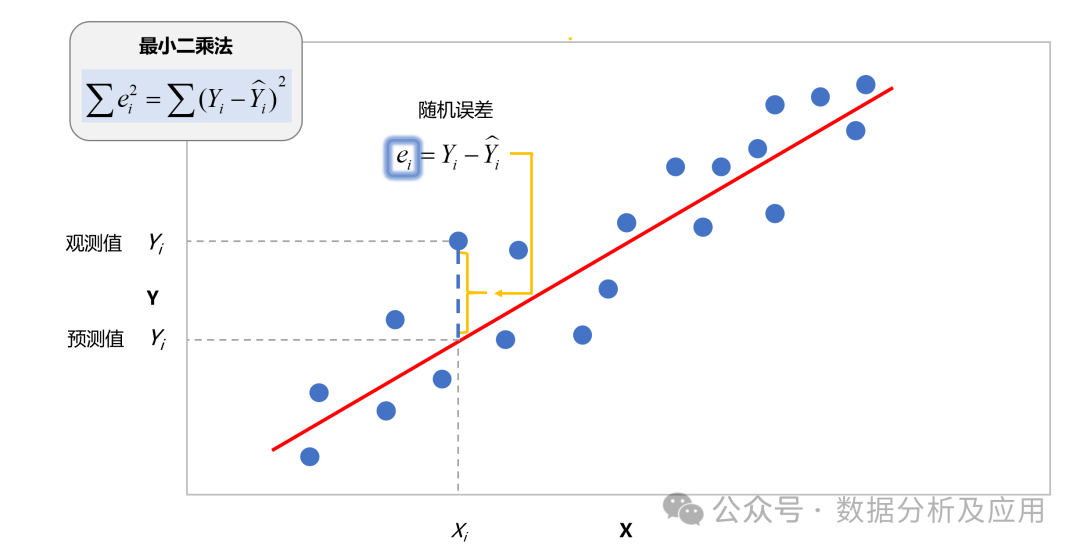
算法历程：线性回归是一种古老的统计方法，它试图找到最佳拟合数据的直线或超平面，最早可以追溯到19世纪初的高斯最小二乘法理论。

原理：线性回归通过最小化预测值与真实值之间的平方误差来找到最佳拟合的线性方程。

训练过程：

选择一个线性方程的形式（例如：y = mx + b）。

通过最小化平方误差来找到最佳参数（m 和 b）。

使用梯度下降或最小二乘法算法来学习参数。

优点：

简单易懂，计算效率高。

适用于线性关系的数据。

缺点：

对非线性关系的数据效果不佳。

对异常值敏感。

适用场景：房价预测、股票预测、销售预测等线性关系明显的场景。

Python示例代码：

 

 

from sklearn.linear_model import LinearRegression
import numpy as np

# 假设X是特征数据，y是目标变量
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([2, 4, 6, 8, 10])

# 创建并训练模型
model = LinearRegression()
model.fit(X, y)

# 预测
prediction = model.predict([[6]])
print(prediction)

二、逻辑回归

 

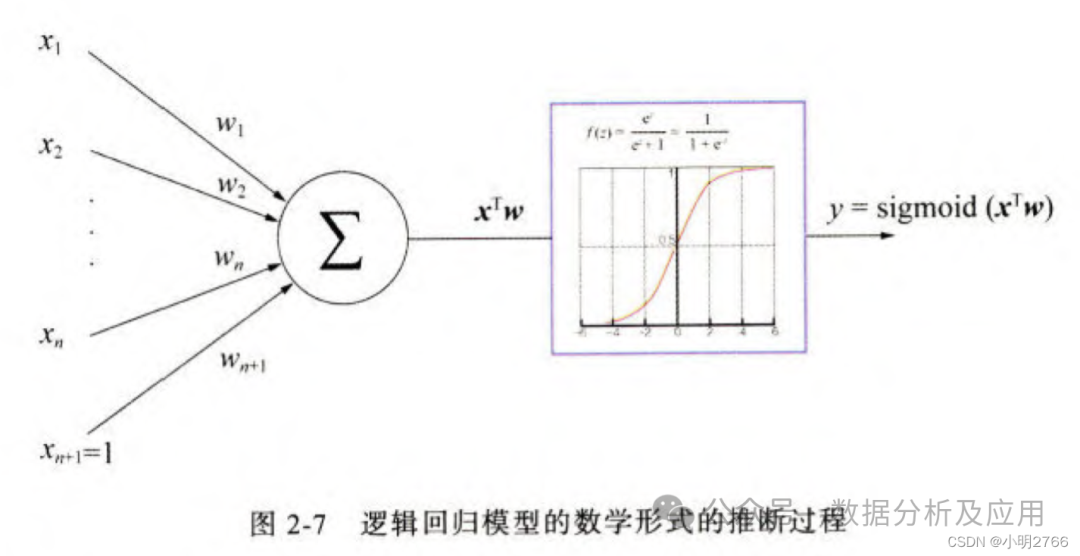
算法历程：逻辑回归最初是由David Cox在1958年提出，但真正被广泛应用是在统计和机器学习领域对二分类问题的研究中。

原理：逻辑回归是一种广义线性模型，通过逻辑函数（通常是sigmoid函数）将线性回归的输出映射到[0, 1]区间，从而得到属于某个类别的概率。

训练过程：

选择sigmoid函数作为激活函数。

通过最大化对数似然函数或使用梯度下降来找到最佳参数。

优点：

计算效率高，实现简单。

可以输出概率，便于解释。

缺点：

对非线性可分的数据效果可能不佳。

对特征间的多重共线性敏感。

适用场景：二分类问题，如垃圾邮件分类、疾病检测等。

Python示例代码：

from sklearn.linear_model import LogisticRegression
import numpy as np

# 假设X是特征数据，y是二分类标签
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([0, 0, 1, 1])

# 创建并训练模型
model = LogisticRegression()
model.fit(X, y)

# 预测概率
probs = model.predict_proba([[9, 10]])
print(probs)

 

 

三、梯度下降

 

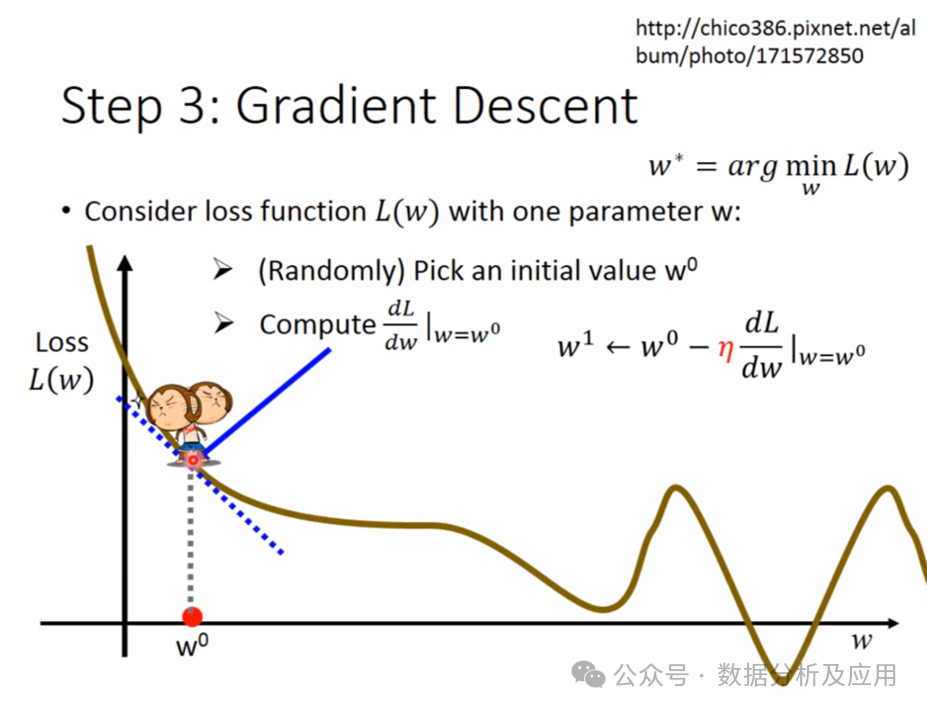
算法历程：梯度下降是一种优化算法，最早由Cauchy在1847年提出，用于求解函数的局部最小值。梯度下降对复杂的神经网络提供了一种有效的优化方法，大大推进了深度学习的发展。

原理：通过计算损失函数关于模型参数的梯度，并沿梯度的反方向更新参数，以逐渐减小损失函数的值。

训练过程：

初始化模型参数。

计算损失函数关于参数的梯度。

使用学习率乘以梯度来更新参数。

重复步骤2和3，直到满足停止条件（如达到最大迭代次数或梯度足够小）。

优点：

通用性强，可用于多种机器学习模型。

简单直观，易于实现。

缺点：

对学习率的设置敏感。

可能陷入局部最小值。

适用场景：用于训练各种机器学习模型，如线性回归、逻辑回归、神经网络等。

Python示例代码（以线性回归为例）：

import numpy as np

# 假设X是特征数据，y是目标变量
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([2, 4, 6, 8, 10])

# 初始化参数
m, b = 0, 0
learning_rate = 0.01
epochs = 1000

# 梯度下降训练过程
for epoch in range(epochs):
    y_pred = m * X + b
    loss = np.mean((y_pred - y) ** 2)
    grad_m = 2 * np.mean((y_pred - y) * X)
    grad_b = 2
    *grad_b = 2 * np.mean(y_pred - y)
    
    # 更新参数
    m -= learning_rate * grad_m
    b -= learning_rate * grad_b
    
    # 可选：打印损失值以观察收敛情况
    if epoch % 100 == 0:
        print(f'Epoch {epoch}, Loss: {loss}')

# 打印最终参数和损失
print(f'Final m: {m}, Final b: {b}, Final Loss: {loss}')

 

 

四、神经网络

 

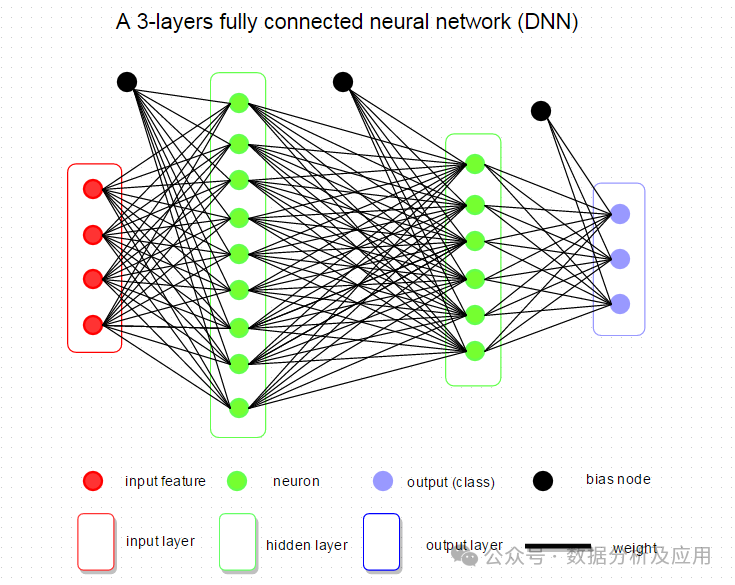
算法历程：神经网络的研究始于20世纪40年代，由于早期算力的瓶颈，经历了多次兴衰。直到2006年深度学习的提出，数据、算力、算法的发展，神经网络再次成为研究热点。

原理：神经网络通过模拟人脑神经元的连接和工作方式，构建多层的神经元网络来学习和逼近复杂的函数。

训练过程：

前向传播：输入数据通过神经网络得到输出。

计算损失：比较输出与真实值之间的差距。

反向传播：根据损失函数计算梯度，并通过链式法则逐层回传梯度。

更新参数：使用梯度下降或其他优化算法更新神经网络的权重和偏置。

优点：

强大的表示学习能力，适用于复杂的问题。

可以自动提取特征。

缺点：

容易过拟合，需要正则化技术。

训练需要大量数据和时间。

适用场景：图像识别、语音识别、自然语言处理等复杂任务。

Python示例代码（使用Keras库构建简单神经网络）：

 

 

from keras.models import Sequential
from keras.layers import Dense
import numpy as np

# 假设X是特征数据，y是目标变量
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 0])

# 创建神经网络模型
model = Sequential()
model.add(Dense(2, input_dim=2, activation='relu'))  # 隐藏层
model.add(Dense(1, activation='sigmoid'))  # 输出层

# 编译模型
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

# 训练模型
model.fit(X, y, epochs=100, batch_size=1)

# 预测
predictions = model.predict(X)
print(predictions)

 

 

五、决策树

 

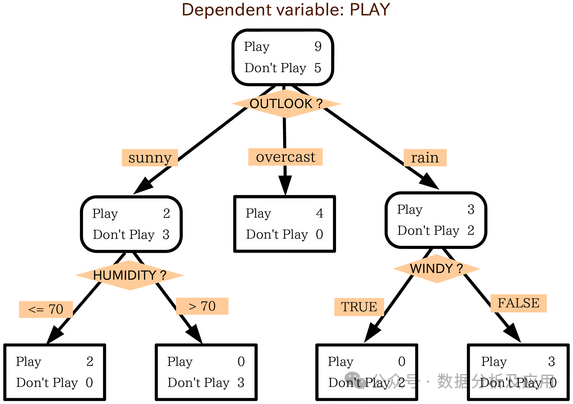
算法历程：决策树算法最早由Ross Quinlan在1986年提出，用于解决分类和回归问题。基于决策树的集成学习模型，无疑是数据挖掘任务上的王者。

原理：决策树通过一系列的问题（即决策节点）对数据进行划分，每个划分基于某个特征的值，最终到达叶子节点得到预测结果。

训练过程：

选择最优特征进行划分（基于信息增益、基尼不纯度等指标）。

对每个划分递归地构建子树，直到满足停止条件（如所有样本属于同一类、特征用尽等）。

优点：

易于理解和解释。

可以处理非数值型数据。

对缺失值不敏感。

缺点：

容易过拟合，需要剪枝技术。

对不平衡数据敏感。

适用场景：分类问题，尤其是需要有很强的决策解释性的场景（如贷款审批、客户分类等）。

Python示例代码：

 

 

from sklearn.tree import DecisionTreeClassifier
import numpy as np

# 假设X是特征数据，y是目标变量
X = np.array([[1, 2], [1, 3], [2, 1], [3, 1], [4, 4], [5, 5]])
y = np.array([0, 0, 1, 1, 0, 0])

# 创建并训练决策树模型
model = DecisionTreeClassifier()
model.fit(X, y)

# 预测
prediction = model.predict([[2, 2]])
print(prediction)

 

 

六、k均值

 

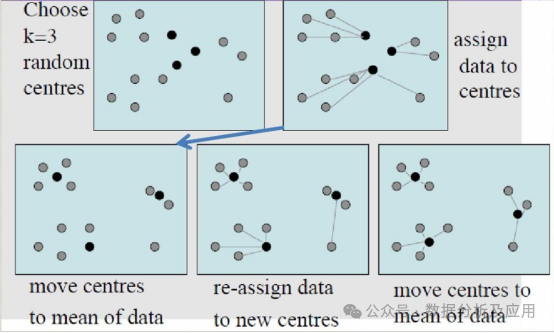
算法历程：k均值算法最早由MacQueen在1967年提出，是一种非常流行的无监督学习算法。

原理：k均值算法通过迭代的方式将数据划分为k个簇，每个簇由其质心（即簇中所有点的均值）表示。

训练过程：

随机选择k个点作为初始质心。

将每个数据点分配给最近的质心，形成k个簇。

重新计算每个簇的质心，即簇中所有点的均值。

重复步骤2和3，直到质心的位置不再发生显著变化或达到最大迭代次数。

优点：

实现简单，计算效率高。

对大数据集处理效果良好。

缺点：

需要预先设定簇的数量k。

对初始质心的选择敏感，可能导致不同的聚类结果。

对于非凸形状的簇或大小差异很大的簇，效果可能不佳。

适用场景：数据聚类、文档分类等。

Python示例代码：

 

 

from sklearn.cluster import KMeans
import numpy as np

# 假设X是需要聚类的数据
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])

# 创建并训练k均值模型
kmeans = KMeans(n_clusters=2, random_state=0)
kmeans.fit(X)

# 预测簇标签和质心
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

print("Labels:", labels)
print("Centroids:", centroids)
审核编辑：黄飞