费米气体和超导是什么关系呢？费米子的代码让电阻消失了？

金属里面自由电子构成的特殊气体，叫做“费米气体”。那么，费米气体和超导是什么关系呢？        

引入费米子的代码

超导现象与导电有关。那么，我们先来看看一般的金属遇到了电场，其中的自由电子会发生什么。  

首先，遇到电场的自由电子们，会像遇到压强的气体一样，定向地流动起来。气体的流动叫做“气流”，自由电子的运动当然叫做“电流”，这是我们一开始就知道的事情。而且，我们说过，金属的晶格非常整齐，对自由电子来说相当松快，所以金属中的电流也总是非常顺利。  

但也不是绝对的顺利。  

因为宏观世界里没有完美的存在。金属的晶格总有缺陷，图1那些格子在堆叠重复的时候，难免歪一个、多一个、少一个。而且金属当中一定会有杂质，这些杂质也会扰乱晶格的周期。那么电子定向运动的时候，就难免一头撞到某些缺陷上。这会把一部分能量转移给晶格中的金属离子，最终变成热能。

 

▲图1 晶格缺陷的某些形式。左侧的晶格有额外塞入的原子，右侧的晶格出现了扭曲。

不仅如此，热量还会让金属离子不住地颤动，所以金属的晶格绝不是像脚手架那样牢固的支架，反而会像秋水一样，来来回回地激荡着细微的涟漪，产生了许多细小的波动。  

那么，请注意，量子世界里有个著名的“波粒二象性”：粒子都可以看作波，反过来，波也可以看作粒子。包括这些晶格中激荡起来的波动，也可以看作粒子，我们称为“声子”。至于为什么会用“声”来命名它，那是因为晶格中的波动属于机械波，而机械波与声音本质上就是一回事。金属传递声音，就是大量的声子在集体运动。金属传递热量，也可以看作大量的声子在混乱运动。  

而对于我们的自由电子来说，这些声子却是些捣乱的东西。因为金属离子带有正电荷，它们波动产生的声子，当然也会带有正电荷。所以声子总会干扰自由电子的运动，这同样会把电子的部分能量消耗掉，变成热能。  

所以你看，我们虽然说金属中的自由电子像极了理想气体，但它终究还不是真正的理想气体，还是会有各种各样非弹性碰撞，会有能量的损失。于是在宏观上，我们看到通电的金属开始热，也就是电能转化成了热能，这阻碍了电能的传播，于是我们说金属也有电阻——虽然小，但不是没有。  

但是，一旦引入了那段“费米子”的代码，某些金属的电阻就会在低温下骤然消失了！  

这也就是如今常说的“超导现象”了。我们把那个让电阻消失的温度，叫做超导材料的“临界温度”，它通常都很低。比如汞的温度降到4.15K，也就是-269℃时，它的电阻就会变成绝对的0，如果用它做成一个环路通上电，那么即便没有电源，其中的电流也会永不停歇。  

这是为什么？  

因为这段费米子的代码把量子效应带进了宏观世界。  

我们说过，在理想气体或者费米气体内部，粒子之间的相互作用可以忽略不计。在很大程度上，这要归功于粒子分布稀薄，而且运动速度很快，彼此之间来不及相互作用就擦肩而过了。但是，随着温度不断降低，粒子的平均能量就会不断降低，或者说，运动得越来越慢，相会的时间越来越漫长，彼此之间的相互作用也就越来越不能忽视了。  

比如分子构成的气体，一旦温度降到沸点以下，分子就会被范德华力之类的相互作用束缚起来，凝聚成液体。类似的，当某些金属的温度降低到“临界温度”以下，其中的自由电子也会也会被一种微妙的相互作用束缚起来，然后再量子效应的支配下，发生奇特的凝聚。  

在临界温度以下，这些自由电子仍然会在晶格之中穿行。不过，自由电子带有负电荷，它运动的时候会把晶格当中的金属离子吸引过来，在自己身后微微聚拢。而这样的聚拢，正如我们刚刚知道的，会形成一个尾随自己的声子，或者说，一团局部增强的正电荷。而这又会把另外一个电子吸引过来，尾随这团正电荷。于是，以那个声子为纽带，自由电子被成对的束缚起来，构成了传说中的“库珀对”。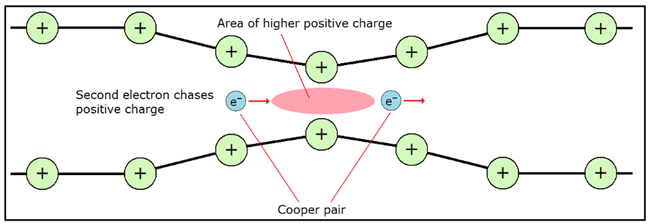  



▲图2 库珀对（Cooper pair）的原理图示：绿色是金属晶格中的金属离子，带有正电荷。右边的电子在晶格的缝隙中前进，吸引金属离子在自己身后聚拢。红色区域是因此形成的声子/局部正电荷。左侧电子因此受到吸引，尾随上去。

到了这一步，奇迹也就发生了：电子是费米子，它们组成的库珀对却是玻色子！  

这是因为库珀对由两个电子束缚而成，可以视为一个“复合粒子”。复合粒子的自旋是构成粒子的自旋之和，而构成库珀对的两个电子总是拥有相反的自旋，一个是向上的1/2，一个是向下的1/2，这样加起来，库珀对的自旋就是0，所以库珀对是玻色子——如果你搞不明白这些加法都是怎么来的，那也没关系，我们不是说过吗？不要去苛求自旋的本质，就权且把它当作一段现成的代码，任凭物理学家们算得如何辛苦，我们只需记住结论而已。  

总之，在超导体的内部，两个原本是费米子的自由电子，束缚成了一个名叫“库珀对”的玻色子。无数个这样的玻色子会在低温之下自发地同步起来，好像凝聚成了一个粒子——如果你还没有意识到这有多么奇怪，那就像满大街的人不但变得一模一样，就连动作和位置也都重合在了一起，却仍然能够占据整条大街！  

不仅如此，这个合体怪人还能到处穿行，毫无阻力的传递能量，简直像鬼魅一样。   这一切，都是因为什么呢？      

最低能量的凝聚        

我们知道，宏观上的温度降低，就是微观上的粒子动能在降低。降低的极致，就是粒子进入能量最低的“基态”，这就好比物体的高度降低，就是重力势能在降低，降低的极致，就是落到势能最低的“地基”上——这本来是很容易理解的事情。  

但在微观世界里，费米子和玻色子要把能量降落到基态上，却是大相径庭的两件事。  

对于费米子来说，非整数的自旋会让它们受到一种“泡利不相容原理”的限制。这个原理表明，任意两个相同的费米子，都不可以处在完全相同的状态上。电子就是最典型的费米子，所以任意两个相同的电子都不能处在相同的状态上。  

比如说，相同的电子不能在同一条轨道上围绕原子核运动，而必须分布在不同的轨道里，层层嵌套地摞起来。所以大多数的原子都天生的不稳定，金属原子总要丢掉最外层那几个岌岌可危的电子，就是这个缘故。

 

▲图3 元素周期表中的一个格子。注意右下角，那代表的是钙原子中的电子排布，意思是：氩（Ar）原子的电子排布是稳定的，钙原子是在氩原子的基础上，多了两个4s轨道的电子。这两个多余的电子让钙原子非常不稳定，总是想要丢掉它们，所以钙总是以+2价的阳离子形式存在。

同样，温度降低的时候，导体内的自由电子也不可以全都进入能量最低的“基态”上，这些电子只能从基态开始，逐个填入能量更高的状态，就好像砖块从地基开始，越摞越高。  

玻色子就不一样了，它们的自旋是整数，也就不会受到“泡利不相容原理”的限制，可以有无数个玻色子占据完全相同的状态。最典型的比如激光，就是大量相同的光子叠加起来，“兵合一处，将打一家”，在宏观上展现出极强的能量。同样，在温度降低的时候，系统内所有的玻色子也可以全都降落到基态上。此时，所有的粒子也都会重叠起来，行为一致，变得不可区分。  

这种大量玻色子处于相同状态的现象，被称为“玻色-爱因斯坦凝聚”，它会引发很多有趣的现象，其中最经典的就是液氦的“超流”：氦-4的原子是玻色子，所以在温度降到只有2.2K的时候，液态的氦-4会失去所有的黏性，流动起来完全没有阻力。如果你把它倒进杯子里，它就会以近乎单层原子的厚度，浸润整个杯子，从杯子里面爬出来！  

我们说，这是因为在玻色-爱因斯坦凝聚的状态下，大量的玻色子会拥有统一的行为，所以许多原本只能在微观上观察到的量子现象，就被放大到了宏观世界中来。就好像大街上熙熙攘攘，每个人的具体动作都会很难分辨，但如果行人都像国旗班的标兵一样步调一致，整齐划一，那么细小的动作也会成为引人瞩目的队形变化。  

而这也正是超导体内部发生的事情了！  

本来，自由电子都是些费米子，受泡利不相容原理的限制，不能同时进入基态。但是现在好啦，随着温度降低，某些金属内部的自由电子被束缚成了库珀对，费米子变成了玻色子，“泡利不相容”对它们的限制也就解除了。于是，自由电子以库珀对的形式，纷纷进入了那种“玻色-爱因斯坦凝聚”的状态，或者说，导体内无数的自由电子，同时达到了能量很低的基态。  

这又会怎么样呢？  

这些电子会变得像超流体一样，在运动的时候不受任何阻力，整个导体也就在宏观上失去了电阻。  

让我们用两种不同的方式理解这样的变化。  

从整体上看，我们知道，一切物体都具有波粒二象性，比如电子虽然会被视为粒子，但也同样具有波动性，有衍射的现象。电子的波长只要大于障碍物的尺寸，电子就能直接穿透过去——这在实验上是很容易观察到的现象。只可惜，在一般的温度和压强下，电子的波长都很短，它们在导体中遭遇了障碍，无论是晶格的缺陷，还是混沌的声子，都要比它们的波长更大，电子绕不过去，就只好硬撞上去，为此损失能量了。  

但是现在，电子结成了库珀对，发生了“玻色-爱因斯坦凝聚”，它们的波长就会变得非常大了。这是因为，结成库珀对之后，大量的电子全都集中在了能量很低的基态上，或者说，电子的能量变得非常“确定”，而这会触发了量子世界的另一个核心机制：测不准原理。  

测不准原理规定，粒子的位置和能量，绝不可以同时确定，当一个变得非常确定，另一个就会变得非常不确定。所以，自由电子结成库珀对之后，位置的“不确定性”就会变得非常强，换句话说，就是电子的波长变大了。  

原则上讲，这些电子的波长可以放大到微米、毫米，甚至整个导体的尺度上。大量电子的波因此叠加起来，作为一个整体感应外界的电磁场。这样大而强的波，当然可以轻松穿透导体内的一切障碍，不遭遇任何阻力了——这就是所谓的，“微观上的量子现象，放大到了宏观尺度上”。  

另一方面，我们也可以继续从微观上理解这种变化。  

量子世界与宏观世界的另一个显著区别，是量子的能量往往是“离散”的，而不是“连续”的。  

在宏观世界里，一个小球的动能从10焦耳增加到了20焦耳，我们就会当然地相信，小球动能的数值是从10开始，渐渐过渡到20的，包括11、12、13.5、15.66……两者之间的每一个数字。这样经历了所有过渡状态的变化，就是连续的变化。  

但在量子世界里，粒子的能量常常只能是某些特定的数值，不存在两者之间的过渡状态。它可以是10，也可以是20，但绝不会是两者之间的任何数值。此时，如果要粒子的能量从10增加到20，那就必须一次性地，给它提供一份刚好是10的“差额能量”，如果给它的能量小于这个差额，那么这个粒子就会拒不接受，原样退还，坚决不肯“积少成多”。这样非此即彼的变化，就是离散的。  

那么，当导体中的电子结成了库珀对，就要发生这样的离散变化了：“库珀对”是一个复合的粒子，这个粒子的能量已经处在基态上，要让它进入另一种能量状态，就要一次性地给够它差额能量。但是，超导体处在极低的温度之下，各种运动都很微弱，库珀对撞上了任何障碍物，也都只能产生很小的能量变化，给不够这份差额。  

怎么办呢？当然是坚持原则，拒绝妥协了！  

所以超导体中的库珀对，即便撞上了任何障碍，也不会因此发生能量的变化。这表现在宏观上，就是电能不会损耗，电阻消失掉了。  

现在，我们不妨做个小结：声子和电子相互作用产生库珀对，库珀对是玻色子，可以发生玻色-爱因斯坦凝聚，然后无损耗地通过晶格，这在宏观上就会表现为超导。  

这一整套理论称为BCS理论，是以他的三位提出者，巴丁、库珀、施里弗命名的。BCS理论被实验验证之后，三人也因此获得了1972年的诺贝尔物理学奖。  

但是，新的问题很快就冒了出来：BCS理论并不足以解释所有的超导现象，尤其是不能解释所谓的“高温超导”。  

简单地说，根据BCS理论，超导现象只能在接近绝对零度的时候发生。这是因为“库珀对”是一种很微弱的束缚，温度稍一升高，库珀对就会被无规则的热运动击碎，超导的性质也就荡然无存了。经计算，超导的温度上限在30K附近，也就是-243℃左右。  

然而时至今日，我们已经发现了数不清的高温超导材料。比如临界温度90K的钇钡铜氧材料，临界温度125K的铊钡钙铜氧材料，而如果配合上地心深处那样的超高压，碳硫化氢的临界温度可以达到15℃，也就是288K！——这些温度虽然都不是常规意义上的高温，但相比BCS理论预期的30K，那的确已经高得吓人了。  

更糟糕的是，这些高温超导材料大都并非金属，其中大部分都是很复杂的氧化物，常常会被视为“陶瓷”。与传统的上金属超导体非常不同。BCS理论建立在“电子-声子相互作用”上的库珀对形成机制，此时已经很不适用了，再要解释这些库珀对如何进入了那种“玻色-爱因斯坦凝聚”的状态，也变得非常棘手了。  

显然，面对高温超导，我们需要一套新的，更加普适的理论。  

但是坦率地说，我们到现在都还没有一个令人信服的回答。而这也正是当前高温超导研究的核心任务，重中之重。毕竟，理论指导实践，如果不能理解高温超导的背后机制，我们又如何发现足以应用的高温超导材料呢？  

那么，就目前而言，设法弄清楚高温超导材料中的“赝能隙”，是一个最关键突破口。      

预先配对的能隙          

不出意外的话，“赝能隙”这三个字组合起来会让你觉得陌生又晦涩，搞不好连第一个字都念不出来，但是别担心，你马上就要知道这是什么了。  

在解释超导的零电阻时，我们刚刚说过，在库珀对中，电子的能量是“离散”的。它们平时处在一种能量很低的“基态”上，只有刚巧给足了一份差额能量，才能进入稍高的能量状态上。这也就意味着，在超导体的内部，没有任何电子的能量，能够处在这两种状态之间。  

打个比方，库珀对中的电子，就好像是掉进了一个光滑紧实大坑，只有一次性地给足了能量的差额，它们才能跳出来，回到平地上，而不会有电子悬在半坑深。  

所以，当我们统计了超导体内电子的能量分布，就会发现在两个数值之间几乎没有电子，直观地留下了一道“缝隙”，这个能量分布上的缝隙，就是“超导能隙”。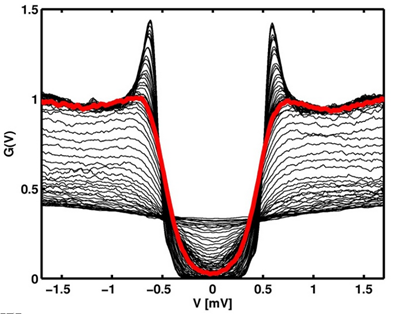  



▲图4 如果统计超导体中的电子能量分布，你会发现一个显著的缝隙。

在BCS理论适用的范围内，比如传统的金属超导材料内，能隙只在温度降低到“临界温度”之后才会出现，而且能隙一旦形成，超导现象也会立刻发生了。  

这是因为，超导能隙所对应的差额能量，其实就是两个自由电子，在结合成库珀对的过程中，发生的能量变化。在传统的金属超导材料内，自由电子本来就很多，能隙一旦形成，就标志着大量的自由电子结成了库珀对，这些库珀对会立刻建立广泛的联系，进入“玻色-爱因斯坦凝聚态”，也就足够产生超导现象了。  

而在高温超导材料内，我们却观察到了非常不同的事情：明明温度还没有降到临界温度，电子的能量分布就已经出现了能隙。但是临界温度既然没有达到，此时能隙也不会引发任何的超导现象。所以这样的能隙就不配称为“超导能隙”，我们因此叫它“赝能隙”——“赝品”的“赝”，所谓“赝能隙”就是“假的能隙”。  

假的虽然是假的，但是它给我们打开了关键的新思路：  

赝能隙的存在，似乎证明了，在临界温度以上，在超导现象出现以前，自由电子就已经结成了库珀对。那么，这就意味着，库珀对的形成，似乎还有其它不同的途径，这要比BCS理论想象得更加复杂。而且库珀对形成之后，也未必立刻形成“玻色-爱因斯坦凝聚”，其中还有一些其它的条件。  

如果我们弄明白这些细节，是不是就可以研发出更容易产生库珀对，也更容易形成玻色-爱因斯坦凝聚的材料，促成超导技术的现实应用呢？   所以我们现在的第一个问题就是：赝能隙，真的是电子形成库珀对的产物吗？  

这个解释的确非常合理，但我们不能排除其他的可能。比如另一种有力的解释认为，赝能隙与库珀对无关，只是在温度降低的过程中，电子出现了某些规律的组织方式。比如说，晶格是周期重复的，而且带有正电荷，那么在低温之下，自由电子可能会在晶格的影响下，同样呈现周期性的分布。那么电子的能量就会避开某些数值，造成赝能隙的假象。  

谁对谁错呢？只有实验才能验证了。  

但棘手的是，电子实在太小了，又处在材料的晶格之中，实在难以观察。所以就好像流体力学经常用彩色的液体代替透明的空气那样，我们不妨另外寻找一种物理模型，代替这些破朔迷离的电子。  

既然，导体中的自由电子可以看作费米气体，那么，我们最好的选择，就是另一种更易观察的费米气体了——原子构成的气态超流体。  

是的，我们不是刚刚才举过例子吗？  

超流体，也是玻色-爱因斯坦凝聚的产物。粘滞阻力在这些流体中的消失，就与电阻在超导体中的消失，都是一模一样的原理。甚至，超流体内同样可以产生库珀对：有些原子是玻色子，比如氦-4，它们可以直接在低温之下发生玻色-爱因斯坦凝聚。但有些原子，比如氦-3，就是费米子，它们不能直接进入玻色-爱因斯坦凝聚，却能在更低的温度下，两两吸引，结成库珀对，也同样发生玻色-爱因斯坦凝聚，成为超流体。  

那么，是否存在某些费米子构成的超流体，可以在超流现象发生之前，就预先结成库珀对呢？  

如果我们可以观察到这样的现象，那就很有理由触类旁通，相信高温超导材料中的赝能隙，也是电子在临界温度之上，预先结成库珀对了。那么，刚才的那一大串推测，也就顿时变得有理有据，乐观起来了。  

好的，说干就干，中国科学技术大学潘建伟、姚星灿、陈宇翱等人组成的研究团队经过逾四年的艰苦攻关，创造性地开发了动量可分辨的微波谱学探测技术。终于在今年初，他们在原子构成的费米气体发生超流现象的过程中，观察到了超流相变温度之上的赝能隙，并且最终确定了这些赝能隙是原子们预先结成库珀对时产生的。  

简而言之，我们已经间接的证明了，赝能隙的确是电子预先结成库珀对的结果。  

就这样，我们对高温超导的认识又向前迈进了一步。这虽然只是很小的一步，但对于理解高温超导材料中的库珀对如何形成，又如何发生玻色爱因斯坦凝聚，都将产生积极的作用，也为我们未来的实践，带来了更多了理论支持。    

审核编辑：刘清