基于FPGA的FIR数字滤波器设计方案

今天给大侠带来在毕业设计之基于FPGA的FIR数字滤波器设计，仅供大侠参考，话不多说，上货。

本篇介绍基于FPGA的FIR数字滤波器设计，针对毕业设计要做的基本工作有如下几点：

（一）掌握有限冲击响应FIR（Finite Impulse Response， FIR）的基本结构，研究现有的实现方法，对各种方案和步骤进行比较和论证分析，然后针对目前FIR数字滤波器需要的特点，速度快和硬件规模小，作为指导思想进行设计计算。

（二）基于硬件FPGA的特点，利用Matlab软件以及窗函数法设计滤波器。对整个FPGA元件，计划采用模块化、层次化设计思想，从而对各个部分功能进行更为详细的理解和分工设计，最终FIR数字滤波器的设计语言选择 Verilog HDL硬件编程语言。

（三）设计中的软件仿真使用开发软件Quartus II，并且利用Matlab工具进行对比仿真，在仿真的过程中，对比证明，本设计的滤波器的技术指标已经全部达标。

1.1 本课题研究意义

在现代通信信号处理领域中，随着各种精密计算和快速计算的发展对信号处理的实时性、快速性的要求越来越高。以往的模拟滤波器无法克服电压漂移、温度漂移和噪声等问题，从而带来了许多误差和不稳定因素。而数字滤波器具有稳定性高、精度高、设计灵活、实现方便等突出优点。

FPGA元器件在高速并行处理和数据传输中有独特优势，FPGA正在前端信号处理中越来越多地代替ASIC和DSP。我们需要的就是这种设计周期短，功能密度高，重组时间短的元器件。本文在FPGA元器件的基础上，实现现代FIR数字滤波器功能。并且研究多种快速的FIR数字滤波器的理论设计思想和程序设计方法。

1.2 国内外研究现状分析

1985年，Xilinx生产出了第一块FPGA元器件，由于它有着集成度高、方便易用、开发和上市周期短的绝对优势，使得FPGA器件在数字设计和电子生产中得到迅速普及和应用，发展潜力十分巨大。现在FPGA已经发展到可以利用硬件乘加器、片内储存器、逻辑单元、流水处理技术等特有的硬件结构，高速完成FFT 、FIR 、复数乘加、卷积、三角函数以及矩阵运算等数字信号处理。这样可以完成信号处理的主要技术，如中频采样、参数估计、自适应滤波、脉冲压缩、自适应波束形成和旁瓣对消等。

1.3 研究思路

通过对目前数字滤波器的几种实现方法的简单分析，本文认为基于FPGA的数字滤波器具有许多优点，本文考虑到信息技术的发展对于数字滤波器的要求越来越高，而目前FIR数字滤波器的性能还不完善，于是选择了基于FPGA的数字滤波器作为主要研究内容，通常滤波器在进行数据处理时用到了卷积运算，在设计中的解决这些乘法运算的思路是将它们转换成加减法，这是目前解决乘法运算的主流思想。设计初期在Matlab下对滤波器原理进行证明包括（零极点图、时域和频域分析图等），分析FIR数字滤波器的多种理论设计思想和窗函数选择方法，在设计后期对FIR数字滤波器的小数乘法问题进行单独论证。然后对分析出来的问题进行论证和解决，最后在Quartus Ⅱ中进行仿真验证。

1.4 相关概念说明

数字滤波器（Digital filter)是由数字乘法器、加法器和延时单元组成的一种装置。其功能是对输入离散信号的数字代码进行运算处理，以达到改变信号频谱的目的。可认为是一个离散时间系统按预定的算法，将输入离散时间信号转换为所要求的输出离散时间信号的特定功能装置FIR（Finite Impulse Response ）由线性系统理论可知，在某种适度条件下，输入到线性系统的一个冲击完全可以表征系统。当我们处理有限的离散数据时，线形系统的响应（包括对冲击的响应）也是有限的。若线性系统仅是一个空间滤波器，则通过简单地观察它对冲击的响应，我们就可以完全确定该滤波器。通过这种方式确定的滤波器称为有限冲击响应（FIR)滤波器。

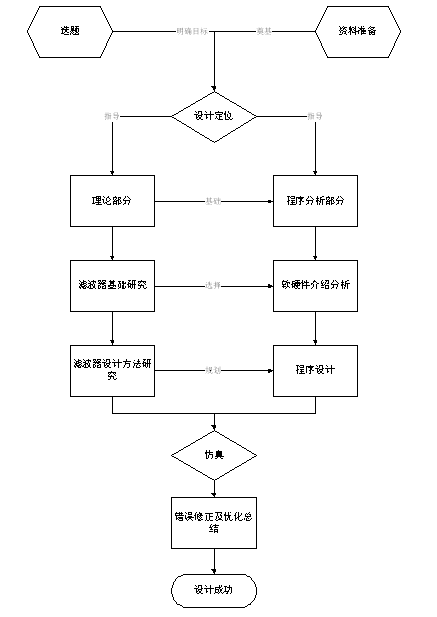
图1-1总体设计流程图

2 FIR数字滤波器的设计方法

2.1 理论部分

2.1.1  引言

数字滤波器的功能一般是用来变换时域或者频域中某些要求信号的属性，滤除信号中某一部分频率分量。经过数字滤波器的信号是让其频谱与数字滤波器的频率响应相乘从而得出新的结果。经过一个线性卷积过程，从时域上输入信号与滤波器的单位冲击响应作一个卷积和。下面是卷积定义式：

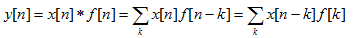（1）

LTI数字滤波器在一般情况下分为有限脉冲响应（Finite impulse response）和无限脉冲响应(Infinite impulse response)，FIR数字滤波器的设计方法和IIR滤波器的设计方法有很大的差别。因为其设计方向是选择有限长度的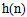，使频率响应函数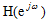满足指标。数字滤波器正在用直接的电子计算机规范和算法进行分析的方式来逐渐代替传统的模拟滤波器的RLC元器件和放大电路。

2.1.2  FIR数字滤波器的基础

首先介绍FIR数字滤波器基本原理，在如下表格中对FIR和IIR数字滤波器进行了全面的比较：

表2-1两种滤波器特点比较分析

通常情况下一般数字滤波器的N阶FIR数字滤波器基于输入信号x(n)的表达式为：

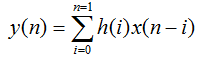
（2）

这个公式给我们了一个非常明了的直接型网络结构，该结构表现出N个乘法器，每次采样y(n)的内容是n次乘法和n-1次加法，然后做乘累加之和。如图2-1所示：

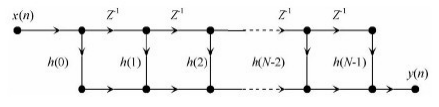
图2-1 FIR滤波器直接型网络结构

从DSP的介绍中，第一类线性相位对h(n)的约束条件：

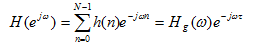 （3）

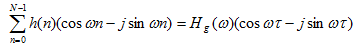(4)

由公式（3），（4）我们可以推出：

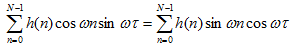 （5）

移相并利用三角公式化简得到：

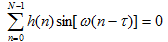 (6)

从数字信号处理学科中知道函数关于求和区间的中心（N-1）/2奇对称，于是我们要求和h(n)满足如下条件：

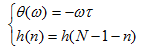
其中对应的有：

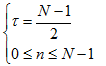（7）

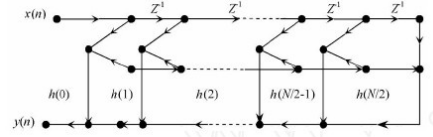
图2-2 线性相位FIR滤波器结构

若h(n)呈现对称特性，即此具有线性相位的滤波器是FIR数字滤波器。滤波器的基础网络结构可以相互进行转换。

在前面本篇已经讨论过， FPGA的实现中将对各种方法进行比较，找出最优设计方式。从而达到减少资源占有和提高系统作业速度的目的，更好的体现实时性的数字滤波器优势。

2.1.3  数字滤波器的设计原理

在数字信号处理技术的研究中，一般是使用的三种设计方法：窗函数法，FDATool直接设计法，程序编译法。本文首先使用窗函数和Matlab软件共同进行设计。

随着技术的不断发展，Matlab软件能给设计者带来的数字信号处理工作已经非常的完善和多样了，设计者可以利用Matlab软件进行数字滤波器的设计和仿真，而且还可以用这款软件进行设计的优化。数字滤波器的一般设计步骤如下：

1.指标的确定

做任何工程或者设计，设计者都必须要有一个期望的指标用来限制设计范围。在很多的实际应用中，设计者常常都是使用数字滤波器做选频的工作。因此，指标的形式一半在频域中给出相位响应和幅度。相位响应的指标形式，一半是指系统在通频带中药有线性相位。幅度指标：绝对指标，它给出对幅度响应函数的要求，一般用于FIR滤波器的设计。相对指标，以分贝值的形式给出具体限制。

2.逼近目标

设计者做高频的时候大概都有一个模式，就是首先得到技术指标，然后利用我们的技术和工具让我们的产品去逼近这个指标。同理我们首先建立以个目标的数字滤波器模型。一般情况下都是采用理想的数字滤波器模型，然后去逼近我们想要的目标数字滤波器参数。

3.计算机仿真和性能优化分析

在工作中我们发现通过（1）、（2）之后本文会得到以差分、系统函数或者冲击响应这三种方式描述的滤波器。这个时候设计者可以利用计算进行仿真，在系统中分析技术指标和滤波结果是否是希望得到的结果。

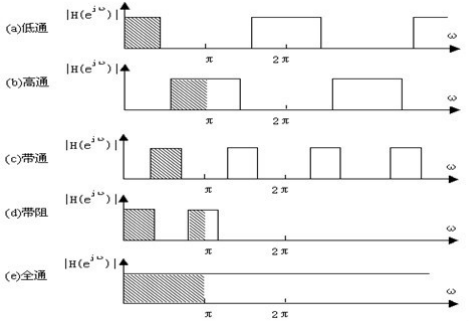
图2-3各种理想数字滤波器的幅度频率响应

2.1.4  FIR数字滤波器的理论计算方式与参数转换思想

在理论上掌握了FIR数字滤波器的基本原理之后，本文需要对设计思想进行一个多方位的论证和尝试。首先设计者设计滤波器要有一个硬性的指标，这个指标可以是直接给出最基本的数据，也有多重表现形式。于是我例举两种特殊的指标形式然后加以解决设计。然后我们分别用2种方式来设计不同指标的滤波器。接下来我首先用程序的方式来实现滤波器：

1.逼近法转换与思想

使用remez函数设计FIR低通滤波器

设计滤波器，使逼近低通滤波特性||。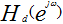

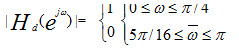
要求通带波纹 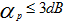，阻带衰减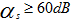，并用最小阶数实现。

绘出设计的FIR数字滤波幅频特性曲线，检验设计指标。

这个指标我们可以以如下计算方法来得出详细指标：

从给出的低通滤波特性|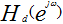|。我们可以看出设计参数f=[1/4，5/16]，m=[1，0];

dev的计算根据公式：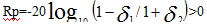

于是有,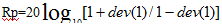

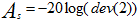
所以dev(1)，dev(2)可以被表示出来。

2.逼近法程序描述与思想

有了这几个参数我们现在就可以根据已经设定好的格式来调用函数remezord和remez函数了，于是可得如下程序。

 

 

clear;close all
fc=1/4;fs=5/16;             %输入给定指标
Rp=3;As=60;Fs=2;
f=[fc，fs];m=[1，0];            %计算remezord函数所需参数f，m，dev
dev=[(10^(Rp/20)-1)/(10^(Rp/20)+1)，10^(-As/20)];
[N，fo，mo，W]=remezord(f，m，dev，Fs);    %确定remez函数所需参数
hn=remez(N，fo，mo，W);               %调用remez函数进行设计
hw=fft(hn，512);                     %求设计出的滤波器频率特性
w=[0:511] *2/512;
plot(w，20*log10(abs(hw)));grid;        %画对数幅频特性图
axis([0，max(w)/2，-90，5]); 
xlabel('w/pi');ylabel('Magnitude(dB)')
line([0，0.4]，[-3，-3]);                   %画线检验设计结果
line([1/4，1/4]，[-90，5]);line([5/16，5/16]，[-90，5]);

 

 

3.仿真图像与结果

用以上的程序我们可以得到在Matlab中的许多参数和图像，从而进一步分析我们的设计。首先引入程序输出的幅频特性图：（如图2-4）

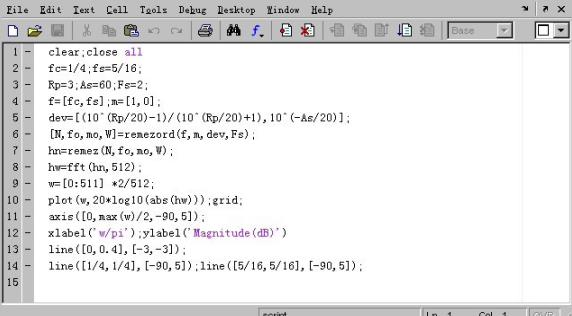
图2-4在Matlab中的程序

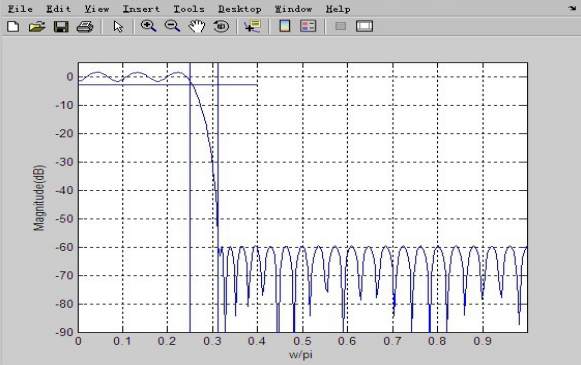
图2-5程序输出的幅频特性

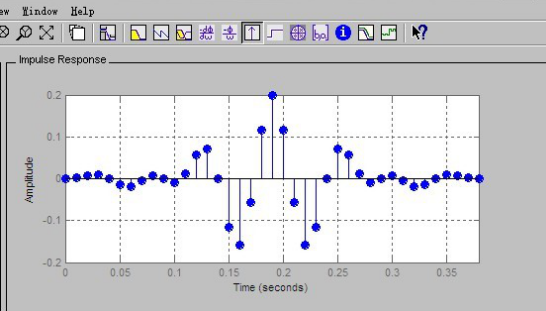
图2-6 Impulse Response

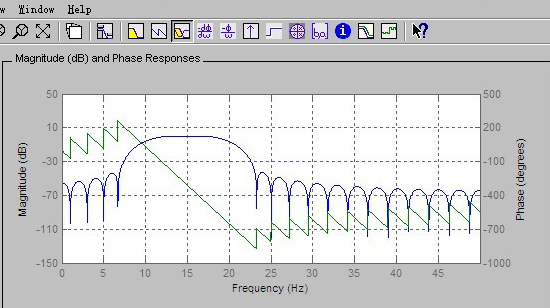
图2-7 Magnitude and Phase Responses

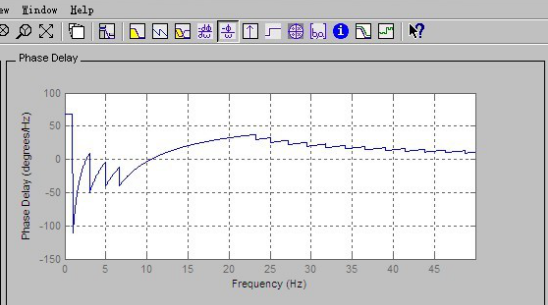
图2-8 Phase Delay

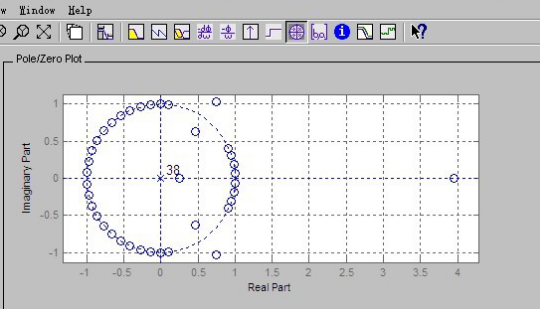
图2-9 Pole，Zero plot

结论：从上面程序运行情况分析，观察程序输出的幅频特性图中横线为-3dB，两条竖线分别位于频率π/4和5π/16。显然，通带指标有富裕，零极点图反应出大部分零极点在圆内，过渡带宽度和阻带最小衰减刚好满足指标要求。

4.窗函数选择法与规划思想

表2-2窗函数选择指标

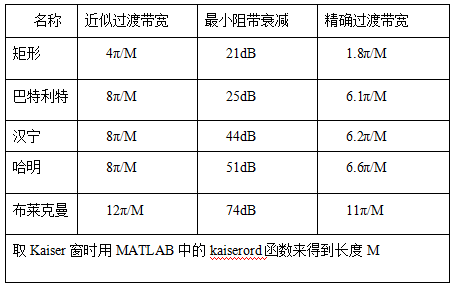
在设计指标中没有直接给出窗函数的，可以利用下面这个表格进行筛选，具体方法如下：

这个表格给出了近似过渡带宽、精确过渡带宽和最小阻带衰减，我们可以根据自己滤波器的参数来选择我们的窗函数，因为选择不同的窗函数设计出来的滤波器生成的过渡带宽度和阻带最小衰减是不同的。在这里我以一个例子来说明函数的选择方式：

用窗函数法设计FIR带通滤波器。指标如下：

高端通带截止频率：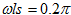

高端阻带截止频率：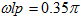

低端阻带截止频率：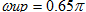

低端通带截止频率：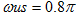

通带最大衰减  Rp=1dB

阻带最小衰减  Rs=60dB

在这样一个例子中，可以看到它明确的给出了Rs=60dB来设置窗函数类型和阶次。表格中给出的blackman窗其滤波器阻带最小衰减是74dB，再利用给出的其他参数计算滤波器阶数。表中显示窗口长度M由过渡带宽度B=0.8π-0.65π=0.15π决定，而Blackman窗设计的滤波器过渡带宽度为12π/M，则M=12/0.15=80。又因M=N+1，所以滤波器阶数N=79。 

在了解了怎么选择窗函数和计算滤波器阶数之后，本论文将针对实际FIR数字滤波器进行研究。已经给出了设计参数，下面开始利用MATLAB程序来设计这个滤波器。

5.窗函数法程序描述与思想

程序和对应的解释：

 

 

%用窗函数法设计FIR带通滤波器
clear;close all;
wls=0.2*pi;wlp=0.35*pi;whp=0.65*pi;
B=wlp-wls;              %这里是在计算过渡带宽
N=ceil(12/0.15);        %计算窗口长度
wc=[wlp/pi-6/N，whp/pi+6/N];  %设置理想带通截止频率
hn=fir1(N-1，wc，Blackman(N)); %设计滤波器参数

 

 

6.理论计算方法总结

仿真完成之后，掌握如何去利用已有的指标去设计一个滤波器，总的来说就是四项：

通过傅里叶逆变换获得理想滤波器的单位脉冲响应hd(n)。

分析给定参数，计算出滤波器的阶数，频率等等相关指标。

把已经有的参数用程序函数表达出来，利用已经有的各种内置函数架设起滤波器。

参看Matlab的输出图形和参数是否满足要求。

2.1.5  Matlab直接FDAtool设计方式解析

FDATool(Filter Design & Analysis Tool)是MATLAB信号处理工具箱里专用的滤波器设计分析工具，MATLAB6.0以上的版本还专门增加了滤波器设计工具箱(Filter Design Toolbox)。FDATool可以设计几乎所有的基本的常规滤波器，包括FIR和IIR的各种设计方法。它操作简单，方便灵活。

FDATool界面总共分两大部分，一部分是Design Filter，在界面的下半部，用来设置滤波器的设计参数，另一部分则是特性区，在界面的上半部分，用来显示滤波器的各种特性。Design Filter部分主要分为：

Filter Type(滤波器类型)选项，包括Lowpass(低通)、Highpass(高通)、Bandpass(带通)、Bandstop(带阻)和特殊的FIR滤波器。

Design Method(设计方法)选项，包括IIR滤波器的Butterworth(巴特沃思)法、Chebyshev Type I(切比雪夫I型)法、 Chebyshev Type II(切比雪夫II型) 法、Elliptic(椭圆滤波器)法和FIR滤波器的Equiripple法、Least-Squares(最小乘方)法、Window(窗函数)法。

Filter Order(滤波器阶数)选项，定义滤波器的阶数，包括Specify Order(指定阶数)和Minimum Order(最小阶数)。在Specify Order中填入所要设计的滤波器的阶数(N阶滤波器，Specify Order＝N-1)，如果选择Minimum Order则MATLAB根据所选择的滤波器类型自动使用最小阶数。

Frenquency Specifications选项，可以详细定义频带的各参数，包括采样频率Fs和频带的截止频率。它的具体选项由Filter Type选项和Design Method选项决定，例如Bandpass(带通)滤波器需要定义Fstop1(下阻带截止频率)、Fpass1(通带下限截止频率)、Fpass2(通带上限截止频率)、Fstop2(上阻带截止频率)，而Lowpass(低通)滤波器只需要定义Fstop1、Fpass1。采用窗函数设计滤波器时，由于过渡带是由窗函数的类型和阶数所决定的，所以只需要定义通带截止频率，而不必定义阻带参数。

Magnitude Specifications选项，可以定义幅值衰减的情况。例如设计带通滤波器时，可以定义Wstop1(频率Fstop1处的幅值衰减)、Wpass(通带范围内的幅值衰减)、Wstop2(频率Fstop2处的幅值衰减)。当采用窗函数设计时，通带截止频率处的幅值衰减固定为6db，所以不必定义。

参数要求：采样频率fs=100Hz，通带下限截止频率fc1=10 Hz，通带上限截止频率fc2=20 Hz，过渡带宽6 Hz，通阻带波动0.01，采用凯塞窗设计。

针对一个含有5Hz、15Hz和30Hz的混和正弦波信号已知滤波器的阶数n=38，beta=3.4。本例中，首先在Filter Type中选择Bandpass；在Design Method选项中选择FIR Window，接着在Window选项中选取Kaiser，Beta值为3.4；指定Filter Order项中的Specify order为38；采样频率Fs=100Hz，截止频率Fc1=10Hz，Fc2=20Hz。设置完以后点击窗口下方的Design Filter，在窗口上方就会看到所设计滤波器的幅频响应，通过菜单选项Analysis还可以看到滤波器的相频响应、组延迟、脉冲响应、阶跃响应、零极点配置等。设计完成后将结果保存为kaiser15.fda文件。我们可以根据FDAtool工具得到我们的滤波器相关增益。

系数转换成二进制码：

若采用乘法器，用1位整数位，1位符号位，共22位定点二进制数进行运算，负数用补码表示，由此将减法运算变成累加求和运算。各系数可用matlab编程转成二进制补码： 

 

 

/* General type conversion for MATLAB generated C-code  */
#include "tmwtypes.h"
/* 
 * Expected path to tmwtypes.h 
 * D:MATLAB7externinclude	mwtypes.h 
 */
const int BL = 39;
const real64_T B[39] = {
-0.0008969942906957，0.001248746631882，0.007070735236406，0.009180571739749，-8.354434235897e-018，-0.01457672567709，-0.01798701306701，-0.005189936475222，0.006300913248271，-5.136773213647e-018，-0.009200436084654，0.01113207796169，0.05739543087552，0.07065284310647，-2.116878167777e-017，-0.1149210109554，-0.1575671556317，-0.05691148173912，0.1151784185022，0.2，0.1151784185022，-0.05691148173912，-0.1575671556317，-0.1149210109554，-2.116878167777e-017，0.07065284310647，0.05739543087552，0.01113207796169，-0.009200436084654，-5.136773213647e-018，0.006300913248271，-0.005189936475222，-0.01798701306701，-0.01457672567709，-8.354434235897e-018，0.009180571739749，0.007070735236406，0.001248746631882，-0.0008969942906957
};

 

 

这是一个非常典型的例子，可以清晰的看到利用Matlab提供的FDAtool设计滤波器的方便与快捷。比较以上几种类型的滤波器参数，在给定的参数要求下，采用椭圆滤波器可以获得最佳的幅频响应特性，具有阶数低，过渡带窄等优点。虽然椭圆滤波器在通带也会产生波动，但考虑到波动处在可接受的范围内，仍然符合设计要求。

但由直接型传输函数表达式来实现并不实用。因此如前所说，将其分解为多个二阶传输函数的级联形式。借助Matlab 信号处理工具箱中函tf2sos(Transfer function to second- order- section)将传递函数转换为二阶级联形式。

对于是数字信号，需要对先前分析计算中分解获得的二阶子系统的滤波器系数进行量化，即用一个固定的字长加以表示。量化过程中由于存在不同程度的量化误差，由此会导致滤波器的频率响应出现偏差，严重时会使滤波器的极点移到单位圆之外，使系统不稳定。为了获得最优的滤波器系数，量化的精度也相当重要。

2.1.6 FDAtool设计模板及设计结果图

这里把上面的滤波器设计参数的总体图给出，如图2-10

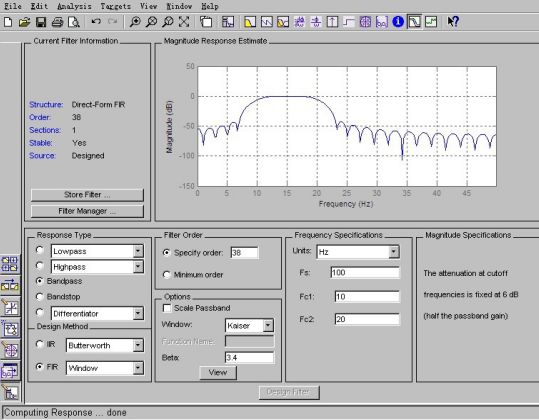
图2-10 FIR带通滤波器总体设计参数

2.2程序分析部分

根据上述FIR低通数字滤波器的原理与滤波特性，我们在上面的软件实践中已经掌握了设计数字滤波器的方法并且成功的使用Matlab/Simulink进行了设计和仿真。通过以上的过程我们可以导出一定性能的FIR滤波器频率响应与抽头系数，然后用Verilog HDL语言设计和QUARTUSⅡ仿真FIR低通数字滤波器，实现用软件描述硬件的动作及功能，应用软件来实现数字滤波器的功能和时序仿真。

2.2.1FPGA 可编程逻辑元件介绍

EDA是Electronic Design Automation的缩写，意为电子设计自动化，即利用计算机自动完成电子系统的设计。EDA技术是以计算机和微电子技术为先导，汇集了计算机图形学、拓扑、逻辑学、微电子工艺与结构学和计算数学等多种计算机应用学科最新成果的先进技术。

它与电子技术、微电子技术的发展密切相关，吸收了计算机领域的大多数最新研究成果，以高性能的计算机作为工作工具，在EDA软件平台土，根据硬件描述语言HDL完成的设计文件，自动地完成逻辑编译、化简、分割、综合及优化、布线、仿真，直至对于特定目标芯片的适配编译、逻辑映射和编程下载等工作。

可编程逻辑器PLD(Programmable Logic Devices)是ASIC(Application Specific Integrated Circuits的一个重要分支。ASIC按制造方法又可分为全定制(Full Custom)产品、半定制(semi-custom)产品和可编程逻辑器件(PLD)。前两种ASIC的设计和制造都离不开器件生产厂家，用户主动性较差。随着微电子技术的发展，设计师们更愿意自己设计专用集成电路芯片，并尽可能缩短设计周期，最好是在实验室里就能设计出合适的ASIC芯片，并且立即投入实际应用之中，在使用中也能比较方便的对设计进行修改。可编程逻辑器件就是为满足用户的这一需求应运而生的。

使用FPGA器件设计数字电路，不仅可以简化设计过程，而且可以降低整个系统的体积和成本，增加系统的可靠性。它们无需花费传统意义下制造集成电路所需大量时间和精力，避免了投资风险，成为电子器件行业中发展最快的一族。使用FPGA器件设计数字系统电路的主要优点如下:

1.设计灵活

使用FPGA器件，可不受标准系列器件在逻辑功能上的限制。而且修改逻辑可在系统设计和使用过程的任一阶段中进行，并且只须通过对所用的FPGA器件进行重新编程即可完成，给系统设计提供了很大的灵活性。

2.增大功能密集度

功能密集度是指在给定的空间能集成的逻辑功能数量。可编程逻辑芯片内的组件门数高，一片FPGA可代替几片、几十片乃至几百片中小规模的数字集成电路芯片。用FPGA器件实现数字系统时用的芯片数量少，从而减少芯片的使用数目，减少印刷线路板面积和印刷线路板数目，最终导致系统规模的全面缩减。

3.提高可靠性

减少芯片和印刷板数目，不仅能缩小系统规模，而且它还极大的提高了系统的可靠性。具有较高集成度的系统比用许多低集成度的标准组件设计的相同系统具有高得多的可靠性。使用FPGA器件减少了实现系统所需要的芯片数目，在印刷线路板上的引线以及焊点数量也随之减少，所以系统的可靠性得以提高。

4.缩短设计周期

基于FPGA器件的可编程性和灵活性，用它来设计一个系统所需时间比传统方法大为缩短。FPGA器件集成度高，使用时印刷线路板电路布局布线简单。同时，在样机设计成功后，由于开发工具先进，自动化程度高，对其进行逻辑修改也十分简便迅速。因此，使用FPGA器件可大大缩短系统的设计周期，加快产品投放市场的速度，提高产品的竞争能力。

5.工作速度快

FPGA/CPLD器件的工作速度快，一般可以达到几百兆赫兹，远远大于DPS器件。同时，使用FPGA器件后实现系统所需要的电路级数又少，因而整个系统的工作速度会得到提高。

6.增加系统的保密性能

很多FPGA器件都具有加密功能，在系统中广泛的使用FPGA器件可以有效防止产品被他人非法仿制。

7.降低成本

使用FPGA器件实现数字系统设计时，如果仅从器件本身的价格考虑，有时还看不出来它的优势，但是影响系统成本的因素是多方面的，综合考虑，使用FPGA的成本优越性是很明显的。首先，使用FPGA器件修改设计方便，设计周期缩短，使系统的研制开发费用降低;其次，FPGA器件可使印刷线路板面积和需要的插件减少，从而使系统的制造费用降低;再次，使用FPGA器件能使系统的可靠性提高，维修工作量减少，进而使系统的维修服务费用降低。总之，使用FPGA器件进行系统设计能节约成本。

2.2.2 QuartusⅡ及Verilog HDL介绍

Quartus II 是 Intel 公司的综合性开发软件，支持原理图、VHDL、VerilogHDL以及AHDL（Altera Hardware Description Language）等多种设计输入形式，内嵌自有的综合器以及仿真器，可以完成从设计输入到硬件配置的完整PLD设计流程。

Quartus II可以在XP、Linux以及Unix上使用，除了可以使用Tcl脚本完成设计流程外，提供了完善的用户图形界面设计方式。具有运行速度快，界面统一，功能集中，易学易用等特点。

Quartus II支持Altera的IP核，包含了LPM/MegaFunction宏功能模块库，使用户可以充分利用成熟的模块，简化了设计的复杂性、加快了设计速度。对第三方EDA工具的良好支持也使用户可以在设计流程的各个阶段使用熟悉的第三方EDA工具。

此外，Quartus II 通过和 DSP Builder工具 与 Matlab/Simulink相结合，可以方便地实现各种DSP应用系统；支持Altera的片上可编程系统（SOPC）开发，集系统级设计、嵌入式软件开发、可编程逻辑设计于一体，是一种综合性的开发平台。 

Maxplus II 作为Altera的上一代PLD设计软件，由于其出色的易用性而得到了广泛的应用。目前 Altera 已经停止了对Maxplus II 的更新支持，Quartus II 与之相比不仅仅是支持器件类型的丰富和图形界面的改变。Altera在Quartus II 中包含了许多诸如SignalTap II、Chip Editor和 RTL Viewer 的设计辅助工具，集成了SOPC和HardCopy设计流程，并且继承了Maxplus II 友好的图形界面及简便的使用方法。

Altera Quartus II 作为一种可编程逻辑的设计环境， 由于其强大的设计能力和直观易用的接口，越来越受到数字系统设计者的欢迎。

Verilog HDL是目前应用最为广泛的硬件描述语言。Verilog HDL可以用来进行各种层次的逻辑设计，也可以进行数字系统的逻辑综合，仿真验证和时序分析等。该语言适合算法级，寄存器级，逻辑级，门级和版图级等各个层次的设计和描述。Verilog HDL进行设计最大的优点是其工艺无关性。这使得我们在功能设计，逻辑验证阶段可以不必过多考虑门级及工艺实现的具体细节，只需根据系统设计的要求施加不同的约束条件，即可设计出实际电路。VerilogHDL是一种硬件描述语言(hardware description language)，为了制作数字电路而用来描述ASIC和FPGA的设计之用。VerilogHDL 的设计者想要以 C 编程语言为基础设计一种语言，可以使工程师比较容易学习。

2.2.3实际滤波器程序设计（11阶FIR数字滤波器）

FPGA实现FIR滤波器，首先进行指标选定和Matlab软件参数仿真，然后执行基于Verilog方法的硬件实现中用移位方法代替了乘法运算。

表2-3设计指标要求

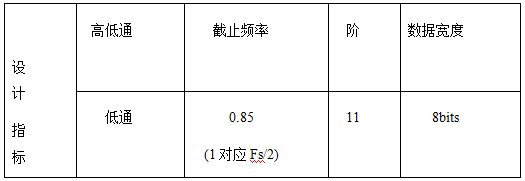
根据以上指标，利用MATLAB中的FIR滤波器系数设计命令fir1(10，0.85)所设计滤波器的系数。

表2-4 Matlab中导出的滤波器系数

MATLAB软件仿真的滤波器的抽头系数及其幅度频响特性如下图2-11所示。

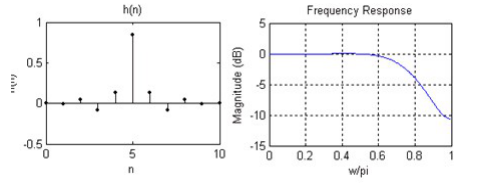
图2-11 11阶FIR滤波器的抽头系数和幅频特性曲线

可见抽头系数是奇对称的，即：

，

。

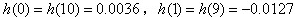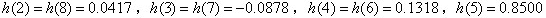FIR滤波器采用对称结构，每个抽头的输出分别乘以相应加权的二进制值，再将结果相加。同时，利用滤波器系数的及对称的特性，对输入信号 进行如下等效： 

， 

。

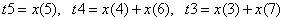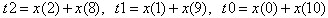2.2.4.VerilogHDL的实现

这个方法的实现中，使用了移位代替乘法运算来实现滤波器乘加的方法。由于滤波器系数都是小数，所以我们先左移7位（即放大128倍），再用相应的移位来近似这些系数，最后经过乘加运算得到结果，对这个结果再右移7位（即缩小128倍）即可得出正确的结果。各个系数的移位情况如下：其中2表示左移1位，1表示不移位，0.5表示右移1位，其他依次类推：

128×h(0)=128×0.036=0.4608=0.5-0.03125

128×h(1)=128×0.0127=1.6256=1+0.5+0.125

128×h(2)=128×0.0417=5.3376=4+1+0.25+0.625+0.03125

128×h(3)=128×0.0878=11.2384=8+4-1+0.25

128×h(4)=128×0.1318=16.8704=16+1-0.125

128×h(5)=128×0.8500=108.800=128-16-4+0.25+0.0625

这样，我们就可以把这个11阶FIR数字滤波器的输出用一下的算式得到

表2-5 Verilog方法设计FIR的实验数据

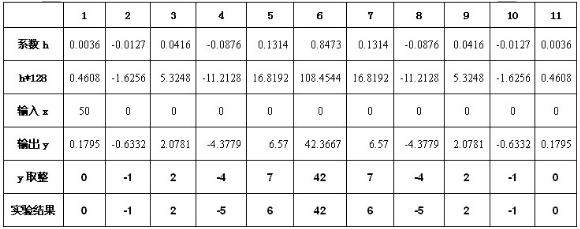
图 2-12系数放大后求SUM

计算得到结果后再将sum右移7位，即可得到正确结果。程序的功能仿真结果如下图2-12所示。

图2-13功能仿真

由上图2-12可以看出，tap0到tap10是输入x的依次延时1个时钟周期，结果sum输出相对于输入x延迟了2个时钟周期，y输出相对于sum输出延迟了1个时钟周期，这和程序设计相符合。同时，对比程序运行结果和MATLAB的计算结果（如章节开头表格所示），可知，二者结果是一致的，其中个别数据的小误差是由于移位取代小数乘法运算带来的误差。因此，程序设计是正确的。

于是，根据以上所有思想我们可以得出以下11阶FIR数字滤波器的Verilog程序如下：

 

 

module firv2(clk， x， y);
 input clk;
 input [7:0] x;
 output [25:0] y;
 reg [26:0] y;
 reg[7:0] x0，x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14，x15，x16;
 wire[21:0] acc1，acc2，acc3，acc4，acc5，acc6，acc7，acc8，acc9，acc10，acc11，acc12，acc13，acc14，acc15，acc16，acc17;
 
 reg [8:0]sxin[0:32];
 reg [5:0]i，k;
 reg [8:0]xx[16:0];
 
 parameter   c0=-21，
             c1=-8，
             c2= 22，
             c3=34，
             c4=6，
             c5=-34，
             c6=-31，
             c7=32，
             c8=87，
             c9=32，
             c10=-154，
             c11=-321，
             c12=-217，
             c13=321，
             c14=1185，
             c15=1996，
             c16=2328;  
             
  always @ (posedge clk)
    begin 
     xx[16]<=sxin[16] ;
     for(i=0;i<16;i=i+1)
     xx[i]<=sxin[i]+sxin[32-i] ;
     for(k=32;k>0;k=k-1)
     sxin[k]<=sxin[k-1]; 
     sxin[0]<={x[7]，x};
    end
  
  mult13_8 uut0(clk，c0，xx[0]，acc1); 
  mult13_8 uut1(clk，c1，xx[1]，acc2);
  mult13_8 uut2(clk，c2，xx[2]，acc3);
  mult13_8 uut3(clk，c3，xx[3]，acc4);
  mult13_8 uut4(clk，c4，xx[4]，acc5); 
  mult13_8 uut5(clk，c5，xx[5]，acc6);
  mult13_8 uut6(clk，c6，xx[6]，acc7);
  mult13_8 uut7(clk，c7，xx[7]，acc8);
  mult13_8 uut8(clk，c8，xx[8]，acc9); 
  mult13_8 uut9(clk，c9，xx[9]，acc10);
  mult13_8 uut10(clk，c10，xx[10]，acc11);
  mult13_8 uut11(clk，c11，xx[11]，acc12);
  mult13_8 uut12(clk，c12，xx[12]，acc13); 
  mult13_8 uut13(clk，c13，xx[13]，acc14);
  mult13_8 uut14(clk，c14，xx[14]，acc15);   
  mult13_8 uut15(clk，c15，xx[15]，acc16);  
  mult13_8 uut16(clk，c16，xx[16]，acc17); 


  always @(posedge clk)
    begin
      y<={acc16[1]，acc16[1]，acc16[1]，acc16[1]，acc16[1]，acc16}+{acc17[1]，acc17[1]，acc17[1]，acc17[1]，acc17[1]，acc17}
      +{acc15[1]，acc15[1]，acc15[1]，acc15[1]，acc15[1]，acc15}+{acc14[1]，acc14[1]，acc14[1]，acc14[1]，acc14[1]，acc14}
      +{acc13[1]，acc13[1]，acc13[1]，acc13[1]，acc13[1]，acc13}+{acc12[1]，acc12[1]，acc12[1]，acc12[1]，acc12[1]，acc12}
      +{acc11[1]，acc11[1]，acc11[1]，acc11[1]，acc11[1]，acc11}+{acc10[1]，acc10[1]，acc10[1]，acc10[1]，acc10[1]，acc10}
      +{acc9[1]，acc9[1]，acc9[1]，acc9[1]，acc9[1]，acc9}+{acc8[1]，acc8[1]，acc8[1]，acc8[1]，acc8[1]，acc8}
      +{acc7[1]，acc7[1]，acc7[1]，acc7[1]，acc7[1]，acc7}+{acc6[1]，acc6[1]，acc6[1]，acc6[1]，acc6[1]，acc6}
      +{acc5[1]，acc5[1]，acc5[1]，acc5[1]，acc5[1]，acc5}+{acc4[1]，acc4[1]，acc4[1]，acc4[1]，acc4[1]，acc4}
      +{acc3[1]，acc3[1]，acc3[1]，acc3[1]，acc3[1]，acc3}+{acc2[1]，acc2[1]，acc2[1]，acc2[1]，acc2[1]，acc2}
      +{acc1[1]，acc1[1]，acc1[1]，acc1[1]，acc1[1]，acc1};
    end    
  
endmodule

 

 

1.分析程序设计

使用MAC单元完成乘加运算（包括单MAC和多MAC的情况）这个方法可以利用FPGA中已有的MAC单元（像Xilinx Spartan 3E－100中有四个乘加单元），只要设计好数据运算流程，就能方便高效地实现FIR运算。使用MAC单元还有一个优点是系数可以存成系数表，可以方便地修改，这是移位方法代替乘法运算所不及的。

使用移位代替乘法运算这个方法的优点是速度快，例如11阶的滤波器，完成一次运算需要11次乘法，如果使用单MAC的话，需要11个时钟周期来完成，而使用移位方法可以在一个时钟周期完成11个乘法运算；缺点是需要另外去完成滤波系数到移位位数的换算，如果修改滤波系数的话，程序修改将会比较麻烦，同时硬件资源也要使用多一些。

t*0.125={t[7]，t[7]，t[7]，t[7:3]} t*0.125 = t/8 = t>>3; t为有符号数，所以是带符号右移，于是t>>3 ={t[7]，t[7]，t[7]，t[7:3]} 之所以这么些就是为了节省资源，提高频率

以 -4*0.5 为例  -4的原码：1000 0100B  补码：1111 1100B -4>>1=0111 1110 而符号位不能变 应用原来的位代替 1111 1110B 的原码 1000 0010B =-2

2. 对程序设计中的问题分析与总结

在最开始的设计中，本文初始计划使用乘法单元。但是在程序设计的过程中我们遇见了实数乘法的问题，程序的运行遇到了困难，在与指导老师的研究中我们发现问题出在实数乘法的问题上。在Verilog的运算中实数乘法需要特殊的小数乘法器来单元来实现。在原来的38阶滤波器的设计中出现了这样子的问题。我们使用过这样的程序：

 

 

reg  [63:0] filter_in_force [0:3344];
  reg  [63:0] filter_out_expected [0:3344];
  // Function definitions
  function real abs_real;
  input real arg;
  begin
  abs_real = arg > 0 ? arg : -arg;
  end
  endfunction //function abs_real
  // Component Instances
  filter u_filter
    (
    .clk(clk)，
    .clk_enable(clk_enable)，
    .reset(reset)，
    .filter_in(filter_in)，
    .filter_out(filter_out)
);
  initial
    begin
  // Constants
    filter_in_force [0] <= $realtobits(1.0000000000000000E+000);
    filter_in_force [1] <= $realtobits(0.0000000000000000E+000);
    filter_in_force [2] <= $realtobits(0.0000000000000000E+000);
filter_in_force [3] <= $realtobits(0.0000000000000000E+000);
…

 

 

系统无法实现real值得计算，于是这里需要我们用小数乘法器进行特殊单元的方案解决。于是我们要进行小数乘法器的设计。

3.小数乘法器介绍及在设计中的作用

随着FPGA 的发展以及相应EDA 软件工具的成熟，FPGA 在高速数字信号处理领域得到了越来越广泛的应用。而乘法，尤其是浮点乘法运算是数值计算和数据分析中最常用的运算之一。目前，多数FPGA 上可以实现整数和标准逻辑矢量的乘法，但不支持浮点乘法运算， 因此使得FPGA 在数值计算、数据分析和信号处理等方面受到了限制。本文采用适合于FPGA 实现的自定义26 位浮点数据格式，利用改进的基4Boot h 编码运算方式，以及CSA和4 - 2 压缩器综合的Wallace 树形结构，减少了部分积，使系统具有高速度，低功耗的特点，并且结构规则。在尾数的舍入中采用了基于预测和选择的舍入方法，进一步提高了运算的速度，优化了乘法器的性能。

4.小数乘法器程序设计与仿真

 

 

 modulefix_mult ( clk，rst_n，in_a，in_b，x1，x2，x3，x4，x5，x6，x7，y_out );


  inputclk，rst_n;//时钟和复位信号
  input[31:0]   in_a，in_b;//输入的被乘数和乘数
  output[31:0]   y_out;//输出的乘积
 /*寄存器类型变量 为了能更清楚的了解全处理过程，
 特地设计为输出的，不然仿真可能会被综合掉*/
 output[15:0]   x1，x2，x3，x4;
 output[0:0]    x5;
 output[29:0]   x6;
 output[31:0]   x7;
/////////////////////////////////////////////////////
 reg[31:0]   y_out;
 reg[15:0]   x1，x2，x3，x4;
 reg[0:0]    x5;
 reg[29:0]   x6;
 reg[31:0]   x7;
 always@ (posedgeclk )
 begin
 if(!rst_n )//复位时，全部寄存器变量清零
 begin
 x1<=16'b0;
 x2<=16'b0;
 x3<=16'b0;
 x4<=16'b0;
 x5<=1'b0;
x6<=30'b0;
 x7<=32'b0;
 y_out<=32'b0;
 end
 else/ 
 begin
 x1<=in_a[31:16];//截取16位被乘数，
 x2<=in_b[31:16];//截取16位乘数
 x3<=(x1[15]==0)?x1:{x1[15]，~x1[14:0]+1'b1};  //据最高位判断是否为负数，
 //若负数则把补码转成原码
 x4<=(x2[15]==0)?x2:{x2[15]，~x2[14:0]+1'b1};
 x5<=x3[15]^x4[15];//两数符号位相异或，得到乘积的符号位
 x6<=x3[14:0]*x4[14:0];//两数的数据位相乘
 x7<={x5，x6，1'b0};  //乘积由1位符号位和30位数据位及1位无关组成；
 //因为是小数，往低位生长，所以无关位放置最低位
 y_out<=(x7[31]==0)?x7:{x7[31]，~x7[30:0]+1'b1};
 end
 end
 endmodule  

 

 

小数乘法器的仿真结果如下图2-14所示：

图2-14小数乘法器仿真结果

全过程可以看成：把32位的小数截取高16位左移16位，变为16位整数相乘得到32位整数乘积后，右移32位调整无关位的位置得到32位小数，这样就可以完成早期程序中的小数乘法功能，然后来进行设计中的FPGA数字滤波器设计的优化。

在先前的设计中我们使用Matlab进行综合仿真设计，并且借助FDAtool设计出滤波器。在Quartus II 的仿真中我们发现程序无法正常的完成运行，究其原因在于小数乘法器的问题。在原来的滤波器中需要对每一个参数进行单独设置，这样会使得程序占有巨量的篇幅大大的增加了工作量和容错度。于是，我们需求另外一种方法来解决这个问题，后来我们研究了移位算法。利用移位来把小数运算转换成整数运算，这样我们的11阶滤波器程序大大减少篇幅同时也增加了程序的可读程度和稳定程度。

3 滤波器仿真滤波

3.1设置混合信号

在Matlab中进行我们设计过的FIR数字滤波器的仿真，首先我们启动Matlab中的Simulink，启动方式是直接在文本窗口中输入命令Simulink，或者点击Matlab中的快速启动按钮。

图2-15 Simulink工具窗口图

本论文模拟一个混合信号正弦波信号他包涵了10,30,60（Hz）的信号，在Matlab模拟出来是这样一个信号：

 

 

Fs=200;
t=(1:200)/Fs;
x1=sin(2*pi*t*10);
x2=sin(2*pi*t*30);
x3=sin(2*pi*t*60);
X= x1+ x2+ x3;
plot(t，X);
title('混合正弦波信号X(t)-滤波前');
grid;
Module end
//整个模拟滤波信号结束
//使用软件仿真出待滤波信号

 

 

混合信号设定之后利用Matlab工具进行模型仿真。

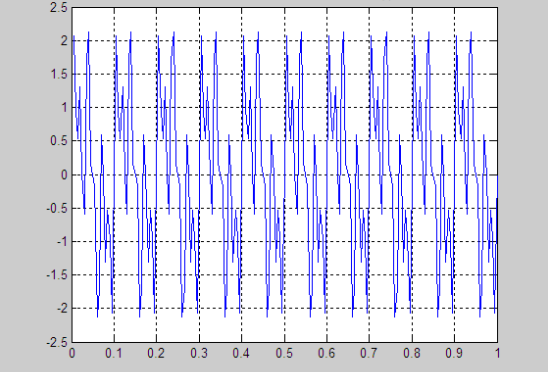
图2-16 Matlab中模拟的混合信号

然后在程序中设置好仿真模型如下图（2-17）

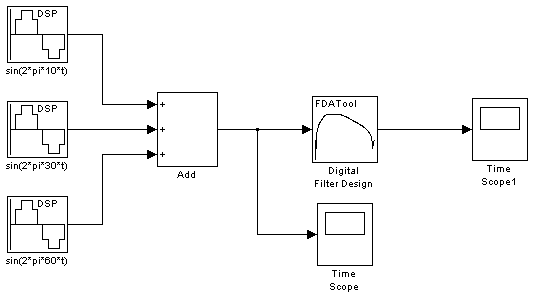
图2-17 Simulink模型仿真

3.2设置仿真参数

设置好仿真参数，对各个信号进行单独修改和设置如下图（2-18）：

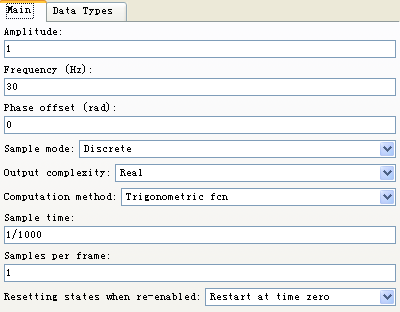
图2-18 sin(2*pi*30*t)参数模块

在主设置中，振幅(Amplitude)设置为1，                                     

频率（Frequency）设置为30Hz，                                            

输出混合为实常量，样本时间为1/1000，                                       

采样帧数设置为1帧，以下不同频率信号同理设置：

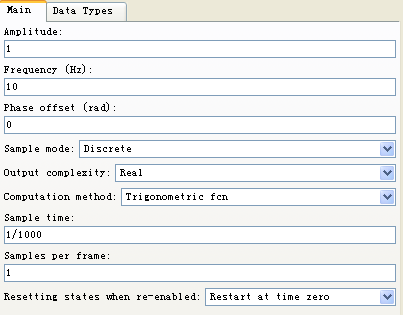
图2-19 sin(2*pi*10*t)参数模块

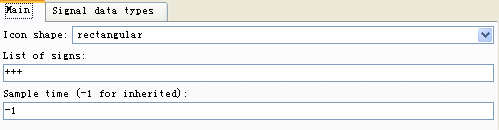
图2-20 混合参数模块

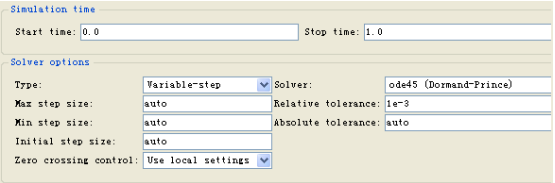
图2-21 仿真设计模块

最后来设置仿真参数：在Matlab模型窗口打开菜单[Simulation:Configuration Parameters];找到【SimulationConfiguration Parameters】对话框，设置仿真参数如下Configuration Parameters设置完成之后运行：可以直接点击模块窗口中的，开始进行仿真。输出结果如图2-22所示：

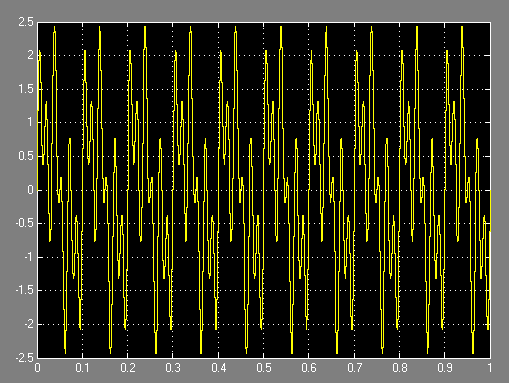
图2-22 滤波前信号波形图

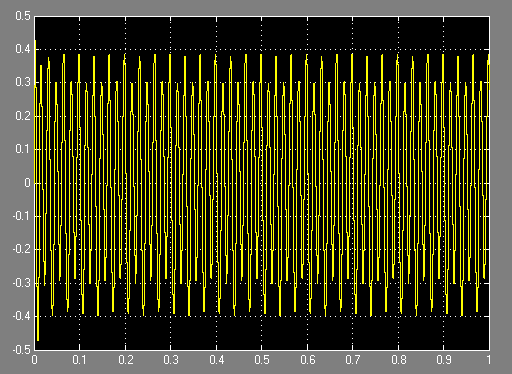
图2-23滤波后信号波形图

3.3 仿真总结

由上面的仿真结果输出图可以看出，所设计的数字带通滤波器使混合输入信号中频率为30Hz的正弦波信号通过，明显的出现了带中信号。而将频率为10Hz和60Hz的正弦波信号大大衰减，从而达到滤波效果。用Matlab Simulink仿真数字滤波器设计更加直观，操作便捷，易于分析。

4 总结与展望

4.1 设计成果总结

在理论积累和重复实践的基础上，多种滤波器设计思路已经相当成熟，设计出来的滤波器通过仿真概率高，仿真结果符合设计要求。FIR数字滤波器的设计方式选择更具有科学性和时效性，可以根据自己熟悉的软件，需要的FIR数字滤波器的精度，FIR数字滤波器的类型和滤波器阶数来灵活选择设计思路和方法。

4.2 设计心得

本次毕业设计主要包含了信号与系统，数字信号处理和FPGA方面的相关知识。设计心得总结如下：

设计路径优化 确定好所需要设计的FIR数字滤波器滤波器后，首先对其进行性能需求分析，明确FIR数字滤波器系统应该达到的各种性能指标，其次，拟定多种滤波器类型，对这些方案采用Matlab进行仿真，在这个过程中我们有许多的窗函数选择和设计方法选择，进行综合分析和比较，选择出最佳的滤波器类型作为本设计方案，然后依据其性能指标编写Matlab程序，确定二阶节系数，或者直接进行 Verilog HDL语言的编写。

系统整体思维细节决定整体，整体展现细节。我们的设计必须有系统的设计思维，把每一个细节都融入到整个系统中考虑，去发现整个FIR数字滤波器系统的主观性、完整性、稳定性和仿真功能的实现，才能让各个细节完美缝合，才能快速的完成性能优越的硬件设计。

多做设计尝试和总结，在FIR数字滤波器的设计中遇到过很多困难甚至是障碍。但是必须坚持自己的设计思路，去寻找其他的解决方法比如本论文中所提到的小数乘法器。这个本来是设计过程无法逾越的障碍，最后在不懈努力下，一样做出的小数乘法器。并且我们要善于积累和总结让障碍成为我们的另一种知识沉淀，这样我们才能融会贯通，才能更善于发现问题和解决问题。无论在什么时候，科学的道路上永远都是未知。我们应该一直坚持自己的原则，不抛弃，不放弃，这样才能在这条充满荆棘的路上走的更远！

审核编辑：黄飞