为什么说u因子能够用来比较器件之间的稳定程度呢？

(2) 无条件稳定的判决方法

稳定圆能够告诉我们，在哪些区域内，放大器是可以有条件稳定的。

不过，我们更倾向于把放大器设计成无条件稳定。K-△判据和u因子，都是判断放大器无条件稳定的方法。

其中K-△判据，共有两个条件，分别为：

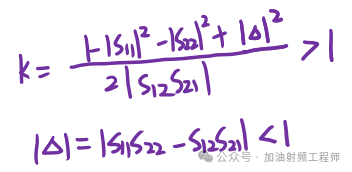
u因子，只需要一个条件，即：

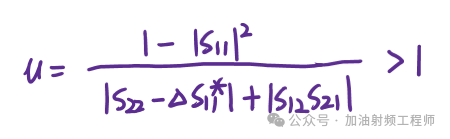
因为K-△判据判断放大器是需要两个独立的条件，所以不能用来比较器件之间哪个稳定程度更高一点。

(3) 微波工程中u因子的推导

在微波工程中，u因子的推导，是基于Γout平面进行推导的。

这对我个人来讲，是造成了一点点的困扰的，不知道你们有没有？

因为输入稳定圆是基于ΓS平面的，输出稳定圆是基于ΓL平面的，然后现在推导u因子，是基于Γout平面的。

如果把u因子也放到ΓS平面或者ΓL平面中，会不会更又助于理解？比如说下面ADS的help文件中的说明，就是把mu放在ΓS平面上的。

(4) ADS中的mu因子和mu_prime因子

从ADS的help文件中，可以知道，mu的表达式，即是(3)中的表达式，而且指出了，这个测量有这样一个意义，即表示SMITH圆图的中心离最近的output(load) stability circle的距离，也就是说，mu的几何意义，是基于 ΓL平面的。

在另一本书上的解释，有点ADS中的味道。

(5) 在另一本书上mu因子的解释

以上，分别是输出稳定圆(ΓL平面)和输入稳定圆(Γs平面)的推导。

如果想要器件无条件稳定，那么|ΓL|<1的圆应该完全处于输出稳定圆的稳定区内。

比如说，对于上式中的①，则要求，输出稳定圆不能与ΓL平面内的单位圆重叠；对于上式中的②，则要求，输出稳定圆要完全包裹住单位圆；如下图所示。

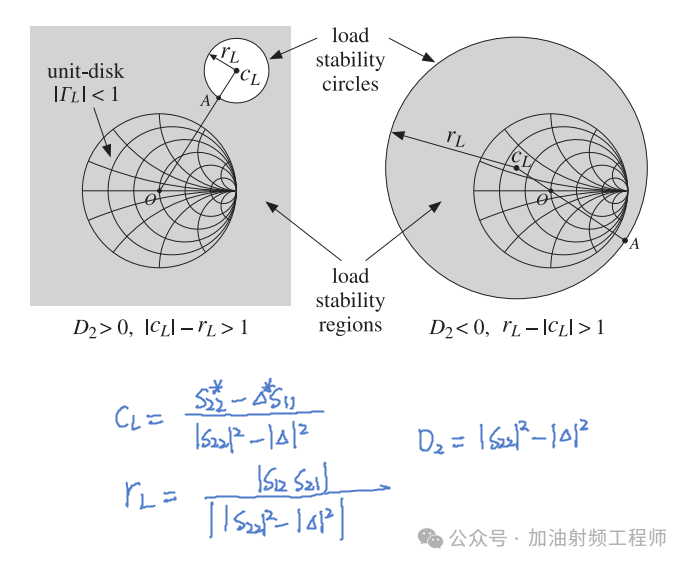
也就是说，要求：

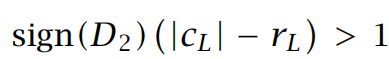
而：

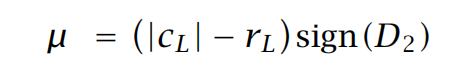
具体推导，如下：

因此，可以得出，无条件稳定的时候，要求u>1。

而且，从上图可以知道，u越大，意味着左图的稳定圆离单位圆更远了，或者意味着右图的稳定圆变得更大了，也就是说，更稳定了。

 

审核编辑：刘清