跟电源专家陶显芳学电源技术（二）：漏感与分布电容对输出波形的影响（下）

电子发烧友网讯：国内知名电源技术专家陶显芳不辞劳苦，在双节期间仍坚持为各位电源工程师或爱好者排忧解难，写出一些工程师们非常关心的技术问题和常见的电源问题及解决方法。电子发烧友网编辑现为读者整理成几部分为《跟电源专家陶显芳学电源技术》系列，内容包括：

　　1、漏感与分布电容对输出波形的影响（上）

　　2、漏感与分布电容对输出波形的影响（下）

　　3、对漏感与分布电容的影响进行数学分析

　　4、电源开关管的过压保护电路

　　5、电源开关管保护电路参数的计算（上）

　　6、电源开关管保护电路参数的计算（下）

　　7、RCD尖峰脉冲吸收电路参数计算举例：开关变压器初级线圈漏感Ls的计算

　　8、RCD尖峰脉冲吸收电路参数计算举例：尖峰脉冲吸收电容器容量的计算

　　9、RCD尖峰脉冲吸收电路参数计算举例：尖峰脉冲吸收电阻阻值的计算。

　　本文为漏感与分布电容对输出波形的影响（下），内容精彩，敬请对电子发烧友网保持密切关注。

　　当开关管开始关断时，外电路给栅极加一负电压（或低电压），通过静电感应，开关管内耗尽层中的载流子（电子）在电场的作用下会重新进行分布，相当于外电路要向耗尽层抽离载流子，耗尽层中载流子的浓度将按指数规律减小，耗尽层的厚度也将随时间增大而变小，其结果是耗尽层的电阻将随时间由小变大。这个过程，与电容被充电时，流过电容的电流由大变小很相似；所以，当开关管刚导通的一瞬间，开关管可以等效成一个理想的开关与一个电容器并联，这个电容器就是漏极和源极之间的分布电容Cds。如图5是开关管关断时，反激式开关电源的工作原理图。

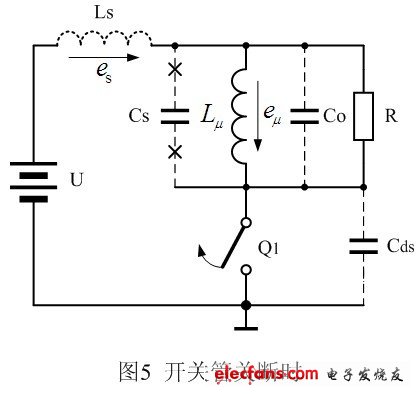
　　根据上面分析，栅极电容Cgs对开关管的导通影响比较大，容量越大，开关管的导通上升时间就越长。而漏极电容Cds对开关管的关断影响比较大，容量越大，开关管关断存储时间就越长。电容Cgs和Cds也称扩散电容，它们既具有电阻的性质，同时也具有电容充放电的特性，这种特性主要与耗尽层中载流子的浓度变化有关。

　　当电源开关管为晶体管时，Cgs和Cds分别与Cbe和Cce对应，工作原理场效应管的工作原理基本相同或相似。不过基区参与导电的载流子的密度的增加或减少，不是靠静电感应的作用，而是靠基极电流的注入。

　　由于开关管在导通或关断期间，其分布参数的性质和作用也在改变，因此，在图1～5中，要对分布电感Ls和分布电容Cs，以及Cgs和Cds组成的电流回路进行精确计算，难度是很大的。下面，我们将以很长的篇幅来对上面电路进行分析和计算。

　　在图4中，分布电感Ls和分布电容Cs可以看成是一个串联振荡回路，当开关管Q1开始导通的时候，输入脉冲电压的上升率远远大于输入电压通过分布电感Ls对分布电容Cs充电电压的上升率，此时，串联振荡回路开始吸收能量，输入电压通过Lds和Ls对Cs进行充电，流过Ls和Cs的电流按正弦曲线增长；当开关管Q1完全导通以后，Lds的值等于0，此时，输入脉冲进入平顶阶段，相当于输入脉冲电压的上升率为0，由于，输入脉冲电压的上升率远远小于分布电感Ls与分布电容Cs进行充、放电时电压的上升率，因此，振荡回路开始释放能量，振荡回路会产生阻尼振荡。

　　由于分布电感Ls和分布电容Cs的时间常数相对于励磁电感 比较小，所以分布电感Ls和分布电容Cs产生阻尼振荡的过程主要发生在开关管Q1导通和关断的一瞬间。当开关管Q1导通或关断后不久，阻尼振荡很快就会停止。当输入电压对分布电容Cs充满电后，输入电压就完全加到励磁电感 的两端。如果是反激式开关电源，流过励磁电感 的电流将随时间从0开始线性增加；如果是正激式开关电源，流过励磁电感 的电流将随时间按梯形波曲线增长。

　　在开关管Q1导通期间，由于开关管的导通内阻非常小，分布电容Cds基本上是不起作用的。当开关管Q1由导通状态转换为关断时，开关管漏极和源极之间的分布电容Cds将被接入电路中，分布电感Ls和励磁电感 将同时产生反电动势，并分别对分布电容Cds和Cs进行充、放电，电容与电感在交替进行能量交换的过程中，将产生串、并联振荡。

　　但由于励磁电感 的时间常数比Ls、Cs和Cds的时间常数大好多，因此，在产生振荡的过程中，主要由Ls、Cs和Cds三者产生作用。另外，在开关管开始关断期间，由于Cds实际上是一个阻抗由小到大，其阻抗变化过程类似于电容充电的可变电阻，它只吸收能量，而不会释放能量。因此，它在产生振荡的过程中，只对充电曲线的上升速率起影响，而对放电曲线的下降速率不起影响。

　　图6是图4和图5电路中，当开关管导通时（图4），输入电压ui通过开关变压器漏感Ls对分布电容Cs进行充电，使漏感Ls与分布电容Cs产生冲击振荡时，分布电容Cs两端的电压波形；和当开关管关断时（图5），输入电压ui与开关变压器漏感Ls和分布电容Cs、Cds产生充、放电时，电源开关管D、S极两端的波形。

　　在图6中，图6-a是电源开关管Q1导通时，输入电压ui加于开关变压器初级线圈两端的电压波形；图6-b是分布电容Cs两端的电压波形；图6-c，是电源开关管Q1漏极D与源极S之间的电压波形。

　　在t0时刻，电源开关管Q1开始导通，输入电压ui加于开关变压器两端，输入电压ui首先通过分布电感Ls对分布电容Cs充电，此时，由于输入电压ui的上升率大于电流通过分布电感Ls对分布电容Cs进行充电的电压上升率，所以，分布电感和分布电容都从输入电压吸收能量。输入电压ui在对分布电感Ls和分布电容Cs进行充电过程中，分布电容Cs两端的电压是按正弦曲线上升的；而放电时，其两端的电压则按余弦曲线下降。

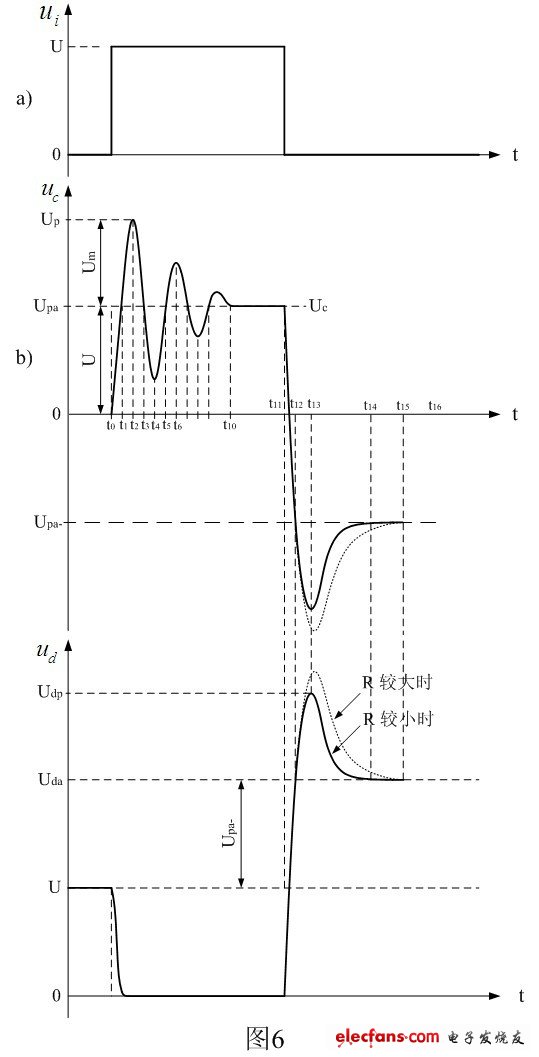
　　到t1时刻，流过Ls的电流达到最大值，同时分布电容Cs两端的电压与输入电压ui相等（或与变压器初级线圈的正激输出半波平均值Upa相等），此时输入电压ui的上升率为0，输入电压ui的上升率小于分布电感Ls对分布电容Cs充电的电压uc上升率，所以，分布电感Ls开始释放能量继续对分布电容Cs进行充电。此时，Ls在释放能量，而输入电压ui和分布电容Cs都在吸收能量，分布电容Cs都两端的电压uc继续按正弦曲线上升。

　　到t2时刻，流过Ls的电流等于0（储存于Ls中的能量被释放完毕），分布电感产生的反电动势对分布电容Cs进行充电结束，此时Cs两端的电压也达到最大值，然后Cs开始按余弦曲线对Ls和输入电压ui进行放电，流过Ls的电流开始反向，Ls开始反向储存磁能量。

　　到t3时刻，Cs两端的电压又与输入电压ui相等，电容停止放电，此时，Ls储存的磁能量将转化成反电动势es给电容Cs进行反向充电，使Cs两端的电压低于输入电压ui。

　　到t4时刻，流过Ls的反向电流等于0，Cs两端的电压达到最低值，然后输入电压又开始通过Ls对Cs进行充电，至此，分布电感Ls与分布电容Cs第一个充放电周期结束。

　　到t4时刻之后，输入电压ui对分布电感Ls和分布电容Cs进行充电的过程，以及分布电感Ls和分布电容Cs互相进行充电的过程，与t0～t4时刻基本相同。但由于在此期间，输入电压的上升率等于0，输入电压不再向分布电感Ls和分布电容Cs提供能量，因此，分布电感Ls与分布电容Cs产生自由振荡的幅度是随着时间衰减的，其衰减速率与等效电阻大小有关。

　　到t10时刻，分布电感Ls与分布电容Cs产生的阻尼自由振荡的幅度被衰减到差不多等于0，此时，分布电容Cs两端的电压等于变压器初级线圈的正激输出半波平均值Upa。关于半波平均值Upa和Upa-的计算方法及定义，请参考第一章的（1-70）和（1-71）式及说明。

　　在图6-b中，Upa为变压器初级线圈正激输出电压的半波平均值，此值与输入电压相等；Upa-为变压器初级线圈反激输出电压的半波平均值，此值与占空比相关；当占空比等于0.5时，Upa-与输入电压在数值上相等，但符号相反。

　　到t11时刻，电源开关管Q1开始关断，由于流过分布电感Ls和励磁电感 的电流通路突然被切断，其必然会产生反电动势 和 ，此二反电动势将与输入电压ui一起串联对分布电容Cs和Cds进行充电。但由于Cs两端的电压与 电压基本相等，因此，对分布电容Cds进行充电的电压正好是输入电压ui与反电动势电压 和 三者之和。

　　到t12时刻，电源开关管Q1已经完全关断，但二反电动势 和 与输入电压ui还继续对分布电容Cs和Cds进行充电，不过，此时Cds的容量已经变得非常小，因为它表示开关管内部的扩散电容，属于电阻性质，当开关管完全关断之后，阻值为无限大。

　　直到t13时刻，分布电感Ls储存的磁能量基本被释放完，二反电动势 和 才停止对分布电容Cs和Cds继续进行充电；此时，分布电容Cs和分布电容Cds的两端电压均达到了最大值，即，加到电源开关管Q1漏极上的电压达到最大值；而后，分布电容Cs又对原充电回路进行放电，并产生自由振荡，但由于电源开关管Q1关断后阻抗为无效大，其放电回路只能通过等效R和励磁电感 进行，所以振幅很快就衰减到0。图3-c为电源开关管D、S两端的波形。

　　在图6-c中，Uda为开关管Q1关断期间，D、S两极之间电压的半波平均值，Uda等于输入电压ui（ui=U）与变压器初级线圈产生反激输出电压的半波平均值Upa-之和；Udp为开关管关断期间D、S两极之间电压的峰值。Udp和Uda的值均与占空比有关，当占空比等于0.5时，Uda约等于输入电压ui（ui=U）的2倍，而Udp则大于输入电压的2倍，并且Udp的值还与漏感Ls的值大小有关，Ls的值越大，Udp的值也越大。

　　这里顺便指出，图6-b的波形是很难测量到的，因为分布电感Ls与分布电容Cs产生自由振荡的过程，基本上都在变压器内部的分布电感与分布电容之间进行，用仪器很难直接进行测量；但通过测量变压器次级线圈的波形，也可以间接测量图6-b中波形的振幅；而图6-c的波形可以直接进行测量，两者的振幅均与分布电感Ls的数值大小有关，还与等效电阻R的阻值有关。分布电感Ls的数值越大，振幅也越大，等效电阻R的阻值越大，振幅也越大。

　　当自由振荡很强时，自由振荡会通过电磁辐射的形式给周边的电路或电子设备造成EMI干扰。这一点在进行开关变压器设计时务必要注意，应该尽量减小分布电感Ls的数值。

　　下面我们进一步通过数学的计算方法来对电路的参数进行详细分析。

下节将继续报道：对漏感与分布电容的影响进行数学分析，敬请关注。

——电子发烧友网版权所有，转载请注明出处！