

LED芯片分布对散热性能的影响研究
LED散热
描述
本文针对65×65mm一面设有九颗1×1mm、1W的LED芯片,另一面为肋片的铝制散热片,利用数值法求解三维稳态导热微分方程,利用计算机专用软件计算得到不同LED芯片分布时,散热片芯片表面的温度分布,根据其温度场来分析LED芯片分布对其散热的影响。结果是:九颗芯片集中在一起散热效果最差,芯片之间的距离应达到5mm以上,其芯片温度可降低近5℃以上。
LED照明,由于节能显著,被认为是下一代照明技术。LED是冷光源,其光谱中不包含红外部分,而目前LED发光效率仅达到20%,也就是说有80%以上的电能转换成热能。如果热量不能有效散出,芯片的温度上升,会导致光效下降,光衰加剧,严重时烧毁芯片,LED芯片散热是当前LED照明发展中的一大未解决的问题。
LED芯片的散热过程并不复杂,只是一系列导热过程再加对流换热过程,温度范围不高,属于常温传热,其内的导热过程,完全可以运用计算机专用软件求解三维导热微分方程,计算分析出LED芯片中、散热片内的导热过程,以及散热片外表的对流换热,分析出整个传热过程中主要的热阻在何处,什么原因造成的,可以得到一非常清晰的解,使人们有的放矢。
但当前LED散热以及同类的半导体芯片散热,都缺少这一基础性和指导性的研究,即使有人做了,但不为众人所知。由此造成当今LED散热技术就像春秋战国时代样,出现采用热管,甚至提出采用回路热管。本文仅从LED芯片分布不同,来研究分析其对散热的影响,将对LED芯片中的设计和制造起着指导性意义。
1、计算模拟的模型
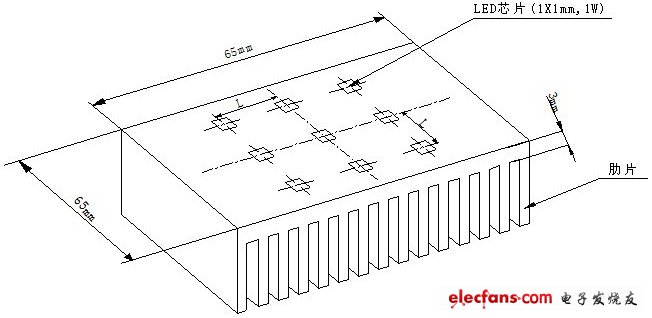
图1
如图1所示,铝制散热片的一侧面设有9颗1×1mm,1w的芯片,还有0.1mm厚导热系数取4w/(m·k)的绝缘导热层,肋片的总面积为 m2,空气对流换热系数为 =6 w/(m2·k),铝的导热系数取202 w/(m ·k)。为简化计算,不考虑肋片内的导热问题,由肋片散热面简化折算成65×65mm,对流换热系数为 85 w/(m2·k)的对流换热面。也就是求解一侧面为对流换热面( =85w/(m2·k)),另一侧为9颗芯片(1×1mm,1w)的铝块(65×65×3mm)在芯片间距不同时其内部的温度场。
#p结果#e#
求解方程:

即为三维稳态导热微分方程,通常称为拉普拉斯方程式。利用专用的计算软件求解。
2、计算结果
图2为:不同芯片间距,LED芯片所处的散热片金属表面,过中心点的温度分布。
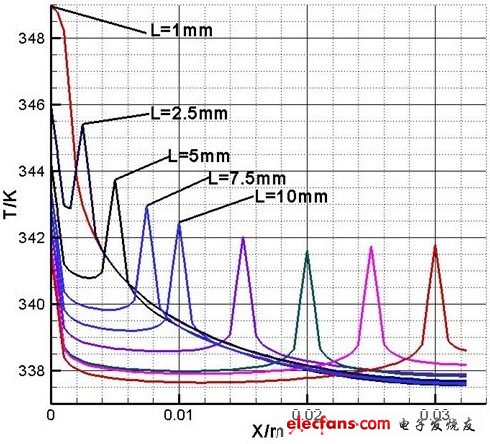
芯片间距L取1mm、2.5mm、5mm、7.5mm、10mm、15mm、20mm、25mm、30mm。
当L=1mm时,即9颗LED芯片集中在一起,之间没间隙。
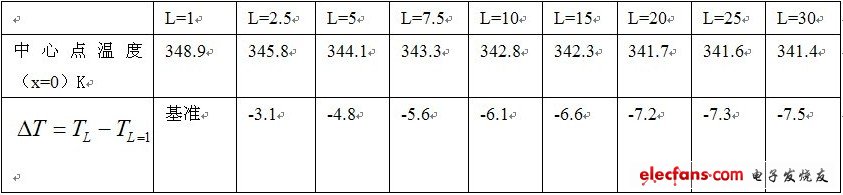
表1列不同芯片间距,LED芯片所处散热片金属表面中心点(也即温度最高点)的温度值及其差别。以上计算中环境温度取40℃(313K)。
3、分析
从图2和表1中可清楚地看:当把9颗LED芯片集中在一起(芯片间距L=1mm)时,中心点(芯片所处的温度最高点)温度最高,也就是散热效果最差。当芯片间距增加1.5mm(L=2.5mm)时,最高点温度就下降3.1℃,芯片间距增加4mm(L=5mm)时,最高点温度下降4.8℃。当芯片间距为L=7.5mm时,最高点温度下降5.6℃。当芯片间距L=10mm时,温度下降6.1℃。当芯片间距L=20mm时,温度下降7.2℃。在间距L=10mm内温度降低显著。
4、结果
(1)LED芯片分布对散热有很大影响,应该将LED芯片分散开。
(2)对于1×1mm,1w的LED芯片,芯片间距取5~10mm为佳。
-
LED阵列散热性能的研究2017-10-31 747
-
LED芯片分布对散热性能的影响2011-04-26 0
-
LED芯片分布对散热性能的影响研究2012-10-24 0
-
PCB提高中高功耗应用的散热性能2018-09-12 0
-
研究不同的模式对PCB设计热性能的影响2023-04-20 0
-
电脑机箱散热性能优化问题的研究2008-12-13 579
-
电子芯片冷却用微管道散热器的换热性能分析2011-08-18 1221
-
用三个角度来分析基于COB技术的LED的散热性能2018-01-16 6903
-
LED芯片光热分布测试案例分析2021-04-30 1770
-
普莱默之创新产品-挑战散热性能的局限2021-07-01 4112
-
LED芯片散热焦耳热分布失效分析2021-11-26 2008
-
Si二极管用的散热性能出色的小型封装“PMDE”评估-PMDE封装的散热性能 (仿真)2023-02-10 799
-
FCBGA封装的CPU芯片散热性能影响因素研究2023-04-14 2183
-
聚灿光电使用T3Ster大大提升LED芯片散热能力2024-05-07 605
-
BGA封装对散热性能的影响2024-11-20 402
全部0条评论

快来发表一下你的评论吧 !

