跟电源专家陶显芳学电源技术（三）：漏感与分布电容数学分析

　　图4中（漏感与分布电容对输出波形的影响），当电源开关管Q1导通时，设输入电压为U，流过Ls的电流为i ，流过Cs的电流为 i1，流过 Lu的电流为 i2，流过R的电流为i3 ，Cs存储的电荷为q，如果忽略Lds的作用，则列出回路方程为：

　　（11）是一个非齐次二阶微分方程。我们知道，非齐次二阶微分方程的解等于其齐次微分方程的解与非齐次二阶微分方程特解的和，其齐次微分方程为：

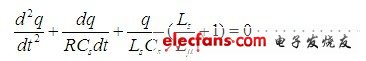　　（12）

　　（12）式表示，电容Cs充满电后，输入电压等于0时电容两端电压或存储电荷随时间变化的过程。对（12）式求解，需要先求解其特征方程，其特征方程为：

　　

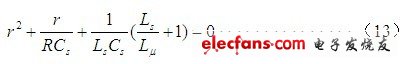
　　由此求得其特征方程的解为：

　　

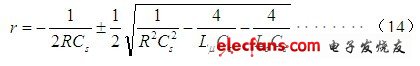
　　如果我们直接用（14）式来求解（10）式，结果将会变得非常复杂。由于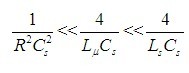， ，这也是电路产生谐振的基本条件，所以（14）式可以简化为：

　

　　由此求得：

　

　　前面已经指出，齐次微分方程（12）式仅表示电容Cs充满电后，输入电压等于0时，电容两端电压或存储电荷随时间变化的过程，即，当t = 0时， 从最大值开始随时间变化的过程。但齐次微分方程（12）式并不完全表示电容Cs充、放电的全过程，我们仔细观察（17）式便知：在LC电路中，当t = 0时，如果 为最大值，电容一定是按余弦规律放电；如果 为最小值，则电容一定是按正弦规律充电。因此，我们还需要根据初始条件来对（10）非齐次微分方程式进一步求解。

　　当电源开关管Q1导通时，输入电压才开始对电容Cs充电，Cs电容两端的电压不可能被充满电；因此，当 t = 0时，电容Cs两端的电压等于0，由此可知，（17）式中的 ，因此，（17）式可以改写为：

　

　　另外，非齐次微分方程（11）式的解应该等于齐次微分方程（12）式的通解与（11）式特解之和。

　　为求特解，我们先来观察（11）和（12）式，分析它们之间的特征，然后用代入法来求解。设（11）式的特征解为： ，则求得， ， ；把结果代入（11）式，即可求得（11）式的特解为：

　　或

　

　　　
　

　　由（21）式可以看出，等效负载电阻R的值和分布电容Cs的值越大，衰减指数因子的值就越小，而衰减系数的值就越接近1。

　　对于一个功率大约为100瓦的开关变压器，其初级线圈的分布电容大约在100~2000微微法之间，如果把次级线圈的分别电容也考虑进去，总的分布电容可能要大一倍。假设开关变压器初级线圈的等效分布电容Cs为1000P，漏感 为30uH，根据（16）式可求得振荡频率约等于900kHz。此振荡波形会迭加到变压器次级线圈的输出电压之中，使输出脉冲波形的前后沿产生严重失真，即：脉冲电压的前沿上升率降低，并产生过冲或振铃，脉冲电压的后沿产生过冲或振铃；当负载较轻时，振铃振幅很强，会造成很强的EMI辐射干扰。

　　图6-b是当电源开关管Q1导通到关断时，分布电容Cs两端电压的波形。在图6-b中，当电源开关管Q1导通的瞬间，即t = t0~t1时刻，输入电压由0突然上升到U，但由于分布电感Ls的存在，分布电容Cs两端的电压 并不能像输入电压（方波）那样，由0突然升到U，因为 电压的上升率不但要受到分布电感Ls的限制，同时也要受到电源开关管导通速度的限制，即：分布电容Cs开始被输入电压U充电时，其两端电压 的上升率除了受到L、R、C等元件的时间常数影响外，还要受到电源开关管导通速度的影响。

　　另外，LC谐振电路的振荡幅度对于正激式开关电源和反激式开关电源是不同的。对于正激式开关电源，当电源开关管Q1导通的时候，开关变压器要向负载输出能量，其等效负载电阻R的值相对比较小，衰减系数相对也比较小，因此，LC振荡被阻尼就比较厉害，振荡幅度下降就比较快。一般当第一个振荡周期过后，LC回路就很难再振荡起来。

　　对于反激式开关电源，当电源开关管Q1导通的时候，开关变压器只是存储能量，没有能量输出，因此，等效负载电阻R的值相对比较大，衰减系数相对比较大（约等于1）；此时，LC振荡的波形与等幅振荡的波形比较接近，其最大振荡幅度Um约等于分布电容Cs两端电压的半波平均值 ，即：分布电容Cs两端电压 的峰值电压Up约等于输入电压U的2倍。请参考图6-b。

　　我们从（21）式以及图3和图4可以看出：当电源开关管Q1导通时，分布电容Cs两端电压 （也是励磁电感 两端的电压），由一个最大振幅约等于输入电压U的正弦振荡电压与一个分布电容Cs两端电压的半波平均值 迭加。

　　当电源开关管Q1关断瞬间，即t = t10~t11时刻，开关变压器初级线圈的电流回路突然被切断，原来存储于 、Cs、 中的能量，只能通过等效负载R和电源开关管的内阻（分布电容Cds）进行充电来释放。

　　由于图3等效电路中的各元器件参数，在电源开关管导通期间（图4）和关断期间（图5）都不一样，因此，（21）式的计算结果只适用于开关管导通期间分布电容Cs两端电压，或通过（21）式求流漏感 的电流。而当电源开关管Q1关断时，由于开关变压器次级线圈整流滤波电路被接通（反激式开关电源），等效负载电阻R突然会变小，此时，LC振荡主要在漏感 和电源开关管的分布电容Cds组成的充放电回路中进行。

　　由于Cds为开关管内部的扩散电容，属于电阻性质，当开关管完全关断之后，阻值为无限大，漏感 产生的反电动势 只会对Cds进行充电（通过开关管的内阻释放能量），而Cds不会对漏感 进行反充电；因此，当漏感 储存的能量释放完后，其后续振荡过程也不会再发生。

　　当开关管完全关断时（图5），加于分布电容Cds两端的电压，正好是输入电压U与漏感 产生的反电动势电压 和励磁电感 产生的反电动势电压 三者之和。因此，当开关管关断时，在开关管的D、S极之间会产生很高的尖峰脉冲电压。为了防止尖峰脉冲把开关管的漏极与源极击穿，在实际应用中，一般都要对开关管采取过压保护措施。


下节将继续报道：电源开关管的过压保护电路，敬请关注。

——电子发烧友网版权所有，转载请注明出处！