使用超声多普勒方法完成管道流量测量研究（全）

　　1.1超声波流量测量发展概况

　　工业生产和科学实验都离不开对工质数量的了解或对各种物质（原料）配比的控制。为保证产品质量、进行经济核算，对单位时间内物料的输送量（流量）或某段时间内物料的总输送量（累积流量）要精确计量和控制，并要求能及时地发出反映流量大小的信号。流量测量，不管是以计量为目的，或是用于过程控制，几乎涉及所有的领域。流量测量仪表种类繁多，用超声波来检测流量是其中的一种重要方法。当超声波在流动的媒质中传播时，相对于固定的坐标系统（比如管道中的管壁）来说，超声波速度与其在静止媒质中的传播速度有所不同，其变化值与媒质流速有关，因此根据超声波速度变化可以求出媒质流速。另外也可以根据超声波在流体中的多普勒效应来求媒质流速，从而根据管径等其它已知参数计算出流体的瞬时流量和累积流量。

　　研究利用超声波测量液体和气体流量已经有数十年的历史。1928年法国的O. Rutten研制成功了世界上第一台超声波流量计，之后美国、意大利等国陆续有人研究，但都限于相位差法，进展不大。1955年，应用声循环法的超声波流量计首先作为航空燃料用流量计获得成功，随后又出现了基于时间差法和波束偏移法的超声波流量计。1958年，A.L. Herdrich等人发明了折射式超声波探头，以消除由于管壁中声波的交混回响而产生的相位失真，为换能器的管道外夹安装提供了理论依据，超声多普勒流量计也在这一时期诞生。1963年，超声波流量计开始由日本的Tokyo Keiki等人引入工业应用，但由于电子线路太复杂而未占有牢固的地位。20世纪70年代后，集成电路技术迅猛发展，高性能锁相技术的出现与应用，使得实用的超声波流量计得以迅速发展。到20世纪90年代初期日本、美国、西欧等地区超声波流量计的销售已占到流量仪表的4%~9%.20世纪90年代中期，超声波流量计世界范围的年销售台数约3.6万台，其中明渠用约占1/3，封闭管道用约占2/3，2/3中传播时间法、多普勒法、组合法分别约占81%、13 %、6%.进入21世纪，Flow Research和Ducker Worldwide的研究报告指出，全球超声波流量计（不含明渠流量计）2000年的销售达到2.4亿美元，2005年前，超声波流量计的销售还将以年均 15.3%的速度快速增长。

　　如今，超声波流量计扮演着越来越重要的角色，在供水、电力、石油、化工、冶金、煤矿、环保、医疗、海洋、河流等各种计量测试中得到广泛的应用，并在一定范围内取代了传统的差压流量计和电磁流量计等设备。超声波流量计是一个很有发展前途的方向，F.C. Kinghorn在FLOMEKO‘1996上指出［8］，“改善现有的流量测量系统或开发新型流量测量手段将给工业界带来巨大的效益，在这方面超声波流量计、文丘利管流量计及层析显像技术将会是最有发展前途的三个领域”，由此可见一斑。

　　超声波流量计主要由安装在被测管道上的超声换能器（或由换能器测量管段组成的超声流量传感器），后端处理系统，以及连接它们的专用信号电缆组成。后端处理系统在结构上分为固定盘装式和便携式两大类，以下从不同角度对超声波流量测量方法进行分类。

　　按测量原理分类：封闭管道用超声波流量测量原理有5种：传播时间法、多普勒效应法、波束偏移法、相关法和噪声法。

　　按被测介质分类：有气体用和液体用两类。

　　按换能器安装方式分类：有可移动安装和固定安装（短管式和插入式）。

　　按声道数分类：有单声道、双声道、四声道以及多声道等类别。

　　课题研究的超声多普勒流量测量方法自诞生以来，已逐步发展成为超声波流量测量的一个重要方向。超声多普勒流量计适用于测量含有适量能反射超声波信号的颗粒或气泡的液体，如污水、工厂排放液、脏流程液、农业用水、泥浆、矿浆、非净燃油、原油等，除非清洁液体中引入散射体（如气泡）或其流动扰动程度大到能获得反射信号，通常不适用于清洁液体。

　　与差压流量计和电磁流量计等各种传统的流量测量方法相比，超声多普勒流量测量方法具有以下显著特点：

　　（1）可以将检测元件置于管壁外而不与被测流体直接接触，不破坏流体的流场，没有压力损失；

　　（2）外夹式超声多普勒流量计的安装、检修均不影响管路系统及设备的正常运行；

　　（3）超声多普勒流量测量精度受流体温度、压力、粘度、密度等参数的影响小；

　　（4）尤其适合替代电磁流量计来测量腐蚀性液体、高粘度液体以及非导电性液体的流量；

　　（5）多声道技术可缩短要求的直管段长度而仍然能保证较高测量精度；

　　（6）可以从厚的金属管道外侧测量管内流体的流速，无需对原有管道进行任何加工，尤其适合应用于大管径、大流量场合。

　　相对传统的流量计，超声多普勒流量测量方法特点比较突出，适合多种工况条件和液体类型流量的测量，在工业流量测量中具有广泛的应用前景。近年来，随着电子技术和信息技术的飞速发展，超声波流量测量的技术水平有了很大提高，但研究重点非常明显地集中在血流测量等医学领域，超声波工业管道流量测量方面的研究相对较少，且主要集中于时差式流量测量（以天然气流量测量最为突出），在多普勒方法方面的研究不多，导致现有工业管道用超声多普勒流量计的性能普遍不高，存在以下缺点：

　　（1）不能判断流速方向；

　　（2）低流速测量困难；

　　（3）动态响应速度慢、实时性差；

　　（4）基本误差一般为±（1%～10%）FS，重复性为0.2%～1%，相对时差式超声波流量计、质量流量计、电磁流量计等其它流量计而言精度比较低。

　　这些缺点极大限制了超声多普勒流量计的推广和使用。目前超声多普勒流量计一般只在一些特殊场合下使用，比如便携式测量、明渠流量测量、超大管径流量测量等。

　　1.2超声多普勒流量测量研究进展

　　1.2.1多普勒流量测量模型

　　超声多普勒流量测量技术在过去的几十年中得到不断发展，出现了多种测量模型，本章概括为分为连续波多普勒（CW Doppler）模型 、脉冲波多普勒（PW Doppler）模型、伪随机多普勒模型和调频多普勒（FM Doppler）模型 四种。CW Doppler流量测量采用收发分离的换能器，它们分别连续不断地发射和接收超声波信号并进行后续处理，这种测量模型一般用于平均流速和流量的测量，详细原理见本文4.2小节，本章主要介绍后面三种模型的研究进展情况。

　　（1）PW Doppler模型

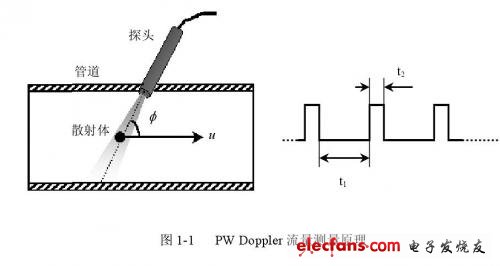
　　PW Doppler可采用收发共用的换能器，进行间断式的脉冲发射，并作时间的门控式（Time-Gate）选通接收，测量原理如图1-1所示。

　　超声换能器在起始时刻t0发射一串超声脉冲，并延迟一段时间1 t后接收超声回波信号，选通时间2 t决定了采样的回波信号长度，对应于取样分析的散射体样本大小，散射体样本在超声波传播方向的长度为：

　　

　　

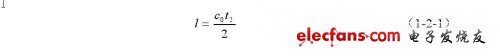
　　式中c0为流体中的声速。散射体距离管壁的径向位置为：

　　

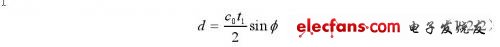
　　根据多普勒效应，对时间长度为t2的取样回波信号进行频谱分析，得到散射体速度：

　　

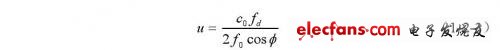
　　式中fd为散射体样本的多普勒频移，f0为发射信号频率。

　　通过改变延迟时间t1和选通时间t2，可得到超声波传播途径上任意位置的任意大小散射体样本的速度，从而可以测量流体在超声波传播方向上的流速分布。但这种方法存在一些缺点，如图1-1，定义PRF为选通时间的脉冲重复频率，由于PW Doppler流量测量可以检测出的最高多普勒频移只能是脉冲重复频率的一半，因此PW Doppler方法能探测的最大深度为：

　　

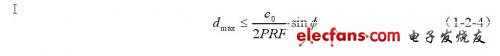
　　能够测量的最大流速为：

　　

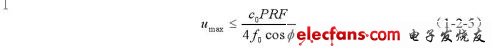
　　并且最大探测深度和最大流速之间相互制约：

　　

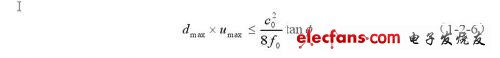
　　由于上述这些缺点，PW Doppler方法近年来逐步被一种新的时域相关技术所取代。

　　（2）伪随机多普勒模型

　　伪随机超声多普勒流量测量模型的原理如图1-2所示。

　　

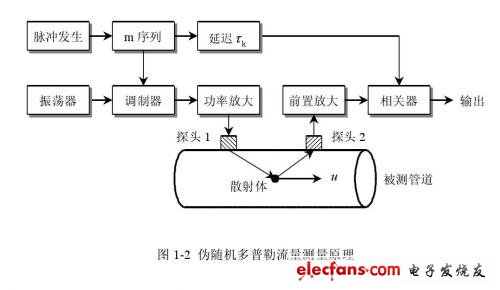
　　振荡器产生高频正弦波sinω0t，它被伪随机信号调制并功率放大后成为发射信号st（t）：

　　

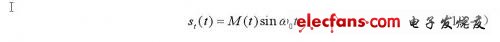
　　式中M（t）是m序列二进制伪随机码。st（t）遇到第i个散射目标后返回到接收探头的时间设为（t-τi），于是接收探头接收到的回波信号为：

　　

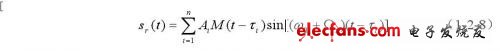
　　式中Ωi为第i个目标的多普勒频移。m序列经延迟τk后为M（t-τk），与回波信号经相关器解调后得到：

　　

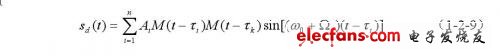
　　由m序列自相关函数的性质可知：

　　

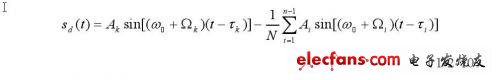
　　如果随机序列的N值相当大，则上式第二项可以忽略，即：

　　

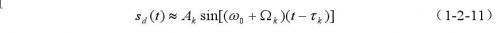
　　这样，调节延迟时间τk就可以选通不同深度的运动目标进行分析。

　　伪随机多普勒流量测量方法与CW Doppler和PW Doppler方法相比较，其可以克服CW Doppler方法没有距离选择性以及PW Doppler方法的最大测量距离和最大可能测量速度受限制等缺点。

　　（3）FM Doppler模型FM Doppler流量测量一般采用线性调频方法，如图1-3所示。

　　

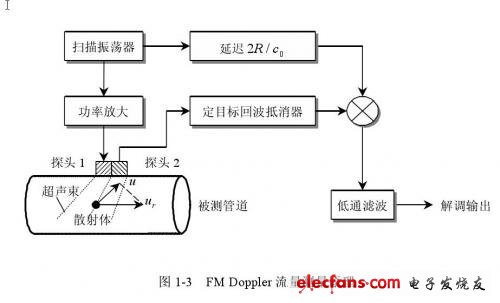
　　线性调频的扫描振荡器产生频率从f1到f2的线性调频信号：

　　

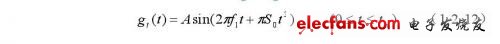
　　式中tm为扫频信号长度，扫频速率

　　

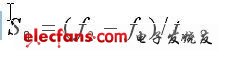
　　设散射质点位于收发换能器的声束轴线上，与换能器的距离约为R.在开始发射t =0时刻，运动质点与换能器的距离为r，运动速度在超声波传播方向上的分量为u，则发射信号经散射质点反射回到接收换能器的时间为：

　　

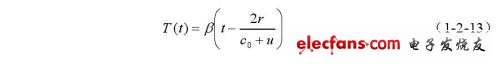
　　式中

　　

　　则接收到的信号可以表示为：

　　

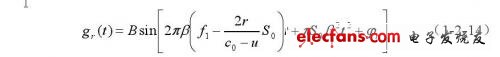
　　式中：B包含了反射系数及发射幅度等各种幅度因子，并假设换能器具有平坦的频响，传播媒质均匀且无传输损耗。送入乘法器的复参考信号为延迟了td=2R/c0的发射信号：

　　

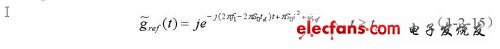
　　乘法器的输出经低通滤波后得到解调信号，该解调信号的相位有两部分，一部分是和f1，s0，u，R等系数有关的多普勒频率偏移量，另一部分是与u成正比的扫频分量，其扫频速度为：

　　

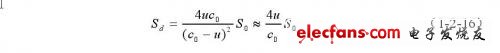
　　Sd正比于散射体运动速度，因此对解调信号进行频域或时域分析，即可得到散射体速度的估计。

　　上述四种多普勒流量测量模型中，CW Doppler模型在传统工业管道超声多普勒流量计中得到了广泛应用，而后面三种模型方法相对CW Doppler模型而言较为复杂，主要应用于医学领域，目前已有人研究将这些方法应用到工业管道流场分布和流量的测量，但离产品化还有一定距离。

　　1.2.2多普勒信号解调方法

　　CW Doppler流量测量中换能器接收到的信号可认为是多个多普勒频移成份的叠加，表述为：

　　

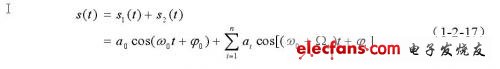
　　式中ai为频移分量幅值，Ωi为频移分量的频率，φi为频移分量的初始相位，s1（t）为经管壁、衬里等非运动介质耦合到接收探头的信号。

　　多普勒信号解调的目的在于提取频移信息，理想的解调应当取得正比于

　　

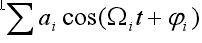
　　的输出。目前常用的解调方法有振幅检波、鉴频、鉴相及乘法器检波等四种，但由于s（t）受多普勒频移成分的非线性调制，振幅检波、鉴相检波两种解调方式将产生失真，鉴频检波输出的电压幅值中将包含与频移Ωi成正比的量，也不可取。乘法器检波用参考信号cosω0t与接收信号s（t）相乘，再用低通滤波器滤除高频分量，得到输出：

　　

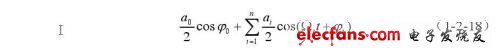
　　这种方法得到的输出没有引起失真，因此在传统的工业管道超声多普勒流量计中得到了广泛的使用。

　　1.2.3流速方向信息提取

　　现有工业管道超声多普勒流量计均不能判断流速的方向，在医学血流测量领域，流速方向信息的提取主要有时域法、频域法和相域法，分别介绍如下：

　　（1）时域法

　　基本原理是将接收到的超声多普勒信号s（t）同时送入两个乘法器，分别与有一定相位差β0的两个同频信号cosωot和cos（ω0t +β0）相乘，再低通滤波除去高频分量，于是得到第一路的输出为：

　　

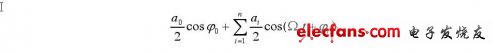
　　第二路的输出为：

　　

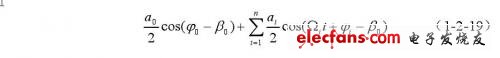
　　若血流方向为正，则Ωi》0 ，第一路输出的相位超前第二路输出的相位；若血流方向为负，则Ωi《0，第二路输出的相位超前第一路输出的相位。因此比较两路输出在时间上的先后就可以检测出血流的方向信息。

　　（2）频域法

　　超声波经血流散射后，其频谱位于发射频率ω0的两侧。血流方向为正时，回波信号频率高于ω0，成为上边带；血流方向为负时，回波信号频率低于ω0，成为下边带。频域法方向检测的关键是制作性能优良的高频上、下边带滤波器分离频谱的上下边带，使得正、反向血流信号分别在两个通道中输出

　　（3）相域法

　　假设超声多普勒回波信号表示为：

　　

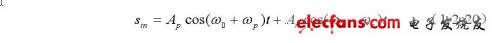
　　式中脚标p，n分别表示正向和反向血流。

　　相域法分离正、反向血流信号的框图如图1-4所示。

　　

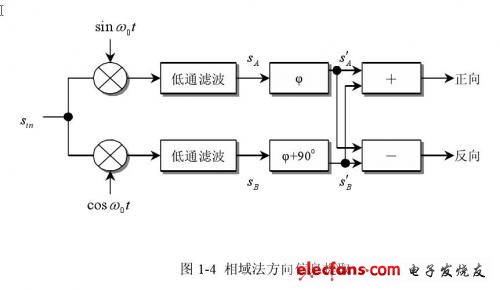
　　用两个同频正弦正交信号对输入信号进行解调，并低通滤波除去高频分量后得到：

　　

　　经过两个全通移相网络，得到：

　　

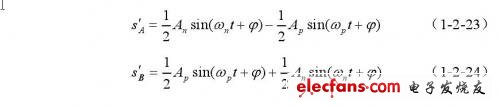
　　正向输出为：

　　

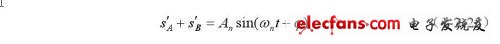
　　反向输出：

　　

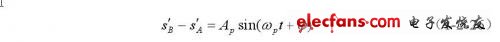
　　这样就完成了正、反向血流信号的检测和分离。相域法需要保证两路通道中低通滤波器和移相网络增益的严格对称，实现起来比较复杂。

　　1.2.4频谱估计方法

　　传统超声多普勒信号的频率估计常采用零交叉计数法和快速傅立叶变换法（FFT）等经典谱估计算法，这些方法存在频率分辨率低，旁瓣泄漏严重等缺点。为克服这些问题，以参数模型为基础的现代谱估计方法得到了很大的发展，并在超声多普勒血流测量中得到很好的应用。参数模型法的思路是假定需分析的多普勒信号 x（n）（n= 1，2，。..，N ）是一个输入序列u（n）激励一个线性系统H（z）的输出，由已知的x（n）估计H（z）的参数，再由H（z）的参数来估计x（n）的功率谱。x（n）和 u（n）之间有如下的输入输出关系：

　　

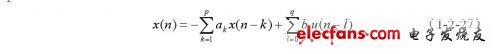
　　式中b0 =1，若b1，b2，。..， bq全为零，则为AR（Autoregressive）模型；若a1，a2，。..，ap 全为零，则为MA（Moving Average）模型；若a1，a2，。..，ap， b1，b2，。..，bq 不全为零，则ARMA（Autoregressive Moving Average）模型。当参数模型为AR模型时，H（z）和功率谱Px（ejω）分别表述如下

　　

　　式中σ2为u （n）的方差。AR模型的系数求解算法有自相关法、Burg算法和改进的协方差（MCOV）算法等。采用MCOV算法时，AR模型的参数可以通过求解改进的协方差方程组进行估计：

　　

　　

　　式中fs是采样率。采用这种方法时，计算复杂性会随着阶次p的增加而增大。确定阶次p的常用方法有最终预测误差准则和信息论准则等。血流分析中，根据多普勒信号的特点，一般取阶次p=4。

　　1.2.5数字信号处理技术

　　DSP器件采用并行的总线结构，运算速度快、集成度高，于20世纪80年代初出现，到20世纪90年代中后期开始高速发展，近年来在超声多普勒血流测量领域受到高度重视，被广泛用来分析多普勒信号的频谱。另外，在数字信号处理中也有人用FPGA（Field Programmable Gate Array）来实现一些比较固定的算法，如FFT、FIR（Finite Impulse Response）滤波等。

　　采用高速DSP以及FPGA等器件的系统设计方法使得传统基于硬件的设计转移到基于软件设计，信号处理研究的重点在很大程度上可以放到软件算法上来，从而在抗干扰、提高检测精度、实现仪器的智能化等方面具有传统基于硬件设计方法所没有的若干优点。另外，由于器件的高速性，测量方法也由最初的非实时应用转向高速实时应用。

　　1.2.6多普勒谱峰搜索方法

　　CW Doppler流量测量的多普勒信号具有以下特点：

　　（1）由于换能器具有指向性，在流场中发射换能器和接收换能器的两个指向性波束重叠区域（取样域）

　　内粒子所反射的信号将以不同的幅度和相位在接收换能器上进行叠加，由于这些粒子的速度有差异，反射角度不同，产生的多普勒频移也不一样，叠加的结果使得多普勒信号频带加宽，形成以对应管道中心轴线上最大流速的多普勒频率为谱峰的左右两个边带；

　　（2）由于取样域的扩展以及声衰减的影响，导致频谱中低频成分的增加，使得频谱的实际峰值位置向低频方向偏移；

　　（3）工业管道流量测量中，管道一般较粗，换能器只能在流场中的局部区域取样，这样多普勒信号的频谱不能反映管道截面的完整状况。

　　传统超声多普勒流量测量技术在估计流体管道截面上的平均流速时采用零交叉计数法或计算全频域多普勒平均频率的方法，由多普勒信号的上述特点可知，这些方法将会产生很大误差。而用搜索管道中心轴线上最大流速对应的多普勒谱峰频率来代替传统的方法将可以有效减小这些误差，二次平均谱峰搜索方法因此得到发展并在一定程度上修正了多普勒谱峰的偏移 。该方法先求全频域的多普勒平均频率，然后在平均频率以上的高频有效区域再求一次平均频率，将得到的平均频率值作为近似的多普勒谱峰频率，可以修正多普勒低频偏移的影响，但是增大了运算量，实时性变差。

　　另外在医学血流检测中还有相位估计法和Teager估计法等 ，这些算法的一个共同特点是运算量均比较大、实时性差。因此无论是在工业管道流量测量还是在医学血流检测中，均缺少一种运算量小、实时性好的谱峰搜索方法。