Allan 方差理论及测量方法

Allan方差起初是为了评估原子钟振荡器的稳定性而提出的，它提供了在不同时间尺度上频率稳定性的可靠测量，而标准偏差等统计量却没有考虑到这一点。在本白皮书中，我们将回顾 Allan 方差的数学基础，并分享Allan 方差及其相关参量如何在振荡器表征等实际应用中成为精确分析时间序列数据的有用工具。

 

 

利用Moku 我们可以执行Allan 方差测量，Moku 是一种基于 FPGA 的设备，它包含了一整套可重构的测试测量仪器。相位表 是Moku上开发的高精度数字相位测量仪，我们可以超精确地记录输入周期信号的相位、频率和振幅数据，也可以实时地计算和绘制 Allan 方差统计数据。

 

 

Allan 方差由来

您的系统稳定性如何？有许多工具可以用来解答这个问题。1960年 David W. Allan 在在美国国家标准技术研究院（当时称为国家标准局）研究光学时钟时发明了一种全新的工具 [1]。

 

 

Allan 发现，随着样本数量增加，现有的统计指标（例如标准差）对于特定噪声源会出现偏差。这促使他开发了一种新的时域计量方法，今天该方法以他的名字命名。

 

 

由于 Allan 当时研究光学时钟，所以为原子频率钟标准开发了 Allan 方差。因此，该主题的讨论经常仅限于该领域的术语，特别是在表征振荡器的频率稳定性方面。

 

 

但是，Allan方差可以针对任何时间序列进行计算。该序列可以代表信号自身，像温度传感器的输出信号，或其任意属性（如频率、相位、幅度等），并以恒定的速率进行评估。因此，Allan 方差从通信 [2] 到导航 [3] 的各种应用中备受青睐。

 

 

Moku 相位表提供了 Allan 方差作为一个数据后续处理的选项，如下方图 1 Moku:Pro 相位表所示。本说明针对首次接触的用户提供了有关该统计方法的入门介绍。

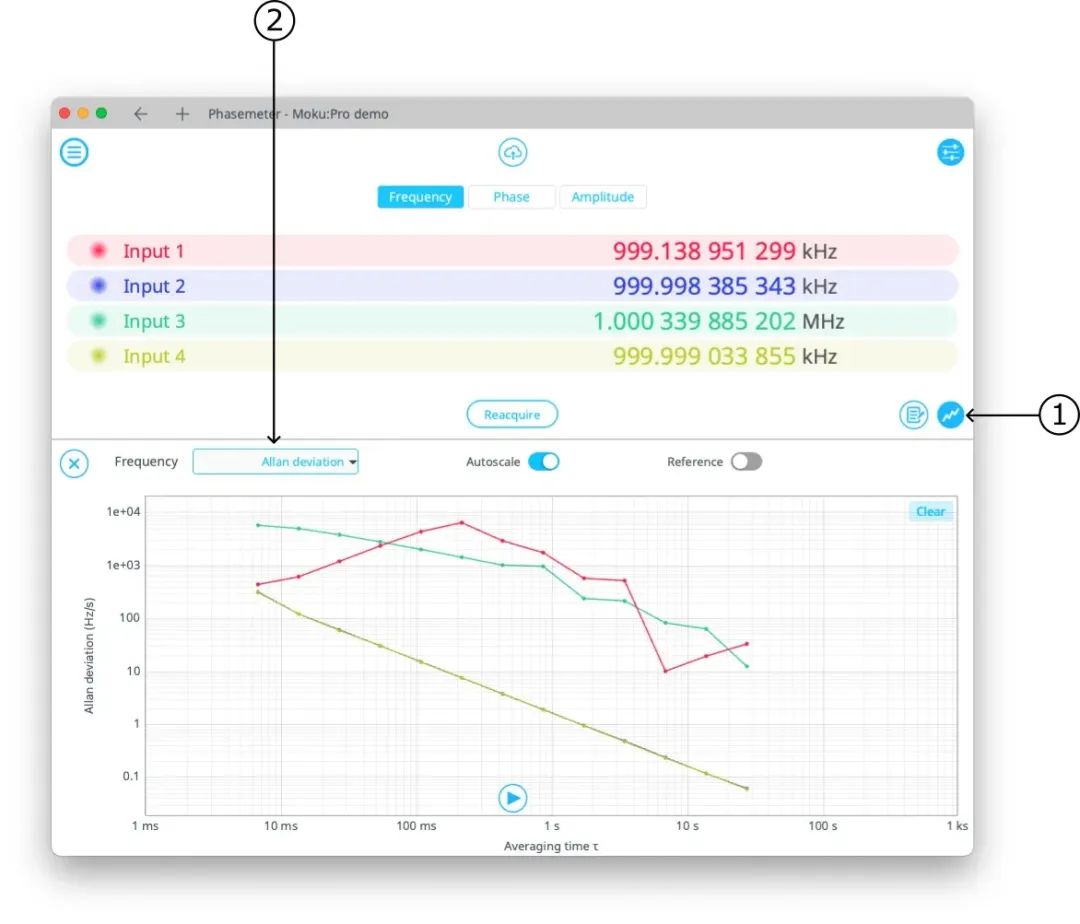图 1: 在相位表上显示 Allan 标准差（Allan 方差的平方根），首先单击数据图形显示按钮。然后从下拉菜单选择“Allan 标准差”。

Allan 方差数学运算

 

Allan 方差的基本原理是将时间序列划分为等分的部分，并考虑每等分的时间平均值与前一等分的时间平均值有何不同。如果从整个数据集来看这些差异很小，那么系统在这个时间尺度上是稳定的。

 

 

 

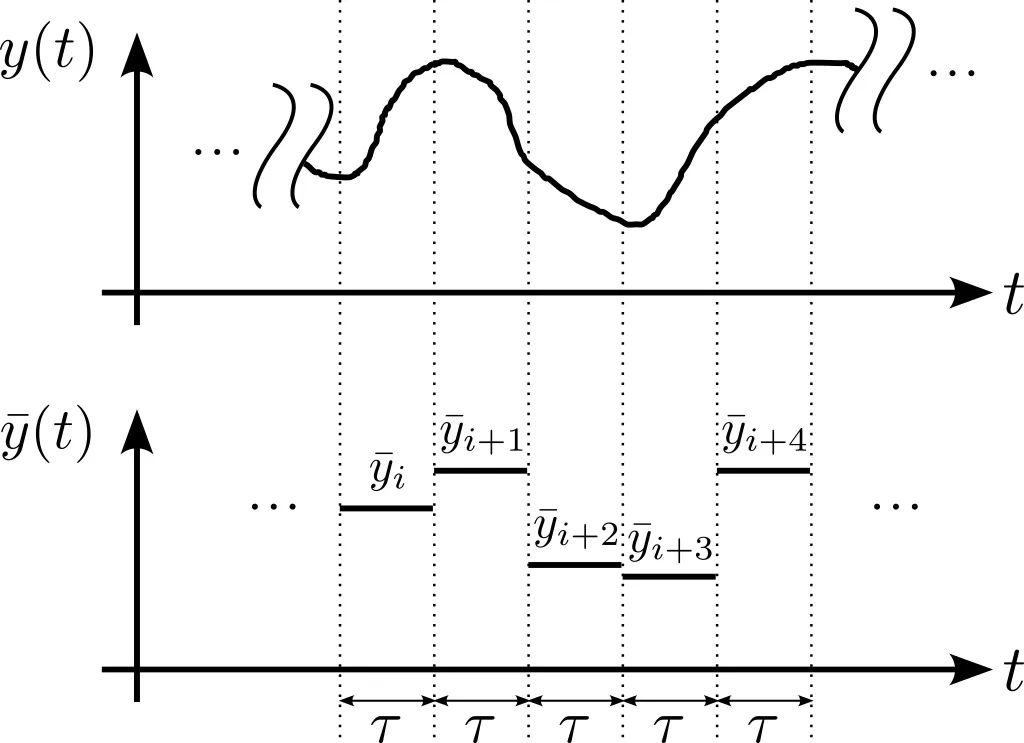
图 2: 计算 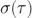第一步是将数据分割成长度为 τ 的片段并计算每一个分段 的时间平均值，。然后，我们减去连续平均值并计算这些差异的 RMS 值。将计算结果除以 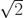得到观测时间  τ 上的 Allan 方差。

 

 

更具体地说，假定我们有一个连续的时间序列 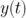，其 Allan 方差 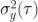定义为：

 

 

 

 

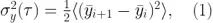
这里 <.> 表示期望值<平均值>，同时  是 y 在观测时间 τ 上的第 i 个样本的平均值（图 2）。Allan 标准差就是Allan 方差的平方根，或者 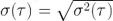。我们可以针对一系列观测时间 τ 评估该表达式，以深入了解数据在不同时间尺度上的自相似性（即稳定性）。

 

 

从式（1）可以看出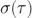， 的维度与 y 相等。我们将该值解释为间隔 τ 秒的 y 测量值在两个 τ 秒之间的预期均方根差。

 

 

例如，假定一个时钟振荡频率在 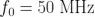。如果其分数频率差的 Allan 方差 - Y，表达式为：

 

 

 

 

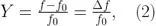
在10秒观测时间 （τ = 10 s）上为 1.23x10-10  ，然后我们可以预计 Y 其两个随机选择并连续的 10 秒观测时间测量值相差为 1.23x10-10 RMS。在给定的部分频率差定义下，这等于一个预期的绝对频率差 。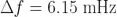

 

 

现在我们思考长度为 M 的真实有限数据集的情况，以周期  进行采样（图 3）。我们不能在一个采集系统内自由地选择总时间 τ，所以我们将时长 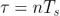划分成 K 个数据分段，这里 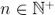。Allan 方差可以粗略地近似为：

 

 

 

 

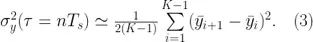
这里在 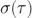的不确定度是 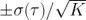。测量不确定度的完整处理方法不在本文讨论范围之内，因此请参阅参考文献 [4] 了解更多详细信息。为了改善结果的可靠性并且比较高效地使用数据值，我们可以将数据划分为重叠段（图 4），这得到了 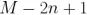对连续的分段，与之前的 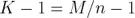正相反。这样重叠的 Allan 方差可以表示为：

 

 

 

 

 

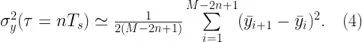
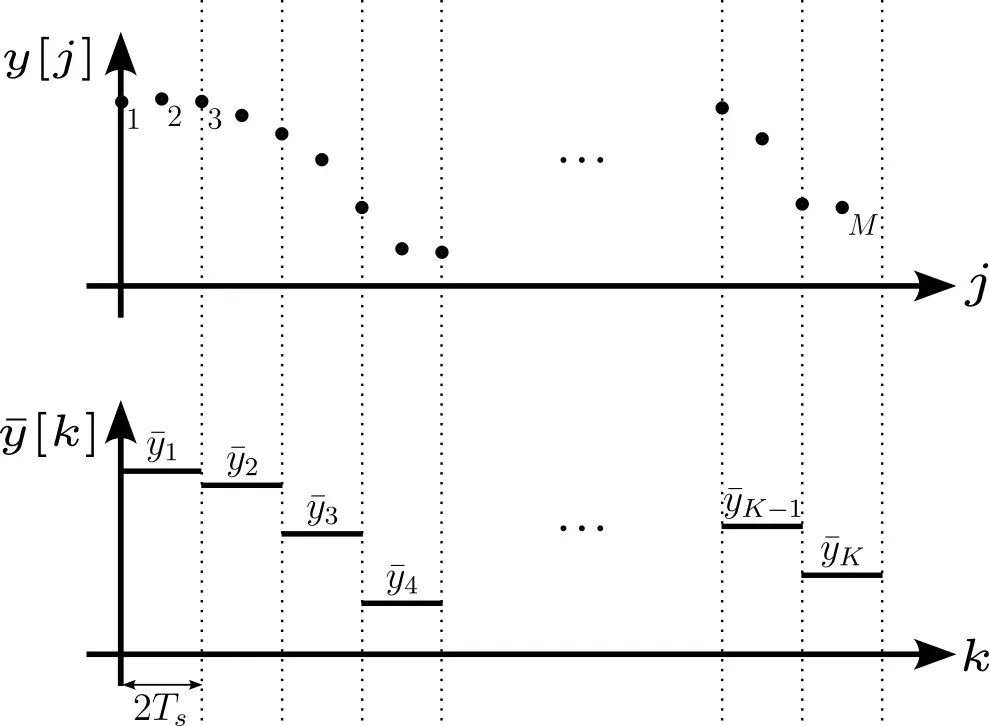
图 3：在真实的采样系统里，数据量是有限的，同时 τ 被限制在几倍采样周期内 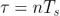（这里 n = 2）

通过积分获得 Allan 方差

 

在许多常见的测量场景下存在一个变量 x，其属性如下式所示：

 

 

 

 

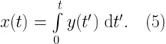
例如在时钟稳定度测量中，时间偏差 X 是部分频率差 Y 的积分，例如在陀螺仪系统中，被测角度， θ 即旋转速度 Ω 的积分。

 

 

 

 

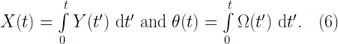
我们可以通过式（5）的积分来计算 x，即使它不和某个被测物理量相对应。

 

 

 

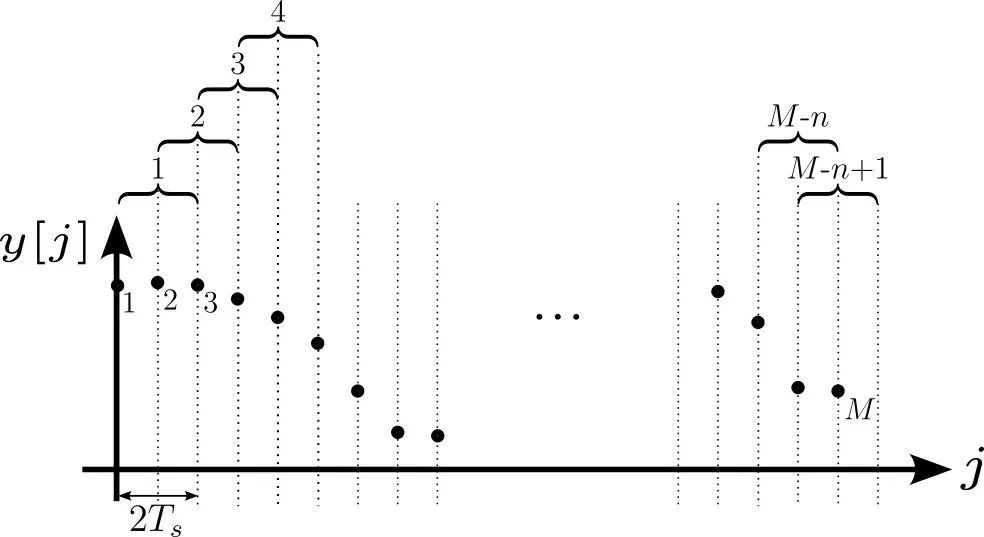
图 4：为了最优化使用这些数据值，分段会重叠。这创建了额外的连续观测时间对，所以增加了等式（3）中可能的被加数数量。在这个 n = 2 的案例中，受制于非重叠的分段，我们可以执行减法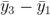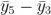：， 等等。现在我们还有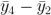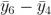：， 等等。尽管样本并不完全独立，但我们结果的可信度仍然有所提高。

 

 

在这种情况下

 

 

 

 

 

 

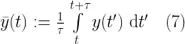
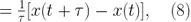
或者用离散函数表示，

 

 

 

 

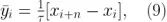
这样等式（4）就变成

 

 

 

 

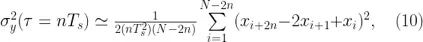
这里 N = M + 1 是 x 的长度。为了理清这一点，我们可以考虑 y 通过 x 的数值导数（差）来构造，因此 M = N − 1。

 

 

这似乎像一个很抽象的简化定义，当出于计算效率的原因，等式（10）提供了 Allan 方差最普遍的方程式。注意这里，x 测量值提供的是 y 的 Allan 方差，而非 x。

 

 

绘制 Allan 方差图

 

Allan 方差通常针对多个平均时间进行运算，并且以 log - log 刻度绘图（图 5）。这样的图形有助于确定给定测量值的最佳平均时间。注意我们不会总是推荐使用较长的平均时间，特别是存在低频漂移的情况下。

 

 

另外，常见的噪声源一般以幂定律描述，它在 Allan 标准差图上呈现已知的斜率。例如，白噪声会随着平均时间的平方根而减少。所以我们能够预期白噪声的斜率为 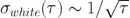，情况也确实如此。更普遍的是，如果特定噪声源在功率谱密度 S 的斜率是 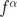，则 Allan 标准差的斜率即 。

 

 

 

 

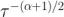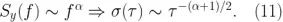
这一事实使人们能够轻松确定哪个噪声源在不同的平均时间内占主导地位，建立噪声预度以确定系统性能是否得到充分理解，或量化每个误差源的分布（图 6）。

 

 

表 1 罗列了在研究时钟和陀螺仪时常见噪声源的斜率

 

 

表 1：针对选定应用中的不同噪声源的斜率幂指数 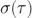（即 β 是 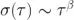）[3, 5]。FM：频率调制方式，PM：相位调制方式。

 

 

 

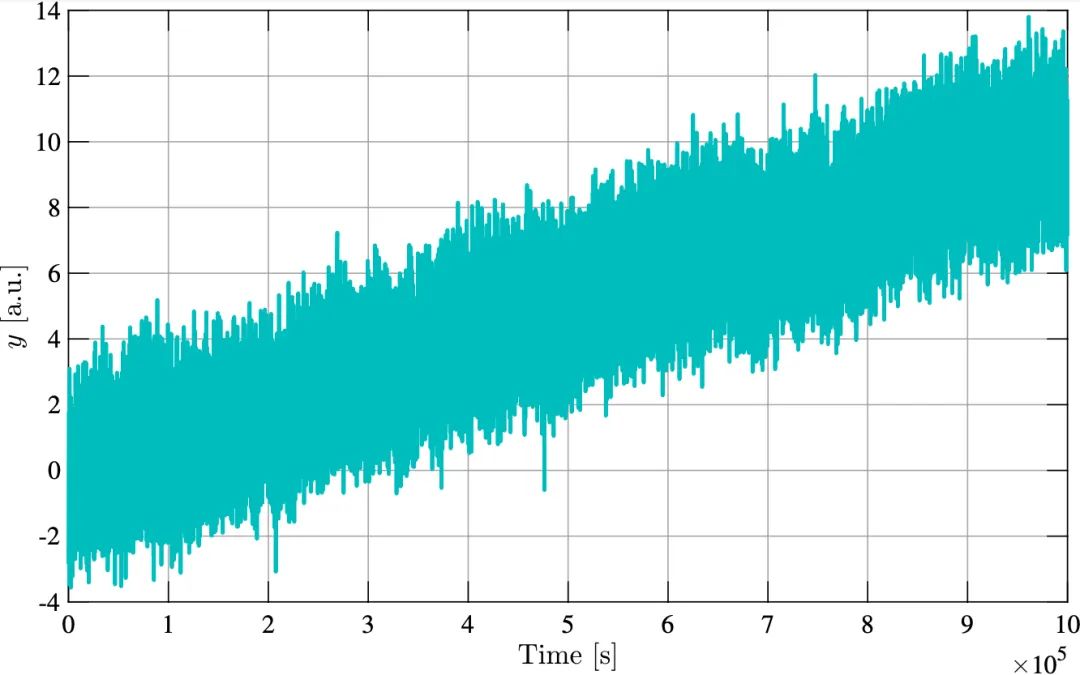
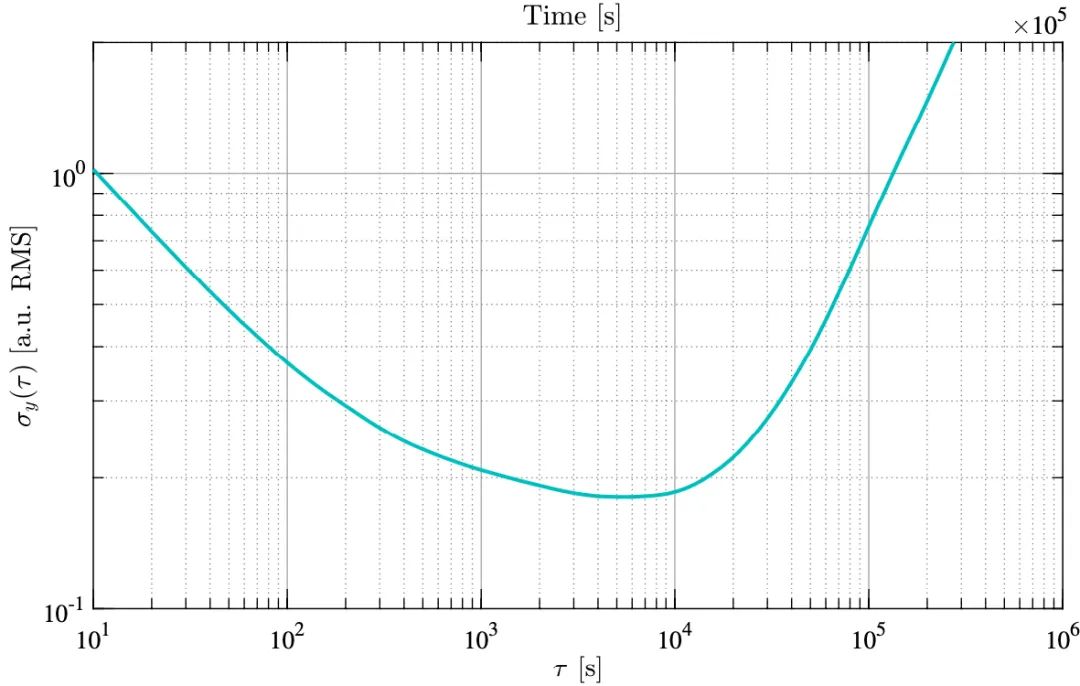
图 5：时间序列（上轴）样例，同时它相对应的 Allan 标准差图（下轴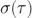）。 针对多个平均时间 τ 进行评估，结果以 log - log 刻度显示。

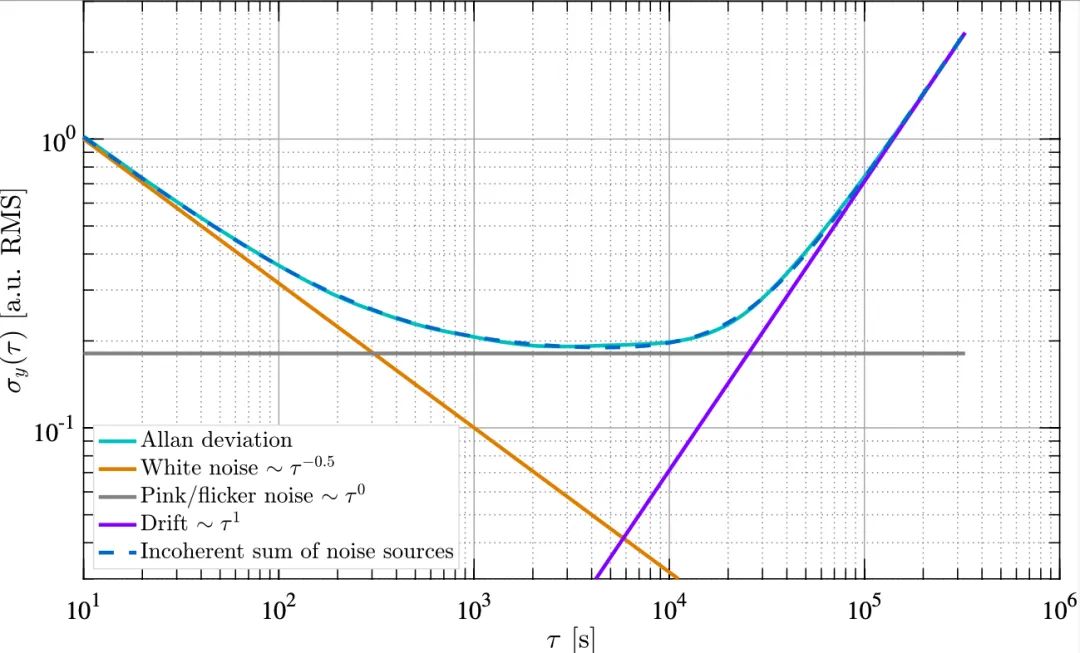
图 6：幂定律噪声源在 Allan 标准差图上显示为已知的斜率，让我们可以容易地对系统噪声建模。总的噪声定义为不相干的独立噪声分布总和，即 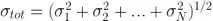。在这种情况下，稳定性随着平均时间的推移而提高（因为白噪声的影响减少），直到粉红/闪烁噪声成为主导。在较长的时间尺度上，稳定性受到数据线性漂移的限制（参见图 5，上轴）。当平均时间约为 5000 秒时，测量结果最为稳定。

 

 

如何在Moku配置Allan 方差测量

下方视频演示如何在Moku配置Allan 方差测量。

 

功率谱密度 vs Allan 方差

 

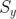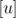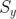就像我们前面提到的，有许多的工具可用于描述系统稳定性。虽然 Allan 方差是稳定性在时域上的计量，那功率谱密度（PSD）， 就是频域上的对应项。如果 y 的单位是 ，则 的单位是 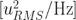。当然在 Allan 方差中所包含的信息 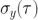只是 PSD 中包含信息的替代表示，并且存在一个很接近的转换形式（参考 [6] 中的附录I）。注意这个只可以是从 PSD 向 Allan 方差的转换，相反则不行。转换方程如下：

 

 

 

 

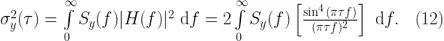
这里 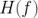是时域采样函数的传递函数。

 

 

在这个情况下，我们需要注意一个有用的表达式：

 

 

 

 

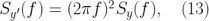
这里 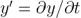。我们可以以此为例，根据 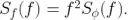转换 相位(φ) 噪声的 PSD 为频率 (f) 噪声之一。

 

 

结果

 

我们在本文中已经介绍了 Allan 方差，展示如何计算并解释分析。最初是在振荡器稳定性的背景下开发的，目前仍是最常用的统计方法。不过 ，我们需要强调它适用于任何时间序列并且在广泛的领域中大有用处。

 

 

Allan 方差有助于确定特定测量下的理想观测时间并识别主要的噪声源。还可以将功率谱密度转换为阿伦方差。

 

 

Allan 方差是一种非常有用的统计工具，也是 Moku 相位表上可用于数据后续处理的众多此类工具之一。其性能以及相位表的微弧度级精度和 Moku:app 的直观用户界面，使 Moku 成为在表征振荡器系统稳定性的应用中卓越的设备。

 

 

除 Allan 方差之外

 

正如标准差存在局限性一样，Allan 标准差也不是在所有情况下都是理想的统计方法。为了考虑完整，这里简要讨论了 Allan 标准差的两种常用导数，它们在某些情况下提供了改善的性能。

 

 

修正 Allan 标准差

 

我们在上面注意到了在 Allan 标准差图上（图 6）基于梯度轨迹识别噪声源的可能性。然而多个噪声源会存在同一个斜率。特别是振荡器白噪声相位调制（WPM）和闪烁噪声相位调制（FPM）会同时产生一个 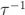斜率（如表 1）。然而，WPM 对测量带宽非常灵敏，FPM 则不然。通过在 n 个相邻测量之间部署额外的平均方法，这里 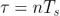，这样修正后的 Allan 标准差，产生随 τ 线性变窄的有效带宽，同时能够区分这些噪声源 [7]。

 

 

修正的 Allan 标准差可以表示为：

 

 

 

 

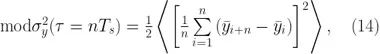
或者更实际一点，

 

 

 

 

 

 

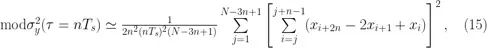
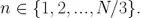
时间偏差

 

基于修正的 Allan 标准差更进一步的计量是时间偏差，或者时间 Allan 标准差 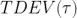，可以表示为：

 

 

 

 

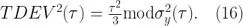
注意这不过是修正 Allan 方差的另一个版本（所有在 log - log 图上的斜率通过 τ 的一次幂减少）。选择归一化因数使得当 n = 1 时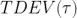， 与白相位调制（PWM）噪声保持一致。

 

 

TDEV 也经常用 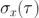表示，明确了它是描述 x 稳定性（而不是 y）的事实。这是由于附加因子 τ 造成的。

 

 

顾名思义，这种测量在表征时序分布信号非常有用，它用于描述时钟的相位变化来作为平均时间的函数。