IIR/FIR系统对连续采集数据的滤波处理和模拟仿真

在之前我们的博文中，所提到的数据的滤波处理和仿真分析，其实都是围着一段固定长度的模拟数据展开的，除了知道滤波器的幅频、相频响应特性之外，也直观地看到了滤波的效果会是怎么样的。实际应用会怎么样？需要怎么处理？

假设需要对音频，视频，或者储存的大量数据等进行处理时，期待全部读取然后一次处理显然是不合适，也没有必要，而且资源和实时性都无法满足。而分段处理，需要的资源少是一方面，并行和分布处理难道不考虑一下？

那分段处理，能否将每段滤波之后获取的数据直接拼接作为整体滤波后的数据呢？然而分段处理需要考虑有其特殊性。

就信号处理而言，FIR系统和IIR系统的处理方式各有特点。

IIR系统的连续采集滤波

IIR系统的输出不仅依赖于当前和过去的激励输入，而且还依赖于系统过去的输出（反馈）。IIR系统的特性是有无限长的冲击响应，理论上即使停止了前馈输入，它还有系统过去的输出继续作为反馈输入，从而维持输出。如果一定要卷积IIR系统，通常要做适当的截断和近似处理，才可以让IIR滤波的效果在有限的计算资源使用卷积。不过虽然理论可卷，实际多用时域递推的方式。

IIR系统的递推计算，之前我们提供的示例C++滤波器代码中，是为了演示，一次性批发处理多个数据，实际处理是可以根据应用来调整每次输入数据的长度。无论是分段处理还是单个输出，如果保留了过去的输入和输出状态，是可以持续进行处理的。下面是每次输入一个信号x(n)，然后生成/读取一个输出y(n)，一定要正确保留每次的输出和输入。

下面是一个简单IIR单输入滤波的示例，参数没有哈。当然，把这个转换为FIR的滤波处理也是很自然的事情。

 

#define N 3          // 设置滤波器的阶数


double a[N] = {...}; // 这是滤波器的反馈系数
double b[N] = {...}; // 这是滤波器的前馈系数
double x[N] = {0};   // 这是输入的缓冲数组
double y[N] = {0};   // 这是输出的缓冲数组


double iir_filter(double input)
{
    int i;
    // 更新输入缓冲数组，循环更替
    for (i = N - 1; i > 0; --i)
    {
        x[i] = x[i - 1];
    }
    x[0] = input;
    // 计算当前的输出
    double output = 0;
    for (i = 0; i < N; ++i)
    {
        output += b[i] * x[i] - a[i] * y[i];
    }
    // 更新输出缓冲数组
    for (i = N - 1; i > 0; --i)
    {
        y[i] = y[i - 1];
    }
    y[0] = output;
    return output;
}

 

如果IIR系统长数据分段没有保存过去的状态，我们可以得到下图。

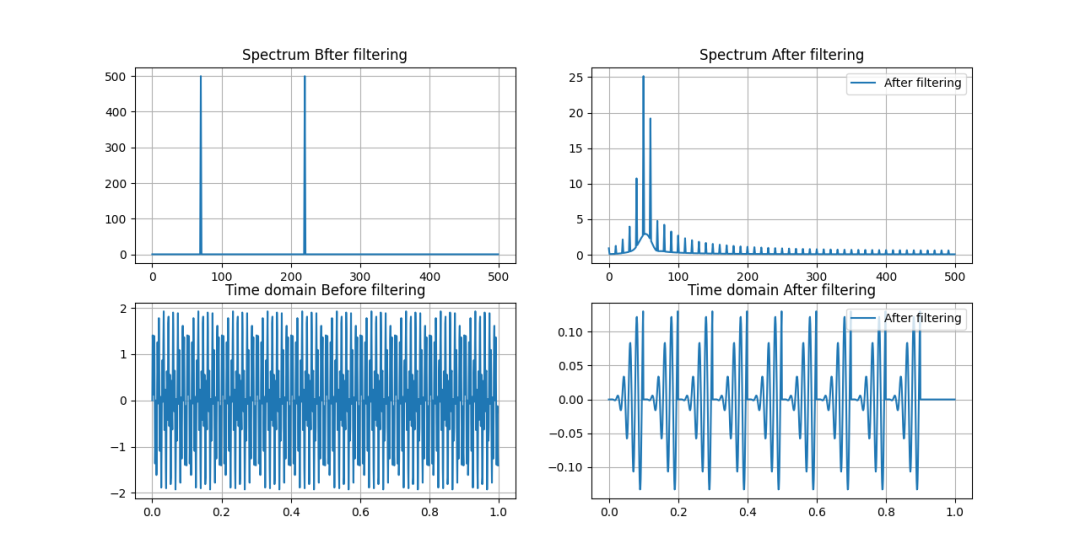
IIR分段滤波没有保留过去的状态

过滤没有处理好，还生成了额外的干扰信号。总之，IIR系统中忘记历史，就会有惩戒啊。

如果IIR系统长数据分段保存过去的状态，我们可以得到下图：

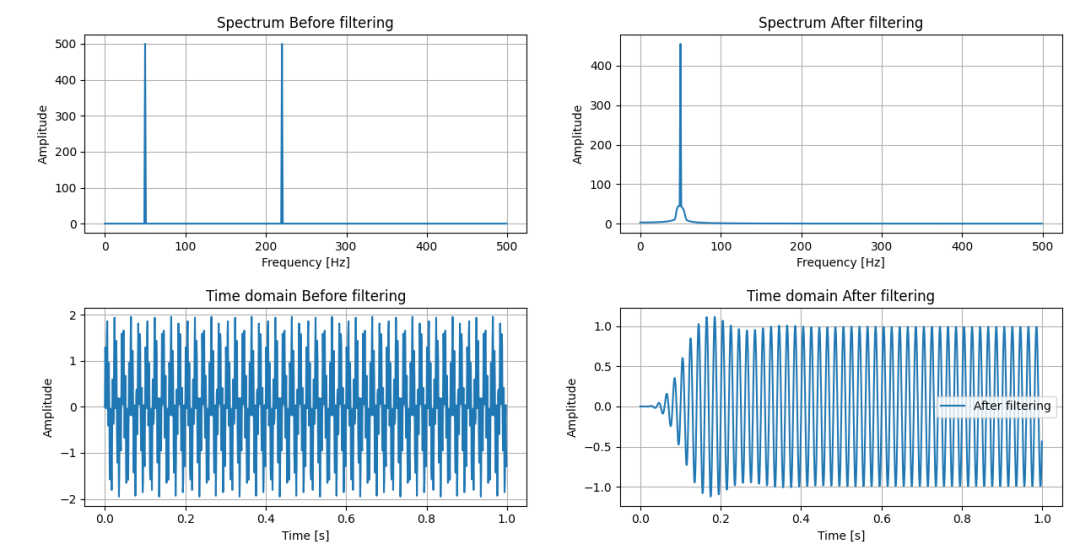
IIR分段滤波有过去的状态

前面两组图相比，差异是不是一目了然？下面是IIR系统每次分段考虑了过去状态的Python模拟代码。

 

# IIR 系统分段处理：过去状态的处理
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from numpy.fft import fft, fftfreq


# 创建模拟信号
# 采样频率
Fs = 1000
nyq = 0.5 * Fs


# 设定阻带频率
low = 45.0
high = 55.0


# 按照通带和阻带频率的顺序来设计滤波器
lowcut = low / nyq
highcut = high / nyq


# 使用iirdesign设计滤波器
b, a = signal.iirdesign([lowcut, highcut], [lowcut - 0.05, highcut + 0.05], gpass=1, gstop=60, ftype='butter', output='ba')


T = 1.0 / Fs # 采样时间间隔
t = np.arange(0, 1, T) # 创建时间轴
x = np.sin(2 * np.pi * 50 * t) + 1 * np.sin(2 * np.pi * 220 * t) # 50Hz和120Hz信号叠加
# 创建一个与x长度相同的用于保存滤波后结果的数组
y = np.zeros_like(x)


# 分段进行滤波
win_size = 100 # 窗口大小
zi = signal.lfilter_zi(b, a) * x[0] # 计算初始状态
for i in range(win_size, len(x)+1, win_size):
    y[i-win_size:i], zi = signal.lfilter(b, a, x[i-win_size:i], zi=zi)


# 计算输入信号和输出信号的频谱
frequencies = fftfreq(len(t), 1/Fs)
x_spectrum = np.abs(fft(x))
y_spectrum = np.abs(fft(y))


# 绘制幅频响应图
w, h = signal.freqz(b, a)
plt.figure()
plt.plot(w/(2*np.pi), abs(h))
plt.title('Frequency response')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Gain')
plt.grid()


# 绘制频谱图
plt.figure(figsize=(9, 6))
plt.subplot(221)
plt.title('Spectrum Before filtering')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Amplitude')
plt.grid()
plt.plot(frequencies[:Fs//2], x_spectrum[:Fs//2], label='Before filtering')
plt.subplot(222)
plt.plot(frequencies[:Fs//2], y_spectrum[:Fs//2], label='After filtering')
plt.title('Spectrum After filtering')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Amplitude')
plt.grid()


# 绘制模拟信号和滤波后的信号
plt.subplot(223)
plt.plot(t, x, label='Before filtering')
plt.title('Time domain Before filtering')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.grid()
plt.subplot(224)
plt.plot(t, y, label='After filtering')
plt.title('Time domain After filtering')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.grid()
plt.tight_layout()
plt.legend()


plt.show()

 

FIR系统的连续采集滤波

和IIR系统相比，FIR系统的输出则仅仅依靠当前和过去的输入。但是，要实现相同的滤波效果（不考虑相位线性），FIR往往要更高的阶数才可以完成。阶数越高，意味着越多的资源和越长的系统延迟。

我们知道，FIR滤波器中的每个系数b(n)，都对应于系统的单位冲击响应h(n)。所以，对于FIR滤波器，那我们就可以通过但不限于卷积的方式来处理信号。这里我们围绕卷积的方式来讨论FIR滤波器处理数据分段滤波的两种方法：

重叠保留(Overlap-Save)

重叠相加(Overlap-Add)

下面两个等式分别是卷积和FIR滤波处理。

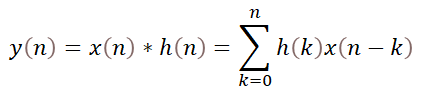
    （1）

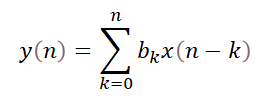
        （2）

如果把b[k]看作h(k)，则水到渠成，FIR滤波器的处理过程就是一个卷积运算。变成卷积后的另外的好处就是，我们可以利用FFT/IFFT来进行某些大型数据的加速运算——时域的卷积等同于频域的乘积。对于小到中等大小的数组序列，一般也就用时域的卷积了。

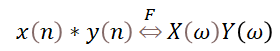
但是卷积从现象上看，当我们参与卷积的FIR滤波器长度为M，被卷积的数据序列长度为L，那么，每次卷积的结果的数据序列N长度会是：

N = M + L -1

当你面对每次多出原先数据序列长度L的结果N时？如何取舍？

如果滤波器是从全0的状态开始的，滤波器需要一定的"预热"时间才能达到稳定的工作状态。滤波器的"预热"过程就是滤波器读取前N个样本的过程。因此，你会看到滤波后的数据最开始部分是从0开始，然后逐渐看到正常的输出波形。

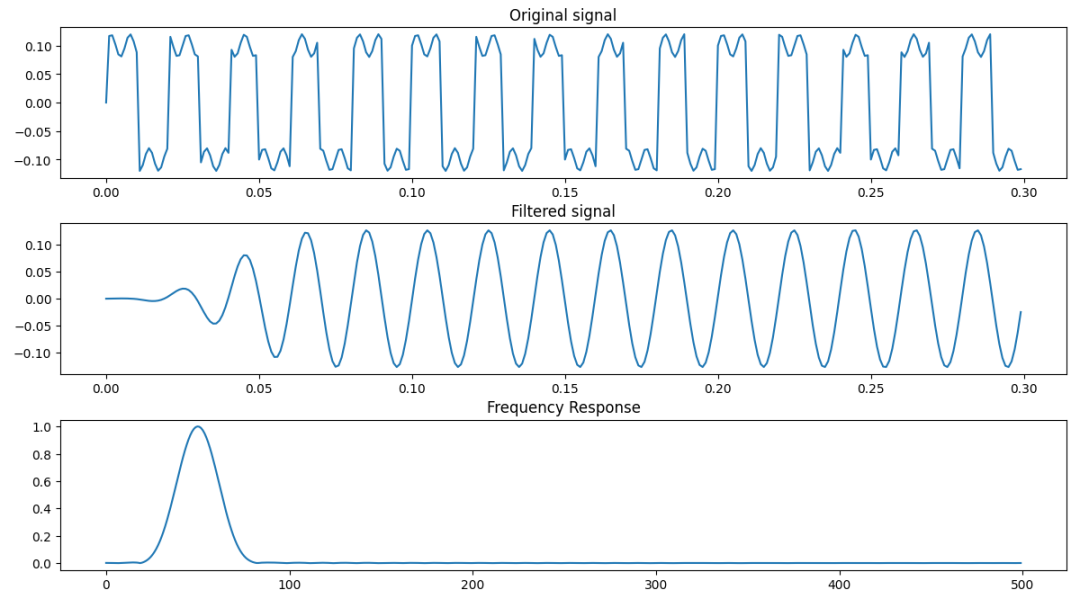
另外，我们示例的滤波器是加窗处理的，而且模拟信号频率比较单一，相距也较远，否则，处理不好的滤波结果会让人感觉出乎意外。因为每次截取一段数据，相对于给采集的数据加了一个矩形窗，而我们在设计滤波器时，是需要对这个矩形窗进行额外加窗处理的。矩形窗对于波形而言存在着频谱泄漏和主瓣宽度等问题，对数据的处理有时候会比较麻烦。——注意，要跑题了吧？

我们看模拟结果。下图为待滤波处理的模拟信号。500Hz+1400Hz。

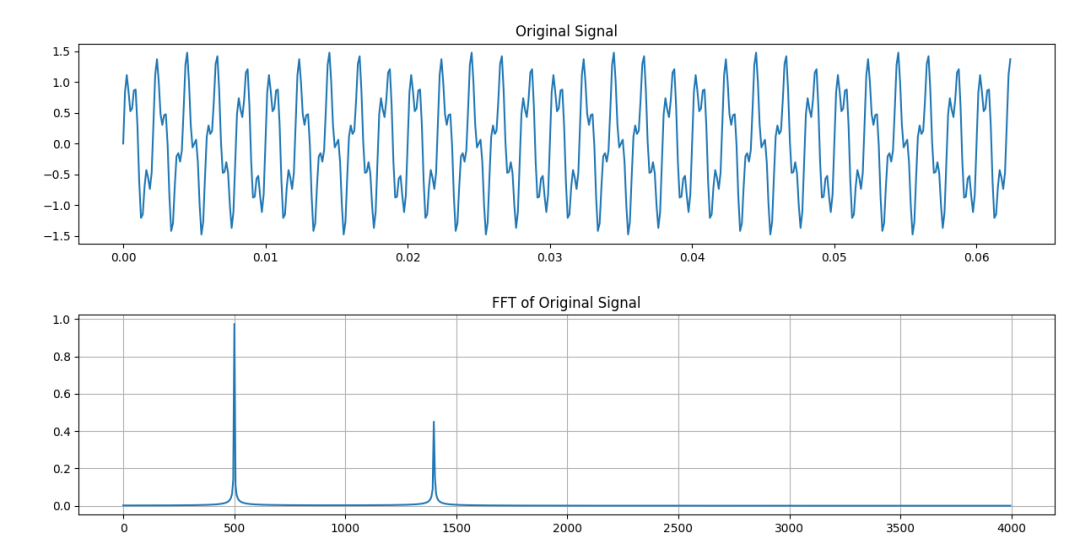
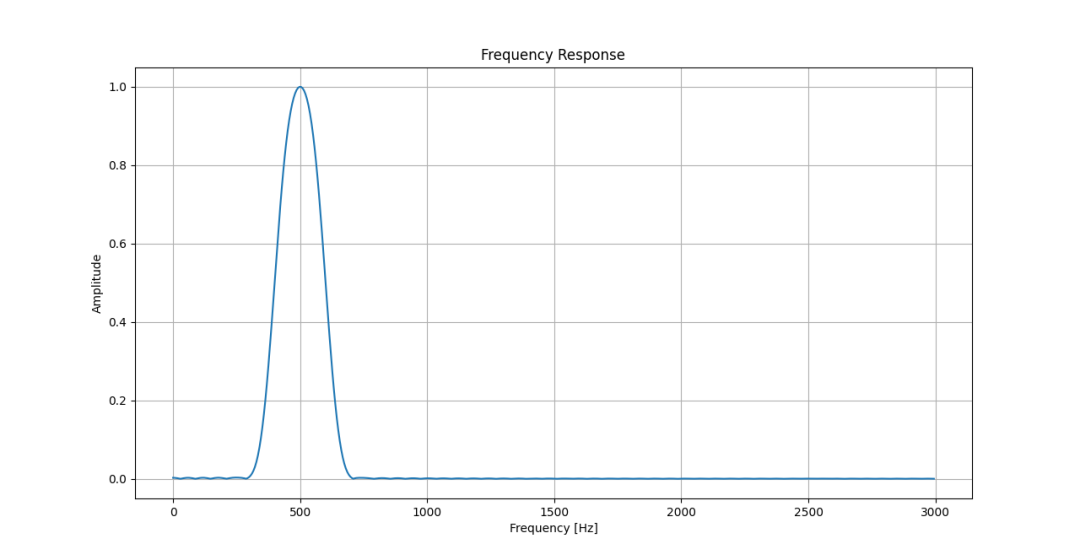
下图为矩形窗滤波器的幅频响应——知道为什么我要选1400Hz作为被滤掉的信号了吧？

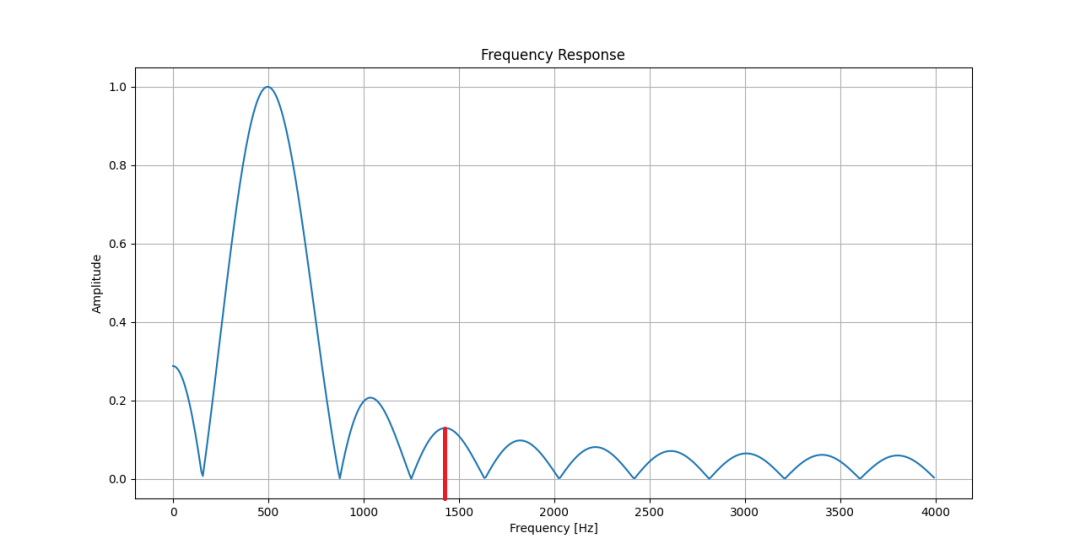
矩形窗选频滤波器幅频特性

这个例子仅仅是为了说明矩形窗的影响。下面是矩形窗滤波器的结果，500Hz+1400Hz的信号经过滤波之后的输出。——跑题十万八千里是为了一扇窗？

（忽略此图）

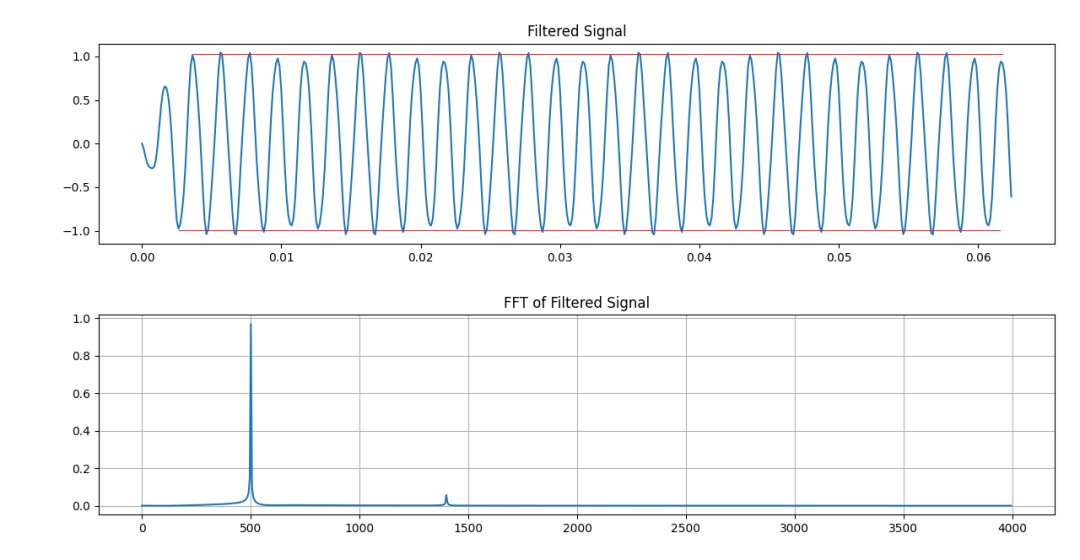
矩形窗滤波器处理结果

而加汉明窗的滤波结果在试验设定条件下则要好一些，同样留意1400Hz处。如下图。

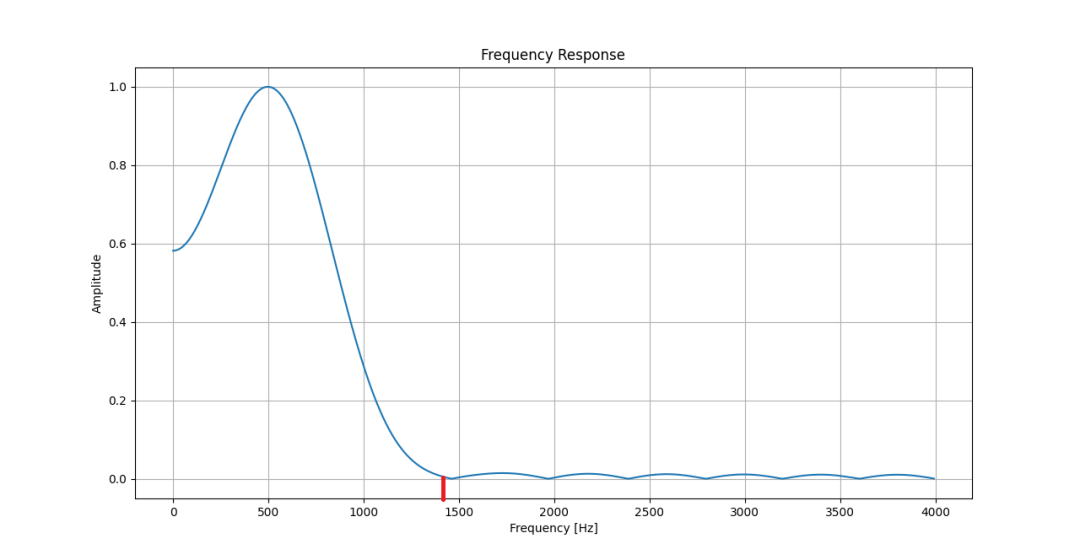
汉明窗滤波器的幅频特性

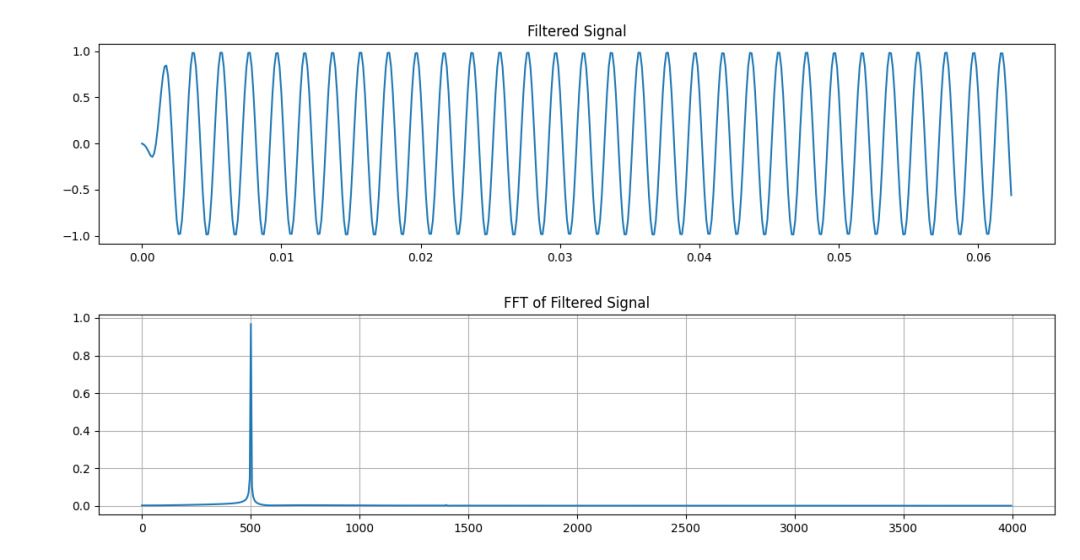
加汉明窗的滤波结果

以上处理为了差异效果，对于滤波器长度、一次处理数据长度，两个信号频率的距离都是作了特别的处理。谁说实际应用中不会碰到呢？

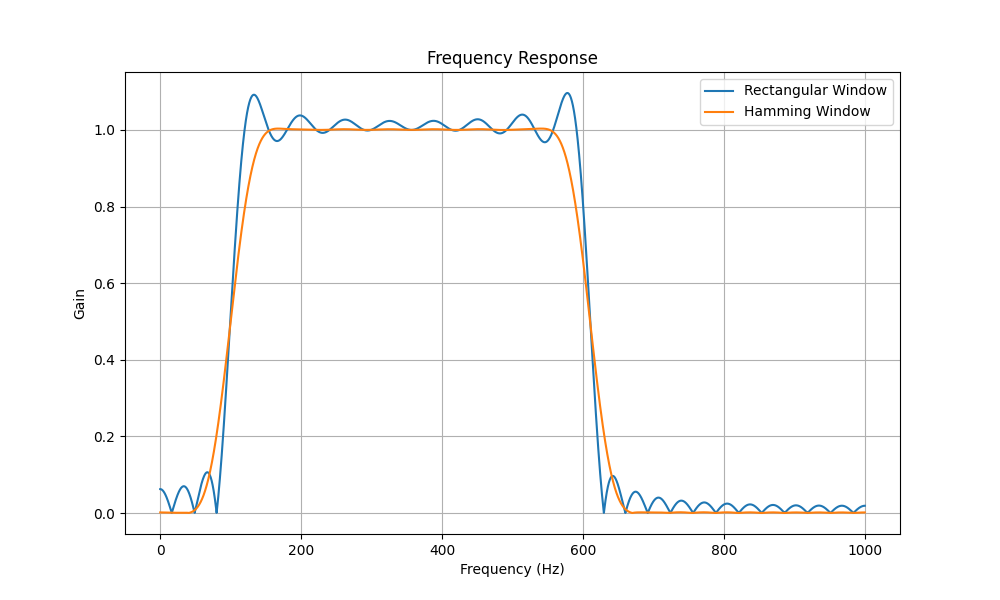
带通滤波器不同的加窗幅频特性

以下内容，都默认已经加窗。

我们再次回到FIR系统使用重叠保留(Overlap-Save)和重叠相加(Overlap-Add)的方式进行分段处理这个话题。

如果FIR系统在频域通过DFT/IDFT并采用重叠保留的方式，那应该是按照下图的方式进行的。

对于FIR滤波器长度为M，数据段长度为L时，流程大致是：在第一个数据段加M-1个0，其余的数据段都是加上前一段的最后M-1个数据；然后进行DFT/IDFT处理得到长度为(L+M-1)的y(n)序列，然后去掉前面M-1个无效值，保留后面的L个。

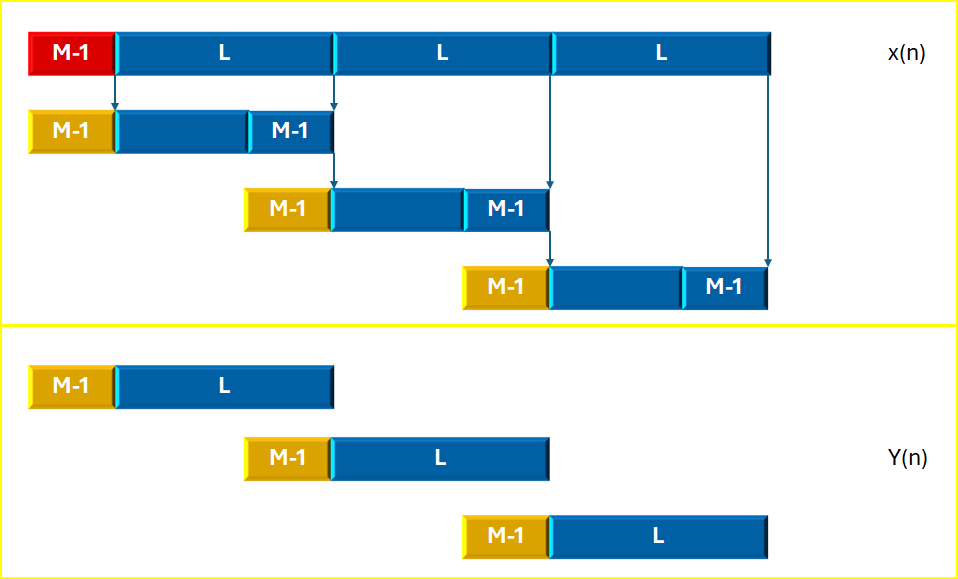
频域中FIR系统的重叠保留法示意图

在时域我们也想照猫画虎的。然而，对于FIR滤波器长度为M和信号的长度L进行卷积，其结果的长度将会是M + L - 1。在实际应用中，我们通常关注的部分是两个序列完全重叠的区域，也就是“有效值”。这意味着如果两个参与卷积的长度不一样（一般L>M)，那最后的“有效值”是需要在卷积的结果序列上两头都要掐掉（M-1）个元素。所以实际卷积结果中的有效序列长度是：

[L+M-1-2（M-1)]=L-M+1

在Python中，卷积函数np.convolve(data_segment, b, mode)对指定长度的数据data_segment（长度L），和FIR滤波器系数序列b（长度M）进行卷积，而输出的结果序列则分为以下三种：

full：        结果长度=M+L-1

same:        结果长度=max(M,L)

valid:        结果长度=max(M,L)-min(M,L)+1=L-(M-1)

为了测试时域中的重叠保留处理方式，小编选了上面卷积函数的valid模式。

在重叠保留方式下，每次参与卷积的数据长度不是L，而是每个数据L起始处，都额外添加了（M-1）长的0（第一个）或者前一段数据的最后（M-1）个数据，再与长度为M的滤波器卷积。这种情况下，参与卷积的数据长度和生成的卷积结果长度是有变化的。

L和M长序列进行卷积得到的full长度为：M+L-1；

那如果将L+(M-1)和M长的序列进行卷积，得到的full长度为：L+(M-1)+M-1=L+2(M-1)；

根据步骤2，我们把得到的full长度的结果两边减去(M-1)就可以得到一个长度为L的有效卷积序列值。

所以这个操作和频域中DFT、IDFT之后得到的保留方式有差异，因为时域中卷积之后的分段结果数据的长度会由L+M-1变为L+2(M-1)，最终取卷积有效值段的长度就等于[L+2(M-1)-2(M-1)]=L。

下面提供模拟仿真。输出图和Python模拟代码。（没有画时域卷积中FIR系统的数据长度示意图，无他，偷懒。）

在500Hz信号中混有1400Hz和2400Hz的干扰。采用分段滤波的方式对FIR滤波器进行卷积处理。我们仍然把它命名为“重叠保留法”。

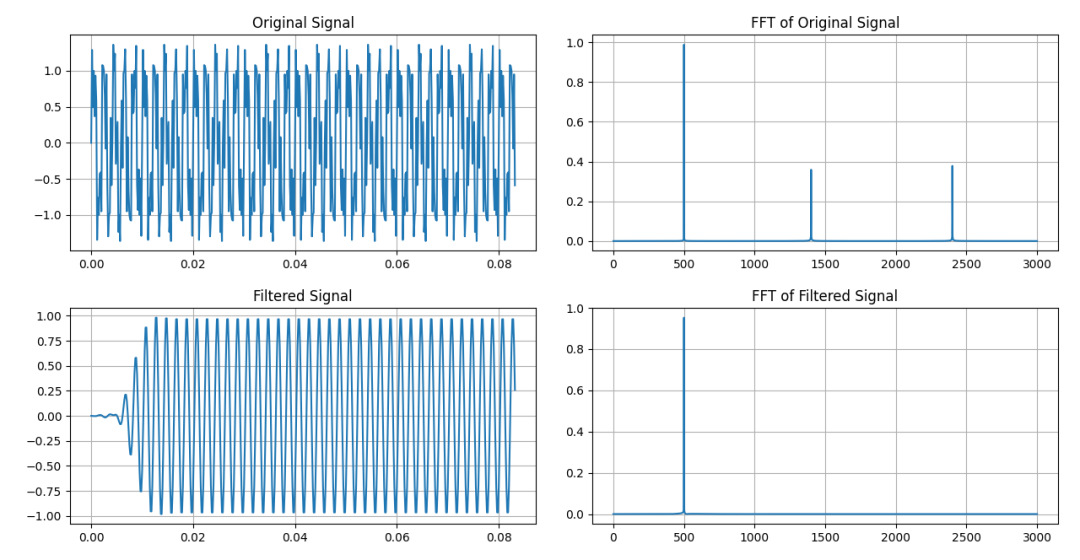
FIR系统时域卷积的重叠保留法

 

# FIR系统时域卷积：重叠保留法
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy.fft import fft,fftfreq


# 设置采样率和数据长度
fs = 6000


# 创建带通滤波器
# Create a bandpass filter
f1 = 400
f2 = 600
filter_len = 100         # FIR滤波器长度
b = signal.firwin(filter_len, [f1, f2], pass_zero=False, fs=fs, window='hamming')  #boxcar 


# 设置数据长度：模拟每次采集同样长度的数据
# segment_len，是按照np.concatenate函数在Valid模式下卷积后有效长度来计算的
seg_filter_len = 512                            # filter output length of each segment data
segment_len = seg_filter_len - filter_len + 1   # 分段数据目标长度 seg_filter_len = segment_len + filter_len - 1
target_length = segment_len * 50                # 总数据长度


# 而新的时间序列的上限
TimeSpace = target_length / fs


# 生成的时间序列为L的整数倍，模拟每次采样的数据的长度
t = np.arange(0, TimeSpace, 1/fs)


# 产生一个含有1.4KHz，2.4KHz和500Hz信号的模拟信号，其中1.4，2.4KHz的信号将被过滤
x = np.sin(2 * np.pi * 500 * t) + 0.5 * np.sin(2 * np.pi * 1400 * t) + 0.5 * np.sin(2 * np.pi * 2400 * t)


# Filter and segment with overlap-save method
# each segment length should be longer than filter's length
y_result = []
segment = None
for i in range(0, target_length, segment_len):
    if i==0:
        # 第一段数据滤波前，前面填充(M-1)个0，再加开始的L个数据参与滤波卷积
        segment = np.concatenate((np.zeros(filter_len-1), x[0:segment_len])) 
    else:
        # 对后续的每个段，包括从上段的末尾取(M-1)个点，再新取L个点，这里M指滤波器长度,L指拟当前新取的数据长度
        segment = np.concatenate((x[i-filter_len+1:i], x[i:i+segment_len]))
    
    # 每个段使用“valid”卷积模式，所以每次卷积后的有效数据长度是:L = L + 2(M-1) - 2(M-1) = segment_len
    conv = np.convolve(segment, b, mode='valid')
    # 与结果进行合并连接
    y_result = np.concatenate((y_result, conv))


# Frequency response of filter
w, h = signal.freqz(b, 1, fs=fs)
plt.figure()
plt.plot(w, abs(h))
plt.title('Frequency Response')     # 频率响应
plt.xlabel('Frequency [Hz]')        # 频率
plt.ylabel('Amplitude')             # 幅度
plt.grid()


# Plot the original signal and its FFT
n = len(x)
freq = fftfreq(n, 1/fs)
y = fft(x)


plt.figure(figsize=(9,6))
plt.subplot(221)
plt.plot(t[:500], x[:500])
plt.title('Original Signal')                # 原始信号
plt.grid()
plt.subplot(222)
plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 频谱规范化输出
plt.title('FFT of Original Signal')         # 原始信号的FFT
plt.grid()


# Plot the filtered signal and its FFT
n = len(y_result)
freq = fftfreq(n, 1/fs)
y = fft(y_result)


plt.subplot(223)
plt.plot(t[:500], y_result[:500])
plt.title('Filtered Signal')                # 滤波后的信号
plt.grid()
plt.subplot(224)
plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 频谱规范化输出
plt.title('FFT of Filtered Signal')         # 滤波后信号的FFT
plt.grid()


plt.tight_layout()
plt.show()

 

大胆假设，小心求证。

以上代码并未实证，纯属模拟，各位有兴趣可以试试。

不过我们安费诺的传感器都是久经沙场，经历过各种工况验证的，感兴趣也可以试试。

内容长了看起来都烦，FIR时域的“重叠相加”卷积处理，下回分解。