梳状滤波器的相关知识

1. 引言

请参考我们前一篇文章《数字滤波器（1）——陷波滤波器》的引言段落。我们还是围绕着下面的两个公式展开。公式中，（式-1）时时域的差分方程；（式-2）时z复频域的系统函数形式。

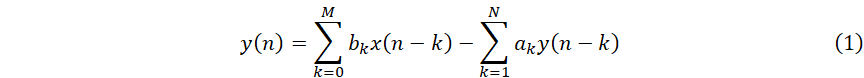
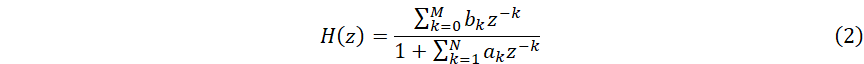
前面提到的陷波滤波器，其功能主要是在相关信号中削弱或者消除特定频率的信号。本文将围绕但不限于梳状滤波器进行展开。其中，梳状滤波器，一方面可以滤除特定的频率（尤其是特定频率的谐波），另一方面也可以在信号中对指定频率及其倍频的信号进行拣选。例如图-1所示的滤除指定谐波成分的梳状滤波器的幅频图。

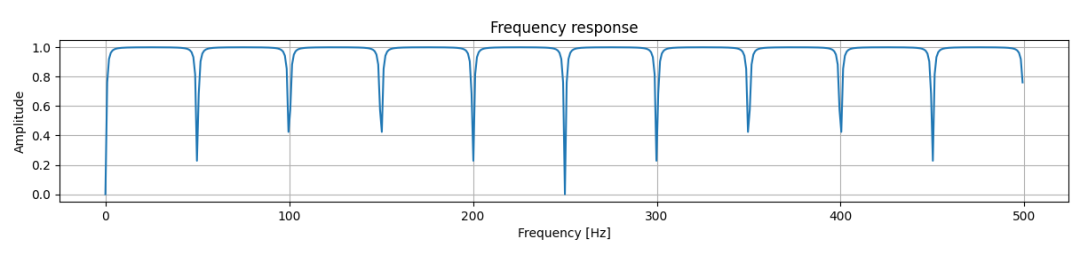
图-1  梳状滤波器幅频响应示意图

2. 关于线性移不变系统和线性相位系统

同样的，关于线性移不变系统的特点，可以查看我们之前的文章《数字滤波器（1）——陷波滤波器》。这里为什么要提出另外一个术语：线性相位，这事关信号传递的保真。

在设计滤波器时，选择具有线性相位(或近似线性相位)的系统非常重要。在许多应用中，如音频处理或图像处理，不仅需要关注滤波器的幅度响应，也需要关注滤波器的相位响应。在通过滤波器的信号的所有频率得到相同的相对延迟（也就是线性相位）可以避免产生相位畸变。相位畸变会在信号中引入不想要的时间延迟，这对于音频信号处理来说尤其重要，因为它可能会改变声音的定位感知。

例如，对于一个音频信号处理应用，如果不同频率的声音延迟不一致，那么声音的定位就会受影响。同样，对于图像处理，如果图像的各个频率部分经过的延迟不同，可能会影响图像的质量，造成图像模糊等。

所以在设计滤波器时，控制相位响应以达到线性或近似线性相位是非常关键的一步。线性相位的滤波器可以确保过滤之后的信号不会出现相位畸变，从而确保原始信号的完整性。 

在信号处理中，"线性时不变系统" 和 "线性相位系统" 是两个具有不同含义的概念。他们的定义和特性如下：

线性时不变系统（Linear Time-Invariant System，或称LTI）：具有线性和时间不变性的系统。线性意味着系统对任何输入信号的响应，等于这个输入信号的线性组合的相应反应的线性组合。时间不变性意味着如果输入信号延后了一段时间，那么输出信号也延后相同的时间。LTI系统的一个重要特性是它们的行为可以通过系统的脉冲响应或者频率响应（即传递函数）完全描述。
 

线性相位系统（Linear Phase System）：系统的频率响应或传递函数在相位上呈线性变化的系统。线性相位系统主要特点是各频率成分通过该系统时具有相同的群延迟，也就是说，所有频率的信号元素都同时到达。这点在很多应用中是很重要的，比如音频信号处理和图像处理，因为它可以防止相位畸变。

一般的，非线性系统是很难实现线性相位的，要说线性相位系统需要基于FIR也不为过。由于信号可以分解成正余弦分量的方式，窥一斑可知全豹，这里不失一般性，我们看一个复指数信号通过一个单位脉冲响应函数h(n)的线性系统会得到什么响应输出。

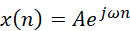
通过卷积我们可以得到响应y(n):

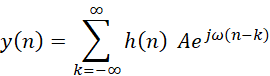
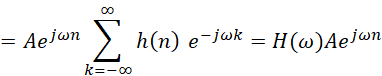
响应输出是在原信号的基础上有幅值|H(ω)|倍数和附加相位arg[H(ω)]=∅(ω)的影响。在很多情况下，同一个系统函数，不同频率的信号输入后，输出时得到的延迟是不相等的。通过设计，我们完全可以控制对输入信号的响应在不同频率时对应的幅值放大倍数。比如下图的一个示例的低通滤波器的幅频响应和相频响应。

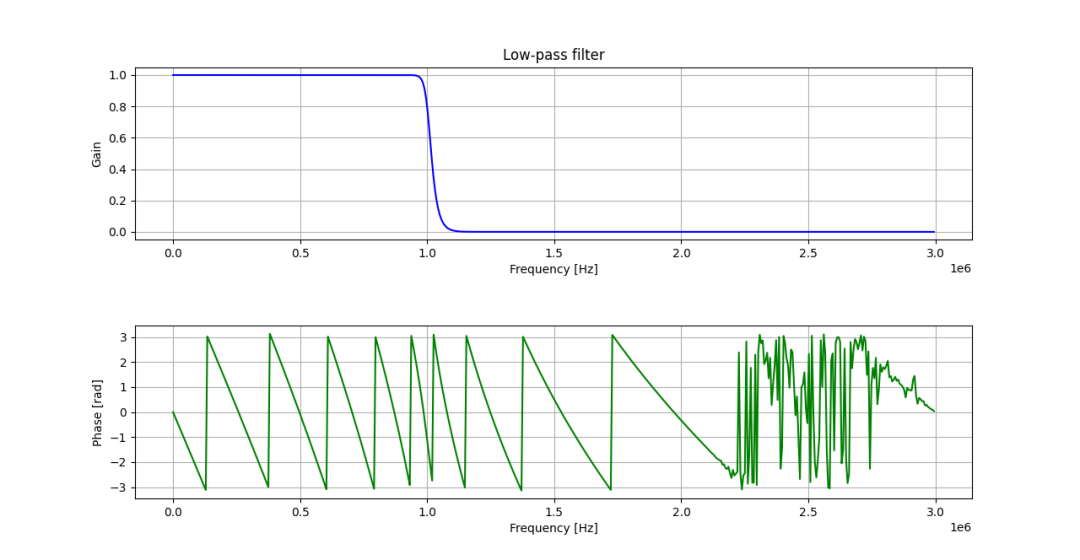
图-2  一般滤波器的幅频响应相频响应示意图

上图所示的系统可以让频率低于1MHz的信号基本保持输入时的响应输出。然而，关于每个频率对应的相位响应就不太确定了。如图-2中在截止频率范围内的相频响应部分。

基本的线性相位要求是群延迟τ为常数：

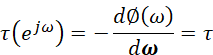
所以这里对应的相位响应：

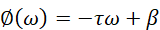
τ和β都为常数。要实现线性相位的特性，IIR是指望不上的，多为FIR系统。通过特别的单位脉冲响应序列的偶对称或者奇对称设计，让频率响应中的相频响应和幅频响应部分可以分离，从而我们在频率响应的结果中看到了一个群延迟τ(e^jω)为所期待的定值结果。

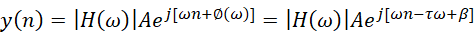
回到时域中后，令:

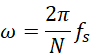
则：

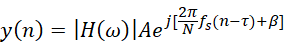
上式中，n和τ都是离散序列中表示时间的。这就意味着输入的所有的有效信号在经过系统之后，都在原信号上增加了一个相同的延迟τ——这就是我们所说的群延迟的来历。

加这一段关于线性相位的补充说明，是要各位留意在实际的滤波器设计过程中，需要根据应用来选择适用的设计，否则反而会引起信号的失真。如下图所示的两种滤波器的群延迟比较，线性相位的基于FIR，非线性相位的基于IIR。(跑题没有？）

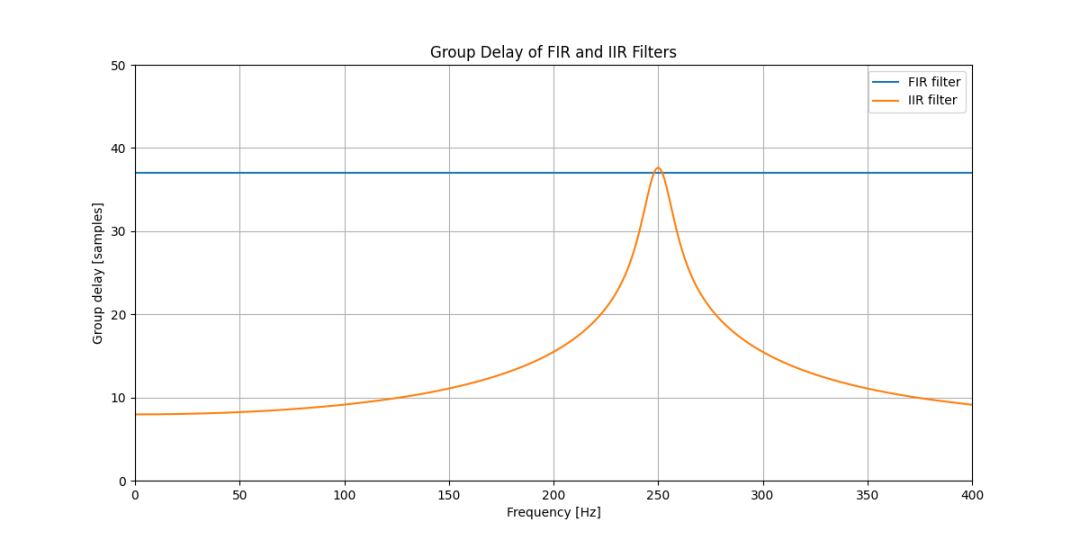
图-3  线性相位和非线性相位的群延迟比较

2. 窄带选频滤波器(Narrowband Selective Filter)

（还在标题范围内不？）在开始梳状滤波器之前，我们再顺便提一下窄带选频滤波器。和陷波滤波器相反，选频滤波是要保留在所选频带内的信号。

窄带选频滤波器属于带通滤波器的一个特例。带通滤波器允许一定范围内的频率通过，而阻止其它频率的信号。如果这个范围非常窄，这样的带通滤波器就可以被称为窄带选频滤波器。它的主要作用是只允许非常特定的频率的信号通过，而其它频率的信号都被阻止。

比如我们打算通过过滤周期方波的形式，用软件的方式过滤谐波，实现基波频率正弦波的输出。

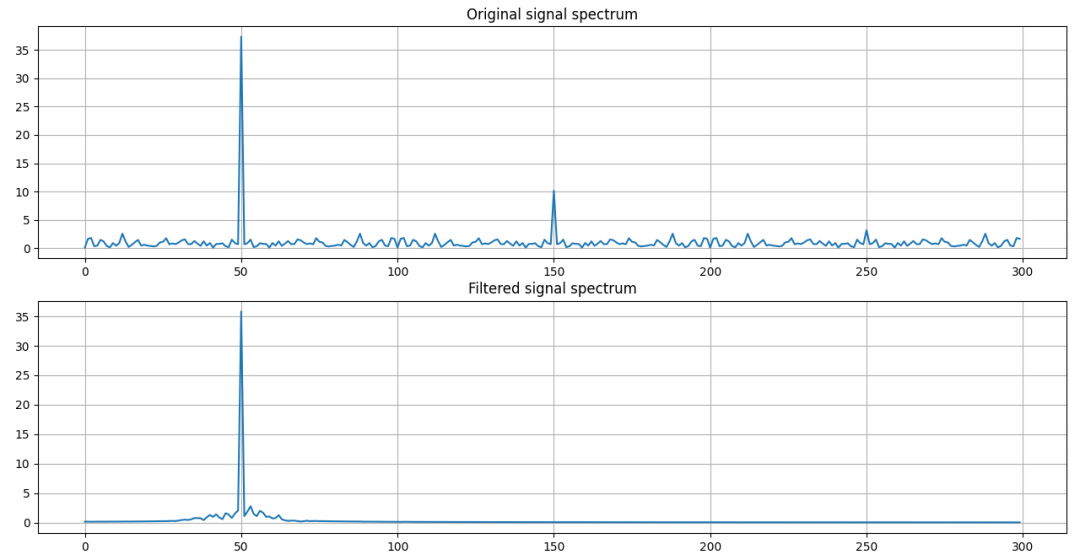
图-4  方波信号滤波前后的频谱图

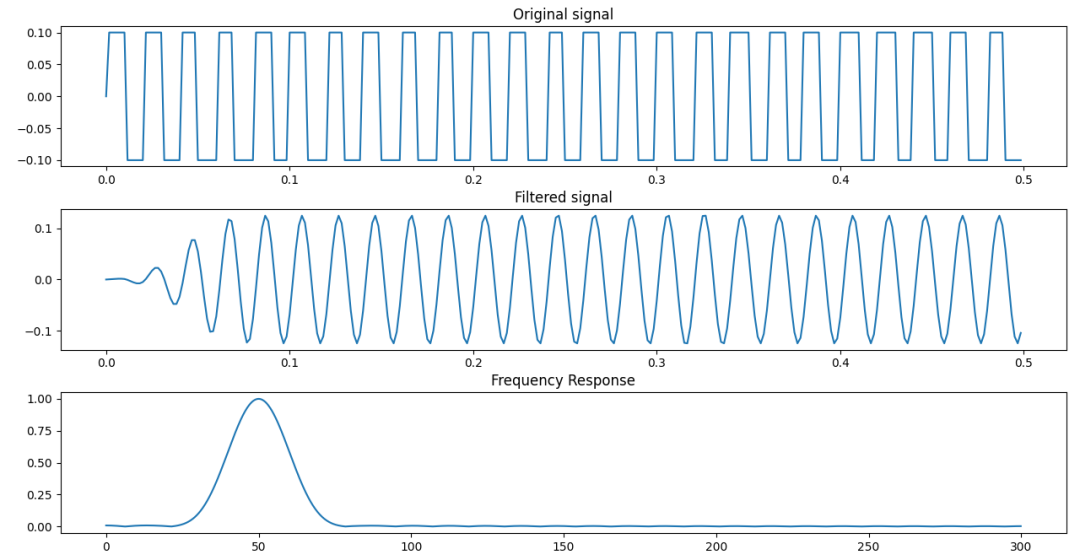
图-5  方波信号滤波前后的波形图和滤波器的幅频响应图

上面的示例中，滤波器的幅频响应并不是设想中的那样在指定频率处加一个非常窄的窗。我们比较一下理想窄带选频滤波器上加不同的窗口函数之后的滤波器幅频响应图。

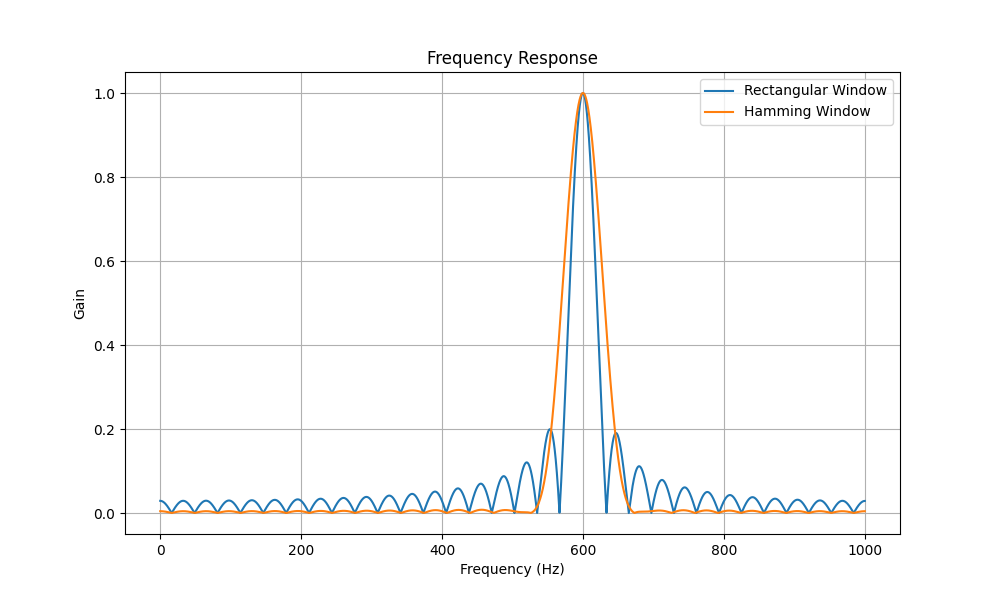
图-6  滤波器加矩形窗和加汉明窗的滤波器幅频响应比较

理想在这里反而是骨感的（那些支棱起的旁瓣），而现实所使用的却略显丰满，不过仍然是折衷的选择。我们必须要在旁瓣大小和过渡区宽度之间做一个权衡选择。

滤波器加汉明窗测试代码如下：

 

from scipy.signal import firwin, freqz
import matplotlib.pyplot as plt
import numpy as np
# 设定采样率、带通频率范围
fs = 2000.0 # 采样频率(Hz)
f1, f2 = 590, 610 # 通带频率范围(Hz)


# 设定滤波器长度
numtaps = 61 # (滤波器系数数量，也就是“抽头”)


# 用firwin设计带通滤波器，先选用矩形窗
taps_rectangular = firwin(numtaps, [f1, f2], pass_zero=False, fs=fs, window='boxcar')


# 再设计使用汉明窗的滤波器
taps_hamming = firwin(numtaps, [f1, f2], pass_zero=False, fs=fs, window='hamming')


# 计算两个滤波器的频率响应
w1, h1 = freqz(taps_rectangular, worN=8000, fs=fs)
w2, h2 = freqz(taps_hamming, worN=8000, fs=fs)


# 创建两个滤波器幅度响应图
plt.figure(figsize=(10,6))
plt.plot(w1, abs(h1), label='Rectangular Window')
plt.plot(w2, abs(h2), label='Hamming Window')
plt.title('Frequency Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Gain')
plt.legend(loc='best')
plt.grid(True)


# 创建两个滤波器相位响应图
plt.figure(figsize=(10,6))
plt.plot(w1, np.angle(h1), label='Rectangular Window')
plt.plot(w2, np.angle(h2), label='Hamming Window')
plt.title('Phase Response')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase (Radians)')
plt.legend(loc='best')
plt.grid(True)


plt.show()

 

3. 梳状滤波器(Comb Filter)

再回到梳状滤波器这个话题。这要是写作文，很担心会走题啊。但是写关于应用方面的东东，其实更多考虑的是面面俱到，因为单独的话题往往会片面。

梳状滤波器，顾名思义，其频率响应曲线像梳子一样，有着很多个频率通道可以穿透或者过滤，中间隔离着独立的频带。梳状滤波器的主要特点是在一定频率范围内有多个通带或者阻带，每个通带/阻带均匀分布。

特性：

梳状滤波器具有良好的二次谐波抑制效果。在应用了梳状滤波器的通信系统中，可以有效避免二次谐波的产生，提高整个系统的信号质量。

梳状滤波器可以避免频率叠加现象的出现，保证了信号在传输过程中的可靠性。

在相同的工作频率和带宽下，梳状滤波器相比于传统滤波器会有更高的功率转换效率。    

应用场合：

无线通信：梳状滤波器是无线通信系统中的关键部件。在射频通信链路中，经常需要对发射机和接收机的信号进行滤波处理，以消除频率上的杂波，提高通信的清晰度和稳定性。

微波设备：梳状滤波器在微波信号的处理和传输中也起着重要的作用。由于微波频段的信号具有很大的带宽，因此，梳状滤波器可以针对特定的频率进行过滤，有效避免信号相互干扰。

射频系统：在射频系统中，梳状滤波器主要用于选择性地阻止某些频率的信号，从而改善射频设备的性能。

数字电视和无线电视接收设备中也经常使用到梳状滤波器。

我们通过模拟信号以及滤波处理后的信号之间进行对比，来了解这种类型滤波器的特点。

如果需要保留基频及其谐波对应的信号，那么就可以用到梳状滤波器了。

模拟信号中有50Hz及其谐波的部分需要保留，保留50Hz和200Hz的有用信号。事先声明，这个滤波器是基于IIR生成的。先看结果，后查代码[2]。

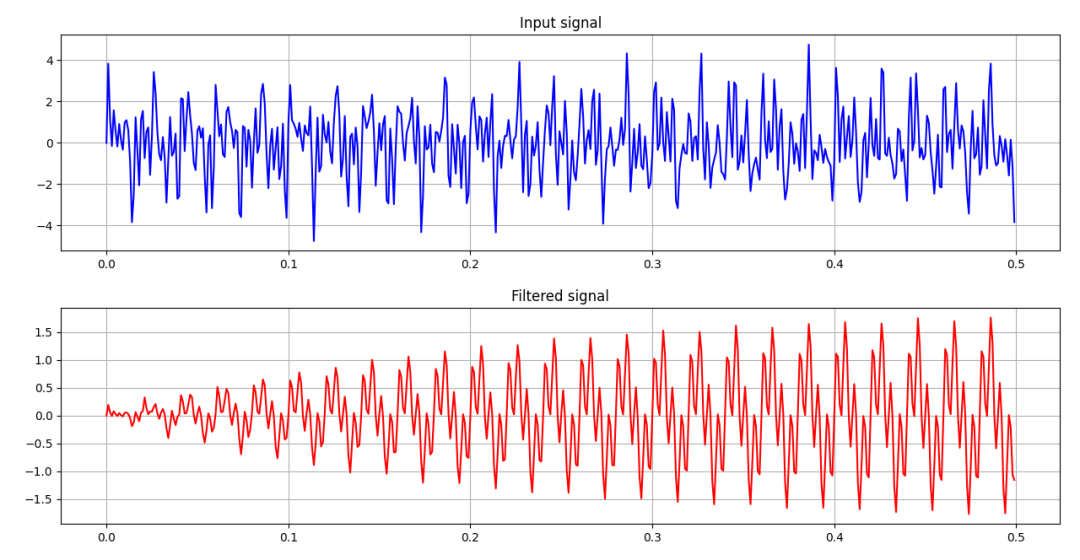
图-7-1   信号滤波前后对比（过滤后仍有50,200Hz频率的信号叠加）

为了更好地感觉梳状选频滤波的效果，我们留单个频率的效果看看。

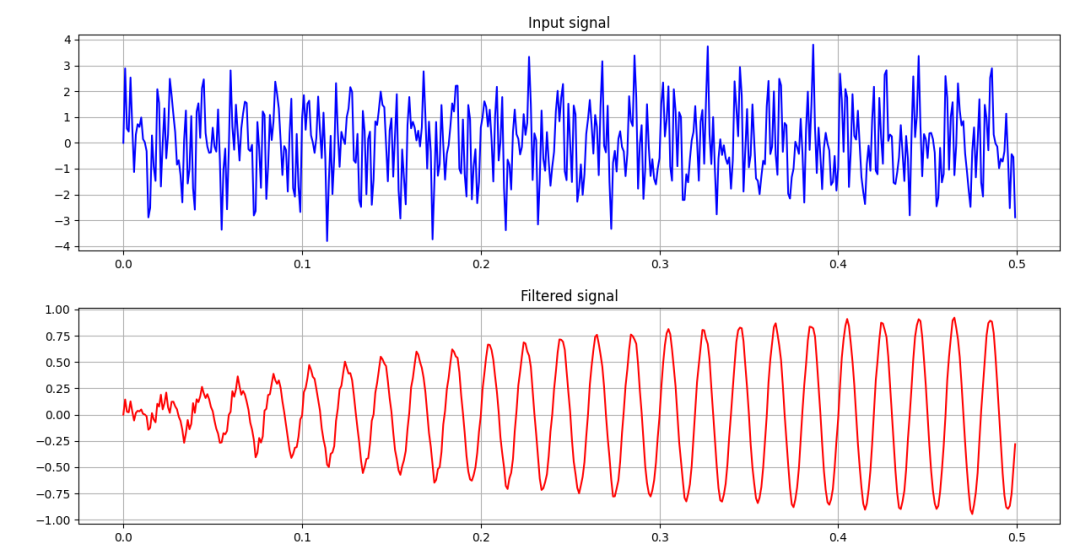
图-7-2   信号滤波前后对比（去除另外一路信号，只有50Hz的信号过滤后）

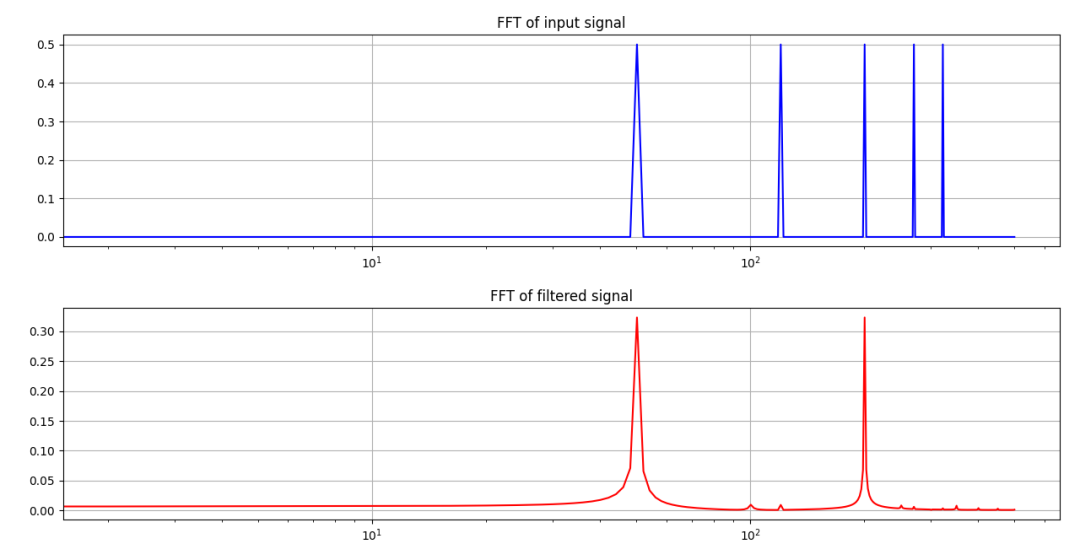
图-8  信号滤波前后的频谱图（留意50Hz和200Hz对应被保留的信号）

图-8中，50Hz及其谐波被保留，而其他频率的信号则被削弱。

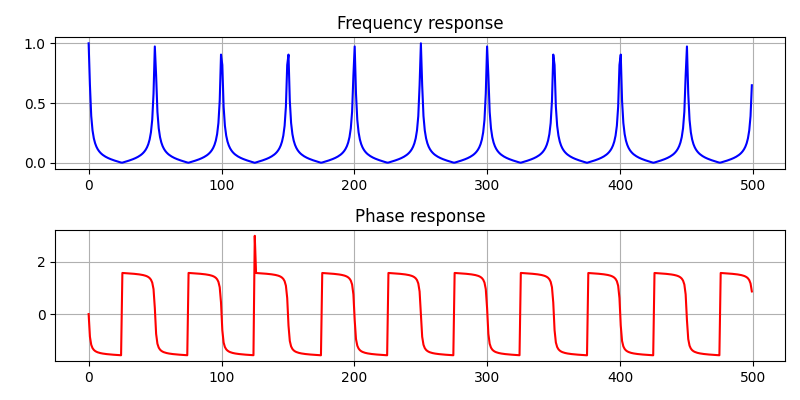
图-9  该梳状滤波器幅、相频率响应图

这是一个基于IIR系统设计的滤波器。所以在相频响应部分可以看到并不是线性相位的。演示代码中，我们可以输出该滤波器的相应系数。对应的系统函数仍然可以简化为（式-2）所示。

图-1所示的陷波梳状滤波器和图-9所示的峰值梳状滤波器的幅频响应来看，两种滤波器的功能刚好是相反的。所有的极点和零点都在演示代码中可以输出。我们可以看一下各自的零点、极点在z平面的分布情况。

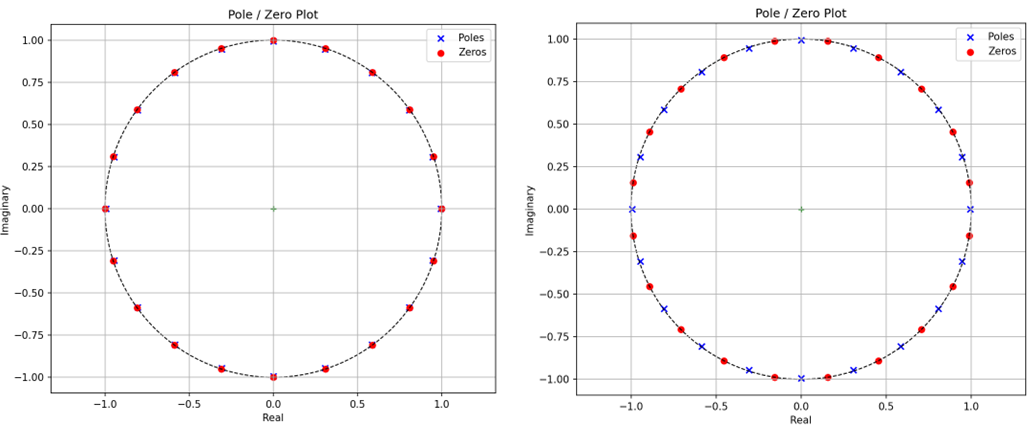
图-10 陷波（左）和峰值（右）梳状滤波器的零极点分布图

Z平面零极点分布特点：零点在单位圆上，极点离单位圆的距离小于1。其中：

陷波梳状滤波器的目标是对一种或几种特定频率的信号进行衰减或者滤除。所以，在对应于这些频率的单位圆上，放置了零点来最大限度地衰减掉这些频率的信号。同时，为了使得在非滤波频率处信号可以通过，所以在零点附近的单位圆内部，放置了极点来抵消在其他频率处零点引起的衰减。至于极点到单位圆的距离，即半径ρ<1，决定了滤波器在滤波频率处的衰减深度以及过渡带的宽度。    

峰值梳状滤波器刚好相反，它的目标是放大一些特定频率的信号，或者在某些频率处衰减。所以，它在滤波频率对应的位置放置了极点来放大这些频率的信号，同时在极点附近的单位圆上放置零点来抵消在其他频率处极点引起的放大。极点离单位圆的距离，即半径ρ<1，决定了滤波器在滤波频率处的放大程度以及过渡带的宽度。

在后面的演示代码中，我们可以看到该处理函数的采样频率是1000Hz。所以这个频谱图也只到500Hz。那为什么不用更高的采样频率？有以下喜忧参半的几点要考虑：

采样频率越高，就意味着同样的时间内应用系统需要更多的缓存资源来保存和处理更多的数据。

其次，按照奈奎斯特采样定理，你的采样频率如果为Fs，则能够有效采样和还原的信号频率上限是Fs/2。所以，当你提高采样频率时，能够处理的信号频率范围也变得更广，可以过滤的基频倍数也越多和越高。

再有需要考虑，是否真的需要更高的采样频率？这完全取决于应用需要。很多情况下，谐波频率越高，对应的能量也越小，在多次谐波之后，对应谐波所附能量几乎可以忽略的情况下，就没有必要再额外增加这些资源。  

虽然梳状滤波器的信号传递架构仍然可以参考下图，不过因为其规律性的梳齿特征的幅频响应可以由（式-2）简化到（式-3）所示，仍然是IIR系统，信号传递过程也可以相应简化。

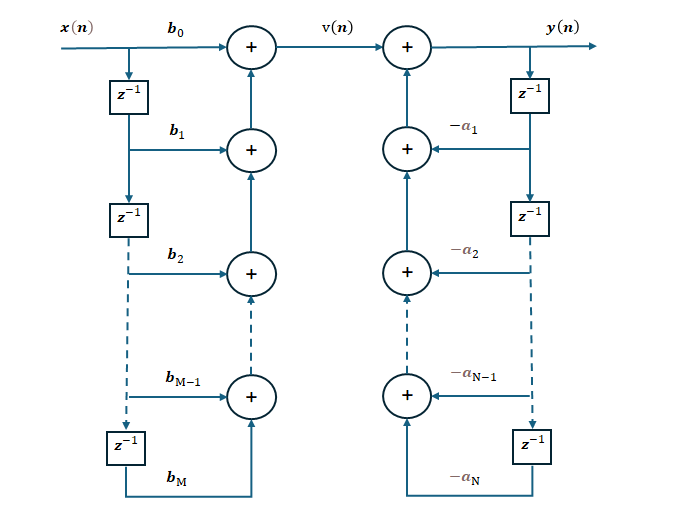
图-11    滤波器的信号传递

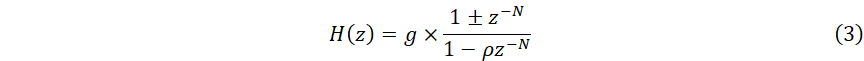
（式-3）中分子对于零点的正负的选择，将取决于我们对所选频率的所需的位置。

如果是“-”号，那么梳状滤波器必有零点对应于直流DC信号和高频段；

如果是“+”号，那梳状滤波器在DC和高频段将没有零点。

在以上两种情况下，对于梳状滤波器的零极点的分布将会有直接影响。实际应用需要根据需要进行调整。了解这些，对于调用现成的函数，也可以提供了解和参考。

理论上，我们可以用陷波滤波器或窄带选频滤波器串并联的方式来搭建梳状滤波器，但是一定要了解这种实现方式对于资源和时延，以及是否线性相位等方面对应用的影响。

4. 小结

在本文中，我们探讨了包括梳状滤波器在内的几种滤波器的设计和应用，以及仿真，同时简单探讨了以下线性相位系统的重要性。在各种传感器的应用过程中，总是会碰到各种状况，我们需要使用者根据实际情况进行应对。

另外，实际应用过程中，还有哪些条件需要考虑的？比如，如果数据采样的时钟因为某种原因并不准有影响吗？有无补偿的方式呢？

安费诺传感器（Amphenol Sensors）提供诸多满足您应用的可靠、准确高精度的传感器，但如果实际应用过程中碰到一些异常的信号，可以和我们一起来分析原因，解决问题，根据实际工况来改善应用。

峰值梳状滤波器模拟测试代码

 

import matplotlib.pyplot as plt
import numpy as np
import scipy.signal as signal
from scipy.fft import fft


# Sampling rate and time vector
fs = 1000.0
t = np.arange(0, 0.5, 1/fs)


# Input signal
freqs = np.array([50.0, 120.0, 270.0, 322.0])
x = np.sin(2.0*np.pi*freqs[:,None]*t).sum(axis=0)


# Design filter
w0 = 50.0 # Frequency to be removed from signal (Hz)
Q = 30.0 # Quality factor
b, a = signal.iircomb(w0, Q, ftype='peak', fs=fs, pass_zero=False)


# Calculate Zeros, Poles & gain of the filter
zeros, poles, gain = signal.tf2zpk(b, a)
print('Zeros: ', zeros)
print('Poles: ', poles)
"""
# 输出零极点
print('Zeros: ', zeros)
for zero in zeros:
    print('Abs of Zero:',abs(zero))
    
print('Poles: ', poles)
for pole in poles:
    print('Abs of Pole:',abs(pole))
"""
print('Gain: ', gain)


# Frequency response
freq, h = signal.freqz(b, a, fs=fs)
amplitude = np.abs(h)
phase = np.angle(h)


# Apply filter
y = signal.lfilter(b, a, x)


# Normalized FFT
N = len(t)
fftx = (fft(x)/ len(t))[:N//2]
ffty = (fft(y)/ len(t))[:N//2]


frequencies = np.linspace(0, fs/2, len(fftx))


# Output to figures
plt.figure(figsize=(8, 6))


# Input signal
plt.subplot(2, 1, 1)
plt.plot(t, x, color='blue')
plt.grid()
plt.title('Input signal')


# Filtered signal
plt.subplot(2, 1, 2)
plt.plot(t, y, color='red')
plt.title('Filtered signal')
plt.grid()
plt.tight_layout()
plt.show()


# FFT of input signal
plt.figure(figsize=(8, 6))


plt.subplot(2, 1, 1)
#plt.semilogx(t*fs, np.abs(fftx))
plt.semilogx(frequencies, np.abs(fftx),color='blue')
plt.grid()
plt.title('FFT of input signal')


# FFT of filtered signal
plt.subplot(2, 1, 2)
#plt.semilogx(t*fs, np.abs(ffty))
plt.semilogx(frequencies, np.abs(ffty),color='red')
plt.title('FFT of filtered signal')
plt.grid()
plt.tight_layout()
plt.show()


# Plot frequency and phase response
plt.figure(figsize=(8, 4))


plt.subplot(2, 1, 1)
plt.plot(freq, amplitude, color='blue')
plt.grid()
plt.title('Frequency response')


plt.subplot(2, 1, 2)
plt.plot(freq, phase, color='red')
plt.grid()
plt.title('Phase response')


plt.tight_layout()
plt.show()


# 极坐标图输出
plt.figure(figsize=(8,8))
plt.scatter(0, 0, marker='+', color='green')
plt.scatter(np.real(poles), np.imag(poles), marker='x', color='blue', label='Poles')
plt.scatter(np.real(zeros), np.imag(zeros), marker='o', color='red', label='Zeros')
# 参数(0,0)代表圆心坐标，1代表半径
circle = plt.Circle((0, 0), 1, fill = False, linestyle='dashed') 
plt.gca().add_patch(circle)


plt.title('Pole / Zero Plot')
plt.xlabel('Real')
plt.ylabel('Imaginary')
plt.legend()
plt.grid()
plt.axis('equal') # equal scaling in both x and y
plt.show()