超声流量传感器信号采样率的影响

我们在之前在《流量传感器(2)—超声流量传感器，相位差和相关性原理》中曾留了一个问题：如果采样频率不一样，模拟的结果会怎么样？不知道大家有没有时间去运行测试一下，反正小编尝试了。测试的结果（但不是最终结论，请根据实际应用进行调整）下文会提到。

在小编上次关于超声流量的相关信号处理的模拟中，用到了插值的方式，不过由于没有经过太多的测试，在后续测试过程中，发现当声速为4500m/s的模拟流体的流速不超过15m/s时，都没有什么问题;但是当模拟的流速超过15m/s之后，两组模拟信号的相位差超过了180°时，获取相关性序列中对应的时间值时，发现取值结果为负数。

相位差180°，这本身没有问题，但是由于数据的相关性处理函数是个偶函数，对称于中点，所以在数据相关性处理中，当两路信号的相位差超过180°前后时，因为两路测试信号是正余弦形式，相当于其中一路信号序列在相对于另外一路信号序列移动的时候，在某个相对处的相关计算结果，可以找到另外一个错位的对方有相同的相关处理结果，然而在查找标识相位偏差所对应的最大值时间序列值时，测试代码优先输出了最左侧编号是负数的相位序列，实际应该输出相关性序列中点右侧的最大值所对应的时间序列值。结果可想而知，计算的流速变成了负数。修改后的代码中，计算流速时，使用的相关性序列是整个相关结果序列的右边部分，就解决了输出流速突然变成负数的问题。

另外，实际的超声波接收信号并不会是从头至尾都是理想的正余弦，因此，我们看到的模拟信号似乎也是太过于理想。这里我们稍微加了点料，让稳定的信号后面加上了快速衰减。

在进行模拟信号相关性处理的时候，之前我们使用的是直接死磕方式的计算，这里调整为快速傅里叶计算(FFT)。

所以，这里我们将模拟代码作了以下调整，顺便作了在不同采样频率下的模拟测量值比较：

在原来的模拟超声波接收信号的生成数据中，加入最后衰减的部分;

在生成的相关性序列中，只取中间点右侧的一半作为分析处理部分;

图像输出时，仍然输出全部的相关性序列;

在生成相关性序列时，需用了FFT的模式(原先的选用的直算的方式);

降低“采样频率”到5MHz，然后采样插值的方式进行相关性处理。

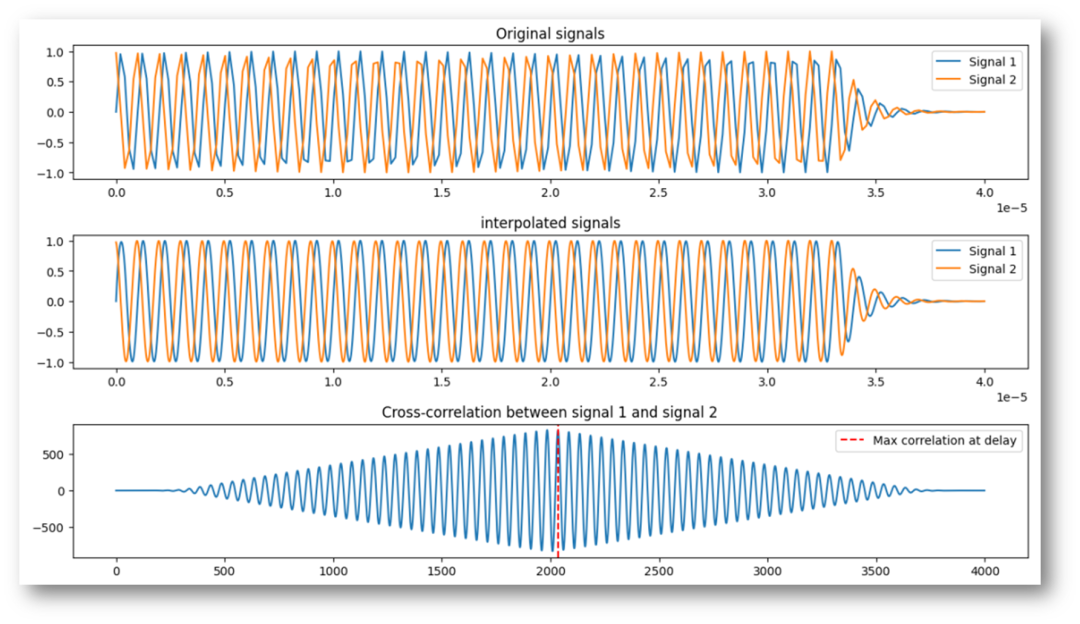
上图模拟的是16m/s下，5MHz采样率，得到的输出值：

T1_0: 4.5617943222309144e-07

Length of t lags: 2000

Ts Delayed cycles: 23 ,

Delayed time: 4.6e-07

degree(相位差，角度): 165.6

Sample time interval(采样间隔时间): 2.0e-08

Estimated velocity: 16.134001423268288(m/s)

不同采样率，不同模拟流速下的模拟输出比较（都有插值）

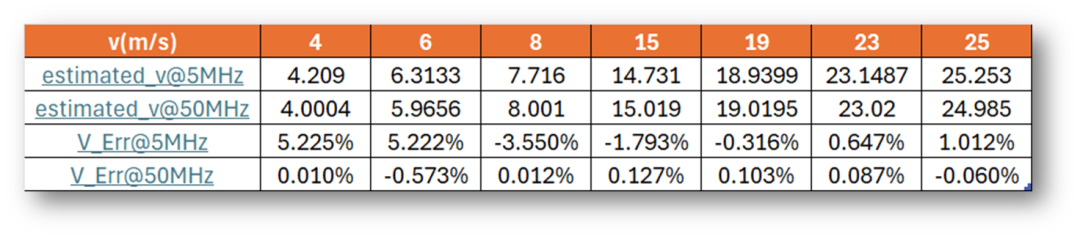
从模拟结果来看，较高的采样率确实可以获得较高的测量精度，而低的采样率，虽然适用了插值提高了测量精度，但是插值运算毕竟是基于我们设定了波形的形态进行的。实际应用，还是要根据实际需求和情况配置相关的软硬件功能。

另外需要说明的是，在整个信号相关性处理的模拟过程中，这里并没有将相关性结果序列归一化后输出，而是使用直接结果的方式。

小编还要留一个问题：如果插值处理中标识插值点数的参数有变化的时候，模拟结果会出现什么变化?欢迎大家测试并留个回复。

修改之后的模拟代码

其中：模拟代码中的噪声部分是被注释掉的

 

 

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import correlate
import math
from scipy.interpolate import interp1d


def cor_demo():
    try:
        # Parameters
        c = 4500    # Sound speed in the fluid in m/s
        d = 0.5     # Pipe diameter in meters
        theta = math.pi / 6     # Angle of the emitted ultrasound wave, in radians. 30 degrees here.
        L = d / math.cos(theta) # The sound path length in meters parallel to the flow direction
        v = 16                  # Fluid velocity in m/s


        f = 1e6     # Frequency of the signal in 1MHz
        T = 1 / f   # Period of the signal in s


        Fs = 5e6        # 采样频率为5MHz
        Ts = 1/Fs       # 采样间隔
        
        # Calculate time delay caused by flow velocity
        time_up = L / (c - v * math.sin(theta))     # Time of flight upstream
        time_down = L / (c + v * math.sin(theta))   # Time of flight downstream
        
        print("T1_0:",time_up-time_down)
        t_delay = 2 * L * v * np.sin(theta) / (c**2 - v**2 * np.sin(theta)**2)
        
        # Time array
        # 返回一个从0到period*T范围内的有num_samples个元素的一维数组，数组中的数值是等间距分布的
        period = 40
        num_samples = period*T/Ts
        t = np.linspace(0, period*T, int(num_samples))
        
        t_max = t.max()
        t_start_decay = t_max * 5/6


        # 定义信号衰减准则 - 衰减系数一般由物质的特性决定
        attenuation_coefficient = 10e5
        
        # Signals
        stationary_s0 = np.sin(2 * np.pi * f * t[t=t_start_decay])* np.exp(-attenuation_coefficient * (t[t >= t_start_decay] - t_start_decay))
        decay_s1 = np.sin(2 * np.pi * f * (t[t>=t_start_decay]-t_delay))* np.exp(-attenuation_coefficient * (t[t >= t_start_decay] - t_start_decay))
        
        #s0 = np.sin(2 * np.pi * f * t)* np.exp(-attenuation_coefficient * t)
        #s1 = np.sin(2 * np.pi * f * (t - t_delay))* np.exp(-attenuation_coefficient * t)  #*2.0 # Signal 1
        
        s0 = np.concatenate([stationary_s0, decay_so])
        s1 = np.concatenate([stationary_s1, decay_s1])
        """
        noise0 = np.random.normal(0, 0.5, s0.shape)
        noise1 = np.random.normal(0, 0.5, s1.shape)
        
        s0 = s0 + noise0
        s1 = s1 + noise1
        """
        # Define interpolation factor
        interp_factor = 10


        # New time vector after interpolation
        t_new = np.linspace(t.min(), t.max(), t.size * interp_factor)
        
        # Create a function based on the original signals, which can be used to generate the interpolated signals
        interp_func_s0 = interp1d(t, s0, kind='cubic')
        interp_func_s1 = interp1d(t, s1, kind='cubic')


        # Generate the interpolated signals
        s0_new = interp_func_s0(t_new)
        s1_new = interp_func_s1(t_new)


        # 计算Cross-correlation，并找到最大值对应的位置
        #correlation = correlate(s1, s0, method='direct', mode='full')  # old
        correlation = correlate(s1_new, s0_new, method='fft', mode='full')
        
        # 找出该序列的长度 len_corr 和其中间点 mid_index
        len_corr = len(correlation)
        mid_index = len_corr // 2
        
        #取序列中间值右边的序列（包含中间值）
        corr_half = correlation[mid_index:]


        #lags = np.arange(-len(s1_new) + 1, len(s1_new)) # Lags array
        lags = np.arange(0, len(s1_new)) # Lags array
        
        print("Length of t lags:", len(lags))
        # Calculate flow speed using the estimated time delay
        # Find the peak of the cross-correlation corresponds to the time delay
        delay = lags[np.argmax(corr_half)]            # 相位差所对应的信号序列值
        
        # 采样时间
        sample_time = (period*T) / len(t_new)
        
        time_delay = delay * sample_time                # 两个信号间的延迟时间
        
        phase_shift = (time_delay / T) * 2 * np.pi      # 由时间延迟换算成的两个信号序列的相位差
        phase_shift_deg = phase_shift * (180 / np.pi)   # 由相位差换成的两个信号序列的角度差
        
        print("Ts Delayed cycles:", delay, ", Delayed time: ", time_delay, "degree:", phase_shift_deg) # 将延迟转换为相位差
        print("Sample time interval:",sample_time)
        # 计算所得的流速
        v_estimated = (math.sqrt((L**2)+(time_delay**2)*(c**2))-L)/(time_delay * math.sin(theta))
        print('Estimated velocity: ', v_estimated)


        # 输出图
        fig, (ax_origin, ax_interpo, ax_corr) = plt.subplots(3, 1, figsize=(12, 8))


        # 原始信号图
        ax_origin.plot(t, s0, label='Signal 1')
        ax_origin.plot(t, s1, label='Signal 2')
        ax_origin.set_title('Original signals')
        ax_origin.legend()


        # 插值后的信号图
        ax_interpo.plot(t_new, s0_new, label='Signal 1')
        ax_interpo.plot(t_new, s1_new, label='Signal 2')
        ax_interpo.set_title('interpolated signals')
        ax_interpo.legend()
        # 互相关图
        ax_corr.plot(correlation)
        ax_corr.axvline(x = len(correlation)//2 + delay, color = 'r', linestyle = '--', label = "Max correlation at delay")
        ax_corr.set_title('Cross-correlation between signal 1 and signal 2')
        ax_corr.legend()


        plt.tight_layout()
        plt.show()
        return
    except Exception as e:
        print("Error:",e)


if __name__=='__main__':
    cor_demo()