

一款超高频带通滤波器的设计方案
调谐/滤波
描述
一、超高频带通滤波器设计
射频滤波器在无线通信系统中至关重要,起到频带和信道选择的作用,并且能滤除谐波,抑制杂散。事实上,对于大多数现代滤波器的设计,射频/微波模拟软件是一个绝对必要的、评估滤波器性能的工具。美国安捷伦(Agilent)公司推出的大型EDA软件Advanced DesignSystem-ADS就是其中的佼佼者,也是国内各大学和研究所在微波电路和通信系统仿真方面使用最多的软件之一。本文在理论设计的基础上,利用ADS软件对耦合微带线带通滤波器进行优化设计,节省了设计时间,提高了方案设计的精度和方案设计的效率。
1、带通滤波器设计-理论设计
1.1 带通滤波器设计-设计指标
耦合微带线带通滤波器的设计指标如下所示:
(1)通带频率范围:902~928 MHz,中心频率为915 MHz;
(2)带内波纹小于3 dB;
(3)阻带损耗:850 MHz以下及950 MHz以上衰减大于40 dB;
(4)带内输入/输出端口反射系数小于-20 dB.
耦合微带线带通滤波器的设计采用FR-4作为基片材料,基片参数为:d=1.6 mm,Er=4.5,tan δ=0.02,铜导体的厚度t=0.035 mm.
1.2 带通滤波器设计-理论计算
当频率达到或接近GHz时,滤波器通常由分布参数元件构成,分布参数不仅可以构成低通滤波器,而且可以构成带通和带阻滤波器。平行耦合微带传输线由两个无屏蔽的平行微带传输线紧靠在一起构成,由于两个传输线之间电磁场的相互作用,在两个传输线之间会有功率耦合,这种传输线也因此称为耦合传输线。平行耦合微带线可以构成带通滤波器,这种滤波器是由1 4波长耦合线段构成,是一种常用的分布参数带通滤波器。当两个无屏蔽的传输线紧靠一起时,由于传输线之间电磁场的相互作用,在传输线之间会有功率耦合,这种传输线称之为耦合传输线。根据传输线理论,每条单独的微带线都等价为小段串联电感和小段并联电容。每条微带线的特性阻抗为Z0,相互耦合的部分长度为L,微带线的宽度为W,微带线之间的距离为S,偶模特性阻抗为Ze,奇模特性阻抗为 Z0.单个微带线单元虽然具有滤波特性,但其不能提供陡峭的通带到阻带的过渡。如果将多个单元级联,级联后的网络可以具有良好的滤波特性。滤波器设计首先要选择适当的低通滤波器原型,滤波器的阶数可以根据950 MHz频率点的衰减大于40 dB的要求确定。利用带通滤波器频率变换公式如下:
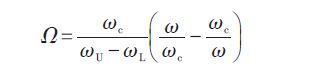
要在低通滤波器原型的相应归一化频率点Ω=2.64处获得40 dB的衰减,滤波器的阶数至少为N=4,则需要采用5节耦合微带线级连。根据设计指标中需要的衰减和波纹,选定采用切比雪夫设计方法,则可知具有3 dB波纹的4阶切比雪夫滤波器的元件参数为g0=1,g1=3.438 9,g2=0.748 3,g3=4.347 1,g4=0.592 0,g5=5.809 5.
耦合微带线带通滤波器中传输线的奇模、偶模通过公共接地板产生耦合效应,并导致了奇模特性阻抗和偶模特性阻抗,其公式分别如下所示:
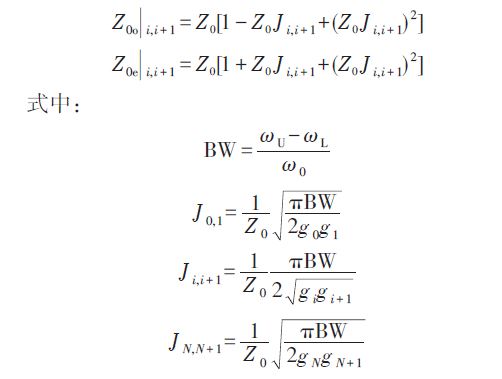
对于平行耦合微带线而言,利用ADS软件中的工具LineCalc,可以进行物理尺寸和电参数之间的数值计算,根据计算所得平行耦合微带线奇模和偶模的特性阻抗,计算平行耦合微带线导体带的角度和间隔距离。由上述特性阻抗,可得微带线的实际尺寸如表1所示。
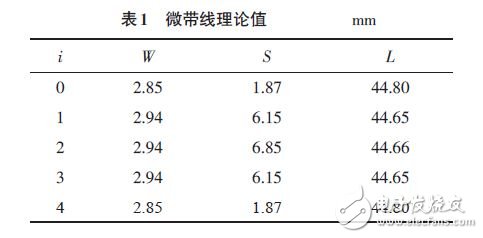
2 带通滤波器设计-ADS 优化仿真
2.1 带通滤波器设计-方案设计的原理图
利用计算所得尺寸,建立如图1所示原理图,并进行仿真。

由图2的仿真结果可以看出,850 MHz及950 MHz以上衰减大于60 dB,符合设计要求,但是902~928 MHz之间的衰减过大,不符合设计指标,需进一步优化。
2.2 带通滤波器设计-优化仿真
方案在进行设计时,主要是以滤波器的S 参数作为优化目标进行优化仿真。S2(1 S12)是传输参数,滤波器通带、阻带的位置以及衰减、起伏全都表现在S21(S12)随频率变化曲线的形状上。S1(1 S22)参数是输入/输出端口的反射系数,由它可以换算出输入/输出端的电压驻波比。
如果反射系数过大,就会导致反射损耗增大,并且影响系统的前后级匹配,使系统性能下降。常用的优化方法有Random和Gradient,随机法通常用于大范围搜索,梯度法则用于局部收敛。因此,在具体的设计中,首先适当放宽各个参数的取值范围,采用随机法进行优化,而后参照之前随机法优化结果,适当缩小各个参数的取值范围,进而采用梯度法再次优化。根据设计指标的要求,优化目标的设置如图3所示。优化后的原理图仿真结果如图4所示。由图3,图4可看出,优化后的尺寸可以满足设计指标的要求。之后可以进行版图仿真。

2.3带通滤波器设计-版图仿真
原理图的仿真实在完全理性的状态下进行的,而实际电路板的制作往往与理论有较大的差距,这就需要考虑干扰、耦合等因素的影响。因此需要在ADS中进一步对版图仿真。
用于生成版图的原理图如图5所示。

版图仿真结果与原理图仿真结果有所不同,它与原理图仿真的方式不同,更为严格,因此很有可能仿真出的结果不符合要求,需返回到原理图进行再次优化之后,再进行版图的仿真,直到仿真结果可以达到设计指标的要求为止。版图的仿真结果如图7所示,由图可以看出,设计出的尺寸符合方案设计指标的要求。

3 带通滤波器设计-结语
射频带通滤波器的传统设计方法大多是通过图表查询和曲线拟合来完成的,不但工作量大,而且设计精度不高。本文在理论设计的基础上,采用ADS软件对射频滤波器进行优化及仿真,进而依据方案设计的结果加工制作射频滤波器器件,既减轻了方案设计者的劳动强度,缩短了设计周期,又提高了方案设计精度和效率。测试结果表明,此方案中所运用的射频滤波器设计方法是可行的和有效的。
二、带通滤波器设计-宽带通滤波器

形成宽的带通滤波器,可以通过简单的级联高通和低通部分,一般是简单的设计和性能的选择,尽管这种电路可实现可能的电路数。要形成一个± 20 dB / decade的带通滤波器,一阶高通和一阶低通部分级联;一个± 40 dB /十的带通滤波器,二阶高通滤波器和一个第二阶低通滤波器串联,依此类推。这意味着,带通滤波器的顺序是由高通和低通滤波器,它由秩序的约束。

± 20 dB /十宽的带通滤波器一阶高通滤波器和一阶低通滤波器组成,如图所示。(一)。其频率响应如图所示,(B) 。
三、带通滤波器设计-宽带通滤波器
形成宽的带通滤波器,可以通过简单的级联高通和低通部分,一般是简单的设计和性能的选择,尽管这种电路可实现可能的电路数。要形成一个± 20 dB / decade的带通滤波器,一阶高通和一阶低通部分级联;一个± 40 dB /十的带通滤波器,二阶高通滤波器和一个第二阶低通滤波器串联,依此类推。这意味着,带通滤波器的顺序是由高通和低通滤波器,它由秩序的约束。 频率响应宽带通滤波器 ± 20 dB /十宽的带通滤波器一阶高通滤波器和一阶低通滤波器组成,如图所示。(一)。其频率响应如图所示,(B) 。

一个狭窄的带通滤波器,采用多重反馈描绘图。该过滤器采用只有一个运算放大器,如图所示。在迄今为止所讨论的所有过滤器相比,这种过滤器下面给出的一些独特的功能。
1。它有两条反馈路径,这是它被称为多反馈滤波器的原因。
2。该运算放大器是用来在反相模式。
一个狭窄的带通滤波器的频率响应图(二)所示。
一般来说,窄的带通滤波器是专为特定值的中心频率f c 和Q 或 F C和BW 。电路元件决心从以下几个关系。为了简化设计计算每个C 1和C 2可采取平等为C。
R 1 =Q/2Π C CA f
R 2 =Q/2Π C C(2Q 2, 一个 F )
和R 3 = Q /Π C ?
一个 F ,是在中心频率的增益,并给予一个f = R 3 / 2R 1
增益然而, 一个 F 一个 F < 2 Q 2必须满足的条件 。
多反馈滤波器的中心频率 F C可以改变一个新的频率 F C“不改变,增益或带宽 。这是简单地通过改变R 2 R“ 2,所以 ?“ 2 = R 2 [ C / F“ C ] 2。
-
一阶带通滤波器电路图原理2023-12-01 10633
-
使用运放做高频带通滤波器时候,哪个参数对滤波器影响比较大,该如何选择运放?2024-08-16 301
-
分享一款不错的新型微带带通滤波器设计2021-04-07 2208
-
带通滤波器设计2008-12-01 5896
-
SN测量中使用的音频带通滤波器电路图2009-07-16 1254
-
音频带通滤波器2009-09-16 5960
-
频率可调音频带通滤波器2009-09-17 1970
-
用于测量S/N的音频带通滤波器2010-05-13 1735
-
创新双频带带通滤波器设计2012-05-03 3010
-
中心频率可调节的低频带通滤波器设计与实现2017-01-07 1089
-
新型的三频带通滤波器设计方法2017-12-05 907
-
带通滤波器电路图大全(三款带通滤波器电路设计原理图详解)2018-03-26 324672
-
采用枝节加载谐振器设计的双频带通滤波器2021-11-08 987
-
带通滤波器的带宽由谁确定的2023-02-25 5064
-
带通滤波器的通频带计算方法2023-11-06 5777
全部0条评论

快来发表一下你的评论吧 !

