基于FPGA的通用位同步器设计方案

　　本文主要是先阐述传统Gardner算法的原理，然后给出改进后的设计和FPGA实现方法，最后对结果进行仿真和分析，证明该设计方案的正确、可行性。

　　0 引言

　　数字通信中，位同步性能直接影响接收机的好坏，是通信技术研究的重点和热点问题。通信系统中，接收端产生与发送基带信号速率相同，相位与最佳判决时刻一致的定时脉冲序列，该过程即称为位同步。常见的位同步方法包括滤波法和鉴相法。滤波法对接收波形进行变换，使之含有位同步信息，再通过窄带滤波器滤出，缺点是只适用于窄带信号。最为常用的位同步方法是鉴相法，包括锁相法和内插法两种。锁相法采用传统锁相环，需要不断调整本地时钟的频率和相位，不适合宽速率范围的基带码元同步。而内插法则利用数字信号的内插原理，通过计算直接得到最佳判决点的值和相位。

　　Gardner算法即是基于内插法的原理，通过定时环路调整内插计算的参数，从而跟踪和锁定位同步信号，该算法的优点在于不需要改变本地采样时钟，可以适应较宽速率范围内的基带信号，因而具有传统方法不可替代的优势。Gardner算法的实现方法，为算法的应用提供了基础。Farrow结构非常适合实现Gardner算法的核心，即内插滤波器部分，其优点是资源占用较少，且滤波器系数实时计算，便于内插参数调整。定时误差检测，但在定时误差检测时需要信号中存在判定信息，并且对载波相位偏差敏感。不足进行了改进，提出了GA-TED（Gardner Timing Error Detection）算法，其优点是不需要预知判定信息，且独立于载波同步，并且适合FPGA 实现。改进的Gardner 算法，并将其应用于M-PSK 系统。提高了Gardner 算法的抗自噪声能力，即降低了对本地时钟的要求。

　　本文基于FPGA 平台并采用Gardner 算法设计，其中，内插滤波器采用Farrow 结构，定时误差检测采用GA-TED算法。同时对传统Gardner算法结构进行了改进，使环路滤波器和NCO的参数可由外部控制器设置，以适应不同速率的基带码元，实现通用的位同步器的设计方案。此外，本设计方案还对FPGA 代码进行了优化，节省了大量硬件资源。最后进行了仿真和分析，给出了仿真结果，证实了该方案的可行性。

　　1 传统Gardner 算法与改进

　　1.1 传统Gardner算法基本原理

　　传统Gardner算法结构如图1所示。

　　

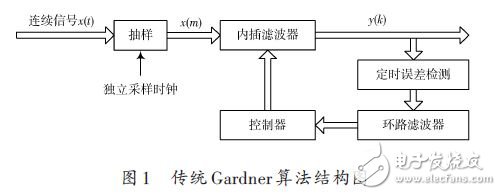
　　在图1中，输入的连续时间信号x（t） 码元周期为T，频带受限。在满足奈奎斯特定理的条件下，接收端采用独立时钟对x（t） 进行采样。内插滤波器计算出内插值y（k），送至定时环路进行误差反馈和参数调整，并与控制器输出的位同步脉冲BS一起送往解调器的抽样判决器。

　　定时环路包含定时误差检测、环路滤波器和控制器。定时误差检测提取插值时刻和最佳判决时刻的误差；该误差经环路滤波器滤除高频噪声后送给控制器；控制器计算插值时刻（即为位同步信号的2倍频）和误差间隔。插值时刻和误差间隔用于调整内插滤波器的系数，使插值时刻尽可能与最佳判决点同相，最终实现位同步信号的提取。

　　1.2 改进的Gardner算法结构

　　从上节可以看出，传统Gardner算法无法满足较宽速率范围基带信号的位同步要求。为实现该要求，本设计在FPGA 平台的基础上，对算法实现结构进行了改进，改进结构如图2所示。

　　

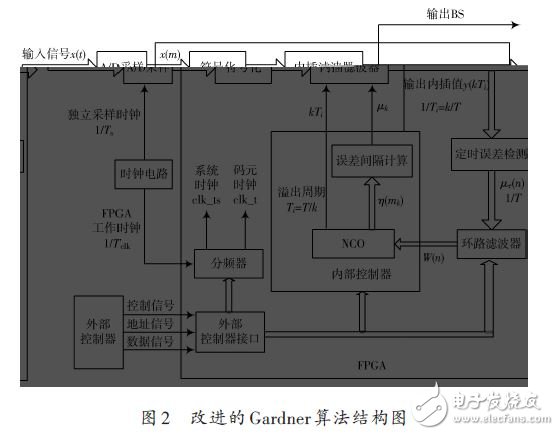
　　图2中，内插滤波器采用Farrow结构的FIR 滤波器实现，滤波器系数实时计算；定时误差检测采用独立于载波且采样点较少的GA-TED 算法；环路滤波器、内部控制器可由外部控制器设置参数，基带码元速率变化时，相应参数可以随之变化。因此，本设计可以满足位同步器的通用性要求。

　　该同步器工作过程如下：外部控制器根据基带码元速率设置相应参数，通过外部控制器接口将控制、地址和数据信号分别送往分频器、环路滤波器和内部控制器。时钟电路分别提供采样时钟和FPGA 时钟，FPGA工作时钟在片内通过分频器产生所需频率的时钟，供FPGA 各模块使用。输入连续时间信号x（t） 经由独立时钟控制的ADC 进行采样，转换为8 位数字信号送至FPGA 内，符号化后变为有符号数字序列，送入内插滤波器模块。内插滤波器根据输入信号的采样值和内部控制器给出的参数μk，在每个插值时刻kTi 计算出最佳判决点的内插值y（kTi）。定时误差检测计算出误差μτ （n），输出至环路滤波器。环路滤波器依据当前的参数设定，滤除噪声并将误差信息送给内部控制器。内部控制器以NCO为核心，根据处理后的误差信息和设定的频率字参数调整插值时刻kTi，使之尽可能接近最佳判决时刻，并输出位同步脉冲BS，同时计算出误差间隔μk 送给内插滤波器，进行内插值计算，最终完成定时信息的恢复。

　　2 FPGA设计

　　2.1 整体结构设计

　　根据图2的算法结构，FPGA设计采用模块化方式，整体结构的顶层图如图3所示。

　　从图3可以看到，该设计包含分频器（DIV_FRE）、符号化（SYM）、内插滤波器（INTERPOLATION）、定时误差检测（TED）、环路滤波器（LPF）、内部控制器（INTER_CTL）和外部控制器接口的时序电路（EXTER_CTL）共7个模块。其中，分频器由片外晶振提供时钟输入，分频后为片内其他模块提供相应时钟。其中码元时钟的分频系数可由外部控制器通过接口进行设置。符号化是将A/D采样产生的无符号数转换为有符号数，以便后续模块进行带符号的运算。

　　外部控制器接口的时序电路将外部控制器送来的控制信号（ALE和RD）、地址信号（P2.0、P2.1）和数据信号（P0口）、转换为FPGA 内分频器、环路滤波器和NCO的使能信号和参数，实现对位同步器各参数的设置。

　　分频器、符号化和外部控制器接口模块实现较为简单，不再赘述。而内插滤波器、定时误差检测、环路滤波器和内部控制器的实现较为复杂，且本设计通过采用相应算法和改进结构，实现了位同步器的通用性。本文将详细阐述这些模块的设计。

　　

　　2.2 模块详细设计

　　2.2.1 内插滤波器设计

　　内插滤波器是完成算法的核心，它根据内插参数实时计算最佳判决点的内插值，即：

　　

　　式中：mk 为内插滤波器基点索引，决定输入序列中哪些采样点参与运算，它由插值时刻kTi 确定；μk 为误差间隔，决定了内插滤波器的冲激响应系数［1］.kTi 和μk 的信息由内部控制器反馈回来。

　　本设计的内插滤波器采用基于4 点分段抛物线多项式的Farrow结构实现。将式（1）变换为拉格朗日多项式，即令：

　　

　　根据式（2）和（3），内插滤波器程序实现结构如图4所示。

　　从图4可以看到，该结构由1个移位器、5个触发器、 8个相加器、2个乘法器组成，比直接型FIR节省10个乘法器、4个相加器的资源。其中，除以2的运算采用数据移位实现，避免使用除法器。输入的8位数据 x，计算后得到10位的内插值y 输出。由于内部所有寄存器经计算后，均采用最小位数，有效地减少了Logic Elements资源的占用。

　　

　　2.2.2 定时误差检测设计

　　定时误差检测程序采用独立于载波相位偏差的GA-TED算法。该算法每个符号周期只需要两个插值，每个码元周期输出一个误差信号μτ （n） ，即：

　　

　　其中，y（n） 表示第n 个码元选通时刻的内插值，前后两个内插值的插值代表误差方向；y（n - 1 2） 表示第 n 个和第n - 1 个码元的中间时刻内插值，代表误差大小。

　　FPGA实现时，为避免乘法运算，采用y（n） 和y（n - 1）的符号来代替实际值［8］，即采用式（5）计算误差信息：

　　

　　根据式（5）进行程序设计，误差的正负方向判断采用case 语句，当y（n） 和y（n - 1） 的符号位分别为“0”和“1”时，y（n - 1 2）的符号位不变；当符号位分别为“1”和“0”时，y（n - 1 2） 的符号位取反；当符号位为“0”“0”或“1”“1”时，令输出的μτ （n） = 0.TED程序在1 Ti 的时钟控制下进行运算，最终得到29位误差数据，并以1 T 的速率即码元速率输出至环路滤波器电路。

　　2.2.3 环路滤波器设计

　　本文对Gardner算法中的环路滤波器进行了改进，根据通用位同步器的要求，采用二阶数字滤波器，并且开放滤波器参数（C1，C2 ） 和使能（c_en）端口，当码元速率变化时，通过外部控制器来改变参数，实现滤波器的通用性。滤波器结构如图5所示。

　　

　　从图5可以看到，滤波器的输出为：

　　

　　式中：Ko Kd 为环路增益；ζ 为阻尼系数，取ζ =0.707;T 为采样时间间隔，即相位调整间隔；ωn 为无阻尼振荡频率。

　　为减少资源占用，环路滤波器中的乘法运算均采用移位方式实现，处理后的误差信息送给内部控制器。

　　2.2.4 内部控制器设计

　　内部控制器根据定时误差信息，调整插值频率1 Ti和误差间隔μk ，并输出位同步脉冲BS，它包含NCO（Numerically Controlled Oscillator）和误差间隔计算两部分。该程序提供接口（频率字fw 和使能端fw_en），外部控制器可以通过该接口输入参数。

　　本设计中NCO 采用与文献［10］类似的DDS（DirectDigital Synthesis）结构，其频率控制字Fw 可由外部控制器设置，其结构如图6所示。

　　图6中，M 为频率控制字位数，N 为相位累加器和相位寄存器的位数。这里取M = N = 23，采用递减型的NCO，归一化后相位累加器的累加值为：

　　

　　式中：Fw 为频率控制字；W （mk ） 为环路滤波器输出的误差信号，二者由环路滤波器提供，决定了NCO的溢出周期。其中，当：

　　

　　

　　NCO 溢出信号即为提取出的位同步信号的2 倍频（2BS），经2分频后可以得到位同步脉冲（BS）输出，2BS同时作为内插滤波器和误差间隔计算的使能信号。

　　误差间隔μk 在NCO 溢出后的下一个Ts 时刻进行计算，环路锁定时：

　　

　　将其截断为8位数据送给内插滤波器。

　　本设计同时对代码进行了优化，数据有效位的截取、内插滤波器的结构优化、乘法采用移位计算代替等措施，有效地节省了硬件资源，优化前和优化后的资源占用情况对比见表1.

　　

　　3 仿真和分析

　　3.1 Matlab仿真

　　本文采用Matlab对算法进行理论仿真，输入采样值x（m） 为［-1，1］之间的随机码，采样频率上限为20 MHz，令码元速率分别为2 Kb/s，600 Kb/s，10 Mb/s，环路滤波器、内部控制器参数随码元速率变化。取内插滤波器的插值输出y（kTi） 做散射图分析，验证对不同速率的基带信号，内插值是否接近最佳判决值，如图7所示。

　　从图7可以看出，在基带速率和采样率满足奈奎斯特定理的条件下，该仿真输出的内插值均集中在理想值 -1和1周围，虽然有一定的模糊，且频率越高，模糊程度越大，但码元判决阈值在0值点，所以判决值无需严格为±1，该图表明对于较宽速率范围内的基带信号，输出的插值均能够较好地用于码元判决，即算法正确。

　　3.2 FPGA仿真

　　在Quartus下对本设计进行仿真。基带信号采用M 序列，由FPGA生成，令基带码速率分别为2 Kb/s，600 Kb/s，1 Mb/s，同时分频器、NCO 及环路滤波器参数也做相应设置，仿真结果如图8所示。

　　

　　

　　在图8中，x为基带码元序列，y为内插值输出，clk_t为基带码元时钟，clk_bs为提取出的位同步信号。从图中可以看到，clk_bs经过定时环路调整，其上升沿逐渐向clk_t的下降沿（即最佳判决点）靠近，且随着基带码元速率的变化，clk_bs也会随之变化，但其中心频率与clk_t相同，相位与最佳判决点相差不超过半个码元周期，可以进行码元判决，这表明本设计对2 Kb/s~1 Mb/s内的基带信号，均可实现位同步。

　　4 结语

　　本文提出了一种基于FPGA的通用位同步器的设计方案。该设计方案中的同步器在传统Gardner 算法的基础上进行了改进，其中，内插滤波器采用Farrow结构，定时误差检测采用GA-TED算法，环路滤波器和内部控制器参数可由外部控制器设置，因而实现了较宽速率范围内基带码元的位同步。仿真结果表明，该方案占用FPGA资源较少，并且在实际应用中具有可靠有效性。