

一种基于BOC信号的导航发射信道预失真方案
通信设计应用
描述
0 引言
BOC调制信号的频谱分裂在中心频点的两侧,有利于避开与中心频点信号频谱的相互重叠,从而减小信号间的相互干扰,以实现频段共用。此外,BOC调制信号比BPSK调制信号的相关函数主瓣更窄,它具有更高的码跟踪精度和更强的抗多径干扰能力。由于BOC调制的独特性使其在新一代全球卫星导航系统中倍受青睐。
BOC调制信号经过导航卫星发射信道时,由于各个器件的非理想特性将会使其产生一定程度的失真,致使导航系统的性能会受到一定的影响。目前,国内外对此已有相关的研究。文献主要分析Galileo的几个候选BOC 调制信号特性,其中BOC 调制的非线性特性主要是采用固态功率放大器(SSPA)来仿真,分析了输入功率回退(IBO)为0 dB时,BOC调制方式的相关损耗。文献主要分析Galileo的几个候选BOC调制信号的跟踪精度受到线性和非线性失真的影响,分析了由于滤波器带宽的限制而带来的功率损耗和相关损耗。文献主要分析星上高功放对BOC 及其衍生信号的失真影响,主要分析了带宽限制和非线性效应带来的联合影响。
非线性失真对卫星导航系统性能的影响主要在于:引起信号幅度、相位失真,使星座图发生压缩偏转,致使接收方判决检测受很大影响,引起带内失真;产生大量的互调失真和谐波失真,信号频谱扩展产生的邻道干扰(ACI),产生带外失真。因此,对卫星导航信道的非线性补偿研究显得尤为重要。但是,目前国内外大部分只是针对非理想卫星信道对BOC信号的影响进行了研究,对于消除这种影响的研究却甚少。
自适应数字预失真技术是补偿非线性失真最好的方法之一,它通过在非线性器件前构造非线性失真的逆特性来达到线性化目的。随着信息速率的增加,信号带宽不断增加,导航信道不仅具有非线性特性,其记忆效应也越来越明显。对于有记忆效应的非线性失真,若仍采用传统的无记忆预失真技术,非线性补偿机制可能失效或是效果不佳。因此,研究记忆非线性失真的线性补偿技术具有非常重要的意义。
本文即是对BOC 信号进行预失真仿真分析,对导航卫星发射信道进行建模等效,提出将发射信道等效为Wiener-Hammerstein模型,并设计了一种针对此模型的基于直接学习结构的自适应LMS 预失真方案,通过仿真结果可以看出该预失真方案可以很好地消除导航信道对BOC信号的失真影响。
1 导航发射信道模型
根据目前已有的国内外导航卫星发射信道模型,可归纳总结出导航卫星发射信道的等效简化模型如图1所示。

如图1所示,前置滤波器和后置滤波器均采用线性FIR 滤波器,高功放采用行波管功率放大器(TWTA)模型。行波管大功率放大器AM/AM变换表现为幅度非线性失真,AM/PM变换表现为相位非线性失真,通常可用无记忆Saleh幅值-相位模型进行模拟,即:
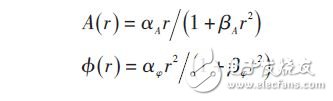
当综合考虑前置滤波器、TWTA、后置滤波器时,记忆效应不能忽略,此时,导航发射信道实际上可以等效为有记忆Wiener-Hammerstein 模型,即线性时不变系统(LTI_1)后串连一个无记忆非线性模型(NL)后再串连一个线性时不变系统(LTI_2),该模型常用于描述卫星通信中的大功率功放。其结构图如图2所示。

其中每个模块用数学表达式表示为:
综合每个模块可得Wiener-Hammerstein 模型的数学表达式为:

式中:K 表示功放模型的多项式阶数;L 表示功放的记忆深度。
2 预失真方案
预失真方法通常分为查找表预失真和多项式预失真,因多项式预失真较节省RAM存储单元,且收敛速度快,本文选用多项式预失真方法。基于多项式的预失真有直接学习结构和间接学习结构两种,其中直接学习结构的结构简单,算法收敛后能达到比较好的预失真效果,预失真器参数不受功放非线性系统输出端噪声的影响,可直接更新预失真器的参数。但需首先设定PA模型,根据模型估计出放大器的非线性传递函数,再求出逆函数作为预失真器的传递函数。由第一部分导航发射信道模型的描述可知,导航发射信道的主体部分可等效为有记忆Wiener-Hammerstein模型,符合直接学习结构中要求模型已知的条件,所以本文采用直接学习结构。
图3即为基于直接学习结构的预失真框图,在这个结构中,x(n) 为n 时刻的输入信号,y(n) 为功放的输出信号,其中整个系统所期望的响应为d(n),图中的线性放大倍数为G,当e(n) = d(n) - y(n) 在算法收敛于e(n) = 0时,则功放的输出为输入信号的线性,并且有y(n) = G*x(n)。

针对本文建立的导航发射信道为一有记忆非线性信道,为补偿非线性,其逆特性也应具有记忆效应。基于记忆多项式的预失真通常可以很好地补偿有记忆效应的非线性模型,记忆多项式模型如下:

式中:K 为记忆多项式阶数,补偿效果与多项式阶数有关,一定程度下,阶数越高补偿效果越好,但同时会增加算法的复杂度,针对相同的输入信号,预失真多项式最佳阶数的选择与功放模型有关。Q 为记忆深度,记忆深度越大,预失真效果也越明显,功放线性度改善越好,但太大也会实现困难,要根据实际需要选取合适的。
akq 是预失真器的多项式系数,其估计精度决定了预失真器的性能,系数更新可以通过自适应算法获得。
LMS算法是一种梯度最速下降算法[8],在算法迭代过程中,它不需要计算相应的相关矩阵,也不需要进行矩阵运算,因此具有每次迭代时的计算量最小,所用的存储空间最少,容易以硬件实现,便于调试等优点,被广泛应用。其算法流程图如图4所示。

估计的误差信号为:

可以看出,由当前时刻的权系数矢量和以误差函数为比例因子的输入矢量可以得到下一时刻的权系数矢量。预失真器通过以上给定的算法,不断更新预失真器的参数,以达到对信道记忆非线性逆特性的逼近。
3 仿真结果与分析
本文采用BOC(14,2)信号进行仿真验证。码延迟和载波初相位均为0,Saleh 模型使用经典模型参数[2.158 7 1.151 7 4.003 3 9.104 0],FIR 滤波器的系数取[0.769 2 0.153 8 0.076 9]。多项式阶数取5,记忆深度取3.图5(a)为原始输入的BOC(14,2)信号的星座图,图5(b)为经过滤波器的线性、功放的非线性等失真后的星座图,输入信号为BOC 信号,带宽较宽,卫星信道呈现出有记忆的非线性特性,理想星座经过信道后,如果不采用任何补偿措施,可看到星座图已出现扭曲,幅度失真且出现相位偏转。图5(c)为加入预失真之后的星座图,可看到星座图已得到改善,接近理想星座。

图6 为BOC(14,2)信号在预失真前后系统输出信号和原信号的功率谱密度,明显可见,在经过卫星发射信道后信号不仅被放大且出现严重的带外频谱扩展,会造成相邻信道干扰(ACI),引起带外失真。在信号经过预失真后,明显降低了BOC信号的带外频谱扩展,减少了相邻信道干扰(ACI),大大减小了带外失真。

4 结语
基于当前导航卫星发射信道的记忆非线性对BOC信号的失真影响,本文通过对导航卫星发射信道的等效简化建模的研究,提出将发射信道的主体部分(HPA以及前后置滤波器)等效为有记忆Wiener-Hammerstein模型,并设计出一种适合此模型的基于直接学习结构的自适应LMS预失真方案,用于消除这种失真影响。仿真结果表明,该方案能有效抑制BOC信号的带外频谱扩展,减小带外失真,优化星座图,减小带内失真,可以很好地消除导航信道对BOC 信号的失真影响,在卫星导航系统中有着重要的意义。
-
请问怎样去设计一种数字预失真校正系统?2021-05-26 1764
-
求一种新的混合预失真器的设计2021-04-22 964
-
求一种数字信道化IFM接收机的高效实现方案2021-02-23 1639
-
W-CDMA模拟预失真功率放大器的线性化技术设计2019-07-15 2477
-
插入式短波预失真器的设计与实现2018-01-18 954
-
一种有源射频模拟预失真器2017-12-29 1085
-
基于滤波器预失真的导航信号监测技术2017-11-07 1297
-
一种QRD-LS与单路计算方法的预失真方法2017-11-01 1015
-
一种新型基于Strobe相关的BOC信号多径抑制算法2013-06-25 986
-
可修正RF信号的RF预失真2011-08-02 4678
-
一种改进的联合信源信道编码算法2011-05-16 698
-
一种新的分数阶记忆多项式预失真器2009-11-10 866
-
一种新的记忆多项式预失真器2009-08-08 4323
全部0条评论

快来发表一下你的评论吧 !

