DSP in FPGA：FIR滤波器（二）

　　这一节主要讲解一下转置型FIR滤波器实现。

　　FIR滤波器的单位冲激响应h（n）可以表示为如下式：

　　

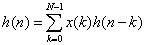
　　对应转置型结构的FIR滤波器，如图1所示，抽头系数与上一节中讲解直接型FIR滤波器的实例相同，滤波器阶数为10。

　　

　　图1

　　可以发现转置型结构不对输入数据寄存，而是对乘累加后的结果寄存，这样关键路径上只有1个乘法和1个加法操作，相比于直接型结构，延时缩短了不少。

　　综合得到结果如下：

　　Number of Slice Registers： 1

　　Number of Slice LUTs： 18

　　Number of DSP48E1s： 11

　　Minimum period： 4.854ns{1} （Maximum frequency： 206.016MHz）

　　关键路径延时报告如图2所示，其中乘累加操作延时Tdspdck_A_PREG_MULT 2.655ns；另外还有一项net delay居然有1.231ns，如此大是因为fanout=11，仔细研究可以发现在h（n）表达式中x（n）与所有11个抽头系数进行了乘法操作，因此fanout达到了11，这也是转置型FIR滤波器的缺点：输入数据的fanout过大。

　　

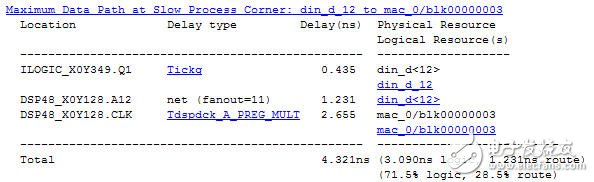
　　图2

　　线性相位：

　　与直接型结构相同，由FIR滤波器的线性相位特征，转置型结构的FIR滤波器也可优化，如图3所示为线性相位FIR滤波器转置型结构，总共11个抽头系数，其中5对系数两两相同，因此可以省去5个乘法器，采用6个DSP资源实现转置型FIR滤波器。

　　

　　图3

　　流水线实现：

　　为了进一步缩短关键路径的延时，将乘法器和加法器逻辑分割开，中间加入流水线级，结果如图4所示，在线性相位结构的基础上，加入一级寄存器，这样最大限度上优化时序。

　　

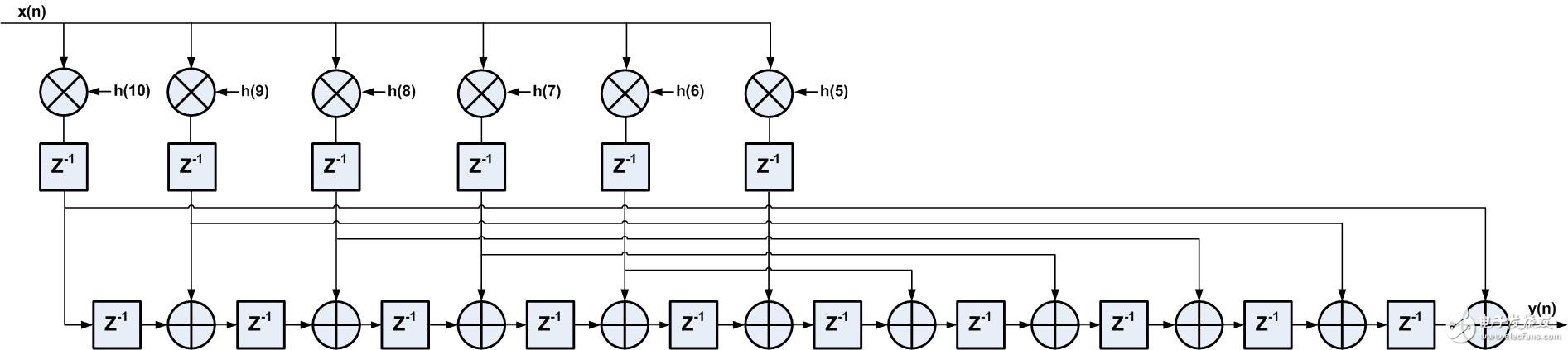
　　图4

　　综合得到结果如下：

　　Number of Slice Registers： 355

　　Number of Slice LUTs： 340

　　Number of DSP48E1s： 6

　　Minimum period： 3.861ns{1} （Maximum frequency： 259.000MHz）

　　如图5所示为与图2中相对应路径的延时报告（图2由ISE的Timing Analysis工具产生，图5是由PlanAhead的Timing Analysis工具产生），其中由于采用线性相位结构，输入信号的fanout只有6，延时从原先的1.231ns减小到1.01ns；并且分隔乘法器和加法器逻辑之后，关键路径上只有乘法器的延时：1.42ns。

　　

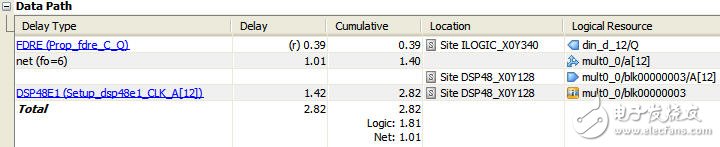
　　图5

　　脉动型FIR滤波器是对直接型的升级，在每个操作后都加入流水线级，每个动作都打一拍，就跟心脏跳动一样，因此称为脉动型，这种结构非常适用于高速数据流的处理。如图1所示为脉动型FIR滤波器结构。

　　

　　图1

　　与直接型结构不同的是，输入数据到下一个处理单元都需要打2拍，这是为了使乘法后的累加数据同步，下面推导验证：

　　x（n）为输入数据，yt（n）为直接型结构的输出

　　yt（n）=x（n）h（0）+x（n-1）h（1）+x（n-2）h（2）…x（n-10）h（10）

　　ys（n）为脉动型结构的输出，如图1中有P1、P2…P10共10个节点

　　P1=x（n-4）h（0）

　　P2=（P1 + x（n-5）h（1））*Z-1=x（n-5）h（0） + x（n-6）h（1）

　　…

　　P10=（P9 + x（n-23）h（10））*Z-1

　　ys（n）=x（n-14）h（0） + x（n-15）h（1） + … + x（n-23）h（9）+ x（n-24）h（10）

　　由ys（n）和yt（n）的表达式，可以推导出ys（n）=yt（n-14）

　　因此脉动型FIR滤波器的延迟较大

　　如图2所示为11抽头系数脉动型FIR滤波器FPGA实现结构（实例与前几节相同），穿了一层“衣服”，采用Xilinx FPGA中的DSP48E1 实现，基本处理单元中的操作都可在一个DSP48E1中完成，输入数据经过DSP48E1中寄存2拍后通过ACOUT输出，直接连接到下一个 DSP48E1中的ACIN端口，累加输出PCOUT直接连接到下一个DSP48E1中的PCIN端口，这些连接都没有经过FPGA的Fabric连线逻辑，而是通过DSP Block的内部走线连接，这样实现能够缩短路径的延时。

　　

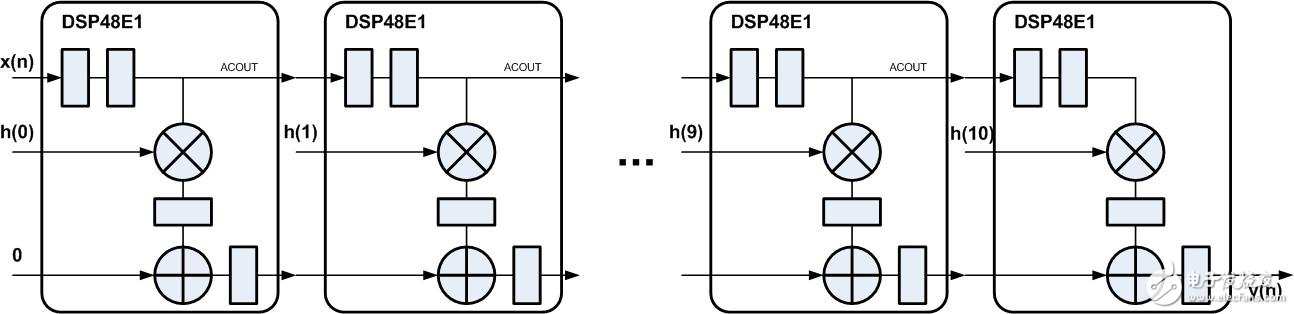
　　图2

　　编写了相关代码，综合结果如下：

　　Number of Slice Registers： 4

　　Number of Slice LUTs： 19

　　Number of DSP48E1s： 11

　　Minimum period： 3.006ns{1} （Maximum frequency： 332.668MHz）

　　线性相位实现：

　　与前几节相同，由于FIR滤波器的线性相位特性，相对应有线性相位的实现结构，如图3所示，利用DSP48E1中预加器实现乘法前的加法操作。对于脉动型 FIR滤波器的线性相位结构有很多注意点，其中预加器数据的配对，常规情况下，此例中应是x（n）和x（n-10）、x（n-1）和x（n-9）、 x（n-2）和x（n-8）、x（n-3）和x（n-7）、x（n-4）和x（n-6），而图3中结构，加入了延时11的移位寄存器，预加器配对的数据为 x（n-2）和n（n-12）、x（n-4）和x（n-12）、x（n-6）和x（n-12）、x（n-8）和x（n-12）、x（n-10）和x（n- 12），可以发现预加器配对数据中有一个数据始终是x（n-12），但是每一个配对数据的相对延时与常规情况下相同：10、8、6、4和2。

　　

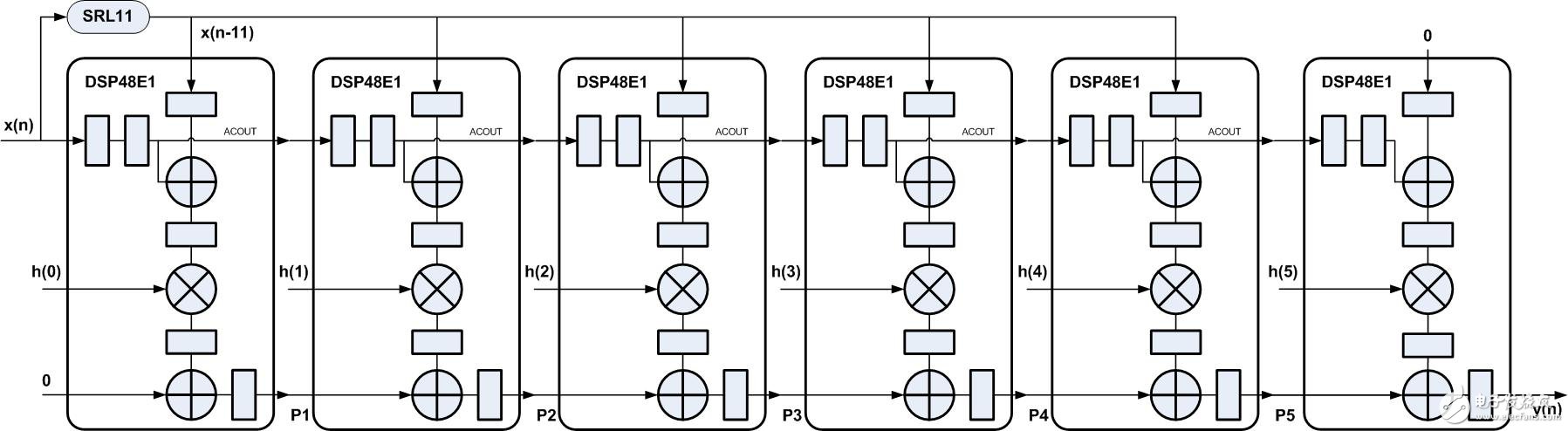
　　图3

　　而各节点P1、P2、P3、P4、P5和y（n）的表达式如下

　　P1=x（n-5）h（0） + x（n-15）h（0）

　　P2=（ P1 + （x（n-6）h（1） + x（n-14）h（1）） ）Z-1=x（n-6）h（0） + x（n-16）h（0） + x（n-7）h（1） + x（n-15）h（1）

　　P3=（ P2 + （x（n-8）h（2） + x（n-14）h（2）） ）Z-1=x（n-7）h（0） + x（n-17）h（0） + x（n-8）h（1） + x（n-16）h（1） + x（n-9）h（2） + x（n-15）h（2）

　　P4=（ P3 + （x（n-10）h（3） + x（n-14）h（3）） ）Z-1=x（n-8）h（0） + x（n-18）h（0） + x（n-9）h（1） + x（n-17）h（1） + x（n-10）h（2） + x（n-16）h（2） + x（n-11）h（3） + x（n-15）h（3）

　　P5=（ P4 + （x（n-12）h（4） + x（n-14）h（4）） ）Z-1=x（n-9）h（0） + x（n-19）h（0） + x（n-10）h（1） + x（n-18）h（1） + x（n-11）h（2） + x（n-17）h（2） + x（n-12）h（3） + x（n-16）h（3） + x（n-13）h（4） + x（n-15）h（4）

　　y（n）=（P5 + x（n-14）h（5））Z-1= x（n-10）h（0） + x（n-20）h（0） + x（n-11）h（1） + x（n-19）h（1） + x（n-12）h（2） + x（n-18）h（2） + x（n-13）h（3） + x（n-17）h（3） + x（n-14）h（4） + x（n-16）h（4） + x（n-15）h（5）

　　因抽头系数对称，由h（0）=h（10），h（1）=h（9），h（2）=h（8），h（3）=h（7），h（4）=h（6）可得

　　y（n）= x（n-10）h（0） + x（n-11）h（1） + x（n-12）h（2） + x（n-13）h（3） + x（n-14）h（4） + x（n-15）h（5） + x（n-16）h（6） + x（n-17）h（7） + x（n-18）h（8） + x（n-19）h（9） + x（n-20）h（10）

　　验证得到y（n）=yt（n-10），比普通脉动结构延时小，但是相比于其他结构的FIR滤波器延时还是较大的。

　　编写了相关代码，综合结果如下：

　　Number of Slice Registers： 84

　　Number of Slice LUTs： 99

　　Number of DSP48E1s： 6

　　Minimum period： 3.256ns{1} （Maximum frequency： 307.125MHz）

　　在DSP in FPGA： FIR滤波器设计（一）、（二）中分别讲解了直接型、转置型和脉动型结构FIR滤波器的实现方法，这三种结构是FPGA实现中比较常用的方法，以下对这三种结构做一个比较：

　　（1） 直接型：方法简单易实现，但是使用加法树优化后增加了功耗

　　（2） 转置型：关键路径延时较小，时序易满足，但是输入数据扇出较大，不适用于阶数较高的滤波器实现

　　（3） 脉动型：适用于高速数据处理，但是延时相比于其它结构较大