

半导体工艺之生产力和工艺良率
描述
工艺周期时间
晶圆实际被加工的时间可以以天为单位来衡量。但由于在工艺站点的排队以及由于工艺问题导致的临时减速,晶圆通常在制造区域停留数周。晶圆等待的时间越长,增加了污染的机会,这会降低晶圆分选良率。向准时制制造的转变(见后面章节)是提高良率和降低与增加的在线库存相关的制造成本的一次尝试。
晶圆分选良率公式
能够准确理解和预测晶圆分选良率对于一个盈利且可靠的芯片供应商的运营至关重要。多年来,已经开发了许多模型,这些模型将工艺、缺陷密度和芯片尺寸参数与晶圆分选良率联系起来。
下图展示了五种良率模型公式。每一种都将不同的参数与晶圆分选良率联系起来。随着芯片尺寸的增大,工艺步骤数量的增加,特征尺寸的减小,对更小缺陷尺寸的敏感性增加,更多的背景缺陷变成了致命缺陷。

指数模型
指数关系(下图所示)或泊松模型是最简单且最早开发的良率模型之一。它适用于单个工艺步骤,并假设晶圆上的缺陷(D0)随机分布。对于多步骤分析,使用等于工艺步骤数量的因子(n)(见下图)。这个模型通常用于包含超过300个裸片和低密度MSI电路的产品。更小的裸片尺寸由西德斯模型预测。
指数、泊松和西德斯模型都展示了裸片面积、缺陷密度和晶圆分选良率之间的主要关系。在这些模型中,e是一个常数,值为2.718。
B.T.墨菲提出了一个使用更复杂缺陷分布的模型。玻色-爱因斯坦模型增加了工艺步骤数量(n),而在负二项式模型中,有一个簇因子。它考虑了倾向于在晶圆表面上“聚集”的缺陷分布,而不仅仅是表现出随机分布。被SIA在ITRS中采纳,簇因子被赋予值为2。
在大多数良率模型中,处理步骤的因子(n)实际上是图案化步骤的数量。经验证明,图案化步骤产生最多的点缺陷,因此直接关系到分选良率。
没有两个复杂电路具有可比的设计或工艺。工艺在公司与公司之间不同,基本背景缺陷密度也是如此。这些因素使得开发一个准确的通用良率模型变得困难。大多数芯片公司都开发了自己的模型,这些模型反映了他们的特定制造工艺和产品设计。所有模型都是基于缺陷驱动的。也就是说,它们假设所有的制造工艺都在控制之下,缺陷水平是内置于工艺中的。它们不包括主要的工艺问题,例如污染的工艺气体罐。
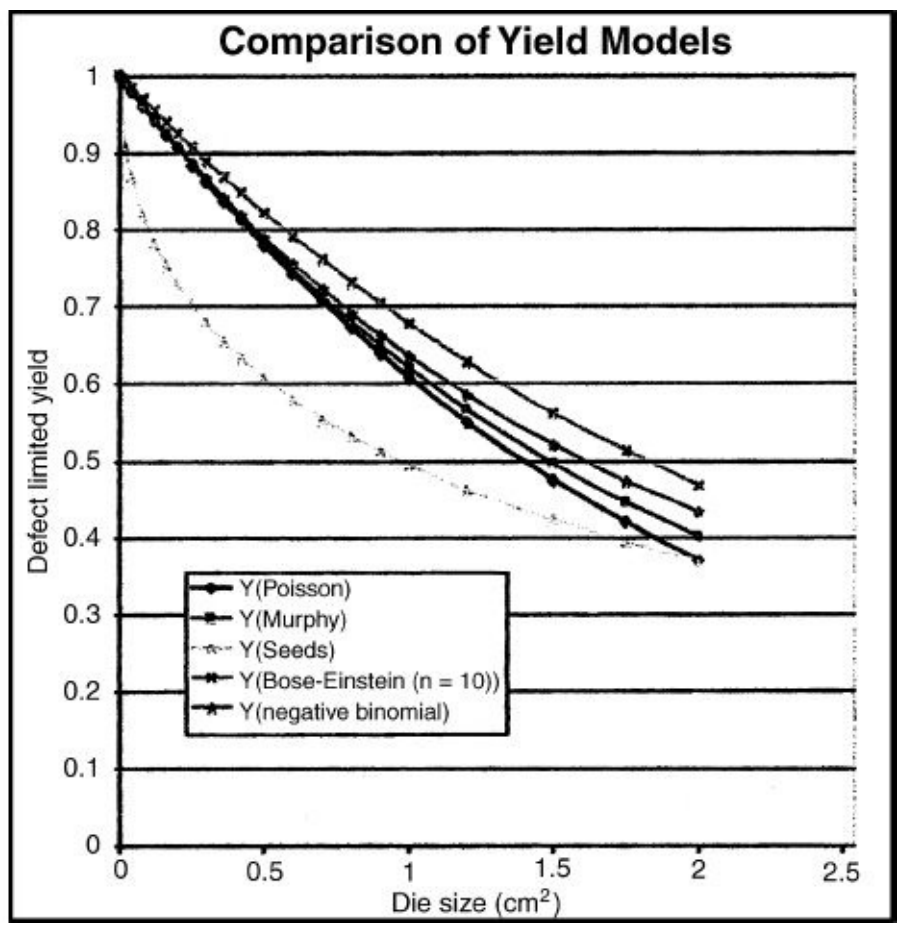
在所有模型中使用的缺陷密度与通过光学检查晶圆表面确定的缺陷密度不同。在良率模型中显示的缺陷密度是全面的;它包括污染物和表面以及晶体缺陷。此外,它只预测那些破坏裸片的缺陷:“致命缺陷”。落在芯片非关键区域的缺陷不包括在模型中,两个或更多的缺陷落在同一个敏感区域的情况也不包括。
-
半导体光刻蚀工艺2021-02-05 6994
-
半导体工艺几种工艺制程介绍2020-12-10 11153
-
单片机芯片生产工艺对单片机芯片良率的影响2020-07-05 3191
-
SPC在半导体在半导体晶圆厂的实际应用2018-08-29 4379
-
如何保证半导体良率2018-05-15 4520
-
常见的射频半导体工艺,你知道几种?2016-09-15 7043
-
半导体器件与工艺2012-08-20 45651
-
[课件]半导体工艺2012-02-26 23843
-
半导体工艺讲座2009-11-18 94497
-
有关半导体工艺的问题2009-09-16 5706
全部0条评论

快来发表一下你的评论吧 !

