

rlc串联谐振电路的主要特点 RLC串联谐振电路图
描述
RLC串联谐振电路是电路分析中的一个重要概念,它由电阻(R)、电感(L)和电容(C)依次串联连接而成。这种电路在特定频率下会表现出独特的性质,使得它在许多电子设备和系统中得到广泛应用。
一、谐振现象与谐振条件
1. 谐振现象
在RLC串联电路中,当外加交流电压的频率达到某一特定值时,电路中的电流、电压和阻抗会呈现出一系列特殊的现象,这种现象被称为谐振。谐振时,电路中的能量在电感、电容和电阻之间不断交换,但总体上保持不变,形成稳定的振荡状态。
2. 谐振条件
RLC串联电路发生谐振的条件是电路中的感抗(XL)与容抗(XC)相等且方向相反,即XL = XC。此时,电路的总阻抗最小,且为纯电阻性。谐振频率f0可以通过公式f0 = 1/(2π√LC)计算得出,其中L为电感值,C为电容值。
RLC串联谐振电路图
RLC 并联谐振电路如下图所示: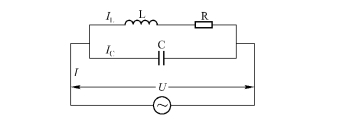
电阻 R、 电感 L 和电容 C 组成并联电路。 它的总阻抗 Z、 电流 I 与电压 U 的相位差分别为:

由上式可以描绘出总电流及总电阻随频率变化的关系曲线:

图中的极大值对应于的状态, 这时 Z 最大, I 最小, φ = 0, 电路呈纯阻性,这一状态被称为并联谐振, 其谐振频率为

f0 为RLC串联谐振电路的谐振频率, 当(CR平方 ) / L<<1 而可略去时, f = f0 。
和串联谐振电路类似, 电路的品质因数 Q 越大, 电路的频率选择性越好。
在谐振时, 两分支电路与电流 IL 和 IC 近似相等, 且等于总电流 I 的 Q 倍, 故并联谐振也被称为电流谐振。

图1 RLC串联谐振电路
根据RLC谐振电路(四)——阻抗与导纳的分析,图1所示电路的阻抗 Z =R+j(ωL-1/ωC)=| **Z** |ㄥφz,当ωL=1/ωC,也就是感抗的大小与容抗的大小相等时,因为感抗与容抗的相位相差180°——呈反相关系,所以电路的电抗X=0。此时电路中的阻抗**Z**最小,并且呈纯阻性,即:Z0=R。
由ωL=1/ωC解出ω0=1/√(LC)**(公式1)**,我们称ω0为电路的谐振频率。后续将谐振状态下的物理量都加下角标0加以区别,比如:ω0(f0)为电路的谐振频率,***I0***为电路谐振时的电流。
当电路进入谐振状态后,电路的阻抗最小,电流最大, I0 = Us /Z0= Us /R (公式2) ,由此可见,谐振时电路的电流I与激励源Us相位相同(同相),此时电阻上的电压UR = Us 。我们按图2搭建仿真电路与实际电路。

图2 RLC串联谐振电路及仿真波形
将图2电路中的L=10mH,C=0.1μF代入公式1,计算得:f0=ω0/2π=5.0kHz。因此当输入信号的频率为5.0kHz时,从仿真结果上看:电阻R上的信号波形与输入信号波形基本重合在一起,这说明***U******R***与***Us***的大小、相位都相同。
按照图2在CALK-1000电路分析实验套件的HA-MB03A电路分析实验板上搭建实际电路,当使用HPI-1000多功能口袋仪器A01信号源产生一个5Vp-p,频率为5kHz的正弦波作为输入信号时,从示波器上能看到图3所示实际波形。

图3 RLC串联谐振电路实际波形
图3中黄色的是输入信号 Us ,绿色的是电阻R上的信号UR ,谐振时实际电路中UR比Us小一些,主要是因为实际电路中的电感不是理想电感,存在一定的内阻,分去了输入信号Us的一部分电压。
以上分析了电路进入谐振状态后电阻上的电压信号UR与输入信号Us的关系,那电路没有进入谐振状态时,它们的关系又是什么样呢?请看图4。

图4a 利用波特图仪测量UR与Us信号的幅频、相频关系

图4b UR与Us信号的幅频关系(红色)、相频关系(蓝色)
借助Multisim软件中的波特图仪绘制出当输入信号频率0~20kHz区间变化时,电阻上的电压信号UR与输入信号Us的幅频关系与相频关系曲线。因为电路中的电流 I =UR /R,而根据公式2: I0 = Us /R,所以 I / I0 =UR / Us(公式3) 。这说明图4b所示的曲线也就是 I / I0 -ω(f)幅频关系与相频关系曲线,这条曲线称为谐振曲线,有时候也用 I / I0 -ω/ω0表示,即横轴与纵轴都做归一化处理。
二、主要特点
1. 阻抗特性
(1) 阻抗最小 :在谐振频率处,电路的总阻抗达到最小值,且为纯电阻性。这是因为此时感抗与容抗相互抵消,电路中只剩下电阻成分。
(2) 阻抗随频率变化 :在谐振频率两侧,电路的阻抗逐渐增大。低于谐振频率时,感抗大于容抗,电路呈感性;高于谐振频率时,容抗大于感抗,电路呈容性。
2. 电流与电压关系
(1) 电流电压同相位 :在谐振状态下,电路中的电流与电压同相位,即它们之间没有相位差。这意味着在谐振时,电路中的能量转换效率最高。
(2) 电流电压幅值关系 :谐振时,电路中的电流达到最大值,而电压也达到一个较高的水平。这是因为此时电路的阻抗最小,使得在相同电压下,电流能够达到最大。
3. 频率选择性
RLC串联谐振电路对频率具有高度的选择性。在谐振频率附近,电路对输入信号的响应最大;而在其他频率下,电路的响应则相对较小。这种频率选择性使得RLC串联谐振电路在信号处理、滤波和通信等领域具有广泛的应用。
4. 能量转换与储存
在谐振状态下,电路中的能量在电感、电容和电阻之间不断交换。电感储存磁场能量,电容储存电场能量,而电阻则消耗能量。这种能量交换和储存的过程是谐振现象的重要特征之一。
5. 品质因数(Q值)
品质因数Q是衡量RLC串联谐振电路性能的重要指标。它表示电路在谐振状态下储存的能量与每个周期内消耗的能量之比。Q值越大,表示电路的能量储存能力越强,谐振现象越明显。Q值的计算公式为Q = ω0L/R,其中ω0为谐振角频率,L为电感值,R为电阻值。
三、应用实例
1. 滤波器
RLC串联谐振电路可以作为滤波器使用,用于滤除特定频率的信号。通过调整电路中的电感、电容和电阻值,可以改变谐振频率和带宽,从而实现对不同频率信号的滤波效果。
2. 振荡器
在电子振荡器中,RLC串联谐振电路是产生稳定振荡信号的关键部分。通过合理的电路设计和参数调整,可以使得电路在谐振频率下产生稳定的正弦波信号。
3. 无线电接收与发射
在无线电通信中,RLC串联谐振电路被广泛应用于接收和发射电路中。在接收电路中,它用于选择并放大特定频率的信号;在发射电路中,它用于产生并调制高频信号。
四、结论
RLC串联谐振电路以其独特的阻抗特性、电流电压关系、频率选择性以及能量转换与储存能力等特点,在电子设备和系统中发挥着重要作用。通过对电路参数的合理设计和调整,可以实现对电路性能的精确控制和优化,从而满足不同应用场景的需求。未来,随着电子技术的不断发展和创新,RLC串联谐振电路的应用领域将会更加广泛和深入。
-
rlc串联谐振电路频率特性的特点2024-07-15 4750
-
如何判断rlc串联电路达到谐振状态2024-03-09 6107
-
rlc串联电路发生谐振的条件是什么2024-03-08 6805
-
RLC电路发生串联谐振的条件是什么?有哪些特点?2023-12-20 4325
-
rlc串联谐振电路的主要特点2023-12-14 7601
-
怎么判断RLC串联电路是否达到谐振状态?2023-10-11 7520
-
具体分析RLC谐振电路2023-06-08 30872
-
RLC串联谐振电路实验方法2020-09-22 5829
-
串联RLC电路的谐振2019-08-20 4720
-
rlc串联谐振电路图和原理2019-05-08 4608
-
RLC串联谐振电路的研究2012-08-16 4941
-
RLC串联电路谐振特性的Multisim仿真2012-01-31 2591
-
RLC串联电路谐振特性的实验研究2010-03-30 1239
-
rlc串联谐振电路图以及原理详解2007-12-03 24126
全部0条评论

快来发表一下你的评论吧 !

