

运放减法电路微分方程怎么求
描述
运放减法电路是模拟电路中的一种基本电路,广泛应用于信号处理、数据转换、滤波器等领域。在运放减法电路中,两个输入信号经过运算放大器(Op-Amp)进行减法运算,得到输出信号。本文将详细介绍运放减法电路的微分方程求解方法,包括电路原理、数学模型、求解步骤和实际应用。
- 运放减法电路原理
运放减法电路由一个运算放大器、两个输入电阻、一个反馈电阻和一个输出电阻组成。其基本电路结构如下图所示: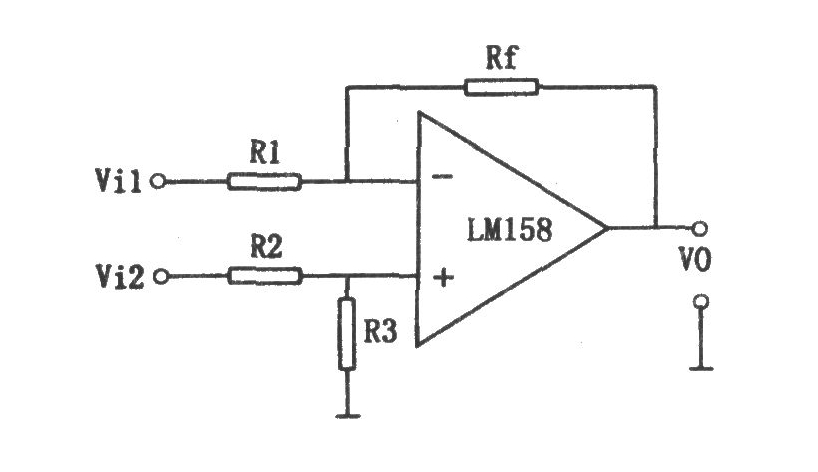
其中,Vin1和Vin2分别为输入信号,Vout为输出信号,R1和R2分别为输入电阻,Rf为反馈电阻。
运放减法电路的工作原理是:输入信号Vin1和Vin2分别通过输入电阻R1和R2输入到运算放大器的正负输入端,经过运算放大器的放大作用,得到差分信号Vdiff,然后通过反馈电阻Rf反馈到运算放大器的反相输入端,最终得到输出信号Vout。
- 运放减法电路数学模型
为了求解运放减法电路的微分方程,我们需要建立电路的数学模型。首先,我们假设运算放大器是一个理想运算放大器,具有以下特性:
- 增益无穷大:A = ∞
- 输入阻抗无穷大:Zin = ∞
- 输出阻抗为零:Zout = 0
根据理想运算放大器的特性,我们可以列出以下方程:
- Vp = Vn(虚短路)
- Ip = 0(虚断路)
其中,Vp和Vn分别为运算放大器的正负输入端电压,Ip为运算放大器的输入电流。
接下来,我们根据基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)列出电路的方程:
- Vout = Vp - Vn
- Vin1 = Vp - Vx1 * R1
- Vin2 = Vn - Vx2 * R2
- Vout = Vx1 - Vx2 * Rf
其中,Vx1和Vx2分别为输入电阻R1和R2上的电压。
将方程1)、2)、3)和4)联立,我们可以得到运放减法电路的微分方程:
C * dVout/dt = -(R1 * Vin1 + R2 * Vin2) * dVout/dt + Rf * (Vin1 - Vin2)
其中,C为电路的寄生电容。
- 微分方程求解步骤
求解运放减法电路的微分方程,我们可以采用以下步骤:
- 确定电路参数:根据电路设计,确定输入电阻R1、R2和反馈电阻Rf的值。
- 确定输入信号:根据实际应用,确定输入信号Vin1和Vin2的形式,例如正弦波、方波等。
- 建立微分方程:根据电路原理和数学模型,建立运放减法电路的微分方程。
- 求解微分方程:根据微分方程的形式,选择合适的求解方法,例如分离变量法、拉普拉斯变换法等。
- 分析输出信号:根据求解得到的输出信号Vout,分析其波形、频率、幅值等特性。
- 验证电路性能:通过实验或仿真,验证求解得到的输出信号与实际电路的输出信号是否一致。
- 实际应用
运放减法电路在实际应用中具有广泛的应用,例如:
- 信号处理:用于信号的加减、放大、衰减等操作。
- 数据转换:用于模拟信号与数字信号之间的转换,例如模数转换器(ADC)中的采样保持电路。
- 滤波器:用于滤除信号中的噪声或特定频率成分,例如低通滤波器、高通滤波器等。
- 传感器信号调理:用于传感器信号的放大、线性化、温度补偿等处理。
- 电源管理:用于电源电路中的电压调节、电流检测等操作。
- 结论
本文详细介绍了运放减法电路的微分方程求解方法,包括电路原理、数学模型、求解步骤和实际应用。通过求解微分方程,我们可以更好地理解运放减法电路的工作原理和性能特性,为电路设计和应用提供理论依据。
-
微分方程经典求解法2009-09-10 4328
-
Matlab偏微分方程工具箱应用说明2009-09-22 5892
-
Matlab求解微分方程(ODEs/PDEs)2011-07-08 8425
-
微分方程组求解2013-02-26 1815
-
请问微分方程如何转化成模拟电路2018-04-04 2570
-
一般RL串联电路的微分方程计算2019-01-08 15353
-
如何列写控制系统微分方程? 列写控制系统微分方程注意事项有哪些?2021-10-25 1739
-
【全美经典】微分方程 第二版2008-08-08 817
-
常微分方程的MAtLAB解法2009-01-08 606
-
含一般时延的高阶泛函微分方程的周期解2009-02-28 627
-
常微分方程复习,常微分方程pdf2009-04-23 994
-
导热微分方程式视频教程2009-07-05 728
-
微分方程式的建立与求解2009-09-30 2242
-
一类高阶非线性微分方程的解法2010-03-03 982
-
Matlab的微分、积分和微分方程2008-10-17 4816
全部0条评论

快来发表一下你的评论吧 !

